Alcune osservazioni sulla forma logica

 

Ludwig Wittgenstein

Alcune osservazioni sulla forma logica

Traduzione di Filippo Villaggi

 

Questa traduzione è stata condotta sul testo di Ludwig Wittgenstein, "Some Remarks on Logical Form", Proceedings of the Aristotelian Society, Supplementary Volume 9, Jul. 1929, pp. 162-171. Il testo originale è nel pubblico dominio in tutti i paesi dove i diritti di proprietà intellettuale scadono 70 anni o meno dopo la morte dell'autore. Questa traduzione è pubblicata secondo i termini della licenza Creative Commons Attribuzione – Condividi allo stesso modo.

Ludwig Wittgenstein

Alcune osservazioni sulla forma logica

Ogni proposizione ha un contenuto e una forma. Otteniamo l’immagine della forma pura se facciamo astrazione dal significato delle singole parole, o simboli (nella misura in cui hanno significati indipendenti); vale a dire, se sostituiamo variabili alle costanti della proposizione. Le regole della sintassi che valevano per le costanti devono valere anche per le variabili. Per sintassi, in questo senso generale della parola, io intendo le regole che ci dicono quali sono quelle sole connessioni all’interno delle quali una parola ha significato, escludendo così le formazioni insensate. La sintassi del linguaggio ordinario, com’è risaputo, non è del tutto adeguata a questo scopo. Essa non previene in tutti i casi la costruzione di pseudo-proposizioni insensate (costruzioni quali “il rosso è più alto del verde” o “la Realtà, benché sia un in sé, deve poter diventare altrettanto bene un per me”, etc.).

Se proviamo ad analizzare una qualsiasi proposizione data, troveremo in generale che essa è una somma logica, un prodotto logico o un’altra funzione di verità di proposizioni più semplici. Ma la nostra analisi, se portata avanti a sufficienza, deve arrivare al punto in cui raggiunge forme proposizionali che non sono esse stesse composte di forme proposizionali più semplici. Prima o poi dobbiamo raggiungere la connessione ultima dei termini, la connessione immediata che non può essere spezzata senza sopprimere la forma proposizionale come tale. Le proposizioni che presentano questa connessione ultima dei termini io le chiamo, seguendo B. Russell, proposizioni atomiche. Queste, pertanto, sono il nocciolo di ogni proposizione, sono queste a contenere la materia prima, e tutto il resto non è che uno sviluppo di questa materia prima. È ad esse che noi dobbiamo guardare se siamo alla ricerca del contenuto delle proposizioni. È compito della teoria della conoscenza trovarle e comprendere il modo in cui sono costruite a partire dalle parole o simboli. Questo compito è molto difficile e la Filosofia ha a malapena iniziato a misurarcisi sotto alcuni rispetti. Di quale metodo disponiamo per affrontarlo? L’idea è di esprimere in un simbolismo appropriato quanto nel linguaggio ordinario conduce a fraintendimenti senza fine. Detto altrimenti, dove il linguaggio ordinario nasconde la struttura logica, dove consente la formazione di pseudo-proposizioni, dove impiega un singolo termine in un’infinità di significati differenti, dobbiamo rimpiazzarlo con un simbolismo che dia una chiara immagine della struttura logica, escluda le pseudo-proposizioni e impieghi i termini in maniera inequivocabile. Ora, noi possiamo sostituire un simbolismo chiaro a quello impreciso solamente ispezionando i fenomeni che vogliamo descrivere, cioè cercando di comprendere la loro molteplicità logica. In altre parole, possiamo pervenire a un’analisi corretta soltanto per mezzo di quella che si può chiamare un’indagine logica dei fenomeni stessi, vale a dire, in un certo senso, a posteriori e senza congetturare nulla sulle loro possibilità a priori. Si è spesso tentati di chiedersi, da un punto di vista a priori: Quali possono essere, tutto considerato, le sole forme delle proposizioni atomiche?, e di rispondere, ad esempio: Proposizioni soggetto-predicato e proposizioni relazionali a due o più posti e poi, forse, proposizioni che mettono in relazione tra loro predicati e relazioni, e così via. Ma questo, io credo, è un mero gioco di parole. Una forma atomica non si può prevedere. E sarebbe sorprendente se i fenomeni reali non avessero nulla di più da insegnarci sulla propria struttura. A simili congetture circa la struttura delle proposizioni atomiche noi siamo condotti dal nostro linguaggio ordinario, che impiega la forma soggetto-predicato e la forma relazionale. Ma in ciò il nostro linguaggio è fuorviante: cercherò di spiegarlo con una similitudine. Immaginiamo due piani paralleli, I e II. Sul piano I sono disegnate delle figure, diciamo ellissi e rettangoli di differenti dimensioni e forme, e il nostro compito è di riprodurre di queste figure sul piano II. Possiamo immaginarci due modi, tra gli altri, di fare ciò. Possiamo, primo, stabilire una legge di proiezione – poniamo, quella della proiezione ortogonale o un’altra qualsiasi – e poi procedere a proiettare le figure da I a II seguendo questa legge. Oppure, secondo, potremmo procedere così: Stabiliamo la regola che ogni ellisse sul piano I deve apparire come cerchio sul piano II, e ogni rettangolo come un quadrato su II. Questa maniera di rappresentazione può tornarci utile se per qualche ragione preferiamo tracciare solo cerchi e quadrati sul piano II. Naturalmente, da queste raffigurazioni non si può inferire immediatamente la forma esatta delle figure originali sul piano I. Possiamo soltanto dedurre da esse che l’originale era un’ellisse o un rettangolo. Per risalire alla forma determinata dell’originale in un dato caso, dovremmo conoscere il metodo specifico con il quale, per esempio, un’ellisse in particolare viene proiettata nel cerchio che ho davanti. Il caso del linguaggio ordinario è del tutto analogo. Se i fatti della realtà sono le ellissi e i rettangoli sul piano I, la forma soggetto-predicato e quella relazionale corrispondono ai cerchi e ai quadrati sul piano II. Queste forme sono le norme del nostro peculiare linguaggio, nel quale proiettiamo un’infinità di forme logiche differenti in un’infinità di modi differenti. E proprio per questa ragione non possiamo trarre conclusioni che non siano assai vaghe dall’impiego di queste norme circa la forma logica reale dei fenomeni descritti. Forme come “questo articolo è noioso”, “il tempo è bello”, “sono pigro”, che non hanno nulla in comune tra di loro, si presentano come proposizioni soggetto-predicato, cioè, apparentemente, come proposizioni della stessa forma.

Se ora ci accingiamo a un’analisi vera e propria, scopriamo forme logiche che hanno una somiglianza assai limitata con le regole del linguaggio ordinario. Ci imbattiamo nelle forme dello spazio e del tempo con l’intera varietà degli oggetti spaziali e temporali, come colori, suoni, etc., etc., con le loro gradazioni, transizioni continue e combinazioni in svariate proposizioni: noi non possiamo cogliere tutto questo con i nostri comuni mezzi d’espressione. E qui vorrei fare la mia prima osservazione circostanziata sull’analisi logica dei fenomeni reali: cioè che, per rappresentarli, dobbiamo far entrare i numeri (razionali e irrazionali) nella struttura delle proposizioni atomiche stesse. Lo illustrerò con un esempio. Si immagini un sistema di assi ortogonali, per così dire un reticolo, disegnato nel nostro campo visivo e una scala fissata arbitrariamente. È chiaro che possiamo in tal modo descrivere la forma e la posizione di ogni macchia di colore nel nostro campo visivo per mezzo di asserzioni contenenti numeri il cui significato è relativo al sistema di coordinate e all’unità di misura scelta. Di nuovo, è evidente che questa descrizione avrà la giusta molteplicità logica e che un’altra descrizione la cui molteplicità è minore non andrà bene. Un semplice esempio è dato dalla rappresentazione di una macchia P per mezzo dell’espressione “[6-9, 3-8]” e di una proposizione

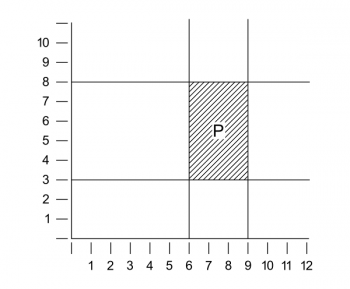
su di essa, per esempio “P è rossa”, per mezzo del simbolo “[6-9, 3-8] R”, dove “R” è un termine non ancora analizzato (“6-9” e “3-8” stanno per l’intervallo continuo tra i rispettivi numeri). Il sistema di coordinate qui è parte del modo di espressione; è parte del metodo di proiezione attraverso il quale la realtà viene proiettata nel nostro simbolismo. La relazione di una macchia che giace in mezzo ad altre due può essere espressa in maniera simile usando variabili apparenti. Non c’è bisogno di precisare che quest’analisi non pretende affatto di essere completa. In essa non ho fatto menzione del tempo e l’adozione di uno spazio bidimensionale non è giustificata nemmeno nel caso della visione monoculare. Desidero soltanto suggerire la direzione nella quale, a mio avviso, va cercata l’analisi dei fenomeni visivi e che in questa analisi incontriamo forme logiche affatto differenti da quelle che il linguaggio ordinario ci induce ad aspettarci. La ricorrenza di numeri nelle forme delle proposizioni atomiche non è, dal mio punto di vista, soltanto una caratteristica di un simbolismo speciale, ma un tratto essenziale e, perciò, imprescindibile della rappresentazione. E i numeri dovranno entrare in queste forme ogniqualvolta – come diremmo nel linguaggio ordinario – avremo a che fare con proprietà che ammettono una gradazione, cioè proprietà come la lunghezza di un intervallo, l’altezza di un suono, la luminosità o la rossezza di una sfumatura di colore, etc. È caratteristico di queste proprietà che un grado di esse escluda ogni altro. Una sfumatura di colore non può avere simultaneamente due differenti gradi di luminosità o rossezza, un suono due differenti intensità, etc. E il punto rilevante, qui, è che queste osservazioni non si riferiscono a un’esperienza, ma sono in un certo senso tautologie. Ognuno di noi lo sa nella vita quotidiana. Se alla domanda: “Che temperatura c’è fuori?”, noi rispondessimo: “Venticinque gradi”, e ora ci venisse chiesto di nuovo: “Ci sono trenta gradi?”, dovremmo rispondere: “Ti ho detto che ci sono venticinque gradi”. Noi consideriamo l’attestazione di un grado (di temperatura, per esempio) una descrizione completa, che non richiede integrazioni. Così, quando ci viene chiesto, diciamo che ore sono, non anche che ore non sono.

Uno potrebbe pensare – e io stesso lo pensavo non molto tempo fa – che un’asserzione che esprime il grado di una qualità possa essere analizzata come un prodotto logico di singole asserzioni di quantità e di un’asserzione aggiuntiva di complemento. Così potrei descrivere il contenuto della mia tasca dicendo: “Contiene un penny, uno scellino, due chiavi, e nient’altro”. Questo “e nient’altro” è l’asserzione supplementare che completa la descrizione. Ma ciò, come analisi di un’asserzione di grado, non va bene. Infatti, se noi chiamiamo l’unità di misura, poniamo, della luminosità “b” e se E(b) è l’asserzione che l’entità E possiede quella luminosità, allora la proposizione E(2b), che dice che E ha due gradi di luminosità, dovrebbe essere analizzabile come il prodotto logico E(b) ˄ E(b), ma questo è uguale a E(b). Se, d’altra parte, proviamo a distinguere tra le unità e scriviamo dunque E(2b) = E(b') ˄ E(b"), assumiamo due differenti misure della luminosità e, di conseguenza, se un’entità possiede una sola unità, può sorgere la questione di quale delle due – b' o b" – essa sia; il che è ovviamente un’assurdità.

Io ritengo che l’asserzione che attribuisce un grado a una qualità non possa essere ulteriormente analizzata e che, inoltre, la relazione di differenza di grado è una relazione interna e che pertanto essa è rappresentata da una relazione interna tra le asserzioni che attribuiscono i differenti gradi. In altri termini, l’asserzione atomica deve avere la stessa molteplicità del grado che esso attribuisce; dal che risulta che i numeri debbono entrare nella forma delle proposizioni atomiche. La mutua esclusione delle asserzioni di grado non analizzabili confuta un’opinione che fu da me resa pubblica diversi anni fa e che implicava che le proposizioni atomiche non possono escludersi a vicenda. Qui dico deliberatamente “escludere” e non “contraddire”, perché c’è una differenza tra queste due nozioni e le proposizioni atomiche, per quanto non possano contraddirsi, possono escludersi reciprocamente. Cercherò di spiegarlo. Ci sono funzioni che possono dare come risultato una proposizione vera per un solo valore del loro argomento poiché – se mi è consentito esprimermi in questo modo – c’è posto al loro interno per uno solo di essi. Si prenda, ad esempio, una proposizione che asserisce l’esistenza di un colore R in un dato momento T in un dato punto P del nostro campo visivo. Scriverò questa proposizione “R P T” e farò astrazione per il momento da ogni considerazione su come un asserto del genere debba essere ulteriormente analizzato. “B P T”, quindi, dice che il colore B è nel punto P nel momento T e qui risulterà chiaro alla maggior parte di noi, e a tutti noi nella nostra vita quotidiana, che “R P T ˄ B P T” è una specie di contraddizione (e non soltanto una proposizione falsa). Ora, se le asserzioni di grado fossero analizzabili – come io pensavo – potremmo spiegare questa contraddizione dicendo che il colore R contiene tutti i gradi di R e nessuno di B e che il colore B contiene tutti i gradi di B e nessuno di R. Ma da quanto detto segue che nessuna analisi può sopprimere asserzioni di grado. Come avviene allora la mutua esclusione di R P T e B P T? Io ritengo che consista nel fatto che R P T così come B P T sono in un certo senso complete. Ciò che corrisponde nella realtà alla funzione “( ) P T” lascia spazio soltanto per una entità – nello stesso senso, in effetti, in cui diciamo che su una sedia c’è spazio soltanto per una persona. Il nostro simbolismo, che ci permette di comporre il segno del prodotto logico di “R P T” e “B P T”, non fornisce qui un’immagine corretta della realtà.

Ho detto altrove che una proposizione “raggiunge la realtà” e con ciò io intendevo che le forme delle entità sono contenute nella forma della proposizione che verte su quelle entità. Giacché l’enunciato, insieme al modo di proiezione che proietta la realtà nell’enunciato, determina la forma logica delle entità, proprio come nella nostra similitudine una figura sul piano II, insieme al suo modo di proiezione, determina la forma della figura sul piano I. Questa osservazione, credo, ci dà la chiave per la spiegazione della mutua esclusione di R P T e B P T. Infatti, se la proposizione contiene la forma di un’entità di cui parla, allora è possibile che due proposizioni collidano relativamente a questa stessa forma. Le proposizioni “Brown in questo momento è seduto su questa sedia” e “Jones in questo momento è seduto su questa sedia” cercano ognuna, per così dire, di mettere sulla sedia il proprio soggetto. Ma il prodotto logico di queste proposizioni li mette là entrambi simultaneamente e questo porta a una collisione, a una mutua esclusione di questi soggetti. Come si presenta questa esclusione nel simbolismo? Possiamo scrivere il prodotto logico delle due proposizioni p e q nel modo seguente:

p	q
V	V	V
V	F	F
F	V	F
F	F	F

Che cosa succede se queste due proposizioni sono R P T e B P T? In questo caso la riga superiore “V V V” deve scomparire, perché essa rappresenta una combinazione impossibile. Le possibilità effettive qui sono

R P T	B P T
V	F
F	V
F	F

Ciò vuol dire che non c’è prodotto logico di R P T e B P T nel primo caso e qui risiede l’esclusione in quanto opposta alla contraddizione. La contraddizione, se esistesse, dovrebbe essere scritta così:

R P T	B P T
V	V	F
V	F	F
F	V	F
F	F	F

ma questo è un nonsenso, perché la riga superiore “V V F” conferisce alla proposizione una molteplicità logica maggiore di quella delle possibilità effettive. Ovviamente, è una mancanza della nostra notazione che essa non impedisca la formazione di tali costruzioni insensate; una notazione perfetta dovrà escludere tali strutture per mezzo di regole della sintassi definite. Queste dovranno dirci che, nel caso di certi tipi di proposizioni atomiche descritte nei termini di determinate caratteristiche simboliche, alcune combinazioni del vero e del falso non devono essere ammesse. Tali regole, tuttavia, non possono essere stabilite finché non avremo davvero raggiunto l’analisi ultima dei fenomeni in questione. Questo obiettivo, come tutti sappiamo, non è stato ancora conseguito.