Notas Ditadas a G.E. Moore na Noruega: Difference between revisions
No edit summary |
No edit summary |
||
| Line 17: | Line 17: | ||
{{p right|Abril, 1914}} | {{p right|Abril, 1914}} | ||
Proposições assim chamadas lógicas ''mostram'' [as] propriedades lógicas da linguagem, e portanto, do Universo, mas nada ''dizem.'' [Cf. 6.12.] | Proposições assim chamadas lógicas ''mostram'' [as] propriedades lógicas da linguagem, e portanto, do Universo, mas nada ''dizem.'' <!-- [Cf. 6.12.] --> | ||
Isso significa que, por meramente olhar para elas, você consegue ''ver'' essas propriedades; enquanto que, em uma proposição adequada, você não consegue ver o que é verdade, apenas olhando para ela. [Cf. 6.113.] | Isso significa que, por meramente olhar para elas, você consegue ''ver'' essas propriedades; enquanto que, em uma proposição adequada, você não consegue ver o que é verdade, apenas olhando para ela. <!-- [Cf. 6.113.] --> | ||
É impossível ''dizer'' o que essas propriedades são, pois, para fazer isso,você precisaria de uma linguagem, que não possui as propriedades em questão, e é impossível que isso seja uma linguagem ''própria''. Impossível construir [uma] linguagem ilógica. | É impossível ''dizer'' o que essas propriedades são, pois, para fazer isso,você precisaria de uma linguagem, que não possui as propriedades em questão, e é impossível que isso seja uma linguagem ''própria''. Impossível construir [uma] linguagem ilógica. | ||
| Line 31: | Line 31: | ||
Como, geralmente, proposições lógicas mostram essas propriedades funciona assim: Nós damos uma certa descrição para uma espécie de símbolo; nós descobrimos que outros símbolos, combinados de certos modos, produzem um símbolo dessa descrição; e ''que'' elas mostram algo sobre esses símbolos. | Como, geralmente, proposições lógicas mostram essas propriedades funciona assim: Nós damos uma certa descrição para uma espécie de símbolo; nós descobrimos que outros símbolos, combinados de certos modos, produzem um símbolo dessa descrição; e ''que'' elas mostram algo sobre esses símbolos. | ||
Em regra, a descrição [fornecida] na Lógica ordinária é a descrição de uma tautologia; mas ''outras'' podem expor igualmente bem, e.g., uma contradição. [Cf. 6.1202.] | Em regra, a descrição [fornecida] na Lógica ordinária é a descrição de uma tautologia; mas ''outras'' podem expor igualmente bem, e.g., uma contradição. <!-- [Cf. 6.1202.] --> | ||
Toda proposição ''real mostra'' alguma coisa, além do que diz, sobre o Universo: ''pois'', se ela não tem sentido, não pode ser utilizada; e se tem sentido, ela espelha alguma propriedade lógica do Universo. | Toda proposição ''real mostra'' alguma coisa, além do que diz, sobre o Universo: ''pois'', se ela não tem sentido, não pode ser utilizada; e se tem sentido, ela espelha alguma propriedade lógica do Universo. | ||
E.g., considere ϕa, ϕa '''⊃''' ψa, ψa. Por meramente olhar esses três [símbolos], eu posso perceber que 3 se segue de 1 e 2; i.e. eu posso perceber o que é chamado de verdade de uma proposição lógica, isto é, d[a] proposição ϕa. ϕa '''⊃''' ψa : '''⊃''' : ψa. Mas isso ''não'' é uma proposição; pois, ao perceber que isso é uma tautologia, eu posso ver o que eu já vi ao olhar as três proposições: a diferença é que ''agora'' eu vejo que {{small caps|aquilo}} é uma tautologia. [Cf. 6.1221.]. | E.g., considere ϕa, ϕa '''⊃''' ψa, ψa. Por meramente olhar esses três [símbolos], eu posso perceber que 3 se segue de 1 e 2; i.e. eu posso perceber o que é chamado de verdade de uma proposição lógica, isto é, d[a] proposição ϕa. ϕa '''⊃''' ψa : '''⊃''' : ψa. Mas isso ''não'' é uma proposição; pois, ao perceber que isso é uma tautologia, eu posso ver o que eu já vi ao olhar as três proposições: a diferença é que ''agora'' eu vejo que {{small caps|aquilo}} é uma tautologia. <!-- [Cf. 6.1221.] -->. | ||
Nós queremos dizer que, para entender [o] dito acima, quais propriedades um símbolo deve ter, para que seja uma tautologia. | Nós queremos dizer que, para entender [o] dito acima, quais propriedades um símbolo deve ter, para que seja uma tautologia. | ||
| Line 45: | Line 45: | ||
Esse é o procedimento d[a] chamada Lógica ''antiga'': fornece proposições primitivas; chamadas regras de dedução; e então diz o que você tem aplicando as regras às proposições, é uma proposição ''lógica'' que você ''provou.'' A verdade é, ela diz algo sobre o tipo de proposição que você tem, viz. [''videlicet'' = isto é] que ela pode ser derivada dos primeiros símbolos por essas regras de combinação (= é uma tautologia). | Esse é o procedimento d[a] chamada Lógica ''antiga'': fornece proposições primitivas; chamadas regras de dedução; e então diz o que você tem aplicando as regras às proposições, é uma proposição ''lógica'' que você ''provou.'' A verdade é, ela diz algo sobre o tipo de proposição que você tem, viz. [''videlicet'' = isto é] que ela pode ser derivada dos primeiros símbolos por essas regras de combinação (= é uma tautologia). | ||
Assim, se dissermos que uma proposição ''lógica'' ''se segue'' logicamente de outra, isso quer dizer algo bem diferente de dizer que uma proposição ''real'' se segue logicamente de ''outra''. Pois a chamada ''prova'' de uma proposição lógica não prova sua ''verdade'' (proposições lógicas não são nem verdadeiras nem falsas) mas prova ''que'' é uma proposição lógica (= é uma tautologia). [Cf. 6.1264] | Assim, se dissermos que uma proposição ''lógica'' ''se segue'' logicamente de outra, isso quer dizer algo bem diferente de dizer que uma proposição ''real'' se segue logicamente de ''outra''. Pois a chamada ''prova'' de uma proposição lógica não prova sua ''verdade'' (proposições lógicas não são nem verdadeiras nem falsas) mas prova ''que'' é uma proposição lógica (= é uma tautologia). <!-- [Cf. 6.1264] --> | ||
Proposições lógicas são ''formas de prova'': elas ''mostram'' que uma ou mais proposições ''se seguem'' de uma (ou mais). [Cf. 6.1264] | Proposições lógicas são ''formas de prova'': elas ''mostram'' que uma ou mais proposições ''se seguem'' de uma (ou mais). <!-- [Cf. 6.1264] --> | ||
Proposições lógicas ''mostram'' algo, ''porque'' a linguagem na qual elas são expressadas pode ''dizer'' tudo o que pode ser ''dito''. | Proposições lógicas ''mostram'' algo, ''porque'' a linguagem na qual elas são expressadas pode ''dizer'' tudo o que pode ser ''dito''. | ||
| Line 89: | Line 89: | ||
{{p indent|(1) quer dizer: (∃x) . ϕx . x <nowiki>=</nowiki> a}} | {{p indent|(1) quer dizer: (∃x) . ϕx . x <nowiki>=</nowiki> a}} | ||
{{p indent|(2) quer dizer: (∃x, ψξ) . ϕA <nowiki>=</nowiki> ψx . ϕx.<ref>ξ é a marca de Frege de um ''Argumentstelle'' [posição do argumento], para mostrar que ψ é uma ''Funktionsbuchstabe'' [letra de função] [Edd.].</ref>}} | {{p indent|(2) quer dizer: (∃x, ψξ) . ϕA <nowiki>=</nowiki> ψx . ϕx.<!-- <ref>ξ é a marca de Frege de um ''Argumentstelle'' [posição do argumento], para mostrar que ψ é uma ''Funktionsbuchstabe'' [letra de função] [Edd.].</ref> -->}} | ||
''Uso de proposições lógicas''. Você pode ter uma tão complicada que você não consegue, ao olhar para ela, ver que é uma tautologia; mas você mostrou que pode ser derivada por determinas operações a partir de certas outras proposições de acordo com nossa regra para construir tautologias; e assim você está habilitado para ver que uma coisa se segue da outra, quando você não seria capaz de ver isso de outro modo. E.g., se nossa tautologia é d[a] forma p ⊃ q você pode ver que p se segue de p; e assim por diante. | ''Uso de proposições lógicas''. Você pode ter uma tão complicada que você não consegue, ao olhar para ela, ver que é uma tautologia; mas você mostrou que pode ser derivada por determinas operações a partir de certas outras proposições de acordo com nossa regra para construir tautologias; e assim você está habilitado para ver que uma coisa se segue da outra, quando você não seria capaz de ver isso de outro modo. E.g., se nossa tautologia é d[a] forma p ⊃ q você pode ver que p se segue de p; e assim por diante. | ||
| Line 101: | Line 101: | ||
Nós queremos explicar a relação das proposições com a realidade. | Nós queremos explicar a relação das proposições com a realidade. | ||
A relação é a seguinte: Seus simples têm significado = são nomes de simples; e suas relações tem uma relação bem diferente com relações; e esses dois fatos já estabelecem uma espécie de correspondência entre a proposição que contém esses, e apenas esses, e a realidade: i.e. se todos os simples de uma proposição são conhecidos, nós já sabemos que {{small caps|podemos}} descrever a realidade ao dizer que ela se ''comporta''<ref>Presumivelmente “verhält sich zu”, i.e. “está relacionado” [Edd.].</ref> de um certo modo para o todo da proposição. (Isso equivale dizer que nós podemos ''comparar'' realidade com proposição. No caso de duas linhas, nós podemos ''compará-las'' em relação ao seu comprimento sem nenhuma convenção: a comparação é automática. Mas no nosso caso a possibilidade da comparação depende das convenções pelas quais nós damos sentido aos nossos simples (nomes e relações). | A relação é a seguinte: Seus simples têm significado = são nomes de simples; e suas relações tem uma relação bem diferente com relações; e esses dois fatos já estabelecem uma espécie de correspondência entre a proposição que contém esses, e apenas esses, e a realidade: i.e. se todos os simples de uma proposição são conhecidos, nós já sabemos que {{small caps|podemos}} descrever a realidade ao dizer que ela se ''comporta''<!--<ref>Presumivelmente “verhält sich zu”, i.e. “está relacionado” [Edd.].</ref>--> de um certo modo para o todo da proposição. (Isso equivale dizer que nós podemos ''comparar'' realidade com proposição. No caso de duas linhas, nós podemos ''compará-las'' em relação ao seu comprimento sem nenhuma convenção: a comparação é automática. Mas no nosso caso a possibilidade da comparação depende das convenções pelas quais nós damos sentido aos nossos simples (nomes e relações). | ||
Apenas resta fixar o método de comparação ao dizer ''o quê'' sobre nossos simples é ''dizer'' o quê sobre a realidade. E.g., suponha que peguemos duas linhas de comprimentos diferentes: e dizemos que o fato de a menor ser de um comprimento que é quer dizer que a maior é do comprimento que ''ela'' é. Nós deveríamos então ter estabelecido uma convenção quanto ao sentido da menor, do tipo que vamos dar agora. | Apenas resta fixar o método de comparação ao dizer ''o quê'' sobre nossos simples é ''dizer'' o quê sobre a realidade. E.g., suponha que peguemos duas linhas de comprimentos diferentes: e dizemos que o fato de a menor ser de um comprimento que é quer dizer que a maior é do comprimento que ''ela'' é. Nós deveríamos então ter estabelecido uma convenção quanto ao sentido da menor, do tipo que vamos dar agora. | ||
| Line 121: | Line 121: | ||
''Proposições lógicas'', {{small caps|é claro}}, todas mostram algo diferente: todas elas mostram, ''do mesmo modo'', viz. pelo fato de que elas são tautologias, mas elas são diferentes tautologias e portanto cada uma mostra algo diferente. | ''Proposições lógicas'', {{small caps|é claro}}, todas mostram algo diferente: todas elas mostram, ''do mesmo modo'', viz. pelo fato de que elas são tautologias, mas elas são diferentes tautologias e portanto cada uma mostra algo diferente. | ||
O que é não-arbitrário sobre nossos símbolos não são eles, nem as regras que damos; mas o fato de que, tendo dadas certas regras, outras são fixadas = se seguem logicamente. [Cf. 3.342.] | O que é não-arbitrário sobre nossos símbolos não são eles, nem as regras que damos; mas o fato de que, tendo dadas certas regras, outras são fixadas = se seguem logicamente. <!-- [Cf. 3.342.] --> | ||
Assim, embora fosse possível interpretar a forma que tomamos como a forma de uma tautologia, como de uma contradição e vice versa, elas ''são'' diferentes na forma lógica porque, apesar da forma aparente dos símbolos ser a mesma, o que ''simboliza'' neles é diferente, e por isso o que se segue sobre os símbolos de uma interpretação vai ser diferente do que se segue de outra. Mas a diferença entre a e b ''não'' é uma forma lógica, de modo que nada vai se seguir dessa diferença sozinha quanto a interpretação de outros símbolos. Então, e.g., p.q., p ∨ q parecem símbolos da exata ''mesma'' forma lógica na notação ab. Ainda assim elas dizem algo inteiramente diferente; e, se você perguntar por quê, a resposta parece ser: Em um caso o esboço em cima tem o formato b, em outro o formato a. Enquanto que a interpretação de uma tautologia como uma tautologia é uma interpretação de uma ''forma lógica'', não o fornecimento de um significado para o rascunho de uma forma particular. O que importa é que a interpretação da forma do simbolismo deve ser fixada dando uma interpretação para suas ''propriedades lógicas'', e ''não'' dando interpretações para rascunhos particulares. | Assim, embora fosse possível interpretar a forma que tomamos como a forma de uma tautologia, como de uma contradição e vice versa, elas ''são'' diferentes na forma lógica porque, apesar da forma aparente dos símbolos ser a mesma, o que ''simboliza'' neles é diferente, e por isso o que se segue sobre os símbolos de uma interpretação vai ser diferente do que se segue de outra. Mas a diferença entre a e b ''não'' é uma forma lógica, de modo que nada vai se seguir dessa diferença sozinha quanto a interpretação de outros símbolos. Então, e.g., p.q., p ∨ q parecem símbolos da exata ''mesma'' forma lógica na notação ab. Ainda assim elas dizem algo inteiramente diferente; e, se você perguntar por quê, a resposta parece ser: Em um caso o esboço em cima tem o formato b, em outro o formato a. Enquanto que a interpretação de uma tautologia como uma tautologia é uma interpretação de uma ''forma lógica'', não o fornecimento de um significado para o rascunho de uma forma particular. O que importa é que a interpretação da forma do simbolismo deve ser fixada dando uma interpretação para suas ''propriedades lógicas'', e ''não'' dando interpretações para rascunhos particulares. | ||
| Line 155: | Line 155: | ||
{{p indent|p é falso <nowiki>=</nowiki> ~(p é verdadeiro) Def.}} | {{p indent|p é falso <nowiki>=</nowiki> ~(p é verdadeiro) Def.}} | ||
É muito importante que as aparentes relações lógicas ∨, ⊃, etc. precisem de colchetes, pontos, etc., i.e. ter “gamas”; que por si só mostra que eles não são relações. Esse fato tem sido menosprezado, porque é muito universal – a coisa mesma que deixa isso importante. [Cf. 5.461.] | É muito importante que as aparentes relações lógicas ∨, ⊃, etc. precisem de colchetes, pontos, etc., i.e. ter “gamas”; que por si só mostra que eles não são relações. Esse fato tem sido menosprezado, porque é muito universal – a coisa mesma que deixa isso importante. <!-- [Cf. 5.461.] --> | ||
Existem relações ''internas'' entre uma proposição e outra; mas uma proposição não pode ter com outra ''a'' relação interna que um ''nome'' tem com a proposição da qual seja constituinte e que deveria significar ao dizer que “ocorre” nela. Nesse sentido, uma proposição não pode “ocorrer” em outra. | Existem relações ''internas'' entre uma proposição e outra; mas uma proposição não pode ter com outra ''a'' relação interna que um ''nome'' tem com a proposição da qual seja constituinte e que deveria significar ao dizer que “ocorre” nela. Nesse sentido, uma proposição não pode “ocorrer” em outra. | ||
| Line 167: | Line 167: | ||
A proposição (∃x) . ϕx . x = a : = : ϕa pode ser vista como uma tautologia, se alguém expressas as ''condições'' de verdade de (∃x) . ϕx . x = a, sucessivamente, e.g., dizendo: isso é verdade ''se'' isso e aquilo, e isso novamente é verdade ''se'' isso e aquilo, etc., pois (∃x) . ϕx . x = a; e então também para ϕa. Expressar a questão desse modo é uma notação desajeitada, da qual a ab-notação é uma tradução mais arrumada. | A proposição (∃x) . ϕx . x = a : = : ϕa pode ser vista como uma tautologia, se alguém expressas as ''condições'' de verdade de (∃x) . ϕx . x = a, sucessivamente, e.g., dizendo: isso é verdade ''se'' isso e aquilo, e isso novamente é verdade ''se'' isso e aquilo, etc., pois (∃x) . ϕx . x = a; e então também para ϕa. Expressar a questão desse modo é uma notação desajeitada, da qual a ab-notação é uma tradução mais arrumada. | ||
O que simboliza em um símbolo é o que é comum a todos os símbolos que poderiam, de acordo com as regras da lógica = regras sintéticas para manipulação de símbolos, ser substituídos por ela. [Cf. 3.344.] | O que simboliza em um símbolo é o que é comum a todos os símbolos que poderiam, de acordo com as regras da lógica = regras sintéticas para manipulação de símbolos, ser substituídos por ela. <!-- [Cf. 3.344.] --> | ||
A questão sobre se uma proposição tem sentido (Sinn) nunca pode depender da ''verdade'' de outra proposição sobre um constituinte da primeira. E.g., a questão de se (x) x=x tem significado (Sinn)<ref>Possivelmente “entre as barras verticais (''Sheffer-strokes'')” [Edd.].</ref> não pode depender da questão se (∃x) x=x é ''verdadeiro''. Não descreve a realidade de nenhum modo, e lida unicamente com símbolos; e diz que eles devem ''simbolizar'', mas não ''o que'' eles simbolizam. | A questão sobre se uma proposição tem sentido (Sinn) nunca pode depender da ''verdade'' de outra proposição sobre um constituinte da primeira. E.g., a questão de se (x) x=x tem significado (Sinn)<!--<ref>Possivelmente “entre as barras verticais (''Sheffer-strokes'')” [Edd.].</ref>--> não pode depender da questão se (∃x) x=x é ''verdadeiro''. Não descreve a realidade de nenhum modo, e lida unicamente com símbolos; e diz que eles devem ''simbolizar'', mas não ''o que'' eles simbolizam. | ||
É óbvio que os pontos e colchetes são símbolos, e óbvio que eles não têm nenhum significado ''independente''. Você deve, portanto, para introduzir as chamadas “constantes lógicas” adequadamente, introduzir a noção geral de ''todas as possíveis'' combinações delas = a forma geral de uma proposição. Você, portanto, introduz ambas ab-funções, identidade e universalidade (as três constantes fundamentais) simultaneamente. | É óbvio que os pontos e colchetes são símbolos, e óbvio que eles não têm nenhum significado ''independente''. Você deve, portanto, para introduzir as chamadas “constantes lógicas” adequadamente, introduzir a noção geral de ''todas as possíveis'' combinações delas = a forma geral de uma proposição. Você, portanto, introduz ambas ab-funções, identidade e universalidade (as três constantes fundamentais) simultaneamente. | ||
| Line 179: | Line 179: | ||
A questão surge: como pode uma proposição (ou função) ocorrer em outra proposição? A proposição ou função por si só não pode possivelmente ficar em relação a outros símbolos. Por essa razão nós devemos introduzir funções assim como nomes de uma vez na nossa forma geral de uma proposição; explicando o que se quer dizer, atribuindo significado ao fato de que os nomes ficam entre a |,<ref>No original, “''meaning''” está traduzido por “significado” neste trabalho, e não “''sense''” como o substantivo em alemão “''Sinn''” entre parênteses pode sugerir.</ref> e que a função fica à esquerda dos nomes. | A questão surge: como pode uma proposição (ou função) ocorrer em outra proposição? A proposição ou função por si só não pode possivelmente ficar em relação a outros símbolos. Por essa razão nós devemos introduzir funções assim como nomes de uma vez na nossa forma geral de uma proposição; explicando o que se quer dizer, atribuindo significado ao fato de que os nomes ficam entre a |,<ref>No original, “''meaning''” está traduzido por “significado” neste trabalho, e não “''sense''” como o substantivo em alemão “''Sinn''” entre parênteses pode sugerir.</ref> e que a função fica à esquerda dos nomes. | ||
É verdadeiro, em certo sentido, que proposições lógicas são “postulados” – algo que nós “demandamos”; pois nós demandamos uma notação satisfatória. [Cf. 6.1223.] | É verdadeiro, em certo sentido, que proposições lógicas são “postulados” – algo que nós “demandamos”; pois nós demandamos uma notação satisfatória. <!-- [Cf. 6.1223.] --> | ||
Uma tautologia (''não'' uma proposição lógica), não é sem sentido da mesma forma em que, e.g., uma proposição na qual palavras que não têm significado ocorrem. O que acontece nela é que todas as suas partes simples têm significado, mas as conexões entre essas paralisam ou destroem umas às outras, de modo que elas todas estão conectadas somente numa maneira irrelevante. | Uma tautologia (''não'' uma proposição lógica), não é sem sentido da mesma forma em que, e.g., uma proposição na qual palavras que não têm significado ocorrem. O que acontece nela é que todas as suas partes simples têm significado, mas as conexões entre essas paralisam ou destroem umas às outras, de modo que elas todas estão conectadas somente numa maneira irrelevante. | ||
| Line 195: | Line 195: | ||
Diferentes tipos lógicos podem não ter nada em comum. Mas o mero fato de que nós podemos falar sobre a possibilidade de uma relação de n lugares, ou de uma analogia entre um com dois lugares e um com quatro, mostra que relações com diferentes números de lugares têm algo em comum, que, portanto, a diferença não é uma de tipo, mas como a diferença entre nomes diferentes – algo que depende da experiência. Isso responde a questão como podemos saber que realmente obtivemos a forma mais geral de uma proposição. Nós temos apenas introduzir o que é ''comum'' a todas as relações de qualquer número de lugares. | Diferentes tipos lógicos podem não ter nada em comum. Mas o mero fato de que nós podemos falar sobre a possibilidade de uma relação de n lugares, ou de uma analogia entre um com dois lugares e um com quatro, mostra que relações com diferentes números de lugares têm algo em comum, que, portanto, a diferença não é uma de tipo, mas como a diferença entre nomes diferentes – algo que depende da experiência. Isso responde a questão como podemos saber que realmente obtivemos a forma mais geral de uma proposição. Nós temos apenas introduzir o que é ''comum'' a todas as relações de qualquer número de lugares. | ||
A relação de “eu acredito p” para “p” pode ser comparada com a relação de ‘“p” diz (''besagt'') p’ para p: é tão impossível que ''eu'' deveria ser simples como “p” deveria ser. [Cf. 5.542.] | A relação de “eu acredito p” para “p” pode ser comparada com a relação de ‘“p” diz (''besagt'') p’ para p: é tão impossível que ''eu'' deveria ser simples como “p” deveria ser. <!-- [Cf. 5.542.] --> | ||
{{references}} | {{references}} | ||
[[Category:Previously unpublished translations]] | [[Category:Previously unpublished translations]] | ||
Revision as of 17:31, 23 August 2024
Ludwig Wittgenstein
Notas Ditadas a G.E. Moore na Noruega
Tradução de Melina Bentes
Esta tradução está baseada na edição Ludwig Wittgenstein, Notes Dictated to G. E. Moore in Norway, Appendix II from Notebooks 1914-1916, edited by G. H. Von Wright and G. E. M. Anscombe, Harper Torchbooks, New York: Harper & Row Publishers, 2nd edition, 1984, e foi revisada por Cristiano Moita. O texto da língua original está em domínio público no seu país de origem e em outros países e áreas onde o período de proteção dos direitos autorais é igual à vida do autor mais 70 anos ou menos. Esta tradução está publicada no website do Projeto Ludwig Wittgenstein sob os termos da licença Creative Commons Atribuição-CompartilhaIgual.
Ludwig Wittgenstein
Notas Ditadas a G.E. Moore na Noruega
Abril, 1914
Proposições assim chamadas lógicas mostram [as] propriedades lógicas da linguagem, e portanto, do Universo, mas nada dizem.
Isso significa que, por meramente olhar para elas, você consegue ver essas propriedades; enquanto que, em uma proposição adequada, você não consegue ver o que é verdade, apenas olhando para ela.
É impossível dizer o que essas propriedades são, pois, para fazer isso,você precisaria de uma linguagem, que não possui as propriedades em questão, e é impossível que isso seja uma linguagem própria. Impossível construir [uma] linguagem ilógica.
Para que você tenha uma linguagem que consegue expressar ou dizer tudo o que pode ser dito, essa linguagem precisa ter certas propriedades; e quando este é o caso, quando as tem, não pode mais ser dito naquela linguagem ou em qualquer linguagem
Uma linguagem ilógica seria uma em que, e.g. [exempli gratia = por exemplo], você poderia colocar um evento em um buraco.
Assim a linguagem que possa expressar qualquer coisa espelha certas propriedades do mundo, por essas propriedades que ela precisa ter; e proposições assim chamadas lógicas mostram de um modo sistemático essas propriedades.
Como, geralmente, proposições lógicas mostram essas propriedades funciona assim: Nós damos uma certa descrição para uma espécie de símbolo; nós descobrimos que outros símbolos, combinados de certos modos, produzem um símbolo dessa descrição; e que elas mostram algo sobre esses símbolos.
Em regra, a descrição [fornecida] na Lógica ordinária é a descrição de uma tautologia; mas outras podem expor igualmente bem, e.g., uma contradição.
Toda proposição real mostra alguma coisa, além do que diz, sobre o Universo: pois, se ela não tem sentido, não pode ser utilizada; e se tem sentido, ela espelha alguma propriedade lógica do Universo.
E.g., considere ϕa, ϕa ⊃ ψa, ψa. Por meramente olhar esses três [símbolos], eu posso perceber que 3 se segue de 1 e 2; i.e. eu posso perceber o que é chamado de verdade de uma proposição lógica, isto é, d[a] proposição ϕa. ϕa ⊃ ψa : ⊃ : ψa. Mas isso não é uma proposição; pois, ao perceber que isso é uma tautologia, eu posso ver o que eu já vi ao olhar as três proposições: a diferença é que agora eu vejo que aquilo é uma tautologia. .
Nós queremos dizer que, para entender [o] dito acima, quais propriedades um símbolo deve ter, para que seja uma tautologia.
Muitos modos possíveis de dizer isto são possíveis:
Uma é fornecer certos símbolos; em seguida, fornecer um conjunto de regras para combiná-los; então dizer: qualquer símbolo formado por esses símbolos, combinando-os de acordo com uma das regras fornecidas, é uma tautologia. Isso obviamente diz algo sobre o tipo de símbolo que você pode ter nesse modo.
Esse é o procedimento d[a] chamada Lógica antiga: fornece proposições primitivas; chamadas regras de dedução; e então diz o que você tem aplicando as regras às proposições, é uma proposição lógica que você provou. A verdade é, ela diz algo sobre o tipo de proposição que você tem, viz. [videlicet = isto é] que ela pode ser derivada dos primeiros símbolos por essas regras de combinação (= é uma tautologia).
Assim, se dissermos que uma proposição lógica se segue logicamente de outra, isso quer dizer algo bem diferente de dizer que uma proposição real se segue logicamente de outra. Pois a chamada prova de uma proposição lógica não prova sua verdade (proposições lógicas não são nem verdadeiras nem falsas) mas prova que é uma proposição lógica (= é uma tautologia).
Proposições lógicas são formas de prova: elas mostram que uma ou mais proposições se seguem de uma (ou mais).
Proposições lógicas mostram algo, porque a linguagem na qual elas são expressadas pode dizer tudo o que pode ser dito.
Essa mesma distinção entre o que pode ser exposto pela linguagem, mas não pode ser dito, explica a dificuldade que se sente sobre os tipos – e.g, assim como [a] diferença entre coisas, fatos, propriedades, relações. Que M é uma coisa não pode ser dito; não tem sentido: mas algo é exposto pelo símbolo “M”. Do mesmo modo, que uma proposição é uma proposição de sujeito-predicado, não pode ser dito: mas isso é exposto pelo símbolo.
Portanto, uma Teoria dos Tipos é impossível. Ela tenta dizer algo sobre os tipos, quando você só pode falar sobre os símbolos. Mas o que você diz sobre os símbolos não é que esse símbolo tem aquele tipo, que seria sem sentido pela mesma razão: mas você diz simplesmente: Esse é o símbolo, para prevenir um mal-entendido. E.g., em “aRb”, “R” não é um símbolo, mas que “R” simboliza que ele está entre um nome e outro. Aqui nós não dissemos: esse símbolo não é desse tipo mas daquele, mas apenas: isto simboliza e não aquilo. Isso parece, novamente, cometer o mesmo erro, porque “simboliza” é “tipicamente ambíguo”. A verdadeira análise é: “R” não é um nome próprio e que [quando] “R” fica entre “a” e “b” expressa uma relação. Aqui estão duas proposições de tipos diferentes conectadas por “e”.
É óbvio que, e.g., com uma proposição de sujeito-predicado, se ela tem algum sentido, você vê a forma, tão logo você entende a proposição, apesar de não saber se ela é verdadeira ou falsa. Mesmo que houvesse proposições da forma “M é uma coisa” elas seriam supérfluas (tautológicas) pois o que ela tenta dizer é algo que já é visto quando você vê “M”.
Na expressão acima “aRb”, nós estamos falando apenas deste “R” em particular, enquanto que o que queremos fazer é falar de todos os símbolos similares. Devemos dizer: em qualquer símbolo dessa forma, o que corresponde a “R” não é um nome próprio, e o fato que [“R” está entre “a” e “b”] expressa uma relação. É isso que se procurou ser expresso pela afirmação sem sentido: símbolos como esse são de um certo tipo. Isso você não pode dizer, pois para dizê-lo é preciso primeiro saber o que o símbolo é: e ao saber isso você vê [o] tipo e assim também [o] tipo [do que está] simbolizado. I.e. [id est = ou seja] ao saber o que [o símbolo] simboliza, você sabe tudo o que há para saber; você não pode dizer nada sobre o símbolo.
Por exemplo: considere as duas proposições (1) “O que [se] simboliza aqui é uma coisa”, (2) “O que [se] simboliza aqui é um fato relacional (= relação)”. Essas {proposições} são sem sentido por duas razões: (a) porque elas mencionam “coisa” e “relação”; (b) porque elas as mencionam (coisa e relação) em proposições da mesma forma. As duas proposições precisam ser expressadas em formas inteiramente diferentes, se propriamente analisadas; e nem a palavra “coisa” ou “relação” devem ocorrer.
Agora, veremos como analisar corretamente as proposições em que “coisa”, “relação”, etc., ocorrem.
(1) Considere ϕx. Nós queremos explicar o significado de ‘Em “ϕx” uma coisa [se] simboliza’. A análise é: –
(∃y) . y simboliza . y = “x” . “ϕx”
[“x” é o nome de y: “ϕx” = ‘“ϕ” está na esquerda de “x”’ e diz ϕx.]
N.B. “x” não pode ser o nome desse rascunho original y, porque isso não é uma coisa: mas pode ser o nome de uma coisa; e nós precisamos entender que o que estamos fazendo é explicar o que significaria dizer de um símbolo ideal, que consistia efetivamente no fato de uma coisa estar à esquerda de outra, que nele uma coisa simbolizava.
(N.B. N[a] expressão (∃y).ϕy, alguém está apto a dizer [que] isso significa “Existe uma coisa tal que…”. Mas, na verdade, nós deveríamos dizer “Existe um y, tal que…”; o fato de que y simboliza expressar o que queremos dizer.)
Em geral: Quando tais proposições são analisadas, enquanto as palavras “coisa”, “fato”, etc. vão desaparecer, vão aparecer, em vez delas, um novo símbolo, da mesma forma que aquele do qual estamos falando; e, por isso, será imediatamente óbvio que nós não podemos obter um tipo de proposição a partir de outra por substituição.
Na nossa linguagem, nomes não são coisas: nós não sabemos o que eles são: tudo o que nós sabemos é que eles são de um tipo diferente das relações, etc. etc. O tipo de um símbolo de uma relação é parcialmente fixado [pelo] tipo de [um] símbolo de [uma] coisa, já que o símbolo [do] último tipo deve ocorrer.
N.B. Em qualquer proposição ordinária, e.g., “Moore bom”, isso mostra e não diz que “Moore” está à esquerda de “bom”; e aqui o que é exposto pode ser dito por outra proposição. Mas isso só se aplica para aquela parte do que está sendo exposto que é arbitrária. As propriedades lógicas que ela mostra não são arbitrárias, e que ela as tem não pode ser dito em nenhuma proposição.
Quando nós falamos uma proposição d[a] forma “aRb” que o que ela simboliza é que “R” está entre “a” e “b”, é preciso ser lembrado que na verdade a proposição é capaz de uma análise mais aprofundada pois a, R, e b não são simples. Mas o que parece certo é que quando a tivermos analisado, nós devemos, ao final, chegar em proposições da mesma forma a respeito do fato que elas consistem em uma coisa estando entre duas outras.
Como podemos falar da forma geral de uma proposição, sem conhecer nenhuma proposição não analisável, em que ocorrem nomes e relações particulares? O que nos justifica em fazer isso é que, ainda que nós não conheçamos nenhuma proposição não analisável desse tipo, ainda assim nós conseguimos entender o que se quer dizer com uma proposição dessa forma (∃x, y, R), xRy (que não é analisável), mesmo que nós conheçamos nenhuma proposição da forma xRy.
Se você tivesse qualquer proposição não analisável na qual ocorressem nomes e relações particulares (e proposição não analisável = uma na qual apenas símbolos fundamentais = aqueles que não são sujeitos a definição, ocorrem) então você pode sempre formar dela uma proposição da forma (∃x, y, R). xRy, que embora não contenha nenhum nome e relação particulares, é não analisável.
(2) O ponto pode ser abordado como se segue. Pegue ϕa e ϕA: e pergunte o que se quer dizer com “Tem uma coisa em ϕa, e uma complexa em ϕA”?
(1) quer dizer: (∃x) . ϕx . x = a
(2) quer dizer: (∃x, ψξ) . ϕA = ψx . ϕx.
Uso de proposições lógicas. Você pode ter uma tão complicada que você não consegue, ao olhar para ela, ver que é uma tautologia; mas você mostrou que pode ser derivada por determinas operações a partir de certas outras proposições de acordo com nossa regra para construir tautologias; e assim você está habilitado para ver que uma coisa se segue da outra, quando você não seria capaz de ver isso de outro modo. E.g., se nossa tautologia é d[a] forma p ⊃ q você pode ver que p se segue de p; e assim por diante.
O significado [Bedeutung] de uma proposição é o fato que corresponde a ela, e.g., se nossa proposição “aRb”, se for verdadeira, o fato correspondente seria o fato aRb, se for falsa, o fato ~aRb. Mas ambos “o fato aRb” e “o fato ~aRb” são símbolos incompletos, os quais precisam ser analisados.
Que a proposição tem uma relação (no sentido amplo) com a Realidade, outra que o significado [Bedeutung], é mostrado pelo fato de que você pode entendê-la quando você não sabe o significado [Bedeutung], i.e. não sabe se é verdadeiro ou falso. Vamos expressar isso ao dizer “Ela [proposição] tem um sentido” (Sinn).
Analisando o significado [Bedeutung], você chega ao sentido [Sinn] seguinte:
Nós queremos explicar a relação das proposições com a realidade.
A relação é a seguinte: Seus simples têm significado = são nomes de simples; e suas relações tem uma relação bem diferente com relações; e esses dois fatos já estabelecem uma espécie de correspondência entre a proposição que contém esses, e apenas esses, e a realidade: i.e. se todos os simples de uma proposição são conhecidos, nós já sabemos que podemos descrever a realidade ao dizer que ela se comporta de um certo modo para o todo da proposição. (Isso equivale dizer que nós podemos comparar realidade com proposição. No caso de duas linhas, nós podemos compará-las em relação ao seu comprimento sem nenhuma convenção: a comparação é automática. Mas no nosso caso a possibilidade da comparação depende das convenções pelas quais nós damos sentido aos nossos simples (nomes e relações).
Apenas resta fixar o método de comparação ao dizer o quê sobre nossos simples é dizer o quê sobre a realidade. E.g., suponha que peguemos duas linhas de comprimentos diferentes: e dizemos que o fato de a menor ser de um comprimento que é quer dizer que a maior é do comprimento que ela é. Nós deveríamos então ter estabelecido uma convenção quanto ao sentido da menor, do tipo que vamos dar agora.
Disso resulta que “verdadeiro” e “falso” não são propriedades acidentais de uma proposição, tanto que, quando ela tem significado, nós podemos dizer que é também verdadeira ou falsa: do contrário, ter significado significa ser verdadeira ou falsa: o ser verdadeira ou falsa na verdade constitui a relação da proposição com a realidade, a qual exprimimos ao dizer que tem sentido (Sinn).
Parece existir à primeira vista uma certa ambiguidade no que significa dizer que uma proposição é “verdadeira”, devido ao fato que parece como se, no caso de diferentes proposições, o modo como elas correspondem aos fatos aos quais correspondem é bem diferente. Mas o que é realmente comum em todos os casos é que eles devem ter a forma geral de uma proposição. Ao fornecer a forma geral de uma proposição, você está explicando quais tipos de modos de juntar os símbolos de coisas e relações vai corresponder às (se análoga às) coisas) que têm essas relações na realidade. Ao fazer desse modo você está dizendo o que significa dizer que uma proposição é verdadeira; e você deve fazer isso de uma vez por todas. Ao dizer “Essa proposição tem sentido” significa ‘“Essa proposição é verdadeira” significa…’ (“p” é verdadeiro = “p”. p . Def. : apenas em vez de “p” nós devemos introduzir a forma geral de uma proposição).
Parece à primeira vista como se a notação ab devesse ser falsa, pois parece tratar verdadeiro e falso como se estivessem exatamente no mesmo nível. Deve ser possível ver a partir dos símbolos mesmos que existe uma diferença essencial entre os polos, se a notação for correta; e parece como se de fato isso fosse impossível.
A interpretação de um simbolismo não deve depender de dar uma interpretação diferente a símbolos do mesmo tipo.
Como assimetria é introduzida pelo fornecimento de uma descrição de forma particular de símbolo que nós chamamos de “tautologia”. A descrição do ab-símbolo sozinha é simétrica em relação a a e b; mas essa descrição, mais o fato de que o que satisfaz a descrição de uma tautologia é uma tautologia é assimétrica em relação a eles. Dizer que uma descrição era simétrica em relação a dois símbolos significaria que nós poderíamos substituir um pelo outro, e ainda assim a descrição permanece a mesma, i.e. significa o mesmo).
Pegue p.q e q. Quando você escreve p.q na notação ab, é impossível ver do símbolo sozinho que q se segue dele, pois, se você fosse interpretar o polo verdadeiro como falso, o mesmo símbolo iria significar p ∨ q, do qual q não se segue. Mas no momento em que você diz quais símbolos são tautologias, imediatamente se torna possível ver do fato de que eles são e o símbolo original que se segue de q.
Proposições lógicas, é claro, todas mostram algo diferente: todas elas mostram, do mesmo modo, viz. pelo fato de que elas são tautologias, mas elas são diferentes tautologias e portanto cada uma mostra algo diferente.
O que é não-arbitrário sobre nossos símbolos não são eles, nem as regras que damos; mas o fato de que, tendo dadas certas regras, outras são fixadas = se seguem logicamente.
Assim, embora fosse possível interpretar a forma que tomamos como a forma de uma tautologia, como de uma contradição e vice versa, elas são diferentes na forma lógica porque, apesar da forma aparente dos símbolos ser a mesma, o que simboliza neles é diferente, e por isso o que se segue sobre os símbolos de uma interpretação vai ser diferente do que se segue de outra. Mas a diferença entre a e b não é uma forma lógica, de modo que nada vai se seguir dessa diferença sozinha quanto a interpretação de outros símbolos. Então, e.g., p.q., p ∨ q parecem símbolos da exata mesma forma lógica na notação ab. Ainda assim elas dizem algo inteiramente diferente; e, se você perguntar por quê, a resposta parece ser: Em um caso o esboço em cima tem o formato b, em outro o formato a. Enquanto que a interpretação de uma tautologia como uma tautologia é uma interpretação de uma forma lógica, não o fornecimento de um significado para o rascunho de uma forma particular. O que importa é que a interpretação da forma do simbolismo deve ser fixada dando uma interpretação para suas propriedades lógicas, e não dando interpretações para rascunhos particulares.
Constantes lógicas não podem ser transformadas em variáveis: porque nelas o que simboliza não é o mesmo; todos os símbolos pelos quais uma variável pode ser substituída simbolizam no mesmo sentido.
Nós descrevemos um símbolo, e dizemos arbitrariamente “Um símbolo dessa descrição é uma tautologia”. E assim, segue-se de uma vez, tanto que qualquer outro símbolo que responda à mesma descrição seja uma tautologia e que qualquer símbolo que não o faça não seja. Isto é, nós arbitrariamente fixamos que qualquer símbolo daquela descrição é para ser uma tautologia; e isso sendo fixado, não é mais arbitrário no que diz respeito a qualquer outro símbolo, quer seja uma tautologia ou não.
Havendo assim fixado o que é uma tautologia e o que não é, nós podemos então, havendo fixado arbitrariamente de novo que a relação a-b é transitiva, obtida dos dois fatos juntos de que “p ≡ ~(~p)” é uma tautologia. Porque ~(~p) = a-b-a-p-b-a-b. O ponto é: que o processo de raciocínio pelo qual chegamos ao resultado que a-b-a-p-b-a-b é o mesmo símbolo que a-p-b, é exatamente o mesmo que aquele pelo qual nós descobrimos que seu significado é o mesmo, viz. onde raciocinamos se b-a-p-b-a, então não a-p-b, se a-b-a-p-b-a-b então não b-a-p-b-a, portanto se a-b-a-p-b-a-b, então a-p-b.
Segue-se o fato de que a-b é transitivo que, onde temos a-b-a, o primeiro a tem com o segundo a mesma relação que tem com b. É o mesmo com o fato de que a-verdadeiro implica b-falso, e b-falso implica c-verdadeiro, nós entendemos que a-verdadeiro implica c-verdadeiro. E nós devemos ser capazes de ver que, havendo fixado a descrição de uma tautologia, que p ≡ ~(~p) é uma tautologia.
Que, quando certa regra é dada, um símbolo mostra uma verdade lógica.
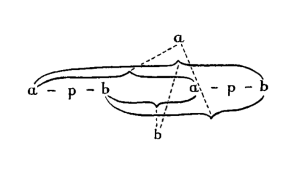
Esse símbolo pode ser interpretado como uma tautologia ou uma contradição.
Ao estabelecer que deve ser interpretado como uma tautologia e não como uma contradição, eu não estou atribuindo um significado para a e b; i.e. dizendo que eles simbolizam coisas diferentes, mas do mesmo modo. O que eu estou fazendo é dizer que o modo como o polo-a está conectado com o símbolo todo simboliza de um modo diferente do que simbolizaria se o símbolo fosse interpretado como uma contradição. E eu adiciono os riscos a e b meramente para mostrar quais sentidos a conexão está simbolizando, de modo que possa ser evidente que, onde quer que o mesmo risco ocorra no lugar correspondente a outro símbolo, também aí a conexão estará simbolizando do mesmo modo.
Nós poderíamos, é claro, simbolizar qualquer ab-função sem utilizar dois polos externos, meramente, e.g., omitindo o polo b; e aqui o que iria simbolizar seria que os três pares internos dos polos das proposições seriam conectados de certo modo com o polo a, enquanto o outro par não estaria conectado a ele. E então a diferença entre os riscos a e b, onde nós os usamos, meramente mostram que é um diferente estado de coisas que está simbolizando um caso e outro: em um caso, que certos polos internos estão conectados em um certo modo com um polo externo, no outro caso, que eles não estão conectados.
O símbolo para uma tautologia, de qualquer forma que colocamos, e.g., quer omitindo o polo a ou omitindo o b, seria sempre capaz de ser usado como o símbolo para uma contradição; apenas não na mesma linguagem.
A razão pela qual ~x é sem significado é simplesmente que nós demos nenhum sentido para o símbolo ~ξ. I.e. enquanto ϕx e ϕp parecem ser do mesmo tipo, eles não são porque, para dar um significado para ~x, você deveria ter alguma propriedade ~ξ. O que simboliza em ϕξ é que ϕ está à esquerda de um nome próprio e obviamente isso não é assim em ~p. O que é comum a todas proposições em que o nome de uma propriedade (para falar frouxamente) ocorre é que esse nome está à esquerda de uma forma-nome.
A razão pela qual, e.g., parece que “Platão Sócrates” pode ter significado, enquanto “Abracadabra Sócrates” nunca vai ser suspeito de ter um, é porque nós sabemos que “Platão” tem um e não observamos que, para que a frase inteira devesse ter um, o que é necessário não é que “Platão” devesse ter um, mas que o fato de que “Platão estar à esquerda de um nome deve”.
A razão pela qual “A propriedade de não ser verde não é verde” é sem sentido, porque nós apenas damos significado ao fato de que “verde” está à direita de um nome; e “a propriedade de não ser verde” obviamente não é isso.
ϕ não pode possivelmente estar à esquerda de (ou em qualquer outra relação com) o símbolo de uma propriedade. Então o símbolo de uma propriedade, e.g., ψx é que ψ está à esquerda de uma forma-nome, e outro símbolo ϕ não pode possivelmente estar à esquerda de tal fato: se pudesse, nós deveríamos ter uma linguagem ilógica, o que é impossível.
p é falso = ~(p é verdadeiro) Def.
É muito importante que as aparentes relações lógicas ∨, ⊃, etc. precisem de colchetes, pontos, etc., i.e. ter “gamas”; que por si só mostra que eles não são relações. Esse fato tem sido menosprezado, porque é muito universal – a coisa mesma que deixa isso importante.
Existem relações internas entre uma proposição e outra; mas uma proposição não pode ter com outra a relação interna que um nome tem com a proposição da qual seja constituinte e que deveria significar ao dizer que “ocorre” nela. Nesse sentido, uma proposição não pode “ocorrer” em outra.
Relações internas são relações entre tipos, que não podem ser expressadas em proposições, mas estão todas à mostra nos símbolos em si mesmos e podem ser exibidas sistematicamente em tautologias. Por que nós a chamamos de “relações” é porque proposições lógicas têm uma relação análoga a elas, para a qual proposições propriamente relacionais têm com relações.
Proposições podem ter muitas relações internas diferentes umas com as outras. A única que nos autoriza deduzir uma da outra é se, digamos, elas são ϕa e ϕa ⊃ ψa, então ϕa . ϕa ⊃ ψa : ⊃ : ψa é uma tautologia.
O símbolo de identidade expressa uma relação interna entre a função e o seu argumento: i.e. ϕa = (∃x) . ϕx . x = a.
A proposição (∃x) . ϕx . x = a : = : ϕa pode ser vista como uma tautologia, se alguém expressas as condições de verdade de (∃x) . ϕx . x = a, sucessivamente, e.g., dizendo: isso é verdade se isso e aquilo, e isso novamente é verdade se isso e aquilo, etc., pois (∃x) . ϕx . x = a; e então também para ϕa. Expressar a questão desse modo é uma notação desajeitada, da qual a ab-notação é uma tradução mais arrumada.
O que simboliza em um símbolo é o que é comum a todos os símbolos que poderiam, de acordo com as regras da lógica = regras sintéticas para manipulação de símbolos, ser substituídos por ela.
A questão sobre se uma proposição tem sentido (Sinn) nunca pode depender da verdade de outra proposição sobre um constituinte da primeira. E.g., a questão de se (x) x=x tem significado (Sinn) não pode depender da questão se (∃x) x=x é verdadeiro. Não descreve a realidade de nenhum modo, e lida unicamente com símbolos; e diz que eles devem simbolizar, mas não o que eles simbolizam.
É óbvio que os pontos e colchetes são símbolos, e óbvio que eles não têm nenhum significado independente. Você deve, portanto, para introduzir as chamadas “constantes lógicas” adequadamente, introduzir a noção geral de todas as possíveis combinações delas = a forma geral de uma proposição. Você, portanto, introduz ambas ab-funções, identidade e universalidade (as três constantes fundamentais) simultaneamente.
A proposição variável p ⊃ p não é idêntica à proposição variável ~(p.~p). As universais correspondentes seriam idênticas. A proposição variável ~(p.~p) mostra que de ~(p.q) você obtém uma tautologia substituindo ~p por q, enquanto a outra não mostra isso.
É muito importante perceber que, quando você tem duas relações diferentes (a,b)R, (c,d)S, isso não estabelece uma correlação entre a e c, e b e d, ou a e d, e b e c: não existe nenhuma correlação assim estabelecida. É claro, no caso de dois pares de termos unidos pela mesma relação, existe uma correlação. Isso mostra que a teoria que sustentou que um fato relacional contendo os termos e as relações unidos por uma cópula (ε2) é uma inverdade; pois, se isso fosse o caso, existiria uma correspondência entre os termos de diferentes relações.
A questão surge: como pode uma proposição (ou função) ocorrer em outra proposição? A proposição ou função por si só não pode possivelmente ficar em relação a outros símbolos. Por essa razão nós devemos introduzir funções assim como nomes de uma vez na nossa forma geral de uma proposição; explicando o que se quer dizer, atribuindo significado ao fato de que os nomes ficam entre a |,[1] e que a função fica à esquerda dos nomes.
É verdadeiro, em certo sentido, que proposições lógicas são “postulados” – algo que nós “demandamos”; pois nós demandamos uma notação satisfatória.
Uma tautologia (não uma proposição lógica), não é sem sentido da mesma forma em que, e.g., uma proposição na qual palavras que não têm significado ocorrem. O que acontece nela é que todas as suas partes simples têm significado, mas as conexões entre essas paralisam ou destroem umas às outras, de modo que elas todas estão conectadas somente numa maneira irrelevante.
Funções lógicas todas pressupõem umas às outras. Assim como podemos ver que ~p não tem sentido, se p não tem nenhum; então também podemos dizer p não tem se ~p não tem. O caso é bem diferente com ϕa e a: pois aqui a tem significado independentemente de ϕa, ainda que ϕa pressuponha isso.
As constantes lógicas parecem ser símbolos-complexos, mas, por outro lado, elas podem ser intercambiadas umas pelas outras. Elas não são, portanto, realmente complexas; o que simboliza é simplesmente a forma geral em que elas são combinadas.
A combinação de símbolos em uma tautologia não pode corresponder possivelmente a nenhuma combinação particular de seus significados – ela corresponde a toda combinação possível; e, portanto, o que simboliza não pode ser a conexão dos símbolos.
Do fato de que eu vejo que um ponto está à esquerda de outro, ou de que uma cor é mais escura que outra, parece se seguir de que isso é o caso; e, se for o caso, só pode ser se existir uma relação interna entre os dois; e nós podemos expressar isso ao dizer que a forma do último é parte da forma do primeiro. Nós podemos então dar um sentido para a assertiva que leis lógicas são formas de pensamento, espaço e tempo, formas de intuição.
Diferentes tipos lógicos podem não ter nada em comum. Mas o mero fato de que nós podemos falar sobre a possibilidade de uma relação de n lugares, ou de uma analogia entre um com dois lugares e um com quatro, mostra que relações com diferentes números de lugares têm algo em comum, que, portanto, a diferença não é uma de tipo, mas como a diferença entre nomes diferentes – algo que depende da experiência. Isso responde a questão como podemos saber que realmente obtivemos a forma mais geral de uma proposição. Nós temos apenas introduzir o que é comum a todas as relações de qualquer número de lugares.
A relação de “eu acredito p” para “p” pode ser comparada com a relação de ‘“p” diz (besagt) p’ para p: é tão impossível que eu deveria ser simples como “p” deveria ser.
- ↑ No original, “meaning” está traduzido por “significado” neste trabalho, e não “sense” como o substantivo em alemão “Sinn” entre parênteses pode sugerir.
