Algunas observaciones sobre la forma lógica: Difference between revisions
No edit summary |
No edit summary |
||
| Line 13: | Line 13: | ||
Si tratamos de analizar cualquier proposición nos daremos cuenta, en general, que son sumas lógicas, productos u otras funciones de verdad de proposiciones más simples. Pero nuestro análisis, si es llevado lo suficientemente lejos, debe llegar al punto donde alcanza formas proposicionales que no están compuestas por | Toda proposición tiene un contenido y una forma. Nosotros adquirimos la imagen de la forma pura si abstraemos del significado de las palabras individuales, o símbolos (en la medida que tienen significados independientes). Esto es, si sustituimos variables por las constantes de la proposición. Las reglas de la sintaxis que son aplicadas a las constantes deben aplicarse también a las variables. Por sintaxis, en este sentido general de la palabra, me refiero a las reglas que nos dicen solo en qué conexiones una palabra tiene sentido, excluyendo así estructuras sin sentido. La sintaxis del lenguaje ordinario, como es bien conocido, no es muy adecuada a este propósito. No impide en todos los casos la construcción de pseudoproposiciones sin sentido (construcciones como “el rojo es más alto que el verde” o “lo Real, aunque es un ''en sí mismo'', también debe ser capaz de convertirse en un ''para mí mismo”'', etc.). | ||
Si tratamos de analizar cualquier proposición dada nos daremos cuenta, en general, que son sumas lógicas, productos u otras funciones de verdad de proposiciones más simples. Pero nuestro análisis, si es llevado lo suficientemente lejos, debe llegar al punto donde alcanza formas proposicionales que no están a su vez compuestas por formas proposicionales más simples. Debemos finalmente llegar a la conexión definitiva de los términos, la conexión inmediata que no puede ser rota sin destruir la forma proposicional como tal. Las proposiciones que representan esta conexión definitiva de los términos las llamo, por B. Russell, proposiciones atómicas. Ellas, entonces, son el núcleo de todas las demás proposiciones, ''ellas'' contienen el material, y todo el resto es solo un desarrollo de este material. Son ellas las que tenemos que observar para hallar el objeto de las proposiciones. Es la tarea de la teoría del conocimiento encontrarlas y entender su construcción a partir de palabras o símbolos. Esta tarea es muy difícil, y la Filosofía apenas ha empezado a abordarla en ciertos puntos. ¿Qué método tenemos para abordarla? La idea es expresar en un simbolismo apropiado lo que en el lenguaje ordinario lleva a un sinfín de malentendidos. Esto es, donde el lenguaje ordinario oculta la estructura lógica, donde permite la formación de pseudoproposiciones, donde usa un término en una infinidad de significados diferentes, debemos reemplazarlo por un simbolismo que dé una imagen clara de la estructura lógica, excluya pseudoproposiciones y use sus términos sin ambigüedad. Ahora, solo podemos sustituir un simbolismo claro por el impreciso inspeccionando el fenómeno que queremos describir, tratando así de entender su multiplicidad lógica. Esto es, sólo podemos llegar al análisis correcto a través de, lo que puede ser llamado, la investigación lógica de los fenómenos mismos, esto es, en cierto sentido ''a posteriori'', y no haciendo conjeturas sobre posibilidades ''a priori.'' Uno suele sentirse tentado a preguntar desde una óptica ''a priori'': Qué, después de todo, ''pueden'' ser las únicas formas de proposiciones atómicas y contestar, por ejemplo, sujeto-predicado y relaciones proposicionales con dos o más términos, quizá, proposiciones que relacionan predicados y relaciones entre ellos, y así sucesivamente. Pero esto, creo, solamente es jugar con las palabras. Una forma atómica no puede ser prevista. Y sería sorprendente si el fenómeno real no tuviera nada más que enseñarnos sobre su estructura. A estas conjeturas sobre la estructura de las proposiciones atómicas somos llevados por nuestro lenguaje ordinario, que usa la estructura sujeto-predicado y la forma relacional. Pero esto en nuestro lenguaje es engañoso: Trataré de explicarlo con un símil. Imaginemos dos planos paralelos, I y II. En el plano I se dibujan figuras, por ejemplo, elipses y rectángulos de diferentes tamaños y formas, y nuestra es tarea producir imágenes de estas figuras en el plano II. Luego podemos imaginar dos maneras, entre otras, para hacer esto. Podemos, en primer lugar, establecer una ley de proyección—puede ser la de proyección ortogonal o cualquier otra—y luego proceder a proyectar todas las figuras de I a II, según esta ley. O, en segundo lugar, podemos proceder así: Establecemos la ley de que cada elipse en el plano I debe aparecer como un círculo en el plano II, y cada rectángulo como cuadrado en II. Tal forma de representación puede ser conveniente para nosotros si por alguna razón preferimos sólo dibujar círculos y cuadrados en el plano II. Por supuesto, de estas imágenes las formas exactas de las figuras originales del plano I no puedes ser inferidas inmediatamente. Solamente podemos saber a través de ellas que el original era una elipse o un rectángulo. Para conseguir la forma determinada del original en una sola instancia, tendríamos que saber el método individual por el cual, por ejemplo, una elipse particular es proyectada en el círculo ante mí. El caso del lenguaje ordinario es bastante análogo. Si los hechos de la realidad son los elipses y rectángulos del plano I, la estructura sujeto-predicado y las formas relacionales corresponden a los círculos y cuadrados del plano II. Estas formas son las reglas de nuestro lenguaje particular en el cual proyectamos ''en'' ''tantas maneras diferentes'' formas lógicas ''diferentes en tantas maneras.'' Y por esta razón no podemos sacar conclusiones—excepto unas muy vagas—del uso de estas reglas como la forma lógica real del fenómeno descrito. Formas como “Este artículo es aburrido”, “El clima está bien”, “Soy perezoso”, que no tienen nada que ver entre ellas, se presentan como proposiciones sujeto-predicado, esto es, aparentemente como proposiciones de la misma forma. | |||
Si, ahora, tratamos de llegar a un análisis real, encontramos formas lógicas que poca similitud tienen con las reglas del lenguaje ordinario. Nos encontramos con las formas del espacio y el tiempo con todo el conjunto de la variedad espacial y objetos temporales, como colores, sonidos, etc., etc., con sus graduaciones, transiciones continuas y combinaciones en proporciones varias, todas las cuales no pueden ser captadas por nuestros medios ordinarios de expresión. Y aquí deseo hacer mi primera observación definitiva en el análisis lógico de los fenómenos reales: es por esto, que para su representación números (racionales e irracionales) deben entrar en la estructura de las proposiciones atómicas mismas. Ilustraré esto con un ejemplo. Imagine un sistema de ejes rectangulares, por así decirlo, cables cruzados, dibujados en nuestro campo de visión y una escala arbitraria fijada. Entonces es claro que podemos describir la forma y posición de cada parche de color en nuestro campo visual por medio de declaraciones de números que tengan su significado relativo al sistema de coordenadas y la unidad escogida. De nuevo, es claro que esta descripción tendrá la multiplicidad lógica correcta, y que una descripción que tenga menos multiplicidad no servirá. Un simple ejemplo sería la representación de un parche P por la expresión “[6-9, 3-8]” y de una proposición sobre esta, | Si, ahora, tratamos de llegar a un análisis real, encontramos formas lógicas que poca similitud tienen con las reglas del lenguaje ordinario. Nos encontramos con las formas del espacio y el tiempo con todo el conjunto de la variedad espacial y objetos temporales, como colores, sonidos, etc., etc., con sus graduaciones, transiciones continuas y combinaciones en proporciones varias, todas las cuales no pueden ser captadas por nuestros medios ordinarios de expresión. Y aquí deseo hacer mi primera observación definitiva en el análisis lógico de los fenómenos reales: es por esto, que para su representación números (racionales e irracionales) deben entrar en la estructura de las proposiciones atómicas mismas. Ilustraré esto con un ejemplo. Imagine un sistema de ejes rectangulares, por así decirlo, cables cruzados, dibujados en nuestro campo de visión y una escala arbitraria fijada. Entonces es claro que podemos describir la forma y posición de cada parche de color en nuestro campo visual por medio de declaraciones de números que tengan su significado relativo al sistema de coordenadas y la unidad escogida. De nuevo, es claro que esta descripción tendrá la multiplicidad lógica correcta, y que una descripción que tenga menos multiplicidad no servirá. Un simple ejemplo sería la representación de un parche P por la expresión “[6-9, 3-8]” y de una proposición sobre esta, | ||
Revision as of 11:20, 15 January 2022
Ludwig Wittgenstein
Algunas observaciones sobre la forma lógica
Traducción: Luis Alejandro Castro McCausland
Esta traducción se basa en Ludwig Wittgenstein. «Some Remarks on Logical Form». Proceedings of the Aristotelian Society, Supplementary Volume 9 (Knowledge, Experience and Realism), 1929, pp. 162-171. El texto original está en el dominio público en su país de origen y en otros países y zonas donde el plazo de los derechos de autor es la vida del autor más 70 años o menos. Esta traducción se publica bajo los términos de la licencia Creative Commons Atribución-Compartir Igual.
Ludwig Wittgenstein
Algunas observaciones sobre la forma lógica
Toda proposición tiene un contenido y una forma. Nosotros adquirimos la imagen de la forma pura si abstraemos del significado de las palabras individuales, o símbolos (en la medida que tienen significados independientes). Esto es, si sustituimos variables por las constantes de la proposición. Las reglas de la sintaxis que son aplicadas a las constantes deben aplicarse también a las variables. Por sintaxis, en este sentido general de la palabra, me refiero a las reglas que nos dicen solo en qué conexiones una palabra tiene sentido, excluyendo así estructuras sin sentido. La sintaxis del lenguaje ordinario, como es bien conocido, no es muy adecuada a este propósito. No impide en todos los casos la construcción de pseudoproposiciones sin sentido (construcciones como “el rojo es más alto que el verde” o “lo Real, aunque es un en sí mismo, también debe ser capaz de convertirse en un para mí mismo”, etc.).
Si tratamos de analizar cualquier proposición dada nos daremos cuenta, en general, que son sumas lógicas, productos u otras funciones de verdad de proposiciones más simples. Pero nuestro análisis, si es llevado lo suficientemente lejos, debe llegar al punto donde alcanza formas proposicionales que no están a su vez compuestas por formas proposicionales más simples. Debemos finalmente llegar a la conexión definitiva de los términos, la conexión inmediata que no puede ser rota sin destruir la forma proposicional como tal. Las proposiciones que representan esta conexión definitiva de los términos las llamo, por B. Russell, proposiciones atómicas. Ellas, entonces, son el núcleo de todas las demás proposiciones, ellas contienen el material, y todo el resto es solo un desarrollo de este material. Son ellas las que tenemos que observar para hallar el objeto de las proposiciones. Es la tarea de la teoría del conocimiento encontrarlas y entender su construcción a partir de palabras o símbolos. Esta tarea es muy difícil, y la Filosofía apenas ha empezado a abordarla en ciertos puntos. ¿Qué método tenemos para abordarla? La idea es expresar en un simbolismo apropiado lo que en el lenguaje ordinario lleva a un sinfín de malentendidos. Esto es, donde el lenguaje ordinario oculta la estructura lógica, donde permite la formación de pseudoproposiciones, donde usa un término en una infinidad de significados diferentes, debemos reemplazarlo por un simbolismo que dé una imagen clara de la estructura lógica, excluya pseudoproposiciones y use sus términos sin ambigüedad. Ahora, solo podemos sustituir un simbolismo claro por el impreciso inspeccionando el fenómeno que queremos describir, tratando así de entender su multiplicidad lógica. Esto es, sólo podemos llegar al análisis correcto a través de, lo que puede ser llamado, la investigación lógica de los fenómenos mismos, esto es, en cierto sentido a posteriori, y no haciendo conjeturas sobre posibilidades a priori. Uno suele sentirse tentado a preguntar desde una óptica a priori: Qué, después de todo, pueden ser las únicas formas de proposiciones atómicas y contestar, por ejemplo, sujeto-predicado y relaciones proposicionales con dos o más términos, quizá, proposiciones que relacionan predicados y relaciones entre ellos, y así sucesivamente. Pero esto, creo, solamente es jugar con las palabras. Una forma atómica no puede ser prevista. Y sería sorprendente si el fenómeno real no tuviera nada más que enseñarnos sobre su estructura. A estas conjeturas sobre la estructura de las proposiciones atómicas somos llevados por nuestro lenguaje ordinario, que usa la estructura sujeto-predicado y la forma relacional. Pero esto en nuestro lenguaje es engañoso: Trataré de explicarlo con un símil. Imaginemos dos planos paralelos, I y II. En el plano I se dibujan figuras, por ejemplo, elipses y rectángulos de diferentes tamaños y formas, y nuestra es tarea producir imágenes de estas figuras en el plano II. Luego podemos imaginar dos maneras, entre otras, para hacer esto. Podemos, en primer lugar, establecer una ley de proyección—puede ser la de proyección ortogonal o cualquier otra—y luego proceder a proyectar todas las figuras de I a II, según esta ley. O, en segundo lugar, podemos proceder así: Establecemos la ley de que cada elipse en el plano I debe aparecer como un círculo en el plano II, y cada rectángulo como cuadrado en II. Tal forma de representación puede ser conveniente para nosotros si por alguna razón preferimos sólo dibujar círculos y cuadrados en el plano II. Por supuesto, de estas imágenes las formas exactas de las figuras originales del plano I no puedes ser inferidas inmediatamente. Solamente podemos saber a través de ellas que el original era una elipse o un rectángulo. Para conseguir la forma determinada del original en una sola instancia, tendríamos que saber el método individual por el cual, por ejemplo, una elipse particular es proyectada en el círculo ante mí. El caso del lenguaje ordinario es bastante análogo. Si los hechos de la realidad son los elipses y rectángulos del plano I, la estructura sujeto-predicado y las formas relacionales corresponden a los círculos y cuadrados del plano II. Estas formas son las reglas de nuestro lenguaje particular en el cual proyectamos en tantas maneras diferentes formas lógicas diferentes en tantas maneras. Y por esta razón no podemos sacar conclusiones—excepto unas muy vagas—del uso de estas reglas como la forma lógica real del fenómeno descrito. Formas como “Este artículo es aburrido”, “El clima está bien”, “Soy perezoso”, que no tienen nada que ver entre ellas, se presentan como proposiciones sujeto-predicado, esto es, aparentemente como proposiciones de la misma forma.
Si, ahora, tratamos de llegar a un análisis real, encontramos formas lógicas que poca similitud tienen con las reglas del lenguaje ordinario. Nos encontramos con las formas del espacio y el tiempo con todo el conjunto de la variedad espacial y objetos temporales, como colores, sonidos, etc., etc., con sus graduaciones, transiciones continuas y combinaciones en proporciones varias, todas las cuales no pueden ser captadas por nuestros medios ordinarios de expresión. Y aquí deseo hacer mi primera observación definitiva en el análisis lógico de los fenómenos reales: es por esto, que para su representación números (racionales e irracionales) deben entrar en la estructura de las proposiciones atómicas mismas. Ilustraré esto con un ejemplo. Imagine un sistema de ejes rectangulares, por así decirlo, cables cruzados, dibujados en nuestro campo de visión y una escala arbitraria fijada. Entonces es claro que podemos describir la forma y posición de cada parche de color en nuestro campo visual por medio de declaraciones de números que tengan su significado relativo al sistema de coordenadas y la unidad escogida. De nuevo, es claro que esta descripción tendrá la multiplicidad lógica correcta, y que una descripción que tenga menos multiplicidad no servirá. Un simple ejemplo sería la representación de un parche P por la expresión “[6-9, 3-8]” y de una proposición sobre esta,
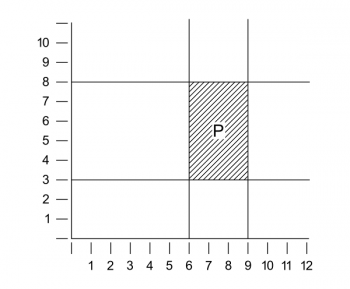
por ejemplo, P es rojo, por el símbolo “[6-9, 3-8] R”, donde “R” aún es un término sin analizar (“6-9” y “3-8” representan el intervalo continuo entre los respectivos números). Aquí el sistema de coordenadas es parte del modo de expresión; es parte del método de proyección por el cual la realidad es proyectada en nuestro simbolismo. La relación de un parche estando entre otros dos puede ser expresada análogamente por el uso de variables aparentes. No hace falta que diga que este análisis de ninguna manera pretende ser completo. No he hecho mención en él del tiempo, y el uso de espacio bidimensional no se justifica incluso en el caso de la visión monocular. Sólo deseo señalar la dirección en la que, creo, el análisis de los fenómenos visuales debe ir, y que en este análisis nos encontramos con formas lógicas bastante diferentes de aquellas que el lenguaje ordinario nos lleva a esperar. La aparición de números en las formas de las proposiciones atómicas es, en mi opinión no simplemente una característica de un simbolismo especial, sino una parte esencial y, por tanto, inescapable de la representación. Y los números tendrán que entrar en estas formas cuando—como solemos decir en lenguaje ordinario—estamos tratando con propiedades que admiten gradación, por ejemplo, propiedades como la longitud de un intervalo, la altura de un sonido, el brillo o rojez de un tono de color, etc. Es una característica de estas propiedades que un grado de ellas excluye a todos los demás. Un tono de color no puede simultáneamente tener dos grados diferentes de brillo o rojez, un tono no puede tener dos fuerzas diferentes, etc. Y el punto importante aquí es que estas observaciones no expresan una experiencia, sino que en cierto sentido son tautologías. Cada uno de nosotros sabe esto en la vida ordinaria. Si alguien nos pregunta “¿Qué temperatura hace afuera?” y contestamos “Ochenta grados”, y ahora nos preguntara de nuevo, “¿Y hacen noventa grados?” nosotros deberíamos contestar, “Te dije que hacían ochenta”. Tomamos la afirmación de grado (de la temperatura, por ejemplo) como una descripción completa que no requiere suplementación. Así, cuando nos preguntan, decimos qué hora es y no por aparte qué hora no es.
Uno podría pensar—y eso pensaba hasta hace no mucho—que una afirmación expresando un grado de cualidad podría ser analizada en un producto lógico de afirmaciones individuales de cantidad y una afirmación suplementaria que lo complete. Siendo que podría describir los contenidos de mi bolsillo diciendo “Contiene un penique, un centavo, dos llaves y nada más”. Este “y nada más” es la afirmación suplementaria que completa la descripción. Pero esto no sirve como análisis de una afirmación de grado. Llamemos a la unidad de, por ejemplo, brillo b y que E(b) sea la afirmación que la entidad E posee ese brillo, entonces la proposición E(2b), que dice que E tiene dos grados de brillo, debería ser analizable en el producto lógico E(b) & E(b), pero esto es igual a E(b); si, por otra parte, tratásemos de distinguir entre unidades y consecuentemente escribir E(2b) = E(b’) & E(b’’), asumiríamos dos unidades diferentes de brillo; y entonces, si una entidad posee una unidad, surge la pregunta, cuál de las dos— b’ o b’’— es; lo que obviamente es absurdo.
Sostengo que una afirmación que atribuye grado a una cualidad no puede analizarse más a fondo, y, además, que la relación de diferencia del grado es una relación interna y que es por tanto representada por una relación interna entre afirmaciones que atribuyen diferentes grados. Esto es, la afirmación atómica debe tener la misma multiplicidad del grado que atribuye, de donde se sigue que los números deben entrar a las formas de las proposiciones atómicas. La exclusión mutua de afirmaciones de grado no analizables contradice una opinión que fue publicada por mí varios años atrás y que necesitaba que las proposiciones atómicas no se excluyeran unas a otras. Digo aquí deliberadamente “excluir” y no “contradecir”, pues hay una diferencia entre estas dos nociones, y las proposiciones atómicas, aunque no pueden contradecir, pueden excluir unas a otras. Trataré de explicar esto. Hay funciones que pueden dar a una proposición verdadera sólo un valor de su argumento porque—si me puedo expresar así—sólo hay espacio en ellas para uno. Por ejemplo, una proposición que afirme la existencia del color R en un tiempo T en un espacio P de nuestro campo visual. Escribiré esta proposición “RPT” y abstraeré por el momento de cualquier consideración de cómo una afirmación así se debe analizar más a fondo. “BPT”, entonces, dice que el color B está en el lugar P en el tiempo T, y será claro para la mayoría de nosotros aquí, y para todos en nuestra vida ordinaria, que “RPT & BPT” es algún tipo de contradicción (y no simplemente una proposición falsa). Ahora, si las afirmaciones de grado fueran analizables—como solía pensar—podríamos explicar esta contradicción diciendo que el color R contiene todos los grados de R y ninguno de B y que el color B contiene todos los grados de B y ninguno de R. Pero de lo anterior se sigue que ningún análisis puede eliminar afirmaciones de grado. ¿Cómo, entonces, opera la exclusión mutua de RPT y BPT? Creo que consiste en el hecho de que tanto RPT como BPT son, en cierto sentido, completas. Eso que corresponde en la realidad a la función “( )PT” solamente deja espacio para una entidad—en el mismo sentido, de hecho, en el que decimos que sólo hay espacio para una persona en una silla. Nuestro simbolismo, que nos permite formar el signo del producto lógico de “RPT” y “BPT” no nos da una representación correcta de la realidad.
He dicho en otro lado que una proposición “llega hasta la realidad”, y con esto quiero decir que las formas de las entidades están contenidas en la forma de la proposición que es sobre estas entidades. Para la oración, junto con el modo de proyección que proyecta la realidad en la oración, determina la forma lógica de las entidades, al igual que en nuestro símil una imagen en el plano II, junto con su modo de proyección, determina la forma de la figura en el plano I. Esta observación, creo, nos da la clave para la explicación de la exclusión mutua de RPT y BPT. Pues si la proposición contiene la forma de la entidad de la que trata, entonces es posible que dos proposiciones colisionen en esta misma forma. Las proposiciones, “Brown ahora se sienta en esta silla” y “Jones ahora se sienta en esta silla” cada una, en un sentido, intenta poner a su término del sujeto en la silla. Pero el producto lógico de estas proposiciones los pondrá a ambos a la vez, y esto lleva a una colisión, una exclusión mutua de estos términos. ¿Cómo se representa a si misma esta exclusión en simbolismo? Podemos escribir el producto lógico de dos proposiciones, p y q, de esta manera:—
| p | q | |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
¿Qué pasa si estas dos proposiciones son RPT y BPT? En este caso, la fila superior “TTT” debe desaparecer, pues representa una combinación imposible. Las posibilidades reales aquí son—
| R P T | B P T |
| T | F |
| F | T |
| F | F |
Esto es, no hay producto lógico de RPT y BPT en el primer sentido, y aquí se encuentra la exclusión en lugar de una contradicción. La contradicción, si existiese, se escribiría—
| R P T | B P T | |
| T | T | F |
| T | F | F |
| F | T | F |
| F | F | F |
pero esto carece de sentido, pues la línea superior, “TTF”, da a la proposición una multiplicidad lógica superior a aquella de las posibilidades reales. Esto es, por supuesto, una deficiencia en nuestra notación que no previene la formación de construcciones sin sentido como esta, y una notación perfecta tendría que excluir estas construcciones por medio de reglas definidas de sintaxis. Estas tendrán que decirnos que, en el caso de ciertos tipos de proposiciones atómicas descritas en términos de características simbólicas definidas, algunas combinaciones de T y F deben ser dejadas afuera. Tales reglas, sin embargo, no pueden ser establecidas hasta que hayamos llegado al análisis definitivo de los fenómenos en cuestión. Esto, como todos sabemos, aún no ha sido logrado.
