Brown Book: Difference between revisions
No edit summary |
No edit summary |
||
| Line 129: | Line 129: | ||
Schemes of this kind can be adjoined to our tables, as rules for reading them. Could not these rules again be explained by further rules? Certainly. On the other hand, is a rule incompletely explained if no rule for its usage has been given? | Schemes of this kind can be adjoined to our tables, as rules for reading them. Could not these rules again be explained by further rules? Certainly. On the other hand, is a rule incompletely explained if no rule for its usage has been given? | ||
We introduce into our language-games the endless series of numerals. But how is this done? Obviously the analogy between this process & that of introducing a series of twenty numerals is not the same as that between introducing a series of twenty numerals and introducing a series of ten numerals. Suppose that our game was like 2) but played with the endless series of numerals. The difference between it & 2) would not be just that more numerals were used. That is to say, suppose that as a matter of fact in playing the game we had actually made use of, say, 155 numerals, the game we play would not be that which could be described by saying that we played the game 2), only with 155 instead of 10 numerals. But what does the difference consist in? (The difference would seem to be almost | We introduce into our language-games the endless series of numerals. But how is this done? Obviously the analogy between this process & that of introducing a series of twenty numerals is not the same as that between introducing a series of twenty numerals and introducing a series of ten numerals. Suppose that our game was like 2) but played with the endless series of numerals. The difference between it & 2) would not be just that more numerals were used. That is to say, suppose that as a matter of fact in playing the game we had actually made use of, say, 155 numerals, the game we play would not be that which could be described by saying that we played the game 2), only with 155 instead of 10 numerals. But what does the difference consist in? (The difference would seem to be almost {{BBB TS reference|Ts-310,23}} one of the spirit in which the games are played.) The difference between games can lie say in the number of the counters used, in the number of squares of the playing board, or in the fact that we use squares in one case & hexagons in the other, & such like. Now the difference between the finite and infinite game does not seem to lie in the material tools of the game; for we should be inclined to say that infinity can't be expressed in them, that is, that we can only conceive of it in our thoughts & hence that it is in these thoughts that the finite and infinite game must be distinguished. (It is queer though that these thoughts should be capable of being expressed in signs.) Let us consider two games. They are both played with cards carrying numbers, and the highest number takes the trick. | ||
{{parBB|22}} One game is played with a fixed number of such cards, say 32. In the other game we are under certain circumstances allowed to increase the number of cards to as many as we like, by cutting pieces of paper and writing numbers on them. We will call the first of these games bounded, the second unbounded. Suppose a hand of the second game was played & the number of cards actually used was 32. What is the difference in this case between playing a hand ''a'') of the unbounded game & playing a hand ''b'') of the bounded game? | |||
{{parBB|22}} One game is played with a fixed number of such cards, say 32. In the other game we are under certain circumstances allowed to increase the number of cards to as many as we like, by cutting pieces of paper and writing numbers on them. We will call the first of these games bounded, the second unbounded. Suppose a hand of the second game was played & the number of cards actually used was 32. What is the difference in this case between playing a hand a) of the unbounded game & playing a hand b) of the bounded game? | |||
The difference will not be that between a hand of a bounded game with 32 cards and a hand of a bounded game with a greater number of cards. The number of cards used was, we said, the same. But there will be differences of another kind, e.g., the bounded game is played with a normal pack of cards, the unbounded game with a large supply of blank cards & pencils. | The difference will not be that between a hand of a bounded game with 32 cards and a hand of a bounded game with a greater number of cards. The number of cards used was, we said, the same. But there will be differences of another kind, e.g., the bounded game is played with a normal pack of cards, the unbounded game with a large supply of blank cards & pencils. | ||
{{BBB TS reference|Ts-310,24}} The unbounded game is opened with the question, “How high shall we go?” If the players look up the rules of this game in a book of rules, they will find the phrase “& so on” or “& so on ad inf.” at the end of certain series of rules. So the difference between the two hands a) & b) lies in the tools we use, though admittedly not in the cards they are played with. But this difference seems trivial and not the essential difference between the games. We feel that there must be a big & essential difference somewhere. But if you look closely at what happens when the hands are played, you find that you can only detect a number of differences in details, each of which would seem inessential. The acts, e.g., of dealing & playing the cards may in both cases be identical. In the course of playing the hand a), the players may have considered making up more cards, & again discarded the idea. But what was it like to consider this? It could be some such process as saying to themselves or aloud, “I wonder whether I should make up another card”. Again, no such consideration may have entered the minds of the players. It is possible that the whole difference in the events of a hand of the bounded, and a hand of the unbounded game lay in what was said before the game started, e.g., “Let's play the bounded game”. | {{BBB TS reference|Ts-310,24}} The unbounded game is opened with the question, “How high shall we go?” If the players look up the rules of this game in a book of rules, they will find the phrase “& so on” or “& so on ad inf.” at the end of certain series of rules. So the difference between the two hands ''a'') & ''b'') lies in the tools we use, though admittedly not in the cards they are played with. But this difference seems trivial and not the essential difference between the games. We feel that there must be a big & essential difference somewhere. But if you look closely at what happens when the hands are played, you find that you can only detect a number of differences in details, each of which would seem inessential. The acts, e.g., of dealing & playing the cards ''may'' in both cases be identical. In the course of playing the hand ''a''), the players may have considered making up more cards, & again discarded the idea. But what was it like to consider this? It could be some such process as saying to themselves or aloud, “I wonder whether I should make up another card”. Again, no such consideration may have entered the minds of the players. It is possible that the whole difference in the events of a hand of the bounded, and a hand of the unbounded game lay in what was said before the game started, e.g., “Let's play the bounded game”. | ||
“But isn't it correct to say that hands of the two different games belong to two different systems?” Certainly. Only the facts which we are referring to by saying that they belong to different systems are much more complex than we might expect them to be. | “But isn't it correct to say that hands of the two different games belong to two different systems?” Certainly. Only the facts which we are referring to by saying that they belong to different systems are much more complex than we might expect them to be. | ||
Let us now compare language-games of which we should say | Let us now compare language-games of which we should say {{BBB TS reference|Ts-310,25}} that they are played with a limited set of numerals with language-games of which we should say that they are played with the endless series of numerals. | ||
{{BBB TS reference|Ts-310,25}} that they are played with a limited set of numerals with language-games of which we should say that they are played with the endless series of numerals. | |||
{{parBB|23}} Like 2) A orders B to bring him a number of building stones. The numerals are the signs “1”, “2”, etc. … “9”, each written on a card. A has a set of these cards and gives B the order by shewing him one of the set & calling out one of the words, “slab”, “column”, etc. | {{parBB|23}} Like 2) A orders B to bring him a number of building stones. The numerals are the signs “1”, “2”, etc. … “9”, each written on a card. A has a set of these cards and gives B the order by shewing him one of the set & calling out one of the words, “slab”, “column”, etc. | ||
| Line 159: | Line 153: | ||
{{parBB|28}} Like 26). If the heap contains n plates, n being more than 20 but less than 40, B moves n-20 beads, shews A the abacus thus set, & claps his hand once. | {{parBB|28}} Like 26). If the heap contains n plates, n being more than 20 but less than 40, B moves n-20 beads, shews A the abacus thus set, & claps his hand once. | ||
{{parBB|29}} A & B use the numerals of the decimal system (written or spoken) up to 20. The child learning this language learns these | {{parBB|29}} A & B use the numerals of the decimal system (written or spoken) up to 20. The child learning this language learns these {{BBB TS reference|Ts-310,26}} numerals by heart, etc., as in 2). | ||
{{BBB TS reference|Ts-310,26}} numerals by heart, etc., as in 2). | |||
{{parBB|30}} A certain tribe has a language of the kind 2). The numerals used are those of our decimal system. No one numeral used can be observed to play the predominant role of the last numeral in some of the above games (27), 28)). (One is tempted to continue this sentence by saying, “although there is of course a highest numeral actually used”). The children of the tribe learn the numerals in this way: They are taught the signs from 1 to 20 as in 2) and to count rows of beads of no more than 20 on being ordered, “Count these”. When in counting the pupil arrives at the numeral 20, one makes a gesture suggestive of “Go on”, upon which the child says (in most cases at any rate) “21”. Analogously, the children are made to count to 22 & to higher numbers, no particular number playing in these exercises the predominant role of a last one. The last stage of the training is that the child is ordered to count a group of objects, well above 20, without the suggestive gesture being used to help the child over the numeral 20. If a child does not respond to the suggestive gesture, it is separated from the others and treated as a lunatic. | {{parBB|30}} A certain tribe has a language of the kind 2). The numerals used are those of our decimal system. No one numeral used can be observed to play the predominant role of the last numeral in some of the above games (27), 28)). (One is tempted to continue this sentence by saying, “although there is of course a highest numeral actually used”). The children of the tribe learn the numerals in this way: They are taught the signs from 1 to 20 as in 2) and to count rows of beads of no more than 20 on being ordered, “Count these”. When in counting the pupil arrives at the numeral 20, one makes a gesture suggestive of “Go on”, upon which the child says (in most cases at any rate) “21”. Analogously, the children are made to count to 22 & to higher numbers, no particular number playing in these exercises the predominant role of a last one. The last stage of the training is that the child is ordered to count a group of objects, well above 20, without the suggestive gesture being used to help the child over the numeral 20. If a child does not respond to the suggestive gesture, it is separated from the others and treated as a lunatic. | ||
{{parBB|31}} Another tribe. Its language is like that in 30). The highest numeral observed in use is 159. In the life of this tribe the numeral 159 plays a peculiar role. Supposing I said, “They treat this number as their highest”, – – but what does this mean? Could we answer: “They just say that it is the highest”? ‒ ‒ They say certain words, but how do we know what they mean by them? A criterion for what they mean would be the occasions | {{parBB|31}} Another tribe. Its language is like that in 30). The highest numeral observed in use is 159. In the life of this tribe the numeral 159 plays a peculiar role. Supposing I said, “They treat this number as their highest”, – – but what does this mean? Could we answer: “They just say that it is the highest”? ‒ ‒ They say certain words, but how do we know what they mean by them? A criterion for what they mean would be the occasions {{BBB TS reference|Ts-310,27}} on which the word we are inclined to translate into our word “highest” is used, the role, we might say, which we observe this word to play in the life of the tribe. In fact we could easily imagine the numeral 159 to be used on such occasions, in connection with such gestures and forms of behaviour as would make us say that this numeral plays the role of an unsurmountable limit, even if the tribe had no word corresponding to our “highest”, and the criteria for numeral 159 being the highest numeral did not consist of anything that was ''said'' about the numeral. | ||
{{BBB TS reference|Ts-310,27}} on which the word we are inclined to translate into our word “highest” is used, the role, we might say, which we observe this word to play in the life of the tribe. In fact we could easily imagine the numeral 159 to be used on such occasions, in connection with such gestures and forms of behaviour as would make us say that this numeral plays the role of an unsurmountable limit, even if the tribe had no word corresponding to our “highest”, and the criteria for numeral 159 being the highest numeral did not consist of anything that was said about the numeral. | |||
{{ | {{parBB|32}} A tribe has two systems of counting. People learned to count with the alphabet from A to Z and also with the decimal system as in 30). If a man is to count objects with the first system, he is ordered to count “''in the closed way''”, in the second case, “''in the open way''”; & the tribe uses the words “closed” & “open” also for a closed and open door. | ||
{{BBB TS reference|Ts-310,29}} “transcendent” rests on a misunderstanding.) | (Remarks: 23) is limited in an obvious way by the set of cards. 24): Note analogy and lack of analogy between the ''limited supply'' of cards in 23) & of words in our memory in 24). Observe that the limitation in 26) on the one hand lies in the ''tool'' (the abacus of 20 beads) & its usage in our game, on the other hand (in a totally different way) in the fact that in the actual practice of playing the game no more than 20 objects are ever to be counted. In 27) that latter kind of limitation was absent, but the large bead rather stressed the limitation of our means. Is 28) a limited or an unlimited game? The practice we have described gives the limit 40. We are inclined to say this game “has it in it” to be continued indefinitely, but remember {{BBB TS reference|Ts-310,28}} that we could also have construed the preceding games as beginnings of a system. In 29) the systematic aspect of the numerals used is even more conspicuous than in 28). One might say that there was no limitation imposed by the tools of this game, if it were not for the remark that the numerals up to 20 are learnt by heart. This suggests the idea that the child is not taught to “''understand''” the system which we see in the decimal notation. Of the tribe in 30) we should certainly say that they are trained to construct numerals indefinitely, that the arithmetic of their language is not a finite one, that their series of numbers has no end. (It is just in such a case when numerals are constructed “indefinitely” that we say that people have the infinite series of numbers.) 31) might shew you what a vast variety of cases can be imagined in which we should be inclined to say that the arithmetic of the tribe deals with a finite series of numbers, even in spite of the fact that the way in which the children are trained in the use of numerals suggests no upper limit. In 32) the terms “closed” & “open” (which could by a slight variation of the example be replaced by “limited” and “unlimited”) are introduced into the language of the tribe itself. Introduced in that simple and clearly circumscribed game, there is of course nothing mysterious about the use of the word “open”. But this word corresponds to our “infinite”, & the games we play with the latter differ from 31) only by being vastly more complicated. In other words, our use of the word “infinite” is just as ''straight forward'' as that of “open” in 31 || 32?), and our idea that its meaning is {{BBB TS reference|Ts-310,29}} “transcendent” rests on a misunderstanding.) | ||
We might say roughly that the unlimited cases are characterized by this: that they are not played with a definite supply of numerals, but instead with a system for constructing numerals (indefinitely). When we say that someone has been supplied with a system for constructing numerals, we generally think of either of three things: a) of giving him a training similar to that described in 30), which, experience teaches us, will make him pass tests of the kind mentioned there; b) of creating a disposition in the same man's mind, or brain, to react in that way; c) of supplying him with a general rule for the construction of numerals. | We might say roughly that the unlimited cases are characterized by this: that they are not played with a ''definite supply'' of numerals, but instead with a ''system'' for constructing numerals (indefinitely). When we say that someone has been supplied with a system for constructing numerals, we generally think of either of three things: a) of giving him a ''training'' similar to that described in 30), which, experience teaches us, will make him pass tests of the kind mentioned there; b) of creating a ''disposition'' in the same man's mind, or brain, to react in that way; c) of supplying him with a ''general rule'' for the construction of numerals. | ||
What do we call a rule? Consider this example: | What do we call a rule? Consider this example: | ||
Revision as of 20:52, 3 February 2021
Part I
Template:BBB TS reference Augustine, in describing his learning of language, says that he was taught to speak by learning the names of things. It is clear that whoever says this has in mind the way in which a child learns such words as “man”, “sugar”, “table”, etc. He does not primarily think of such words as “today”, “not”, “but”, “perhaps”.
Suppose a man described a game of chess, without mentioning the existence and operations of the pawns. His description of the game as a natural phenomenon will be incomplete. On the other hand we may say that he has completely described a simpler game. In this sense we can say that Augustine's description of learning the language was correct for a simpler language than ours. Imagine this language: –
). Its function is the communication between a builder A & his man B. B has to reach A building stones. There are cubes, bricks, slabs, beams, columns. The language consists of the words “cube”, “brick”, “slab”, “column”. A calls out one of these words, upon which B brings a stone of a certain shape. Let us imagine a society in which this is the only system of language. The child learns this language from the grown-ups by being trained to its use. I am using the word “trained” in a way strictly analogous to that in which we talk of an animal being trained to do certain things. It is done by means of example, reward, punishment, and such like. Part of this training is that we point to a building stone, direct the attention of the child towards it, & pronounce a word. I will call this procedure demonstrative teaching of words. In the actual Template:BBB TS reference use of this language, one man calls out the words as orders, the other acts according to them. But learning and teaching this language will contain this procedure: The child just “names” things, that is, he pronounces the words of the language when the teacher points to the things. In fact, there will be a still simpler exercise: The child repeats words which the teacher pronounces.
(Note: Objection: The word “brick” in language 1) has not the meaning which it has in our language. ‒ ‒ This is true if it means that in our language there are usages of the word “brick!” different from our usages of this word in language 1). But don't we sometimes use the word “brick!” in just this way? Or should we say that when we use it, it is an elliptical sentence, a shorthand for “Bring me a brick”? Is it right to say that if we say “brick!” we mean “Bring me a brick”? Why should I translate the expression “brick!” into the expression, “Bring me a brick”? And if they are synonymous, why shouldn't I say: If he says “brick!” he means “brick!” … ? Or: Why shouldn't he be able to mean just “brick!” if he is able to mean “Bring me a brick”, unless you wish to assert that while he says aloud “brick!” he as a matter of fact always says in his mind, to himself, “Bring me a brick”? But what reason could we have to assert this? Suppose someone asked: If a man gives the order, “Bring me a brick”, must he mean it as four words, or can't he mean it as one composite word synonymous with the one word “brick!”? One is tempted to answer: He means all four words if in his language he uses that sentence in contrast with other Template:BBB TS reference sentences in which these words are used, such as, for instance, “Take these two bricks away”. But what if I asked, “But how is his sentence contrasted with these others? Must he have thought them simultaneously, or shortly before or after, or is it sufficient that he should have one time learnt them, etc.?” When we have asked ourselves this question, it appears that it is irrelevant which of these alternatives is the case. And we are inclined to say that all that is really relevant is that these contrasts should exist in the system of language which he is using, and that they need not in any sense be present in his mind when he utters his sentence. Now compare this conclusion with our original question. When we asked it, we seemed to ask a question about the state of mind of the man who says the sentence, whereas the idea of meaning which we arrived at in the end was not that of a state of mind. We think of the meaning of signs sometimes as states of mind of the man using them, sometimes as the role which these signs are playing in a system of language.The connection between these two ideas is that the mental experiences which accompany the use of a sign undoubtedly are caused by our usage of the sign in a particular system of language. William James speaks of specific feelings accompanying the use of such words as “&”, “if”, “or”. And there is no doubt that at least certain gestures are often connected with such words, as a collecting gesture with “and”, & a dismissing gesture with “not”. And there obviously are visual and muscular sensations connected with these gestures. On the other hand it is clear enough that these sensations do not accompany every use of the word “not”, and “&”. If in some language the word “but” meant what “not” means in English, it is clear that we should not compare the meanings of these two Template:BBB TS reference words by comparing the sensations which they produce. Ask yourself what means we have of finding out the feelings which they produce in different people and on different occasions. Ask yourself: “When I said, ‘Give me an apple & a pear, & leave the room’, had I the same feeling when I pronounced the two words ‘&’?” But we do not deny that the people who use the word “but” as “not” is used in English will broadly speaking have similar sensations accompanying the word “but” as the English have when they use “not”. And the word “but” in the two languages will on the whole be accompanied by different sets of experiences.)
). Let us now look at an extension of language 1). The builder's man knows by heart the series of words from one to ten. On being given the order, “Five slabs!”, he goes to where the slabs are kept, says the words from one to five, takes up a plate for each word, & carries them to the builder. Here both the parties use the language by speaking the words. Learning the numerals by heart will be one of the essential features of learning this language. The use of the numerals will again be taught demonstratively. But now the same word, e.g., “three”, will be taught either by pointing to slabs, or to bricks, or to columns, etc. And on the other hand, different numerals, will be taught by pointing to groups of stones of the same shape.
(Remark: We stressed the importance of learning the series of numerals by heart because there was no feature comparable to this in the learning of language 1). And this shews us that by introducing numerals we have introduced an entirely different
Template:BBB TS reference kind of instrument into our language. The difference of kind is much more obvious when we contemplate such a simple example than when we look at our ordinary language with innumerable kinds of words all looking more or less alike when they stand in the dictionary. ‒ ‒
What have the demonstrative explanations of the numerals in common with those of the words “slab”, “column”, etc. except a gesture and pronouncing the words? The way such a gesture is used in the two cases is different. This difference is blurred if one says, “In one case we point to a shape, in the other we point to a number”. The difference becomes obvious and clear only when we contemplate a complete example (i.e., the example of a language completely worked out in detail).)
). Let us introduce a new instrument of communication, – – a proper name. This is given to a particular object (a particular building stone) by pointing to it and pronouncing the name. If A calls the name, B brings the object. The demonstrative teaching of a proper name is different again from the demonstrative teaching in the cases 1) & 2).
(Remark: This difference does not lie, however, in the act of pointing and pronouncing the word or in any mental act (meaning)﹖ accompanying it, but in the role which the demonstration (pointing & pronouncing) plays in the whole training and in the use which is made of it in the practice of communication by means of this language. One might think that the difference could be described by saying that in the different cases we point to different kinds of objects. But suppose I point with Template:BBB TS reference my hand to a blue jersey. How does pointing to its colour differ from pointing to its shape? ‒ ‒ We are inclined to say the difference is that we mean something different in the two cases. And “meaning” here is to be some sort of process taking place while we point. What particularly tempts us to this view is that a man on being asked whether he pointed to the colour or the shape is, at least in most cases, able to answer this & to be certain that his answer is correct. If on the other hand, we look for two such characteristic mental acts as meaning the colour and meaning the shape, etc., we aren't able to find any, or at least none which must always accompany pointing to colour, pointing to shape, respectively. We have only a rough idea of what it means to concentrate one's attention on the colour as opposed to the shape, or vice versa. The difference one might say does not lie in the act of demonstration, but rather in the surrounding of that act in the use of the language.)
). On being ordered “This slab!”, B brings the plate to which A points. On being ordered, “Plate, there!”, he carries a plate to the place indicated. Is the word “there” taught demonstratively? Yes & no! When a person is trained in the use of the word “there”, the teacher will in training him make the pointing gesture and pronounce the word “there”. But should we say that thereby he gives a place the name “there”? Remember that the pointing gesture in this case is part of the practice of communication itself.
(Remark: It has been suggested that such words as “there”, Template:BBB TS reference “here”, “now”, “this” are the “real proper names” as opposed to what in ordinary life we call proper names, & in the view I am referring to, can only be called so crudely. There is a widespread tendency to regard what in ordinary life is called a proper name only as a rough approximation of what ideally could be called so. Compare Russell's idea of the “individual”. He talks of individuals as the ultimate constituents of reality, but says that it is difficult to say which things are individuals. The idea is that further analysis has to reveal this. We, on the other hand, introduced the idea of a proper name in a language in which it was applied to what in ordinary life we call “objects”, “things” (“building stones”).
– – “What does the word ‘exactness’ mean? Is it real exactness if you are supposed to come to tea at 4.30 and come when a good clock strikes 4.30? Or would it only be exactness if you began to open the door at the moment the clock begins to strike? But how is this moment to be defined and how is “beginning to open the door” to be defined? Would it be correct to say, ‘It is difficult to say what real exactness is, for all we know is only rough approximations’?”)
). Question and answer: A asks, “How many plates?” B counts them and answers with the numeral.
Systems of communication as for instance 1), 2), 3), 4), 5) we shall call “language-games”. They are more or less akin to what in ordinary language we call games. Children are taught their native language by means of such games, and here they even have the entertaining character of games. We are not, Template:BBB TS reference however, regarding the language-games which we describe as incomplete parts of a language, but as languages complete in themselves, as complete systems of human communication. To keep this point of view in mind, it very often is useful to imagine such a simple language to be the entire system of communication of a tribe in a primitive state of society. Think of primitive arithmetics of such tribes.
When the boy or grown-up learns what one might call special technical languages, e.g., the use of charts and diagrams, descriptive geometry, chemical symbolism, etc., he learns more language-games. (Remark: The picture we have of the language of the grown-up is that of a nebulous mass of language, his mother tongue, surrounded by discreet and more or less clear cut language games, the technical languages.)
). Asking for the name: we introduce new forms of building stones. B points to one of them & asks, “What is this?”; A answers, “This is a … ”. Later on A calls out this new word, say “arch”, & B brings the stone. The words, “This is a … ” together with the pointing gesture we shall call ostensive explanation or ostensive definition. In case 6) a generic name was explained, in actual fact, the name of a shape. But we can ask analogously for the proper name of a particular object, for the name of a colour, of a number || numeral, of a direction.
(Remark: Our use of expressions like “names of numbers”, “names of colours”, “names of materials”, “names of nations” may spring from two different sources. a) One is that we might imagine the functions of proper names, numerals, words for colours, Template:BBB TS reference etc. to be much more alike than they actually are. If we do so we are tempted to think that the function of every word is more or less like the function of a proper name of a person, or such generic names as “table”, “chair”, “door”, etc. The b) second source is this, that if we see how fundamentally different the functions of such words as “table”, “chair”, etc. are from those of proper names, and how different from either the functions of, say, the names of colours, we see no reason why we shouldn't speak of names of numbers or names of directions either, not by way of saying some such thing as “numbers and directions are just different forms of objects”, but rather by way of stressing the analogy which lies in the lack of analogy between the functions of the words “chair” & “Jack” on the one hand, & “east” and “Jack” on the other hand.)
). B has a table in which written signs are placed opposite to pictures of objects (say, a table, a chair, a tea-cup, etc.). A writes one of the signs, B looks for it in the table, looks or points with his finger from the written sign to the picture opposite, & fetches the object which the picture represents.
Let us now look at the different kinds of signs which we have introduced. First let us distinguish between sentences and words. A sentence I will call every complete sign in a language-game, its constituent signs are words. (This is merely a rough and general remark about the way I will use the words “proposition” and “word”). A proposition may consist of only one word. In 1) the signs “brick!”, “column!” are the sentences. In 2) a sentence consists of two words. According Template:BBB TS reference to the role which propositions play in a language-game, we distinguish between orders, questions, explanations, descriptions, & so on.
). If in a language-game similar to 1) A calls out an order: “slab, column, brick!” which is obeyed by B by bringing a slab, a column & a brick, we might here talk of three propositions, or of one only. If on the other hand,
). the order of words shews B the order in which to bring the building stones, we shall say that A calls out a proposition consisting of three words. If the command in this case took the form, “Slab, then column, then brick!” we should say that it consisted of four words (not of five). Amongst the words we see groups of words with similar functions. We can easily see a similarity in the use of the words “one”, “two”, “three”, etc. & again one in the use of “slab”, “column” & “brick”, etc., & thus we distinguish parts of speech. In 8) all words of the proposition belonged to the same part of speech.
). The order in which B had to bring the stones in 9) could have been indicated by the use of the ordinals thus: “Second, column; first, slab; third, brick!”. Here we have a case in which what was the function of the order of words in one language-game is the function of particular words in another.
Reflections such as the preceding will shew us the infinite variety of the functions of words in propositions, and it is curious to compare what we see in our examples with the simple & rigid rules which logicians give for the construction of propositions. If we group words together according to the similarity of their functions, thus distinguishing parts of speech, Template:BBB TS reference it is easy to see that many different ways of classification can be adopted. We could indeed easily imagine a reason for not classing the word “one” together with “two”, “three”, etc., as follows:
). Consider this variation of our language-game 2). Instead of calling out, “One slab!”, “One cube!”, etc., A just calls “slab!”, “cube!”, etc., the use of the other numerals being as described in 2). Suppose that a man accustomed to this form (11)) of communication was introduced to the use of the word “one” as described in 2). We can easily imagine that he would refuse to classify “one” with the numerals “2”, “3”, etc.
(Remark: Think of the reasons for and against classifying “0” with the other cardinals. “Are black and white colours?” In which cases would you be inclined to say so & which not? ‒ ‒ Words can in many ways be compared to chess men. Think of the several ways of distinguishing different kind of pieces in the game of chess (e.g., pawns & “officers”).
Remember the phrase, “two or more”.)
It is natural for us to call gestures, as those employed in 4), or pictures as in 7), elements or instruments of language. (We talk sometimes of a language of gestures.) The pictures in 7) & other instruments of language which have a similar function I shall call patterns. (This explanation, as others which we have given, is vague, and meant to be vague.) We may say that words and patterns have different kinds of functions. When we make use of a pattern we compare something with it, e.g., Template:BBB TS reference a chair with the picture of a chair. We did not compare a slab with the word “slab”. In introducing the distinction, “word, pattern”, the idea was not to set up a final logical duality. We have only singled out two characteristic kinds of instruments from the variety of instruments in our language. We shall call “one”, “two”, “three”, etc. words. If instead of these signs we used “-”, “--”, “---”, “----”, we might call these patterns. Suppose in a language the numerals were “one”, “one one”, “one one one”, etc., should we call “one” a word or a pattern? The same element may in one place be used as word & in another as pattern. A circle might be the name for an ellipse, or on the other hand a pattern with which the ellipse is to be compared by a particular method of projection. Consider also these two systems of expression:
). A gives B an order consisting of two written symbols, the first an irregularly shaped patch of a certain colour, say green, the second the drawn outline of a geometrical figure, say a circle. B brings an object of this outline and that colour, say a circular green object.
). A gives B an order consisting of one symbol, a geometrical figure painted a particular colour, say a green circle. B brings him a green circular object. In 12) patterns correspond to our names of colours and other patterns to our names of shape. The symbols in 13) cannot be regarded as combinations of two such elements. A word in inverted commas can be called a pattern. Thus in the sentence, “He said, ‘Go to hell’”, ‘Go to hell’ is a pattern of what he said. Compare these cases:
Template:BBB TS reference a) Someone says, “I whistled ![]() (whistling a tune)”; b) Someone writes, “I whistled ”. An onomatopoetic word like “rustling” may be called a pattern. We call a very great variety of processes “comparing an object with a pattern”. We comprise many kinds of symbols under the name “pattern”. In 7) B compares a picture in the table with the objects he has before him. But what does comparing a picture with the object consist in? Suppose the table shewed: a) a picture of a hammer, of pincers, of a saw, of a chisel; b) on the other hand, pictures of twenty different kinds of butterflies. Imagine what the comparison in these cases would consist in, & note the difference. Compare with these cases a third case c) where the pictures in the table represent building stones drawn to scale, & the comparing has to be done with ruler and compasses. Suppose that B's task is to bring a piece of cloth of the colour of the sample. How are the colours of sample and cloth to be compared? Imagine a series of different cases:
(whistling a tune)”; b) Someone writes, “I whistled ”. An onomatopoetic word like “rustling” may be called a pattern. We call a very great variety of processes “comparing an object with a pattern”. We comprise many kinds of symbols under the name “pattern”. In 7) B compares a picture in the table with the objects he has before him. But what does comparing a picture with the object consist in? Suppose the table shewed: a) a picture of a hammer, of pincers, of a saw, of a chisel; b) on the other hand, pictures of twenty different kinds of butterflies. Imagine what the comparison in these cases would consist in, & note the difference. Compare with these cases a third case c) where the pictures in the table represent building stones drawn to scale, & the comparing has to be done with ruler and compasses. Suppose that B's task is to bring a piece of cloth of the colour of the sample. How are the colours of sample and cloth to be compared? Imagine a series of different cases:
). A shews the sample to B, upon which B goes and fetches the material “from memory”.
). A gives B the sample, B looks from the sample to the materials on the shelves from which he has to choose.
). B lays the sample on each bolt of material & chooses that one which he can't distinguish from the sample, for which the difference between the sample & the material seems to vanish.
). Imagine on the other hand that the order has been, “Bring a material slightly darker than this sample”. In 14) I said that B fetches the material “from memory”, which is using a Template:BBB TS reference common form of expression. But what might happen in such a case of comparing “from memory” is of the greatest variety. Imagine a few instances:
). B has a memory image before his mind's eye when he goes for the material. He alternately looks at materials and recalls his image. He goes through this process with, say, five of the bolts, in some instances saying to himself, “Too dark”, in some instances saying to himself, “Too light”. At the fifth bolt he stops, says, “That's it”, & takes it from the shelf.
). No memory image is before B's eye. He looks at four bolts, shaking his head each time, feeling some sort of mental tension. On reaching the fifth bolt, this tension relaxes, he nods his head, & takes the bolt down.
). B goes to the shelf without a memory image, looks at five bolts one after the other, takes the fifth bolt from the shelf.
“But this can't be all comparing consists in”.
When we call these three preceding cases cases of comparing from memory, we feel that their description is in a sense unsatisfactory, or incomplete. We are inclined to say that the description has left out the essential feature of such a process & given us accessory features only. The essential feature it seems would be what one might call a specific experience of comparing & of recognizing. Now it is queer that on closely looking at cases of comparing, it is very easy to see a great number of activities and states of mind, all more or less characteristic Template:BBB TS reference of the act of comparing. This in fact is so, whether we speak of comparing from memory or of comparing by means of a sample before our eyes. We know a vast number of such processes, processes similar to each other in a vast number of different ways. We hold pieces whose colours we want to compare together or near each other for a longer or shorter period, look at them alternately or simultaneously, place them under different lights, say different things while we do so, have memory images, feelings of tension & relaxation, satisfaction & dissatisfaction, the various feelings of strain in and around our eyes accompanying prolonged gazing at the same object, & all possible combinations of these & many other experiences. The more such cases we observe & the closer we look at them, the more doubtful we feel about finding one particular mental experience characteristic of comparing. In fact, if after you had scrutinized a number of such closely, I admitted that there existed a peculiar mental experience which you might call the experience of comparing, & that if you insisted, I should be willing to adopt the word “comparing” only for cases in which this peculiar feeling had occurred, you would now feel that the assumption of such a peculiar experience had lost its point, because this experience was placed side by side with a vast number of other experiences which after we have scrutinized the cases seems to be that which really constitutes what connects all the cases of comparing. For the “specific experience” we had been looking for was meant to have played the role which has been assumed by the mass of experiences revealed to us by our Template:BBB TS reference scrutiny: We never wanted the specific experience to be just one among a number of more or less characteristic experiences. (One might say that there are two ways of looking at this matter, one as it were, at close quarters, the other as though from a distance and through the medium of a peculiar atmosphere.) In fact we have found that the use which we really make of the word “comparing” is different from that which looking at it from far away we were led to expect. We find that what connects all the cases of comparing is a vast number of overlapping similarities, and as soon as we see this, we feel no longer compelled to say that there must be some one feature common to them all. What ties the ship to the wharf is a rope, and the rope consists of fibres, but it does not get its strength from any fibre which runs through it from one end to the other, but from the fact that there is a vast number of fibres overlapping.
“But surely in case 14c) B acted entirely automatically. If all that happened was really what was described there, he did not know why he chose the bolt he did choose. He had no reason for choosing it. If he chose the right one, he did it as a machine might have done it”. Our first answer is that we did not deny that B in case 14c) had what we should call a personal experience, for we did not say that he didn't see the materials from which he chose or that which he chose, nor that he didn't have muscular and tactile sensations and such like while he did it. Now what would such a reason which justified his choice and made it non-automatic be like? (i.e.: What do we Template:BBB TS reference imagine it to be like?) I suppose we should say that the opposite of automatic comparing, as it were, the ideal case of conscious comparing, was that of having a clear memory image before our mind's eye or of seeing a real sample & of having a specific feeling of not being able to distinguish in a particular way between these samples and the material chosen. I suppose that this peculiar sensation is the reason, the justification, for the choice. This specific feeling, one might say, connects the two experiences of seeing the sample, on the one hand, and the material on the other. But if so, what connects this specific experience with either? We don't deny that such an experience might intervene. But looking at it as we did just now, the distinction between automatic and non-automatic appears no longer clear-cut and final as it did at first. We don't mean that this distinction loses its practical value in particular cases, e.g., if asked under particular circumstances, “Did you take this bolt from the shelf automatically, or did you think about it?”, we may be justified in saying that we did not act automatically and give as a reason || explanation we had looked at the material carefully, had tried to recall the memory image of the pattern, & had uttered to ourselves doubts and decisions. This may in the particular case be taken to distinguish automatic from non-automatic. In another case however we may distinguish between an automatic & a non-automatic way of the appearance of a memory image, and so on.
If our case 14c) troubles you, you may be inclined to say: “But why did he bring just this bolt of material? How has he Template:BBB TS reference recognized it as the right one? What by? ‒ ‒ If you ask “why”, do you ask for the cause or for the reason? If for the cause, it is easy enough to think up a physiological or psychological hypothesis which explains this choice under the given conditions. It is the task of the experimental sciences to test such hypotheses. If on the other hand you ask for a reason the answer is, “There need not have been a reason for the choice. A reason is a step preceding the step of the choice. But why should every step be preceded by another one?”
“But then B didn't really recognize the material as the right one”. ‒ ‒ You needn't reckon 14c) among the cases of recognizing, but if you have become aware of the fact that the processes which we call processes of recognition form a vast family with overlapping similarities, you will probably feel not disinclined to include 14c) in this family, too. ‒ ‒ “But doesn't B in this case lack the criterion by which he can recognize the material? In 14a), e.g., he had the memory image and he recognized the material he looked for by its agreement with the image”. ‒ ‒ But had he also a picture of this agreement before him, a picture with which he could compare the agreement between the pattern and the bolt to see whether it was the right one? And, on the other hand, couldn't he have been given such a picture? Suppose, e.g., that A wished B to remember that what was wanted was a bolt exactly like the sample, not, as perhaps in other cases, a material slightly darker than the pattern. Couldn't A in this case have given to B an example of the agreement required by giving him two pieces of the same colour (e.g., Template:BBB TS reference as a kind of reminder)? Is any such link between the order & its execution necessarily the last one? ‒ ‒ And if you say that in 14b) at least he had the relaxing of the tension by which to recognize the right material, had he to have an image of this relaxation about him to recognize it as that by which the right material was to be recognized? ‒ ‒
“But supposing B brings the bolt, as in 14c), & on comparing it with the pattern it turns out to be the wrong one?” ‒ ‒ But couldn't that have happened in all the other cases as well? Suppose in 14a) the bolt which B brought back was found not to match with the pattern. Wouldn't we in some such cases say that his memory image had changed, in others that the pattern or the material had changed, in others again that the light had changed? It is not difficult to invent cases, imagine circumstances, in which each of these judgements would be made. ‒ ‒ “But isn't there after all an essential difference between the cases 14a) & 14c)?”‒ ‒ Certainly! Just that pointed out in the description of these cases. ‒ ‒
In 1) B learnt to bring a building stone on hearing the word “column!” called out. We could imagine what happened in such a case to be this: In B's mind the word called out brought up an image of a column, say; the training had, as we should say, established this association. B takes up that building stone which conforms to his image. ‒ ‒ But was this necessarily what happened? If the training could bring it about that the idea or image – – automatically – – arose in B's mind, why shouldn't it bring about B's actions without the intervention of an image?
Template:BBB TS reference This would only come to a slight variation of the associative mechanism. Bear in mind that the image which is brought up by the word is not arrived at by a rational process (but if it is, this only pushes our argument further back), but that this case is strictly comparable with that of a mechanism in which a button is pressed and an indicator plate appears. In fact this sort of mechanism can be used instead of that of association.
Mental images of colours, shapes, sounds, etc. etc., which play a role in communication by means of language we put in the same category with patches of colour actually seen, sounds heard.
). The object of the training in the use of tables (as in 7)) may be not only to teach the use of one particular table, but it may be to enable the pupil to use or construct himself tables with new coordinations of written signs & pictures. Suppose the first table a person was trained to use contained the four words “hammer”, “pincers”, “saw”, “chisel” & the corresponding pictures. We might now add the picture of another object which the pupil had before him, say of a plane, & correlate with it the word “plane”. We shall make the correlation between this new picture and word as similar as possible to the correlations in the previous table. Thus we might add the new word and picture on the same sheet, and place the new word under the previous words and the new picture under the previous pictures. The pupil will now be encouraged to make use of the new picture and word without the special training which we gave him when we taught him to use the first table.
Template:BBB TS reference These acts of encouragement will be of various kinds, and many such acts will only be possible if the pupil responds, and responds in a particular way. Imagine the gestures, sounds, etc. of encouragement you use when you teach a dog to retrieve. Imagine on the other hand, that you tried to teach a cat to retrieve. As the cat will not respond to your encouragement, most of the acts of encouragement which you performed when you trained the dog are here out of the question.
). The pupil could also be trained to give things names of his own invention and to bring the objects when the names are called. He is, e.g., presented with a table on which he finds pictures of objects around him on one side and blank spaces on the other, and he plays the game by writing signs of his own invention opposite the pictures and reacting in the previous way when these signs are used as orders. Or else,
). the game may consist in B's constructing a table and obeying orders given in terms of this table. When the use of a table is taught, and the table consists, say, of two vertical columns, the left hand one containing the names, the right hand one the pictures, a name and a picture being correlated by standing on a horizontal line, an important feature of the training may be that which makes the pupil slide his finger from left to right, as it were the training to draw a series of horizontal lines, one below the other. Such training may help to make the transition from the first table to the new item.
Tables, ostensive definitions, & similar instruments I shall call rules, in accordance with ordinary usage. The use of a rule can be explained by a further rule.
Template:BBB TS reference ). Consider this example: We introduce different ways of reading tables. Each table consists of two columns of words & pictures, as above. In some cases they are to be read horizontally from left to right, i.e., according to the scheme:

In others according to such schemes as:
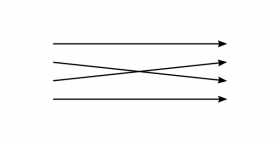
Or:
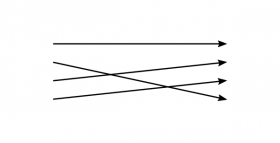
etc.
Schemes of this kind can be adjoined to our tables, as rules for reading them. Could not these rules again be explained by further rules? Certainly. On the other hand, is a rule incompletely explained if no rule for its usage has been given?
We introduce into our language-games the endless series of numerals. But how is this done? Obviously the analogy between this process & that of introducing a series of twenty numerals is not the same as that between introducing a series of twenty numerals and introducing a series of ten numerals. Suppose that our game was like 2) but played with the endless series of numerals. The difference between it & 2) would not be just that more numerals were used. That is to say, suppose that as a matter of fact in playing the game we had actually made use of, say, 155 numerals, the game we play would not be that which could be described by saying that we played the game 2), only with 155 instead of 10 numerals. But what does the difference consist in? (The difference would seem to be almost Template:BBB TS reference one of the spirit in which the games are played.) The difference between games can lie say in the number of the counters used, in the number of squares of the playing board, or in the fact that we use squares in one case & hexagons in the other, & such like. Now the difference between the finite and infinite game does not seem to lie in the material tools of the game; for we should be inclined to say that infinity can't be expressed in them, that is, that we can only conceive of it in our thoughts & hence that it is in these thoughts that the finite and infinite game must be distinguished. (It is queer though that these thoughts should be capable of being expressed in signs.) Let us consider two games. They are both played with cards carrying numbers, and the highest number takes the trick.
). One game is played with a fixed number of such cards, say 32. In the other game we are under certain circumstances allowed to increase the number of cards to as many as we like, by cutting pieces of paper and writing numbers on them. We will call the first of these games bounded, the second unbounded. Suppose a hand of the second game was played & the number of cards actually used was 32. What is the difference in this case between playing a hand a) of the unbounded game & playing a hand b) of the bounded game?
The difference will not be that between a hand of a bounded game with 32 cards and a hand of a bounded game with a greater number of cards. The number of cards used was, we said, the same. But there will be differences of another kind, e.g., the bounded game is played with a normal pack of cards, the unbounded game with a large supply of blank cards & pencils.
Template:BBB TS reference The unbounded game is opened with the question, “How high shall we go?” If the players look up the rules of this game in a book of rules, they will find the phrase “& so on” or “& so on ad inf.” at the end of certain series of rules. So the difference between the two hands a) & b) lies in the tools we use, though admittedly not in the cards they are played with. But this difference seems trivial and not the essential difference between the games. We feel that there must be a big & essential difference somewhere. But if you look closely at what happens when the hands are played, you find that you can only detect a number of differences in details, each of which would seem inessential. The acts, e.g., of dealing & playing the cards may in both cases be identical. In the course of playing the hand a), the players may have considered making up more cards, & again discarded the idea. But what was it like to consider this? It could be some such process as saying to themselves or aloud, “I wonder whether I should make up another card”. Again, no such consideration may have entered the minds of the players. It is possible that the whole difference in the events of a hand of the bounded, and a hand of the unbounded game lay in what was said before the game started, e.g., “Let's play the bounded game”.
“But isn't it correct to say that hands of the two different games belong to two different systems?” Certainly. Only the facts which we are referring to by saying that they belong to different systems are much more complex than we might expect them to be.
Let us now compare language-games of which we should say Template:BBB TS reference that they are played with a limited set of numerals with language-games of which we should say that they are played with the endless series of numerals.
). Like 2) A orders B to bring him a number of building stones. The numerals are the signs “1”, “2”, etc. … “9”, each written on a card. A has a set of these cards and gives B the order by shewing him one of the set & calling out one of the words, “slab”, “column”, etc.
). Like 23), only there is no set of indexed cards. The series of numerals 1 … 9 is learned by heart. The numerals are called out in the orders, & the child learns them by word of mouth.
). An abacus is used. A sets the abacus, gives it to B, B goes with it to where the slabs lie, etc.
). B is to count the slabs in a heap. He does it with an abacus, the abacus has twenty beads. There are never more than 20 plates in a heap. B sets the abacus for the heap in question & shews A the abacus thus set.
). Like 26). The abacus has 20 small beads & one large one. If the heap contains more than 20 plates, the large bead is moved. (So the large bead in some way corresponds to the word “many”).
). Like 26). If the heap contains n plates, n being more than 20 but less than 40, B moves n-20 beads, shews A the abacus thus set, & claps his hand once.
). A & B use the numerals of the decimal system (written or spoken) up to 20. The child learning this language learns these Template:BBB TS reference numerals by heart, etc., as in 2).
). A certain tribe has a language of the kind 2). The numerals used are those of our decimal system. No one numeral used can be observed to play the predominant role of the last numeral in some of the above games (27), 28)). (One is tempted to continue this sentence by saying, “although there is of course a highest numeral actually used”). The children of the tribe learn the numerals in this way: They are taught the signs from 1 to 20 as in 2) and to count rows of beads of no more than 20 on being ordered, “Count these”. When in counting the pupil arrives at the numeral 20, one makes a gesture suggestive of “Go on”, upon which the child says (in most cases at any rate) “21”. Analogously, the children are made to count to 22 & to higher numbers, no particular number playing in these exercises the predominant role of a last one. The last stage of the training is that the child is ordered to count a group of objects, well above 20, without the suggestive gesture being used to help the child over the numeral 20. If a child does not respond to the suggestive gesture, it is separated from the others and treated as a lunatic.
). Another tribe. Its language is like that in 30). The highest numeral observed in use is 159. In the life of this tribe the numeral 159 plays a peculiar role. Supposing I said, “They treat this number as their highest”, – – but what does this mean? Could we answer: “They just say that it is the highest”? ‒ ‒ They say certain words, but how do we know what they mean by them? A criterion for what they mean would be the occasions Template:BBB TS reference on which the word we are inclined to translate into our word “highest” is used, the role, we might say, which we observe this word to play in the life of the tribe. In fact we could easily imagine the numeral 159 to be used on such occasions, in connection with such gestures and forms of behaviour as would make us say that this numeral plays the role of an unsurmountable limit, even if the tribe had no word corresponding to our “highest”, and the criteria for numeral 159 being the highest numeral did not consist of anything that was said about the numeral.
). A tribe has two systems of counting. People learned to count with the alphabet from A to Z and also with the decimal system as in 30). If a man is to count objects with the first system, he is ordered to count “in the closed way”, in the second case, “in the open way”; & the tribe uses the words “closed” & “open” also for a closed and open door.
(Remarks: 23) is limited in an obvious way by the set of cards. 24): Note analogy and lack of analogy between the limited supply of cards in 23) & of words in our memory in 24). Observe that the limitation in 26) on the one hand lies in the tool (the abacus of 20 beads) & its usage in our game, on the other hand (in a totally different way) in the fact that in the actual practice of playing the game no more than 20 objects are ever to be counted. In 27) that latter kind of limitation was absent, but the large bead rather stressed the limitation of our means. Is 28) a limited or an unlimited game? The practice we have described gives the limit 40. We are inclined to say this game “has it in it” to be continued indefinitely, but remember Template:BBB TS reference that we could also have construed the preceding games as beginnings of a system. In 29) the systematic aspect of the numerals used is even more conspicuous than in 28). One might say that there was no limitation imposed by the tools of this game, if it were not for the remark that the numerals up to 20 are learnt by heart. This suggests the idea that the child is not taught to “understand” the system which we see in the decimal notation. Of the tribe in 30) we should certainly say that they are trained to construct numerals indefinitely, that the arithmetic of their language is not a finite one, that their series of numbers has no end. (It is just in such a case when numerals are constructed “indefinitely” that we say that people have the infinite series of numbers.) 31) might shew you what a vast variety of cases can be imagined in which we should be inclined to say that the arithmetic of the tribe deals with a finite series of numbers, even in spite of the fact that the way in which the children are trained in the use of numerals suggests no upper limit. In 32) the terms “closed” & “open” (which could by a slight variation of the example be replaced by “limited” and “unlimited”) are introduced into the language of the tribe itself. Introduced in that simple and clearly circumscribed game, there is of course nothing mysterious about the use of the word “open”. But this word corresponds to our “infinite”, & the games we play with the latter differ from 31) only by being vastly more complicated. In other words, our use of the word “infinite” is just as straight forward as that of “open” in 31 || 32?), and our idea that its meaning is Template:BBB TS reference “transcendent” rests on a misunderstanding.)
We might say roughly that the unlimited cases are characterized by this: that they are not played with a definite supply of numerals, but instead with a system for constructing numerals (indefinitely). When we say that someone has been supplied with a system for constructing numerals, we generally think of either of three things: a) of giving him a training similar to that described in 30), which, experience teaches us, will make him pass tests of the kind mentioned there; b) of creating a disposition in the same man's mind, or brain, to react in that way; c) of supplying him with a general rule for the construction of numerals.
What do we call a rule? Consider this example:
). B moves about according to rules which A gives him. B is supplied with the following table:
a
b
c
d
→
←
↑
↓
A gives an order made up of the letters in the table, say: “a a c a d d d”. B looks up the arrow corresponding to each letter of the order and moves accordingly; in our example thus:
→
→
↑
→
↓
↓
↓
The table 33) we should call a rule (or else “the expression of a rule”. Why I give these synonymous expressions will appear later.) We shan't be inclined to call the sentence “a a c a d d d” itself a rule. It is of course the description of the way B has to take. On the other hand, such a description would under certain circumstances be called a rule, e.g., in the following case:
). B is to draw various ornamental linear designs. Each design is a repetition of one element which A gives him. Thus if A gives the order “c a d a”, B draws a line thus:
In this case I think we should say that “c a d a” is the rule for drawing the design. Roughly speaking, it characterizes what we call a rule to be applied repeatedly, in an indefinite number of instances. Cf., e.g., the following case with 34):
). A game played with pieces of various shapes on a chess board. The way each piece is allowed to move is laid down by a rule. Thus the rule for a particular piece is “ac”, for another piece “acaa”, & so on. The first piece then can make a move like this:
→
↑
, the second, like this:
→
↑
→
→
. Both a formula like “ac” or a diagram like that corresponding to such a formula might here be called a rule.
). Suppose that after playing the game 33) several times as described above, it was played with this variation: that B no longer looked at the table, but reading A's order the letters call up the images of the arrows (by association), & B acts according to these imagined arrows.
). After playing it like this for several times, B moves about according to the written order as he would have done had he looked up or imagined the arrows, but actually without any such picture intervening. Imagine even this variation:
). B in being trained to follow a written order, is shewn the table of 33) once, upon which he obeys A's orders without further intervention of the table in the same way in which B in
Template:BBB TS reference 33) does with the help of the table on each occasion.
In each of these cases, we might say that the table 33) is a rule of the game. But in each one this rule plays a different role. In 33) the table is an instrument used in what we should call the practice of the game. It is replaced in 36) by the working of association. In 37) even this shadow of the table has dropped out of the practice of the game, and in 38) the table is admittedly an instrument for the training of B only.
But imagine this further case:
). A certain system of communication is used by a tribe. I will describe it by saying that it is similar to our game 38) except that no table is used in the training. The training might have consisted in several times leading the pupil by the hand along the path one wanted him to go. But we could also imagine a case:
). where even this training is not necessary, where, as we should say, the look of the letters abcd naturally produced an urge to move in the way described. This cause at first sight looks puzzling. We seem to be assuming a most unusual working of the mind. Or we may ask || perhaps we ask, “How on earth is he to know which way to move if the letter a is shewn him”? But isn't B's reaction in this case the very reaction described in 37) & 38), & in fact our usual reaction when for instance we hear and obey an order? For, the fact that the training in 38) & 39) preceded the carrying out of the order does not change the process of carrying out. In other words the “curious mental mechanism” assumed in 40) is no other than that which we assumed to be
Template:BBB TS reference created by the training in 37) and 38). “But could such a mechanism be born with you?” But did you find any difficulty in assuming that that mechanism was born with B, which enabled him to respond to the training in the way he did? And remember that the rule or explanation given in table 33) of the signs abcd was not essentially the last one, and that we might have given a table for the use of such tables, and so on. (Cf. 21)).
How does one explain to a man how he should carry out the order, “Go this way!” (pointing with an arrow the way he should go)? Couldn't this mean going the direction which we should call the opposite of that of the arrow? Isn't every explanation of how he should follow the arrow in the position of another arrow? What would you say to this explanation: A man says, “If I point this way (pointing with his right hand) I mean you to go like this” (pointing with his left hand the same way)? This just shews you the extremes between which the uses of signs vary.
Let us return to 39). Someone visits the tribe and observes the use of the signs in their language. He describes the language by saying that its sentences consist of the letters abcd used according to the table: (of 33)). We see that the expression, “A game is played according to the rule so-and-so” is used not only in the variety of cases exemplified by 36), 37), & 38), but even in cases where the rule is neither an instrument of the training nor of the practice of the game, but stands in the relation to it in which our table stands to the practice of our game 39). One might in this case call the table a natural
Template:BBB TS reference law describing the behaviour of the people of this tribe. Or we might say that the table is a record belonging to the natural history of the tribe.
Note that in the game 33) I distinguished sharply between the order to be carried out and the rule employed. In 34) on the other hand, we called the sentence “c a d a” a rule, & it was the order. Imagine also this variation:
). The game is similar to 33), but the pupil is not just trained to use a single table; but the training aims at making the pupil use any table correlating letters with arrows. Now by this I mean no more than that the training is of a peculiar kind, roughly speaking one analogous to that described in 30). I will refer to a training more or less similar to that in 30) as a “general training”. General trainings form a family whose members differ greatly from one another. The kind of thing I'm thinking of now mainly consists: a) of a training in a limited range of actions, b) of giving the pupil a lead to extend this range, & c) of random exercises and tests. After the general training the order is now to consist in giving him a sign of this kind:
rr
r
s
t
tst
↗
↖
↓He carries out the order by moving thus: . Here I suppose we should say the table, the rule, is part of the order.
Note, we are not saying “what a rule is” but just giving different applications of the word “rule”; & we certainly do this by giving applications of the words “expression of a rule”.
Note also that in 41) there is no clear case against calling
Template:BBB TS reference the whole symbol given the sentence, though we might distinguish in it between the sentence and the table. What in this case more particularly tempts us to this distinction is the linear writing of the part outside the table. Though from certain points of view we should call the linear character of the sentence merely external and inessential, this character and similar ones play a great role in what as logicians we are inclined to say about sentences and propositions. And therefore if we conceive of the symbol in 41) as a unit, this may make us realise what a sentence can look like.
Let us now consider these two games:
). A gives orders to B: they are written signs consisting of dots and dashes and B executes them by doing a figure in dancing with a particular step. Thus the order “-.” is to be carried out by taking a step and a hop alternately; the order “..---” by alternately taking two hops and three steps, etc. The training in this game is “general” in the sense explained in 41); and I should like to say, “the orders given don't move in a limited range. They comprise combinations of any number of dots and dashes”. ‒ ‒ But what does it mean to say that the orders don't move in a limited range? Isn't this nonsense? Whatever orders are given in the practice of the game constitute the limited range. ‒ ‒ Well, what I meant to say by “the orders don't move in a limited range” was that neither in the teaching of the game nor in the practice of it a limitation of the range plays a “predominant” role (see 30)) or, as we might say, the range of the game (it is superfluous to say
Template:BBB TS reference limited) is just the extent of its actual (“accidental”) practice. (Our game is in this way like 30)) Cf. with this game the following:
). The orders and their execution as in 42); but only these three signs are used: “-.”, “-..”, “.--”. We say that in 42) B in executing the order is guided by the sign given to him. But if we ask ourselves whether the three signs in 43) guide B in executing the orders, it seems that we can say both yes and no according to the way we look at the execution of the orders.
If we try to decide whether B in 43) is guided by the signs or not, we are inclined to give such answers as the following: a) B is guided if he doesn't just look at an order, say “.--” as a whole and then act, but if he reads it “word by word” (the words used in our language being “.” “-”) and acts according to the words he has read.
We could make these cases clearer if we imagine that the “reading word by word” consisted in pointing to each word of the sentence in turn with one's finger as opposed to pointing at the whole sentence at once, say by pointing to the beginning of the sentence. And the “acting according to the words” we shall for the sake of simplicity imagine to consist in acting (stepping or hopping) after each word of the sentence in turn. ‒ ‒ b) B is guided if he goes through a conscious process which makes a connection between the pointing to a word and the act of hopping and stepping. Such a connection could be imagined in many different ways. E.g., B has a table in which a dash
Template:BBB TS reference is correlated to the picture of a man making a step and a dot to a picture of a man hopping. Then the conscious acts connecting reading the order and carrying it out might consist in consulting the table, or in consulting a memory image of it “with one's mind's eye”. c) B is guided if he does not just react to looking at each word of the order, but experiences the peculiar strain of “trying to remember what the sign means”, & further, the relaxing of this strain when the meaning, the right action, comes before his mind.
All these explanations seem in a peculiar way unsatisfactory, and it is the limitation of our game which makes them unsatisfactory. This is expressed by the explanation that B is guided by the particular combination of words in one of our three sentences if he could also have carried out orders consisting in other combinations of dots and dashes. And if we say this, it seems to us that the “ability” to carry out other orders is a particular state of the person carrying out the orders of 42). And at the same time we can't in this case find anything which we should call such a state.
Let us see what role the words “can” or “to be able to” play in our language. Consider these examples:
). Imagine that for some purpose or other people use a kind of instrument or tool; this consists of a board with a slot in it guiding the movement of a peg. The man using the tool slides the peg along the slot. There are such boards with straight slots, circular slots, elliptic slots, etc. The language of the people using this instrument has expressions for
Template:BBB TS reference describing the activity of moving the peg in the slot. They talk of moving it in a circle, in a straight line, etc. They also have a means of describing the board used. They do it in this form: “This is a board in which the peg can be moved in a circle”. One could in this case call the word “can” an operator by means of which the form of expression describing an action is transformed into a description of the instrument.
). Imagine a people in whose language there is no such form of sentence as “the book is in the drawer” or “water is in the glass”, but wherever we should use these forms they say, “The book can be taken out of the drawer”, “The water can be taken out of the glass”.
). An activity of the men of a certain tribe is to test sticks as to their hardness. They do it by trying to bend the sticks with their hands. In their language they have expressions of the form, “This stick can be bent easily” or “This stick can be bent with difficulty”. They use these expressions as we use “This stick is soft” or “This stick is hard”. I mean to say that they don't use the expression, “This stick can be bent easily” as we should use the sentence “I am bending the stick with ease”. Rather they use their expression in a way which would make us say that they are describing a state of the stick. I.e., they use such sentences as, “This hut is built of sticks that can be bent easily”. (Think of the way in which we form adjectives out of verbs by means of the ending “-able”, e.g., “deformable”.)
Now we might say that in the last three cases the sentences
Template:BBB TS reference of the form “so-and-so can happen” described the state of objects, but there are great differences between these examples. In 44) we saw the state described before our eyes. We saw that the board had a circular or a straight slot, etc. In 45), in some instances at least this was the case, we could see the objects in the box, the water in the glass, etc. In such cases we use the expression “state of an object” in such a way that there corresponds to it what one might call a stationary sense experience.
When on the other hand, we talk of the state of a stick in 46), observe that to this “state” there does not correspond a particular sense experience which lasts while the state lasts. Instead of that, the defining criterion for something being in this state consists in certain tests.
We may say that a car travels 20 miles an hour even if it only travels for half an hour. We can explain our form of expression by saying that the car travels with a speed which enables it to make 20 miles an hour. And here also we are inclined to talk of the velocity of the car as of a state of its motion. I think we should not use this expression if we had no other “experiences of motion” than those of a body being in a particular place at a certain time and in another place at another time; if, e.g., our experiences of motion were of the kind which we have when we see the hour hand of the clock has moved from one point of the dial to the other.
). A tribe has in its language commands for the execution of certain actions of men in warfare, something like “Shoot!”,
Template:BBB TS reference “Run!”, “Crawl!”, etc. They also have a way of describing a man's build. Such a description has the form “He can run fast”, “He can throw the spear far”. What justifies me in saying that these sentences are descriptions of the man's build is the use which they make of sentences of this form. Thus if they see a man with bulging leg muscles but who as we should say has not the use of his legs for some reason or other, they say he is a man who can run fast. The drawn image of a man which shews large biceps they describe as representing a man “who can throw a spear far”.
). The men of a tribe are subjected to a kind of medical examination before going into war. The examiner puts the men through a set of standardised tests. He lets them lift certain weights, swing their arms, skip, etc. The examiner then gives his verdict in the form “So-and-so can throw a spear” or “can throw a boomerang” or “is fit to pursue the enemy”, etc. There are no special expressions in the language of this tribe for the activities performed in the tests; but these are referred to only as the tests for certain activities in warfare.
It is an important remark concerning this example and others which we give that one may object to the description which we give of the language of a tribe, that in the specimens we give of their language we let them speak English, thereby already presupposing the whole background of the English language, that is, our usual meanings of the words. Thus if I say that in a certain language there is no special verb for “skipping”, but that this language uses instead the form “making Template:BBB TS reference the test for throwing the boomerang”, one may ask how I have characterized the use of the expressions, “make a test for” & “throwing the boomerang”, to be justified in substituting these English expressions for whatever their actual words may be. To this we must answer that we have only given a very sketchy description of the practices of our fictitious languages, in some cases only hints, but that one can easily make these descriptions more complete. Thus in 48) I could have said that the examiner uses orders for making the men go through the tests. These orders all begin with one particular expression which I could translate into the English words, “Go through the test”. And this expression is followed by one which in actual warfare is used for certain actions. Thus there is a command upon which men throw their boomerangs and which therefore I should translate into, “Throw the boomerangs”. Further, if a man gives an account of the battle to his chief, he again uses the expression I have translated into “Throw a boomerang”, this time in a description. Now what characterizes an order as such or a description as such or a question as such, etc., is – – as we have said – – the role which the utterance of these signs plays in the whole practice of the language. That is to say, whether a word of the language of our tribe is rightly translated into a word of the English language depends upon the role this word plays in the whole life of the tribe; the occasions on which it is used, the expressions of emotions by which it is generally accompanied, the ideas which it generally awakens or which prompt its saying, etc. etc. As an exercise ask yourself: in which
Template:BBB TS reference cases would you say that a certain word uttered by the people of the tribe was a greeting? In which cases should we say it corresponded to our “Goodbye”, in which to our “Hello”? In which cases would you say that a word of a foreign language corresponded to our “perhaps”? – – to our expressions of doubt, trust, certainty? You will find that the justifications for calling something an expression of doubt, conviction, etc. largely, though of course not wholly, consist in descriptions of gestures, the play of facial expressions, and even the tone of voice. Remember at this point that the personal experiences of an emotion must in part be strictly localized experiences; for if I frown in anger I feel the muscular tension of the frown in my forehead, & if I weep, the sensations around my eyes are obviously part, and an important part, of what I feel. This is, I think, what William James meant when he said that a man doesn't cry because he is sad but that he is sad because he cries. The reason why this point is often not understood is that we think of the utterance of an emotion as though it were some artificial device to let others know that we have it. Now there is no sharp line between such “artificial devices” and what one might call the natural expressions of emotion. Cf. in this respect: a) weeping, b) raising one's voice when one is angry, c) writing an angry letter, d) ringing the bell for a servant you wish to scold.
). Imagine a tribe in whose language there is an expression corresponding to our “He has done so-and-so” and another expression corresponding to our “He can do so-and-so”, this latter
Template:BBB TS reference expression, however, being only used where its use is justified by the same fact which would also justify the former expression. Now what can make me say this? They have a form of communication which we should call narration of past events because of the circumstances under which it is employed. There are also circumstances under which we should ask and answer such questions as “Can so-and-so do this?”. Such circumstances can be described, e.g., by saying that a chief picks men suitable for a certain action, say crossing a river, climbing a mountain, etc. As the defining criteria of “the chief picking men suitable for this action”, I will not take what he says but only the other features of the situation. The chief under these circumstances asks a question which, as far as its practical consequences go, would have to be translated by our “Can so-and-so swim across this river?” This question, however, is only answered affirmatively by those who actually have swum across this river. This answer is not given in the same words in which under the circumstances characterizing narration he would say that he has swum across this river, but it is given in the terms of the question asked by the chief. On the other hand, this answer is not given in cases in which we should certainly give the answer, “I can swim across this river”, if, e.g., I had performed more difficult feats of swimming though not just that of swimming across this particular river.
By the way, have the two phrases, “He has done so-&-so” and “He can do so-&-so” the same meaning in this language or have they different meanings? If you think about it, something
Template:BBB TS reference will tempt you to say the one, something to say the other. This only shows that the question has here no clearly defined meaning. All I can say is: If the fact that they only say, “He can … ” if he has done … is your criterion for the same meaning, then the two expressions have the same meaning. If the circumstances under which an expression is used make its meaning, the meanings are different. The use which is made of the word “can” – – the expression of possibility in 49) – – can throw a light upon the idea that what can happen must have happened before (Nietzsche). It will also be interesting to look, in the light of our examples, on the statement that what happens can happen.
Before we go on with our consideration of the use of “the expression of possibility”, let us get clearer about that department of our language in which things are said about past & future, that is, about the use of sentences containing such expressions as “yesterday”, “a year ago”, “in five minutes”, “before I did this”, etc. Consider this example:
). Imagine how a child might be trained in the practice of “narration of past events”. He was first trained in asking for certain things (as it were, in giving orders. See 1).) Part of this training was the exercise of “naming the things”. He has thus learnt to name (& ask for) a dozen of his toys. Say now that he has played with three of them (e.g., a ball, a stick, and a rattle), then they are taken away from him, and now the grown-up says such a phrase as, “He's had a ball, a stick, and a rattle”. On a similar occasion he stops short in the enumeration
Template:BBB TS reference and induces the child to complete it. On another occasion, perhaps, he only says, “He's had … ” and leaves the child to give the whole enumeration. Now the way of “inducing the child to go on” can be this: He stops short in his enumeration with a facial expression and a raised tone of voice which we should call one of expectancy. All then depends on whether the child will react to this “inducement” or not. Now there is a queer misunderstanding we are most liable to fall into, which consists in regarding the “outward means” the teacher uses to induce the child to go on as what we might call an indirect means of making himself understood to the child. We treat || regard the case as though the child already possessed a language in which it thought and that the teacher's job is to induce it to guess his meaning in the realm of meanings before the child's mind, as though the child could in his own private language ask himself such a question as, “Does he want me to continue, or repeat what he said, or something else?” (Cf. with 30)).
). Another example of a primitive kind of narration of past events: we live in a landscape with characteristic natural landmarks against the horizon. It is therefore easy to remember the place at which the sun rises at a particular season, or the place above which it stands when at its highest point, or the place at which it sets. We have some characteristic pictures of the sun in different positions in our landscape. Let us call this series of pictures the sun series. We have also some characteristic pictures of the activities of a child, lying in bed, getting up, dressing, lunching, etc. This set
Template:BBB TS reference I'll call the life pictures. I imagine that the child can frequently see the position of the sun while about the day's activities. We draw the child's attention to the sun's standing in a certain place while the child is occupied in a particular way. We then let it look both at a picture representing its occupation and at a picture showing the sun in its position at that time. We can thus roughly tell the story of the child's day by laying out a row of the life pictures, and above it what I called the sun series, the two rows in the proper correlation. We shall then proceed to let the child supplement such a picture story, which we leave incomplete. And I wish to say at this point that this form of training (see 50) and 30)) is one of the big characteristic features in the use of language, or in thinking.
). A variation of 51). There is a big clock in the nursery, for simplicity's sake imagine it with an hour hand only. The story of the child's day is narrated as above, but there is no sun series; instead we write one of the digits || numbers of the dial against each life picture.
). Note that there would have been a similar game in which also, as we might say, time was involved, that of just laying out a series of life pictures. We might play this game with the help of words which would correspond to our “before” and “after”. In this sense we may say that 53) involves the ideas of before and after, but not the idea of a measurement of time. I needn't say that an easy step would lead us from the narrations in 51), 52), & 53) to narrations in words. Possibly someone
Template:BBB TS reference considering such forms of narration might think that in them the real idea of time isn't yet involved at all, but only some crude substitute for it, the position of a clock hand and such like. Now if a man claimed that there is an idea of “five o'clock” which does not bring in a clock, that the clock is only the coarse instrument indicating when it is five o'clock or that there is an idea of an hour which does not bring in an instrument for measuring the time, I will not contradict him, but I will ask him to explain to me what his use of the term “an hour” or “five o'clock” is. And if it is not that involving a clock, it is a different one; and then I will ask him why he uses the term “five o'clock”, “an hour”, “a long time”, “a short time”, etc., in one case in connection with a clock, in the other independent of one; it will be because of certain analogies holding between the two uses, but we have now two uses of these terms, and no reason to say that one of them is less real and pure than the other. This might get clearer by considering the following example:
). If we give a person the order, “Say a number, any one which comes into your mind”, he can generally comply with it at once. Suppose it were found that the numbers thus said on request increased – – with every normal person – – as the day went on; a man starts out with some small number every morning and reaches the highest number before falling asleep at night. Consider what could tempt one to call the reactions described “a means of measuring time” or even to say that they are the real milestones in the passage of time, the sun clocks, etc.
Template:BBB TS reference being only indirect markers. || indicators. (Examine the statement that the human heart is the real clock behind all the other clocks).
Let us now consider further language-games into which temporal expressions enter.
). This arises out of 1). If an order like “Slab!”, “Column!”, etc. is called out, B is trained to carry it out immediately. We now introduce a clock into this game, an order is given, and we train the child not to carry it out until the hand of our clock reaches a point indicated before with the finger. (This might, e.g., be done in this way: You first trained the child to carry out the order immediately. You then give the order, but hold the child back, releasing it only when the hand of the clock has reached the point of the dial to which we point with our fingers.)
We could at this stage introduce such a word as “now”. We have two kinds of orders in this game, the orders used in 1), and orders consisting of these together with a gesture indicating a point of the clock dial. In order to make the distinction between these two kinds more explicit, we may affix a particular sign to the orders of the first kind and e.g., say: “slab, now!”.
It would be easy now to describe language-games in such expressions as “in five minutes”, “half an hour ago”.
). Let us now have the case of a description of the future, a forecast. One might, e.g., awaken the tension of expectation in a child by keeping his attention for a considerable time on some traffic lights changing their colour periodically. We also have a red, a green, and a yellow disc before us and alternately
Template:BBB TS reference point to one of these discs by way of forecasting the colour which will appear next. It is easy to imagine further developements of this game.
Looking at these language-games, we don't come across the ideas of the past, the future, and the present in their problematic and almost mysterious aspect. What this aspect is and how it comes about that it appears can be most characteristically exemplified if we look at the question, “Where does the present go when it becomes past, and where is the past?” – – under what circumstances has this question an allurement for us? For under certain circumstances it hasn't, and we should wave it away as nonsense.
It is clear that this question most easily arises if we are preoccupied with cases in which there are things flowing by us, – – as logs of wood float down a river. In such a case we can say the logs which have passed us are all down towards the left and the logs which will pass us are all up towards the right. We then use this situation as a simile for all happening in time and even embody the simile in our language, as when we say that “the present event passes by” (a log passes by), “the future event is to come” (a log is to come). We talk about the flow of events; but also about the flow of time – – the river on which the logs travel.
Here is one of the most fertile sources of philosophic puzzlement: We talk of the future event of something coming into my room, and also of the future coming of this event.
We say, “Something will happen”, and also, “Something
Template:BBB TS reference comes towards me”; we refer to the log as to “something”, but also to the log's coming towards me.
Thus it can come about that we aren't able to rid ourselves of the implications of our symbolism, which seems to admit of a question like, “where does the flame of a candle go to when it's blown out?”, “Where does the light go to?”, “Where does the past go to?”. We have become obsessed with our symbolism. We may say that we are led into puzzlement by an analogy which irresistibly drags us on. ‒ ‒ And this also happens when the meaning of the word “now” appears to us in a mysterious light. In our example 55) it appears that the function of “now” is in no way comparable to the function of an expression like “five o'clock”, “midday”, “the time when the sun sets”, etc. This latter group of expressions I might call “specifications || “determinations of times”. But our ordinary language uses the word “now” and determinations of time in similar contexts. Thus we say “The sun sets now”. || “The sun sets at six o' clock”. We are inclined to say that both “now” and “six o'clock” “refer to points of time”. This use of words produces a puzzlement which one might express in the question, “What is the ‘now’? – – for it is a moment of time and yet it can't be said to be either the ‘moment at which I speak’ or the ‘moment at which the clock strikes’ etc., etc.”‒ ‒ Our answer is: The function of the word “now” is entirely different from that of a specification of time. ‒ ‒ This can easily be seen if we look at the role this word really plays in our usage of language, but it is obscured when instead of looking at the whole language-game, we only look at the contexts, the phrases Template:BBB TS reference of language in which the word is used. (The word “today” is not a date, but it isn't anything like it either. It doesn't differ from a date as a hammer differs from a mallet, but as a hammer differs from a nail; and surely we may say there is both a connection between a hammer and a mallet and between a hammer and a nail.)
One has been tempted to say that “now” is the name of an instant of time, and this, of course, would be like saying that “here” is the name of a place, “this” the name of a thing, and “I” the name of a man. (One could of course also have said “a year ago” was the name of a time, “over there” the name of a place, and “you” the name of a person.) But nothing is more unlike than the use of the word “this” and the use of a proper name, – – I mean the games played with these words, not the phrases in which they are used. For we do say, “This is short” and “Jack is short”; but remember that “This is short” without the pointing gesture and without the thing we are pointing to would be meaningless. ‒ ‒ What can be compared with a name is not the word “this” but, if you like, the symbol consisting of this word, the gesture, and the sample. We might say: Nothing is more characteristic of a proper name A than that we can use it in such a phrase as, “This is A”; & it makes no sense to say, “This is this” or “Now is now” or “Here is here”.
The idea of a proposition saying something about what will happen in the future is even more liable to puzzle us than the idea of a proposition about the past. For comparing future events with past events, one may almost be inclined to say that
Template:BBB TS reference though the past events do not really exist in the full light of day, they exist in an underworld into which they have passed out of the real life; whereas the future events do not even have this shadowy existence. We could, of course, imagine a realm of the unborn, future events, whence they come into reality and pass into the realm of the past; and, thinking || if we think in terms of this metaphor, we may be surprised that the future should appear less existent than the past. Remember, however, that the grammar of our temporal expressions is not symmetrical with respect to an origin corresponding with the present moment. Thus the grammar of the expressions relating to memory does not reappear “with opposite sign” in the grammar of the future tense. || Thus there is nothing in the grammar of the future tense corresponding to the grammar of the word “memory”. This part of the grammar of the past tense does not recur “with its sign changed” on the future side. This is the reason why it has been said that propositions concerning future events are not really propositions. And to say this, is all right as long as it isn't meant to be more than a decision about the use of the term “proposition”; a decision which, though not agreeing with the common usage of the word “proposition”, may come natural to human beings under certain circumstances. If a philosopher says that propositions about the future are not real propositions, it is because he has been struck by the asymmetry in the grammar of temporal expressions. The danger is, however, that he imagines he has made a kind of scientific statement about “the nature of the future”.
Template:BBB TS reference ). A game is played in this way: A man throws a die, and before throwing he draws on a piece of paper some one of the six faces of the die. If, after having thrown, the face of the die turning up is the one he has drawn, he feels (expresses) satisfaction. If a different face turns up, he is dissatisfied. Or, let there be two partners and every time one guesses correctly what he will throw his partner pays him a penny, and if incorrectly, he pays his partner. Drawing the face of the die will under the circumstances of this game be called “making a guess” or a “conjecture”.
). In a certain tribe contests are held in running, putting the weight, etc. and the spectators stake money || possessions on the competitors. The pictures of all the competitors are placed in a row, and what I called the spectators' staking property on one of the competitors consists in laying this property (pieces of gold) under one of the pictures. If a man has placed his gold under the picture of the winner in the competition he gets back his stake doubled. Otherwise he loses his stake. Such a custom we should undoubtedly call betting, even if we observed it in a society whose language held no scheme for stating “degrees of probability”, “chances” and the like. I assume that the behaviour of the spectators expresses great keenness and excitement before and after the result || outcome of the bet is known. I further imagine that on examining the placing of the bets I can understand “why” they were thus placed. I mean: In a competition between two wrestlers, mostly the bigger man is the favorite; or if the smaller, I find that he has shown greater
Template:BBB TS reference strength on previous occasions, or that the bigger had recently been ill, or had neglected his training, etc. Now this may be so although the language of the tribe does not express reasons for the placing of the bets. That is to say, nothing in their language corresponds to our saying, e.g., “I bet on this man because he has kept fit, whereas the other has neglected his training”, and such like. I might describe this state of affairs by saying that my observation has taught me certain causes for their placing their bets as they do, but that the bettors had || used no reasons for acting as they did.
The tribe may, on the other hand, have a language which comprises “giving reasons”. Now this game of giving the reason why one acts in a particular way does not involve finding the causes of one's actions (by frequent observations of the conditions under which they arise). Let us imagine this:
). If a man of our tribe has lost his bet and upon this is chaffed or scolded, he points out, possibly exaggerating, certain features of the man on whom he has laid his bet. One can imagine a discussion of pros and cons going on in this way: two people pointing out alternately certain features of the two competitors whose chances, as we should say, they are discussing; A pointing with a gesture to the great height of the one, B in answer to this shrugging his shoulders and pointing to the size of the other's biceps, and so on. I could easily add more details which would make us say that A and B are giving reasons for laying a bet on one person rather than on the other.
Now one might say || suggest that giving reasons in this way for
Template:BBB TS reference laying their bets certainly presupposes that they have observed causal connections between the result of a fight, say, and certain features of the bodies of the fighters, or of their training. But this is an assumption which, whether reasonable or not, I certainly have not made in the description of our case. (Nor have I made the assumption that the bettors give reasons for their reasons.) We should in a case like that just described not be surprised if the language of the tribe contained what we should call expressions of degrees of belief, conviction, certainty. These expressions we could imagine to consist in the use of a particular word spoken with different intonations, or a series of words. (I am not thinking however of the use of a scale of probabilities.) ‒ ‒ It is also easy to imagine that the people of our tribe accompany their betting by verbal expressions which we translate into, “I believe that so-and-so can beat so-and-so in wrestling”, etc.
). Imagine in a similar way conjectures being made as to whether a certain load of gunpowder will be sufficient to blast a certain rock, and the conjecture to be expressed in a phrase of the form, “This quantity of gunpowder can blast this rock”.
). Compare with 60) the case in which the expression, “I shall be able to lift this weight”, is used as an abbreviation for the conjecture, “My hand holding this weight will rise if I go through the process (experience) of ‘making an effort to lift it’”. In the last two cases the word “can” characterized what we should call the expression of a conjecture. (Of course
Template:BBB TS reference I don't mean that we call the sentence a conjecture because it contains the word “can”; but in calling a sentence a conjecture we referred to the role which the sentence played in the language-game; and we translate a word our tribe uses by “can” if “can” is the word we should use under the circumstances described). Now it is clear that the use of “can” in 59), 60), 61) is closely related to the use of “can” in 46) to 49); differing, however in this, that in 46) to 49) the sentences saying that something could || can happen were not expressions of conjecture. Now one might object to this by saying: Surely we are only willing to use the word “can” in such cases as 46) to 49) because it is reasonable to conjecture in these cases what a man will do in the future from the tests he has passed or from the state he is in.
Now it is true that I have deliberately made up the cases 46) to 49) so as to make a conjecture of this kind seem reasonable. But I have also deliberately made them up so as not to contain a conjecture. We can, if we like, make the hypothesis that the tribe would never use such a form of expression as that used in 49), etc. if experience had not shown them that … etc. But this is an assumption which, though possibly correct, is in no way presupposed in the games 46) to 49) as I have actually described them.
). Let the game be this: A writes down a row of numbers. B watches him and tries to find a system in the sequence of these numbers. When he has done so he says: “Now I can go on”. This example is particularly instructive because “being able to
Template:BBB TS reference go on” here seems to be something setting in suddenly in the form of a clearly outlined event. ‒ ‒ Suppose then that A had written down the row 1,5,11,19,29. At that point B shouts, “Now I can go on”. What was it that happened when suddenly he saw how to go on? A great many different things might have happened. Let us assume then that in the present case while A wrote one number after the other B busied himself with trying out several algebraic formulae to see whether they fitted. When A had written “19” B had been led to try the formula an = n2 + n ‒ 1. A's writing 29 confirms his guess.
). Or, no formula came into B's mind. After looking at the growing row of numbers A was || is writing, possibly with a feeling of tension and with hazy ideas floating in his mind, he said to himself the words, “He's squaring and always adding one more”; then he made up the next number of the sequence and found it to agree with the numbers A then wrote down. ‒ ‒
). Or the row A wrote down was 2, 4, 6, 8. B looks at it, and says, “Of course I can go on”, and continues the series of even numbers. Or he says nothing, and just goes on. Perhaps when looking at the row 2, 4, 6, 8 which A had written down, he had some sensation, or sensations, often accompanying such words as, “That's easy!” A sensation of this kind is for instance, the experience of a slight, quick intake of breath, what one might call a slight start.
Now, should we say that the proposition, “B can continue the series”, means that one of the occurrences just described takes place? Isn't it clear that the statement, “B can continue … ”
Template:BBB TS reference is not the same as the statement that the formula an = n2 + n ‒ 1 comes into B's mind? This occurrence might have been all that actually took place. (It is clear, by the way, that it can make no difference to us here whether B has the experience of this formula appearing before his mind's eye, or the experience of writing or speaking the formula, or of picking it out with his eyes from amongst several formulae written down beforehand.) If a parrot had uttered the formula, we should not have said that he could continue the series. ‒ ‒ Therefore, we are inclined to say “to be able to … ” must mean more than just uttering the formula, – – and in fact more than any one of the occurrences we have described. And this, we go on, shows that saying the formula was only a symptom of B's being able to go on, and that it was not the ability of going on itself. Now what is misleading in this is that we seem to intimate that there is one peculiar activity, process, or state called “being able to go on” which somehow is hidden from our eyes but manifests itself in these occurrents which we call symptoms (as an inflammation of the mucous membranes of the nose produces the symptom of sneezing). This is the way talking of symptoms, in this case, misleads us. When we say, “Surely there must be something else behind the mere uttering of the formula, as this alone we should not call ‘being able to … ’”, the word “behind” here is certainly used metaphorically, and “behind” the utterance of the formula may be the circumstances under which it is uttered. It is true, “B can continue … ” is not the same as to say, “B says the formula … ”, but it
Template:BBB TS reference doesn't follow from this that the expression, “B can continue … ” refers to an activity other than that of saying the formula, in the way in which “B says the formula” refers to the well-known activity. The error we are in is analogous to this: Someone is told the word “chair” does not mean this particular chair I am pointing to, upon which he looks round the room for the object which the word “chair” does denote. (The case would be even more a striking illustration if he tried to look inside the chair in order to find the real meaning of the word “chair”.) It is clear that when with reference to the act of writing or speaking the formula etc., we use the sentence, “He can continue the series”, this must be because of some connection between writing down a formula and actually continuing the series. And the connection in experience of these two processes or activities is clear enough. But this connection tempts us to suggest that the sentence, “B can continue … ” means something like, “B does something which, experience has shown us, generally leads to his continuing the series.” But does B, when he says, “Now I can go on” really mean, “Now I am doing something which, as experience has shown us, etc., etc.”? Do you mean that he had this phrase in his mind or that he would have been prepared to give it as an explanation of what he had said?! To say the phrase, “B can continue … ” is correctly used when prompted by such occurrences as described in 62), 63), 64) but that these occurrences justify its use only under certain circumstances (e.g. when experience has shown certain connections) is not to say that the sentence, “B can continue … ”
Template:BBB TS reference is short for the sentence which describes all these circumstances, i.e. the whole situation which is the background of our game.
On the other hand we should under certain circumstances be ready to substitute “B knows the formula”, “B has said the formula” for “B can continue the series”. As when we ask a doctor, “Can the patient walk?”, we shall sometimes be ready to substitute for this, “Is his leg healed?” – – “Can he speak?” under certain circumstances means, “Is his throat all right?”, under others (e.g. if he is a small child) it means, “Has he learned to speak?” ‒ ‒ To the question, “Can the patient walk?”, the doctor's answer may be, “His leg is all right”. ‒ ‒ We use the phrase, “He can walk, as far as the state of his leg is concerned”, especially when we wish to oppose this condition for his walking to some other condition, say the state of his spine. Here we must beware of thinking that there is in the nature of the case something which we might call a || the complete set of conditions, e.g. for his walking; so that the patient, as it were, must walk || can't help walking if all these conditions are fulfilled.
We can say: The expression, “B can continue the series”, is used under different circumstances to make different distinctions. Thus it may distinguish a) between the case when a man knows the formula and the case when he doesn't; or b) between the case when a man knows the formula and hasn't forgotten how to write the numerals of the decimal system, and the case when he knows the formula and has forgotten how to write the numerals; or c) (as perhaps in 64)) between the case when a man is feeling Template:BBB TS reference his normal self and the case when he is still in a condition of shell shock; or d) between the case of a man who has done this kind of exercise before and the case of a man who is new at it. These are only a few of a large family of cases.
The question whether “He can continue … ” means the same as “He knows the formula” can be answered in several different ways: We can say, “They don't mean the same, i.e., they are not in general used as synonyms as, e.g., the phrases, ‘I am well’ and ‘I am in good health’”; or we may say, “Under certain circumstances” ‘He can continue … ’ means he knows the formula”. Imagine the case of a language (somewhat analogous to 49)) in which two forms of expression, two different sentences, are used to say that a person's legs are in working order. The one form of expression is exclusively used under circumstances when preparations are going on for an expedition, a walking tour, or the like; the other is used in cases when there is no question of such preparations. We shall here be doubtful whether to say the two sentences have the same meaning or different meanings. In any case the true state of affairs can only be seen when we look into the detail of the usage of our expressions. ‒ ‒ And it is clear that if in our present case we should decide on saying || to say that the two expressions have different meanings, we shall certainly not be able to say that the difference is that the fact which makes the second sentence true is a different one from the fact which makes the first sentence true.
We are justified in saying that the sentence, “He can Template:BBB TS reference continue … ” has a different meaning from that, “He knows the formula”. But we mustn't imagine that we can find a particular state of affairs “which the first sentence refers to”, as it were on || in a plane above that on || in which the special occurrences (like knowing the formula, imagining certain further terms, etc.) take place.
Let us ask the following question: Suppose that, on one ground or another, B has said, “I can continue the series”, but on being asked to continue it he had shown himself unable to do so, – – should we say that this proved that his statement, that he could continue, was wrong, or should we say that he was able to continue when he said he was? Would B himself say, “I see I was wrong”, or “What I said was true, I could do it then but I can't now”? ‒ ‒ There are cases in which he would correctly say the one and cases in which he would correctly say the other. Suppose a) when he said he could continue he saw the formula before his mind, but when he was asked to continue he found he had forgotten it; – – or, b) when he said he could continue he had said to himself the next five terms of the series, but now finds that they don't come into his mind; – – or c) before, he had continued the series calculating five more places, now he still remembers these five numbers but has forgotten how he had calculated them; – – or d) he says, “Then I felt I could continue, now I can't”; – – or e), “When I said I could lift the weight my arm didn't hurt, now it does”; etc.
On the other hand we say, “I thought I could lift this weight, but I see I can't”, “I thought I could say this piece
Template:BBB TS reference by heart, but I see I was mistaken”.
These illustrations of the || our use of the word “can” should be supplemented by illustrations showing the variety of uses we make of the terms “forgetting” and “trying”, for these uses are closely connected with those of the word “can”. Consider || Contemplate these cases: a) Before, B had said to himself the formula, now, “He finds a complete blank there”. b) Before, he had said to himself the formula, now, for a moment he isn't sure “whether it was 2n or 3n”. c) He has forgotten a name and it is “on the tip of his tongue”. Or d), he is not certain whether he has ever known the name or has forgotten it.
Now look at the way in which we use the word “trying”: a) A man is trying to open a door by pulling as hard as he can. b) He is trying to open the door of a safe by trying to find the combination. c) He is trying to find the combination by trying to remember it, or d) by turning the knobs and listening with a stethoscope. Consider the various processes we call “trying to remember”. Compare e) trying to move your finger against a resistance (e.g. when someone is holding it), and f) when you have intertwined the fingers of both hands in a particular way and feel “You don't know what to do in order to make a particular finger move”.
(Consider also the class of cases in which we say, “I can do so-and-so but I won't”: “I could if I tried” – – e.g. lift 100 pounds; “I could if I wished” – – e.g. say the alphabet.)
One might perhaps suggest that the only case in which it is correct to say, without restriction, that I can do a certain
Template:BBB TS reference thing, is that in which while saying that I can do it, I actually do it, and that otherwise I ought to say, “I can do it as far as … is concerned”. One may be inclined to think that only in the above case has a person given a real proof of being able to do a thing.
). But if we look at a language-game in which the phrase “I can … ” is used in this way (e.g., a game in which doing a thing is taken as the only justification for saying that one is able to do it), we see that there is not the metaphysical difference between this game and one in which other justifications are accepted for saying “I can do so-and-so”. A game of the kind 65), by the way, shows us the real use of the phrase, “If something happens it certainly can happen”; an almost useless phrase in our language. It sounds as though it had some very clear and deep meaning, but like most of the general philosophical propositions it is meaningless except in very special cases.
). Make this clear to yourself by imagining a language (similar to 49)) which has two expressions for such sentences as, “I am lifting a fifty pound weight”; one expression is used whenever the action is performed as a test (say, before an athletic competition), the other expression is used when the action is not performed as a test.
We see that a vast net of family likenesses connects the cases in which the expressions of possibility, “can”, “to be able to”, etc. are used. Certain characteristic features, we may say, appear in these cases in different combinations: there is, e.g., the element of conjecture (that something will behave
Template:BBB TS reference in a certain way in the future); the description of the state of something (as a condition for its behaving in a certain way in the future); the account of certain tests someone or something has passed. ‒ ‒
There are, on the other hand, various reasons which incline us to look at the fact of something being possible, someone being able to do something, etc., as the fact that he or it is in a particular || peculiar state. Roughly speaking, this comes to saying that “A is in the state of being able to do something” is the form of representation we are most strongly tempted to adopt, or, as one could also put it, we are strongly inclined to use the metaphor of something being in a peculiar state for saying that something can behave in a particular way. And this way of representation, or this metaphor, is embodied in the expressions, “He is capable of … ”, “He is able to multiply large numbers in his head”, “He can play chess”: in these sentences the verb is used in the present tense, suggesting that the phrases are descriptions of states which exist at the moment when we speak.
The same tendency shows itself in our calling the ability of solving a mathematical problem, the ability to enjoy a piece of music, etc., certain states of the mind; we don't mean by this expression “conscious mental phenomena”. Rather, a state of the mind in this sense is the state of a hypothetical mechanism, a mind model meant to explain the conscious mental phenomena. (Such things as unconscious or subconscious mental states are features of the mind model.) In this way also we
Template:BBB TS reference can hardly help conceiving of memory as of a kind of storehouse. Note also how sure people are that to the ability of adding or multiplying or to that of saying a poem by heart, etc., there must correspond a peculiar state of the person's brain, although on the other hand they know next to nothing about such psycho-physiological correspondences. We have an overwhelmingly strong tendency to conceive of the phenomena which in such || these cases we actually observe by the symbol of a mechanism whose manifestations these phenomena are; We regard these phenomena as manifestations of this mechanism. and their possibility is the particular construction of the mechanism itself.
Now looking back to our discussion of 43), we see that it was no final || real explanation of B's being guided by the signs when we said that B was guided if he could also have carried out orders consisting in other combinations of dots and dashes than those of 43). In fact, when we considered the question whether B in 43) was guided by the signs, we were all the time inclined to say some such thing as that we could only decide this question with certainty if we could look into the actual mechanism connecting seeing the signs with acting according to them. For we have a definite picture of what in a mechanism we should call certain parts being guided by others. In fact, the mechanism which immediately suggests itself when we wish to show what in such a case as 43) we should call “being guided by the signs” is a mechanism of the type of a pianola. Here, in the working of the pianola we have a clear case of certain actions,
Template:BBB TS reference those of the hammers of the piano, being guided by the pattern of holes in the pianola roll. We could use the expression, “The pianola is reading off the record made by the perforations in the roll”, and we might call patterns of such perforations complex signs or sentences, opposing their function in a pianola to the function which similar devices have in mechanisms of a different type, e.g., the combination of notches and teeth which form a key bit. The bolt of a lock is caused to slide by this particular combination, but we should not say that the movement of the bolt was guided by the way in which we combined teeth and notches, i.e., we should not say that the bolt moved according to the pattern of the key bit. You see here the connection between the idea of being guided and the idea of being able to read new combinations of signs: for we should say that the pianola can read any pattern of perforations, of a particular kind, it is not built for one particular tune or set of tunes (like a musical box), – – whereas the bolt of the lock reacts to that pattern of the key bit only which is predetermined in || by the construction of the lock. We could say that the notches and teeth forming a key bit are not comparable to the words making up a sentence but to the letters making up a word, and that the pattern of the key bit in this sense did not correspond to a complex sign, to a sentence, but to a word.
It is clear that although we might use the ideas of such mechanisms as similes for describing the way in which B acts in the games 42) and 43), no such mechanisms are actually involved in these games. We shall have to say that the use which we
Template:BBB TS reference made of the expression “to be guided” in our examples of the pianola and of the lock is only one use within a family of usages, though these examples may serve as metaphors, ways of representation, for other usages.
Let us study the use of the expression, “to be guided”, by studying the use of the word “reading”. By “reading” I here mean the activity of translating script into sounds, also of writing according to dictation or of copying in writing a page of print, and such like; reading in this sense does not involve any such thing as understanding what you read. The use of the word “reading” is, of course, extremely familiar to us in the circumstances of our ordinary life (it would be extremely difficult to describe these circumstances even roughly). A person, say an Englishman, has as a child gone through one of the normal ways of training in school or at home, he has learned to read his language, later on he reads books, newspapers, letters, etc. What happens when he reads the newspaper? ‒ ‒ His eyes glide along the printed words, he pronounces them aloud or to himself, but he pronounces certain words just taking their pattern in as a whole, other words which he pronounces after having seen their first few letters only, others again he reads out letter by letter. We should also say that he had read a sentence if while letting his eyes glide along it he had said nothing aloud or to himself, but on being asked afterwards what he had read he was able to reproduce the sentence verbatim or in slightly different words. He may also act as what we might call a mere reading machine, I mean, paying no attention to
Template:BBB TS reference what he spoke, perhaps concentrating his attention on something totally different. We should in this case say that he read if he acted faultlessly like a reliable machine. ‒ ‒ Compare with this case the case of a beginner. He reads the words by spelling them out painfully. Some of the words however, he just guesses from their contexts, or possibly he knows the piece by heart. The teacher then says that he is pretending to read the words, or just that he is not really reading them. If, looking at this example, we asked ourselves what reading was, we should be inclined to say that it was a particular conscious mental act. This is the case in which we say, “Only he knows whether he is reading; nobody else can really know it”. Yet we must admit that as far as the reading of a particular word goes, exactly the same thing might have happened in the beginner's mind when he “pretended” to read as what happened in the mind of the fluent reader when he read the word. We are using the word “reading” in a different way when we talk about the accomplished reader on the one hand and the beginner on the other hand. What in the one case we call an instance of reading we don't call an instance of reading in the other. ‒ ‒ Of course we are inclined to say that what happened in the accomplished reader and in the beginner when they pronounced the word could not have been the same. The difference lying, if not in their conscious states, then in the unconscious regions of their minds, or in their brains. We here imagine two mechanisms, the internal working of which we can see, and this internal working is the real criterion for a person's reading or not
Template:BBB TS reference reading. But in fact no such mechanisms are known to us in these cases. Look at it in this way:
). Imagine that human beings or animals were used as reading machines, assume that in order to become reading machines they need a particular training. The man who trains them says of some of them that they already can read, of others that they can't. Take a case of one who has so far not responded to the training. If you put before him a printed word he will sometimes make sounds, and every now and then it happens “accidentally” that these sounds more or less agree with || correspond to the printed word. A third person hears the pupil || creature under training uttering the right sound on looking at the word “table”. The third person says, “He reads”, but the teacher answers, “No, he doesn't, it is mere accident”. But supposing now that the pupil on being shown other words and sentences goes on reading them correctly. After a time the teacher says, “Now he can read”. ‒ ‒ But what about the first word “table”? Should the teacher say, “I was wrong; he read that, too”, or should he say, “No, he only started reading later”? When did he really begin to read, or: Which was the first word, or the first letter, which he read? It is clear that this question here makes no sense unless I give an “artificial” explanation such as: “The first word which he reads = the first word of the first hundred consecutive words he reads correctly”. ‒ ‒ Suppose on the other hand that we used the word “reading” to distinguish between the case when a particular conscious process of spelling out the words takes place in a person's mind from the case in which this does not happen:
– – Then, at least the person who is reading could say that such-and-such a word was the first which he actually read. ‒ ‒ Also, in the different case of a reading machine which is a mechanism connecting signs with the reactions to these signs, e.g., a pianola, we could say, “only after such-and-such a thing has been done to the machine, e.g., certain parts had been connected by wires, the machine actually read; the first letter which it read was a d”. ‒ ‒
In the case 67), by calling certain creatures “reading machines” we meant only that they react in a particular way to seeing printed signs. No connection between seeing and reacting, no internal mechanism enters into this case. It would be absurd if the trainer had answered to the question whether he read the word “table” or not, “Perhaps he read it”, for there is no doubt in this case about what he actually did. The change which took place was one which we might call a change in the general behaviour of the pupil, and we have in this case not given a meaning to the expression, “The first word in the new era”. (Compare with this the following case:
∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙ ∙
In our figure a row of dots with large intervals succeeds a row of dots with small intervals. Which is the last dot in the first sequence and which the first dot in the second? Imagine our dots were holes in the revolving disc of a siren. Then we should hear a tone of low pitch following a tone of high pitch (or vice versa). Ask yourself: At which moment does the tone of low pitch begin and the other end?)
Template:BBB TS reference There is a great temptation on the other hand to regard the conscious mental act as the only real criterion distinguishing reading from not reading. For we are inclined to say, “Surely a man always knows whether he is reading or pretending to read”, or “Surely a man always knows when he is really reading”. If A tries to make B believe that he is able to read Cyrillic script, cheating him by learning a Russian sentence by heart and then saying it while looking at the printed sentence, we may certainly say that A knows that he is pretending and that he is not reading in this case is characterized by a particular personal experience, namely, that of saying the sentence by heart. Also, if A makes a slip in saying it by heart, this experience will be different from that which a person has who makes a slip in reading.
). But supposing now that a man who could read fluently and who was made to read sentences which he had never read before read these sentences, but all the time with the peculiar feeling of knowing the sequence of words by heart. Should we in this case say that he was not reading, i.e., should we regard his personal experience as the criterion distinguishing between reading and not reading?
). Or imagine this case: A man under the influence of a certain drug is shown a group of five signs, not letters of an existing alphabet; and looking at them with all the outward signs and personal experiences of spelling out a word, pronounces the word “ABOVE”. (This sort of thing happens in dreams. After waking up we then say, “It seemed to me that I was reading these
Template:BBB TS reference signs though they weren't really signs at all”.) In such a case some people might be inclined to say that he is reading, others that he isn't. We could imagine that after he had spelt out the word “above” we showed him other combinations of the five signs and that he read them consistently with his reading of the first permutation of signs shown to him. By a series of similar tests we might find that he used what we might call an imaginary alphabet. If this was so, we should be more ready to say, “He reads” than “He imagines that he reads, but he doesn't really”.
Note also that there is a continuous series of intermediary cases between the case when a person knows by heart what is in print before him and the case in which he spells out the letters of every word without any such help as guessing from the context, knowing by heart, and such like.
Do this: Say by heart the series of cardinals from one to twelve, – – Now look at the dial of your watch and read this sequence of numbers. Ask yourself what in this case you called reading, that is, what did you do to make it reading?
Let us try this explanation: A person reads if he derives the copy which he is producing from the model which he is copying. (I will use the word “model” to mean that which he is reading off, e.g., the printed sentences which he is reading or copying in writing, or such signs as “--..-” in 42) and 43) which he is “reading” by his movements, or the scores which a pianist plays off, etc. The word “copy” I use for the sentence spoken or written from the printed one, for the movements made
Template:BBB TS reference according to such signs as “--..-”, for the movements of the pianist's fingers or the tune which he plays from the scores, etc.) Thus if we had taught a person the Cyrillic alphabet and had taught him how each letter was pronounced, if then we gave him a piece printed in the Cyrillic script and he spelt it out according to the pronunciation of each letter as we had taught it, we should undoubtedly say that he was deriving the sound of every word from the written and spoken alphabet taught him. And this also would be a clear case of reading. (We might use the expression, “We have taught him the rule of the alphabet”.)
But, let us see, what made us say that he derived the spoken words from the printed by means of the rule of the alphabet? Isn't all we know that we told him that this letter was pronounced this way, that letter that way, etc., and that he afterwards read out words in the Cyrillic script? What suggests itself to us as an answer is that he must have shown somehow that he did actually make the transition from the printed to the spoken words by means of the rule of the alphabet which we had given him. And what we mean by his showing this will certainly get clearer if we alter our example and
). assume that he reads off a text by transcribing it, say, from block letters into cursive script. For in this case we can assume the rule of the alphabet to have been given in the form of a table which shows the block alphabet and the cursive alphabet in parallel columns. Then the deriving the copy from the text we should imagine this way: The person who copies looks
Template:BBB TS reference up the table for each letter at frequent intervals, or he says to himself such things as, “Now what's a small a like?”, or he tries to visualize the table, refraining from actually looking at it. ‒ ‒
). But what if, doing all this, he then transcribed an “A” into a “b”, a “B” into a “c”, and so on? Should we not call this “reading” “deriving” too? We might in this case describe his procedure by saying that he used the table as we should have used it had we not looked straight from left to right like this: but like this: though he actually when looking up the table passed with his eyes or finger horizontally from left to right. ‒ ‒ But let us suppose now
). that going through the normal processes of “looking up”, he transcribed an “A” into an “n”, a “B” into an “x”, in short, acted, as we might say, according to a scheme of arrows which showed no simple regularity. Couldn't we call this “deriving” too? ‒ ‒ But suppose that
). he didn't stick to this way of transcribing. In fact he changed it, but according to a simple rule: After having transcribed “A” into “n”, he transcribed the next “A” into “o”, and the next “A” into “p”, and so on. But where is the sharp line between this procedure and that of producing a transcription without any system at all? Now you might object to this by saying, “In the case 71), you obviously assumed that he understood the table differently; he didn't understand it in the normal way”. But what do we call “understanding the table in
Template:BBB TS reference a particular way?” But whatever process you imagine this “understanding” to be, it is only another link interposed between the outward and inward processes of deriving || derivation I have described and the actual transcription. In fact this process of understanding could obviously be described by means of a schema of the kind used in 71), and we could then say that in a particular case he looked up the table like this: ; understood the table like this: ; and transcribed it like this: . But does this mean that the word “deriving” (or “understanding”) has really no meaning, as by following up its meaning this seems to trail off into nothing? In case 70) the meaning of “deriving” stood out quite clearly, but we told ourselves that this was only one special case of deriving. It seemed to us that the essence of the process of deriving was here presented in a particular dress and that by stripping it of this we should get at the essence. Now in 71), 72), 73) we tried to strip our case of what had seemed but its peculiar costume only to find that what had seemed mere costumes were the essential features of the case. (We acted as though we had tried to find the real artichoke by stripping it of its leaves.) The use of the word “deriving” is indeed exhibited in 70), i.e., this example showed us one of the family of cases in which this word is used. And the explanation of the use of this word, as that of the use of the word “reading” or “being guided by symbols”, essentially consists in describing a selection of examples exhibiting characteristic features, some examples showing these
Template:BBB TS reference features in exaggeration, others showing transitions, || exaggerated form, others in transitional phases, certain series of examples showing the trailing off of such features. Imagine that someone wished to give you an idea of the facial characteristics of a certain family, the So-and-so's, he would do it by showing you a set of family portraits and by drawing your attention to certain characteristic features, and his main task would consist in the proper arrangement of these pictures, which, e.g., would enable you to see how certain influences gradually changed the features, in what characteristic ways the members of the family aged, what features appeared more strongly as they did so.
It was not the function of our examples to show us the essence of “deriving”, “reading”, and so forth through a veil of inessential features; they || the examples were not descriptions of an outside letting us guess at an inside which for some reason or other could not be shown in its nakedness. We are tempted to think that our examples are indirect means for producing a certain image or idea in a person's mind, – – that they hint at something which they cannot show. This would be so in some such case as this: Suppose I wish to produce in someone a mental image of the inside of a particular 18th century room which he is prevented from entering. I therefore adopt this method: I show him the house from the outside, pointing out the windows of the room in question, I further lead him into other rooms of the same period. ‒ ‒
Our method is purely descriptive; the descriptions we give are not hints of explanations.