Tractatus Logico-Philosophicus (português): Difference between revisions
No edit summary |
No edit summary |
||
| Line 1,481: | Line 1,481: | ||
E não há coisa no ''campo visual'' que leve à conclusão de que ela é vista por um ôlho. | E não há coisa no ''campo visual'' que leve à conclusão de que ela é vista por um ôlho. | ||
'''5.6331''' O campo visual não tem nomeadamente uma forma como esta:[[File:TLP 5. | '''5.6331''' O campo visual não tem nomeadamente uma forma como esta:[[File:TLP 5.6331pt.png|250px|center|link=]]'''5.634''' Isto se liga a que nenhuma parte de nossa experiência é ''a priori''. | ||
Tudo o que vemos poderia ser diferente. | Tudo o que vemos poderia ser diferente. | ||
| Line 1,501: | Line 1,501: | ||
Esta é a forma geral da proposição. | Esta é a forma geral da proposição. | ||
'''6.001''' Isto nada mais diz do que: cada proposição resulta da aplicação sucessiva da operação <math>N (\bar{\xi})</math> sôbre as proposições elementares.<references /> | '''6.001''' Isto nada mais diz do que: cada proposição resulta da aplicação sucessiva da operação <math>N (\bar{\xi})</math> sôbre as proposições elementares. | ||
'''6.002''' Dada a forma geral de como construir uma proposição, com isto já está dada a forma geral de como é possível gerar outra, por meio de uma operação, partindo-se de uma proposição. | |||
'''6.01''' A forma geral da operação <math>\Omega ' (\bar{\eta})</math> é pois: <math>[\bar{\xi}, N(\bar{\xi})]' (\bar{\eta}) (= [ \bar{\eta}, \bar{\xi}, N (\bar{\xi}) ])</math>. | |||
Esta é a forma mais geral da transposição de uma proposição para outra. | |||
'''6.02''' Chegamos ''assim'' aos números. Defino: | |||
{{p center|<math>x = \Omega^{0 \prime} x \text{ Def.}</math> e<br> | |||
<math>\Omega^{\prime} \Omega^{ \nu \prime} x = \Omega^{ \nu + 1 \prime} x \text{ Def.}</math>}} | |||
Segundo essa regra de signos, escrevemos pois a série: <math>x, \Omega ' x, \Omega ' \Omega ' x, \Omega ' \Omega ' \Omega ' x, .....</math> | |||
{{p center|como: <math>\Omega^{0 \prime} x, \Omega^{0+1 \prime} x, \Omega^{0 + 1 + 1 \prime} x, \Omega^{0 + 1 + 1 + 1 \prime} x, .....</math>}} | |||
Em vez de "<math>[ x, \xi, \Omega ' \xi ]</math>" escrevo, portanto, | |||
{{p center|"<math>[ \Omega^{0 \prime} x, \Omega^{ \nu \prime} x, \Omega^{ \nu + 1 \prime} x ]</math>".}} | |||
E defino: | |||
{{p indent|<math>0 + 1 = 1 \text{ Def.}</math>}} | |||
{{p indent|<math>0 + 1 + 1 = 2 \text{ Def.}</math>}} | |||
{{p indent|<math>0 + 1 + 1 + 1 = 3 \text{ Def.}</math>}} | |||
{{p indent|(e assim por diante)}} | |||
'''6.021''' O número é o expoente de uma operação. | |||
'''6.022''' O conceito de número nada mais é do que é comum a todos os números, a forma geral do número. O conceito número é a variável número. | |||
E o conceito da igualdade entre os números é a forma geral de todas as igualdades especiais entre os números. | |||
'''6.03''' A forma geral dos números inteiros é: [0, ''ξ'', ''ξ''+1]. A teoria das classes é inteiramente supérflua para a matemática. | |||
Isto está ligado a que a universalidade de que precisamos na matemática não é a ''acidental''. | |||
'''6.1''' As proposições da lógica são tautologias.<references /> | |||
Revision as of 16:28, 26 December 2023
A memória de
David H. Pinsent
Mote: ... e tudo o que se sabe, que não seja apenas rumor ouvido, pode ser dito em três palavras.
Kürnberger
Prefácio
Talvez êste livro sòmente seja compreendido por quem já tenha cogitado por si próprio os pensamentos aqui expressos, ou ao menos cogitado pensamentos semelhantes. Não é, pois, um manual. Terá alcançado seu objetivo se agradar a quem o ler com atenção.
Trata de problemas filosóficos e mostra, creio eu, que o questionar dêsses problemas repousa na má compreensão da lógica de nossa linguagem. Poder-se-ia apanhar todo o sentido do livro com estas palavras: em geral o que pode ser dito, o pode ser claramente, mas o que não se pode falar deve-se calar.
Pretende, portanto, estabelecer um limite ao pensar, ou melhor, não ao pensar mas à expressão do pensamento, porquanto para traçar um limite ao pensar deveríamos poder pensar ambos os lados dêsse limite (de sorte que deveríamos pensar o que não pode ser pensado).
O limite será, pois, traçado únicamente no interior da lingua; tudo o que fica além dêle será simplesmente absurdo.
Não quero julgar até onde meus esforços coincidem com os de outros filósofos. Por certo o que escrevi não pretende ser original no pormenor; por isso não dou fonte alguma, pôsto que me é indiferente se o que pensei já foi pensado por alguém antes de mim.
Quero apenas mencionar que devo grande parte do estímulo a meus pensamentos às grandiosas obras de Frege e aos trabalhos de meu amigo Sr. Bertrand Russell.
Caso meu trabalho tenha valor, êle será duplo. Primeiramente porque exprime pensamentos, valor que será tanto maior quanto melhor os pensamentos forem expressos. Nisto estou consciente de estar muito aquém do possível, simplesmente porque minhas forças são poucas para cumprir a tarefa. Possam outros vir e fazer melhor.
No entanto, a verdade dos pensamentos comunicados aqui me parece intocável e definitiva, de modo que penso ter resolvido os problemas no que é essencial. Se não me engano, o segundo valor dêsse trabalho é mostrar quão pouco se consegue quando se resolvem tais problemas.
Viena, 1918
L. W.
1[1] O mundo é tudo o que ocorre.
1.1 O mundo é a totalidade dos fatos, não das coisas.
1.11 O mundo é determinado pelos fatos e por isto consistir em todos os fatos.
1.12 A totalidade dos fatos determina, pois, o que ocorre e também tudo que não ocorre.
1.13 Os fatos, no espaço lógico, são o mundo. O mundo se resolve em fatos...
1.2 Algo pode ocorrer ou não ocorrer e todo o resto permanecer na mesma.
2 O que ocorre, o fato, é o subsistir dos estados de coisas.
2.01 O estado de coisas é uma ligação de objetos (coisas).
2.011 É essencial para a coisa poder ser parte consti- tuinte de um estado de coisas.
2.012 Nada é acidental na lógica: se uma coisa puder aparecer num estado de coisas, a possibilidade do estado de coisas já deve estar antecipada nela.
2.0121 Parece, por assim dizer, acidental que à coisa, que poderia subsistir sozinha e para si, viesse ajus- tar-se em seguida uma situação..
Se as coisas podem aparecer em estados de coisas, então isto já deve estar nelas.
(Algo lógico não pode ser meramente-possível. A lógica trata de cada possibilidade e todas as possibilidades são fatos que lhe pertencem.)
Assim como não podemos pensar objetos espaciais fora do espaço, os temporais fora do tempo, assim não podemos pensar nenhum objeto fora da possibilidade de sua ligação com outros.
Se posso pensar o objeto ligando-o ao estado de coisas, não posso então pensá-lo fora da possibilidade dessa ligação.
2.0122 A coisa é autônoma enquanto puder aparecer em tôdas as situações possíveis, mas esta forma de autonomia é uma forma de conexão com o estado de coisas, uma forma de heteronomia. (É impossível palavras comparecerem de dois modos diferentes, sòzinhas e na proposição.)
2.0123 Se conheço o objeto, também conheço tôdas as. possibilidades de seu aparecer em estados de coisas.
(Cada uma dessas possibilidades deve estar na natureza do objeto.)
Não é possível posteriormente encontrar nova possibilidade.
2.01231 Para conhecer um objeto não devo com efeito conhecer suas propriedades externas — mas todas as internas.
2.0124 Ao serem dados todos os objetos, dão-se também todos os possíveis estados de coisas.
2.013 Cada coisa está como num espaço de estados de coisas possíveis. Posso pensar êste espaço vazio, mas não a coisa sem o espaço.
2.0131 O objeto espacial deve estar no espaço infinito. (O ponto no espaço é lugar do argumento.)
A mancha no campo visual não deve, pois, ser vermelha, mas deve ter uma côr; tem; por assim dizer, uma espacialidade colorida em volta de si. O som deve possuir uma altura, o objeto do tato, uma dureza, e assim por diante.
2.014 Os objetos contêm a possibilidade de todas as situações.
2.0141 A possibilidade de seu aparecer nos estados de coisas é a forma dos objetos.
2.02 O objeto é simples.
2.0201 Cada asserção sobre complexos deixa-se dividir numa asserção sobre suas partes constitutivas e naquelas proposições que descrevem inteiramente tais complexos.
2.021 Os objetos formam a substância do mundo. Por isso não podem ser compostos.
2.0211 Se o mundo não possuísse substância, para uma proposição ter sentido dependeria de outra proposição ser verdadeira.
2.0212 Seria, pois, impossível traçar uma figuração do mundo (verdadeira ou falsa).
2.022 É claro que um mundo, pensado muito diferente do real, deve possuir algo — uma forma — comum com êste mundo real.
2.023 Esta forma fixa consiste precisamente em objetos.
2.0231 A substância do mundo pode determinar apenas uma forma, mas não propriedades materiais; já que estas são primeiramente representadas pelas proposições — primeiramente formadas pela configuração dos objetos.
2.0232 Aproximadamente falando: os objetos são desprovidos de côr.
2.0233 Dois objetos de mesma forma lógica — abstraindo suas propriedades externas — se diferenciam um do outro apenas por serem distintos.
2.02331 Ou uma coisa possui propriedades que nenhuma outra possui e dêsse modo é possível sem mais separá- la de outras por uma descrição e referir-se a ela; ou, ao contrário, existem várias coisas que possuem tôdas suas propriedades em comum, sendo então impossível em geral indicar uma delas.
Se a coisa não se distingue por nada, não posso então distingui-la, pois do contrário estaria distinguida.
2.024 Substância é o que subsiste independentemente do que ocorre.
2.025 Ela é forma e conteúdo.
2.0251 Espaço, tempo e côr (coloridade) são formas dos objetos.
2.026 Só se houver objetos, pode haver forma fixa do mundo.
2.027 O fixo, o subsistente e o objeto são um só.
2.0271 O objeto é o fixo, o subsistente; a configuração é o mutável, o instável.
2.0272 A configuração dos objetos forma o estado de coisas.
2.03 No estado de coisas os objetos se ligam uns aos outros como elos de uma cadeia.
2.031 No estado de coisas os objetos estão uns em relação aos outros de um modo determinado.
2.032 O modo pelo qual os objetos se vinculam no estado de coisas constitui a estrutura do estado de coisas.
2.033 A forma é a possibilidade da estrutura.
2.034 A estrutura do fato é constituída pelas estruturas dos estados de coisas.
2.04 A totalidade dos subsistentes estados de coisas é o mundo.
2.05 A totalidade dos subsistentes estados de coisas determina também quais estados de coisas não subsistem.
2.06 A subsistência e a não-subsistência dos estados de coisas é a realidade.
(Chamamos de fato positivo à subsistência de estados de coisas e de negativo à não-subsistência dėles.)
2.061 Os estados de coisas são independentes uns dos outros.
2.062 Da subsistência ou da não-subsistência de um estado de coisas não é possível concluir a subsistência ou a não-subsistência de outro.
2.063 A realidade inteira é o mundo.
2.1 Fazemo-nos figurações dos fatos.
2.11 A figuração presenta a situação no espaço lógico, a subsistência e a não-subsistência de estados de coisas.
2.12 A figuração é um modelo da realidade.
2.13 Na figuração, seus elementos correspondem aos objetos.
2.131 Os elementos da figuração substituem nela os objetos.
2.14 A figuração consiste em que seus elementos estão uns em relação aos outros de um modo determinado.
2.141 A figuração é um fato.
2.15 Os elementos da figuração estando uns em relação aos outros de um modo determinado, isto representa as coisas estando umas em relação às outras.
Esta vinculação dos elementos da figuração chama-se sua estrutura e a possibilidade dela, sua forma de afiguração.
2.151 A forma de afiguração é a possibilidade de que as coisas estejam umas em relação às outras como os elementos da figuração.
2.1511 A figuração enlaça-se com a realidade; dêste modo: estendendo-se para ela.
2.1512 É como padrão de medida que se aplica à realidade.
2.15121 Somente os pontos mais exteriores das linhas divisórias tocam o objeto a ser medido.
2.1513 Segundo essa concepção, também pertence à figuração a forma afigurante que precisamente a torna figuração.
2.1515 A relação afigurante consiste nas coordenações dos elementos da figuração e das coisas.
2.1515 Estas coordenações são, por assim dizer, antenas dos elementos da figuração, com as quais esta toca a realidade.
2.16 Os fatos, para serem figuração, devem ter algo em comum com o que é afigurado.
2.161 Deve haver algo idêntico na figuração e no afigurado a fim de que um possa ser a figuração do
outro.
2.17 O que a figuração realidade para poder correta ou falsamente deve ter em comum com a afigurar à sua maneira é sua forma de afiguração.
2.171 A figuração pode afigurar qualquer realidade cuja forma ela possui.
A figuração espacial, tudo o que é espacial; a colorida, tudo que é colorido, etc.
2.172 Sua forma de afiguração, contudo, a figuração não pode afigurar; apenas a exibe.
2.173 A figuração representa seu objeto de fora (seu ponto de vista é sua forma de representação), por isso a figuração representa seu objeto correta ou falsamente.
2.174 A figuração não pode, porém, colocar-se fora de sua forma de representação.
2.18 O que cada figuração, de forma qualquer, deve sempre ter em comum com a realidade para poder afigurá-la em geral - correta ou falsamente - é a forma lógica, isto é, a forma da realidade.
2.181 Se a forma da afiguração é a forma lógica, a figuração chama-se lógica.
2.182 Tôda figuração também é lógica. (No entanto, nem tôda figuração é, por exemplo, espacial.)
2.19 A figuração lógica pode afigurar o mundo.
2.2 A figuração tem em comum com o afigurado a forma lógica da afiguração.
2.201 A figuração afigura a realidade, pois representa uma possibilidade da subsistência e da não-subsistência de estados de coisas.
2.202 A figuração representa uma situação possível no espaço lógico.
2.203 A figuração contém a possibilidade da situação, a qual ela representa.
2.21 A figuração concorda ou não com a realidade, é correta ou incorreta, verdadeira ou falsa.
2.22 A figuração representa o que representa, independentemente de sua verdade ou falsidade, por meio da forma da afiguração.
2.221 O que a figuração representa é o seu sentido.
2.222 Na concordância ou na discordância de seu sentido com a realidade consiste sua verdade ou sua falsidade.
2.223 Para reconhecer se uma figuração é verdadeira ou falsa devemos compará-la com a realidade.
2.224 Não é possível reconhecer apenas pela figuração se ela é verdadeira ou falsa.
2.225 Não existe uma figuração a priori verdadeira.
3 Pensamento é a figuração lógica dos fatos.
3.001 "Um estado de coisas é pensável" significa: podemos construir-nos uma figuração dêle.
3.01 A totalidade dos pensamentos verdadeiros figuração do mundo.
3.02 O pensamento contém a possibilidade da situação que êle pensa. O que é pensável também é possível.
3.03 Não podemos pensar nada ilógico, porquanto, do contrário, deveríamos pensar ilògicamente.
3.031 Já foi dito por alguém que Deus poderia criar tudo, salvo o que contrariasse as leis lógicas. Isto porque não podemos dizer como pareceria um mundo "ilógico".
3.032 Representar na linguagem algo que "contrarie as leis lógicas" é tão pouco possível como representar, na geometria, por meio de suas coordenadas, uma figura que contrarie as leis do espaço; ou, então, dar as coordenadas de um ponto inexistente.
3.0321 Podemos perfeitamente representar um estado de coisas espacial contrário às leis da física, nunca, porém, contrário às leis da geometria.
3.04 Um pensamento correto a priori seria aquêle cuja possibilidade condicionasse sua verdade.
3.05 Desse modo, só poderíamos conhecer a priori que um pensamento é verdadeiro se a verdade dêle fosse reconhecível a partir do próprio pensamento (sem objeto de comparação).
3.1 Na proposição o pensamento se exprime sensível e perceptivelmente.
3.11 Utilizamos o signo sensível e perceptível (signo sonoro ou escrito, etc.) da proposição como projeção da situação possível.
O método de projeção é o pensar do sentido da proposição.
3.12 Chamo signo proposicional o signo pelo qual exprimimos o pensamento. E a proposição é o signo proposicional em sua relação projetiva com o mundo.
3.13 A proposição pertence tudo que pertence à projeção, não, porém, o que é projetado.
Portanto, a possibilidade do que é projetado, não, porém, êste último.
A proposição, portanto, não contém seu sentido, mas a possibilidade de exprimi-lo.
("O conteúdo da proposição" quer dizer o conteúdo da proposição significativa.)
Está contida na proposição a forma de seu sentido, não, porém, seu conteúdo.
3.14 O signo proposicional consiste em que seus elementos, as palavras, estão relacionados uns aos outros de maneira determinada.
O signo proposicional é um fato.
3.141 A proposição não é uma mistura de palavras. (Do mesmo modo que o tema musical não é uma mistura de sons.)
A proposição é articulada.
3.142 Sòmente fatos podem exprimir um sentido, uma classe de nomes não o pode.
3.143 Que um signo proposicional seja um fato, isto é velado pela forma comum de expressão, escrita ou impressa.
Na proposição impressa, por exemplo, o signo proposicional não parece essencialmente diferente da palavra.
(Foi assim possível a Frege chamar à proposição de nome composto.)
3.1431 A essência do signo proposicional se torna muito clara quando, em vez de o pensarmos composto de signos escritos, o pensamos composto de objetos espaciais (tais como mesas, cadeiras, livros).
A posição espacial oposta dessas coisas exprime, pois, o sentido da proposição.
'3.1432 Não: "O signo complexo aRb' diz que a por R se relaciona com b", mas: que "a" por um certo R se relaciona com "b", isto quer dizer que aRb.
3.144 É possível descrever situações, impossível no entanto nomeá-las.
(Os nomes são como pontos, as proposições, flechas; possuem sentido.)
3.2 Nas proposições os pensamentos podem ser expressos de tal modo que aos objetos dos pensamentos correspondam elementos do signo proposicional.
3.201 A êsses elementos chamo de "signos simples" e à proposição, "completamente analisada".
3.202 Os signos simples empregados nas proposições são chamados nomes.
3.203 O nome denota o objeto. O objeto é sua denotação. ("A" é o mesmo signo que "A".)
3.21 À configuração dos signos simples no signo proposicional corresponde a configuração dos objetos na situação.
3.22 Na proposição o nome substitui o objeto.
3.221 Posso nomear apenas objetos. Os signos os substituem. Posso apenas falar sobre êles, não posso, porém, enunciá-los. Uma proposição pode apenas dizer como uma coisa é, mas não o que é.
3.23 Postular a possibilidade de signos simples é postular a determinabilidade do sentido.
3.24 A proposição que trata de um complexo achase numa relação interna com a proposição que trata das partes constituintes dêle.
O complexo só pode ser dado por sua descrição, e esta concordará ou não concordará com êle. A proposição que se ocupa de um complexo inexistente não será absurda, mas simplesmente falsa.
Que um elemento proposicional designa um complexo, isto pode ser visto graças a uma indeterminabilidade na proposição na qual êle aparece. Sabemos por esta proposição que nem tudo está determinado. (A designação da universalidade já contém, com efeito, uma protofiguração.)
A reunião dos símbolos de um complexo em um símbolo simples pode ser expressa por uma definição.
3.25 Existe apenas uma e uma única análise completa da proposição.
3.251 A proposição exprime o que é expresso de um modo determinado e dado claramente: A proposição é articulada.
3.26 O nome não é para ser desmembrado ademais por uma definição: é um signo primitivo.
3.261 Cada signo definido designa por sôbre os signos pelos quais é definido, e as definições mostram o caminho.
Dois signos, um signo primitivo e outro definido por signos primitivos, não podem designar pela mesma maneira. Nomes não podem ser decompostos por definições. (Nenhum signo isolado e autônomo possui denotação.)
3.262 O que no signo não vem expresso é indicado pela aplicação. O que os signos escondem, a aplicação exprime.
3.263 As denotações dos signos primitivos podem ser esclarecidas por elucidações. Elucidações são proposições que contêm os signos primitivos. Só podem, portanto, ser entendidas quando já se conhecem as denotações dêsses signos.
3.3 Só a proposição possui sentido; só em conexão com a proposição um nome tem denotação.
3.31 A cada parte da proposição que caracteriza um sentido chamo de expressão (símbolo).
(A própria proposição é uma expressão.)
A expressão é tudo que, sendo essencial para o sentido da proposição, as proposições podem ter em comum entre si.
A expressão caracteriza uma forma e um conteúdo.
3.311 A expressão pressupõe as formas de tôdas as proposições nas quais pode aparecer. Constitui a marca característica comum a uma classe de proposições.
3.312 Representa-se, pois, por intermédio da forma geral das proposições que a caracteriza.
E assim a expressão será, nesta forma, constante e todo o resto, variável.
3.313 A expressão será representada por uma variável, cujos valores são as proposições que contêm a expressão.
(No caso limite, a variável torna-se constante, a expressão, a proposição.)
A uma tal variável chamo de "variável proposicional".
3.314 A expressão tem denotação apenas na proposição. Cada variável pode ser concebida como variável proposicional.
(A variável nome também.)
3.315 Se transformarmos uma parte constituinte de uma proposição numa variável, existe então uma classe de proposições constituída por todos os valores da proposição variável assim resultante. Esta classe ainda depende em geral do que nós, segundo um ajuste arbitrário, chamamos partes da proposição. Se, no entanto, transformarmos todos aquêles signos, cujas denotações foram determinadas arbitra riamente, em variáveis, ainda continua a existir aquela classe. Esta, porém, não mais depende de qualquer ajuste, mas únicamente da natureza da proposição. Corresponde a uma forma lógica — a uma protofiguração lógica.
3.316 Fixam-se os valores que a variável proposicional deve tomar.
A fixação dos valôres é a variável.
3.317 A fixação dos valores das variáveis proposicionais consiste na indicação das proposições, as quais têm como marca característica comum a variável.
A fixação é uma descrição dessas proposições.
A fixação se ocupará, pois, únicamente dos símbolos, não se ocupando de sua denotação.
E para a fixação é essencial ser apenas uma descrição de símbolos, nada assertando sobre o designado. Como se dá a descrição da proposição é inessencial.
3.318 Concebo a proposição — do mesmo modo que Frege e Russell — como função das expressões que nela estão contidas.
3.32 O signo é o que no símbolo é sensivelmente perceptível.
3.321 Dois símbolos diferentes podem ter, pois, em comum o mesmo signo (escrito ou sonoro, etc.) — designam dêsse modo de diferentes maneiras.
3.322 A marca característica comum a dois objetos nunca pode indicar que os designamos com o mesmo signo, embora com diferentes modos de designação; porquanto o signo, sem dúvida, é arbitrário. Poderíamos, portanto, escolher dois signos diferentes, e onde permaneceria o que é comum na designação?
3.323 Na linguagem corrente amiúde acontece que a mesma palavra designa de modos diferentes — pertencendo, pois, a símbolos diferentes — ou ainda duas palavras, que designam de modos diferentes, são empregadas na proposição superficialmente da mesma maneira.
Assim a palavra "é" aparece como cópula, como sinal de igualdade e expressão da existência; "existir", enquanto verbo intransitivo do mesmo modo que "ir"; "idêntico", enquanto adjetivo: falamos a respeito de algo, mas também de que algo acontece.
(Na proposição "Rosa é rosa" ("Grün ist grün") — onde a primeira palavra é nome de pessoa e a última é adjetivo — ambas as palavras não têm apenas denotações diferentes, mas constituem símbolos diferentes.)
3.324 Nascem, assim, as confusões mais fundamentais (de que tôda a filosofia está plena).
3.325 Para evitar êsses erros devemos usar uma linguagem simbólica que os exclua, pois esta não empregará superficialmente o mesmo signo para símbolos diferentes, e não empregará signos, que designam de maneira diversa, do mesmo modo. Uma linguagem simbólica, portanto, que obedeça à gramática lógica — à sintase lógica.
(A ideografia de Frege, ou a de Russell, constitui uma tal linguagem que, no entanto, não elimina todos os erros.)
3.326 Para reconhecer o símbolo no signo deve-se atentar para seu uso significativo.
3.327 O signo determina uma forma lógica somente junto de sua utilização lógico-sintática.
3.328 Se um signo não tem serventia, então êle é desprovido de denotação. Este é o sentido do lema de Occam.
(Se tudo se passa como se um signo tivesse denotação, então êle a terá.)
3.33 Na sintaxe lógica a denotação de um signo não há de desempenhar papel algum, a sintaxe deve elaborar-se sem que surja a preocupação com a denotação, devendo pressupor apenas a descrição das expressões.
3.331 Feita esta observação, consideremos a Theory of types de Russell: o erro dêste se revela quando, ao elaborar as regras dos signos, teve de apelar para a denotação dêsses signos.
3.332 Nenhuma proposição pode assertar algo sôbre si mesma, pois o signo proposicional não pode estar contido em si mesmo (aí está tôda a Theory of types).
3.333 Uma função por isso não pode ser seu próprio argumento, pois o signo da função já contém a protofiguração de seu argumento, e não contém a si própria.
Tomemos, por exemplo, a função F(fx) podendo ser seu próprio argumento; haveria então uma proposição "F(F(fx))", em que a função externa F e a interna F teriam denotações diferentes; a interna tendo como forma ϕ(fx), a externa, ψ(ϕ(fx)). Ambas as funções têm em comum apenas a letra "F" que nada designa.
Isto se torna claro logo que, em vez de "F(F(u))", escrevemos "(∃ϕ) : F(ϕu) . ϕu = Fu".
Isto liquida o paradoxo de Russell.
3.334 As regras da sintaxe lógica devem ser entendidas de per si, desde que se saiba apenas como cada signo designa.
3.34 A proposição possui traços essenciais e acidentais.
Acidentais são os traços que derivam da maneira particular de produzir o signo proposicional; essenciais, aqueles que sozinhos tornam a proposição capaz de exprimir seu sentido.
3.341 É pois essencial na proposição o que é comum a todas as proposições que podem exprimir o mesmo sentido.
E do mesmo modo é em geral essencial no símbolo o que é comum a todos os símbolos que podem preencher o mesmo fim.
3.3411 Seria então possível dizer: o nome autêntico é aquilo que todos os símbolos que designam o objeto têm em comum. Daí resultaria paulatinamente que nenhuma composição é essencial para o nome.
3.342 Há com efeito em nossa notação algo arbitrário, mas o seguinte não o é: se determinarmos algo arbitràriamente, então algo a mais deve ocorrer. (Isto depende da essência da notação.)
3.3421 Um modo particular de designação pode ser desimportante, mas é sempre importante que seja um modo possível de designação. Esta é a situação na filosofia em geral: o singular se manifesta repetidamente como desimportante, mas a possibilidade de cada singular nos dá um esclarecimento sobre a essência do mundo.
3.343 Definições são regras para a tradução de uma linguagem a outra. Cada linguagem simbólica correta deve deixar-se traduzir numa outra segundo tais regras: isto é tudo o que elas têm em comum.
3.344 O que designa no símbolo é o que é comum a todos os símbolos pelos quais o primeiro pode ser substituído de acordo com as regras da sintaxe lógica.
3.441 É possível, por exemplo, exprimir do seguinte modo o que é comum a tôdas as notações para as funções de verdade: é-lhes comum, por exemplo, poderem ser substituídas pela notação "∼p" ("não p") e "p ∨ q" ("p ou q").
(Com isso se indica a maneira pela qual uma notação especialmente possível nos pode dar esclarecimentos gerais.)
3.3442 O signo do complexo não se divide pela análise arbitràriamente, de modo que sua divisão fôsse diferente em cada construção proposicional.
3.4 A proposição determina um lugar no espaço lógico. A existência dêsse espaço lógico é assegurada apenas pela existência das partes constitutivas, pela existência das proposições significativas.
3.41 O signo proposicional e as coordenadas lógicas: é isto o lugar lógico.
3.411 O lugar geométrico e o lógico concordam em que ambos consistem na possibilidade de uma existência.
3.42 Se bem que a proposição deva determinar apenas um lugar do espaço lógico, o espaço lógico inteiro já deve ser dado por ela.
(Em caso contrário, novos elementos — em coordenação — sempre se introduziriam por meio da negação, da soma lógica, do produto lógico, etc.)
(O andaime lógico em volta da figuração determina o espaço lógico. A proposição apanha o espaço lógico inteiro.)
3.5 O signo proposicional empregado e pensado é o pensamento.
4 O pensamento é a proposição significativa.
4.001 A totalidade das proposições é a linguagem.
4.002 O homem possui a capacidade de construir linguagens nas quais cada sentido se deixa exprimir, sem contudo pressentir como e o que cada palavra denota. — Assim se fala sem saber como os sons singulares são produzidos.
A linguagem corrente forma parte do organismo humano e não é menos complicada do que êle.
É humanamente impossível de imediato apreender dela a lógica da linguagem.
A linguagem veda o pensamento; do mesmo modo, não é possível concluir, da forma exterior da veste, a forma do pensamento vestido por ela, porquanto a forma exterior da veste não foi feita com o intuito de deixar conhecer a forma do corpo.
Os acordos silenciosos para entender a linguagem corrente são enormemente complicados.
4.003 A maioria das proposições e questões escritas sôbre temas filosóficos não são falsas mas absurdas. Por isso não podemos em geral responder a questões dessa espécie, apenas estabelecer seu caráter absurdo. A maioria das questões e das proposições dos filósofos se apóiam, pois, no nosso desentendimento da lógica da linguagem.
(São questões da seguinte espécie: o bem é mais ou menos idêntico do que a beleza?)
Não é, pois, de admirar que os mais profundos problemas não constituam propriamente problemas.
4.0031 Tôda filosofia é "crítica da linguagem". (Por certo, não no sentido de Mauthner). O mérito de Russell é ter mostrado que a forma aparentemente lógica da proposição não deve ser sua forma real.
4.01 A proposição é figuração da realidade.
A proposição é modêlo da realidade tal como a pensamos.
4.011 À primeira vista, a proposição — em particular tal como está impressa no papel — não parece ser figuração da realidade de que trata. Mas tampouco a escrita musical parece à primeira vista ser figuração da música, e nossa escrita fonética (letras), figuração da linguagem falada.
No entanto, essas linguagens simbólicas se manifestam, também no sentido comum, como figurações do que representam.
4.012 É óbvio que percebemos como figuração uma proposição da forma "aRb". Aqui o signo é òbviamente um símile do designado.
4.013 E quando entramos no que é essencial dessa figuratividade vemos que ela não é perturbada por aparentes irregularidades (como o emprego de ♯ e de ♭ na escrita musical).
Porquanto também essas irregularidades afiguram o que devem expressar, apenas de outra maneira.
4.014 O disco da vitrola, o pensamento e a escrita musicais, as ondas sonoras estão uns em relação aos outros no mesmo relacionamento existente entre a linguagem e o mundo.
A todos é comum a construção lógica.
(Como na estória dos dois jovens, seus dois cavalos e seus lírios. Num certo sentido, todos são um.)
4.0141 Que exista uma regra geral por meio da qual o músico possa apreender a sinfonia a partir da partitura, regra por meio da qual se possa derivar a sinfonia das linhas do disco e ainda, segundo a primeira regra, de novo derivar a partitura; nisto consiste propriamente a semelhança interna dessas figuras aparentemente tão diversas. E essa regra é a lei de projeção que projeta a sinfonia na linguagem musical. É a regra da tradução da linguagem musical para a linguagem do disco.
4.015 A possibilidade de todos êsses símiles, a figuratividade inteira de nosso modo de expressão, se apóia na lógica da afiguração.
4.016 Para compreender a essência da proposição, convém pensar na escrita hieroglífica que afigura os fatos que descreve.
E dela provém o alfabeto sem perder o que é essencial na afiguração.
4.02 Isto se vê ao entendermos o sentido do signo proposicional sem que êle nos tenha sido explicado.
4.021 A proposição é figuração da realidade; pois conheço a situação representada por ela quando entendo a proposição. E entendo a proposição sem que o sentido me seja explicado.
4.022 A proposição mostra seu sentido.
4.023 A proposição mostra, se fôr verdadeira, como algo está. E diz que isto está assim.
Por meio da proposição a realidade deve ser fixada enquanto sim ou enquanto não.
Por isso deve ser completamente descrita por ela.
A proposição é a descrição de um estado de coisas.
Assim como a descrição de um objeto se dá segundo suas propriedades externas, a proposição descreve a realidade segundo suas propriedades internas.
A proposição constrói o mundo com a ajuda de andaimes lógicos, e por isso é possível, na proposição, também se ver, caso ela fôr verdadeira, como tudo que é lógico está. Pode-se de uma proposição falsa tirar conclusões.
4.024 Compreender uma proposição é saber o que ocorre, caso ela fôr verdadeira.
(É possível, pois, compreendê-la sem saber se é verdadeira.)
Ela será compreendida, caso se compreenda suas partes constituintes.
4.025 A tradução de uma linguagem para outra não se dá como se se traduzisse cada proposição de uma numa proposição da outra, mas somente as partes da proposição são traduzidas.
(E o dicionário não traduz apenas substantivos, mas ainda verbos, adjetivos, conectivos, etc.; e trata-os todos de modo igual.)
4.026 As denotações dos signos simples (das palavras) nos devem ser explicadas para que as compreendamos.
Com as proposições, no entanto, compreendemo-nos a nós mesmos.
4.027 Está na essência da proposição poder comunicar-nos um nôvo sentido.
4.03 Uma proposição deve comunicar nôvo sentido com velhas expressões.
A proposição nos comunica uma situação, de sorte que deve estar essencialmente vinculada a ela.
E a vinculação consiste precisamente em que ela é sua figuração lógica.
A proposição só asserta algo enquanto é figuração.
4.031 Uma situação é justaposta à proposição, por assim dizer, por tentativas.
É possível dizer diretamente: esta proposição representa esta ou aquela situação, em vez de esta proposição tem êste ou aquêle sentido.
4.0311 Um nome presenta uma coisa, outro, outra coisa, e estão ligados entre si de tal modo que o todo como quadro vivo — (ein lebendes Bild) — presenta o estado de coisas.
4.0312 A possibilidade da proposição se estriba no princípio da substituição dos objetos por meio de signos.
Meu pensamento basilar é que as "constantes lógicas" nada substituem; que a lógica dos fatos não se deixa substituir.
4.032 A proposição é uma figuração da situação únicamente enquanto fôr lògicamente articulada.
(Também a proposição Ambulo é composta, pois sua raiz com outra desinência nos dá outro sentido, o mesmo acontecendo se esta desinência estiver com outra raiz.)
4.04 Tanto se distinguirá na proposição quanto na situação que ela representa.
Ambos devem possuir a mesma multiplicidade lógica (matemática). (Cf. a mecânica de Hertz a propósito dos modelos dinâmicos.)
4.041 Esta multiplicidade matemática não pode naturalmente ser de nôvo afigurada. Ao afigurar não é possível colocar-se fora dela.
4.0411 Se quiséssemos, por exemplo, exprimir o que é expresso por "(x) . fx" apondo um índice junto a "fx", a saber: "Univ. fx", isto não bastaria — não saberíamos o que foi universalizado. Se quiséssemos indicá-lo por um índice "α" — tal como "f(xα)", isto também não bastaria — não conheceríamos o escopo da designação da universalidade.
Se quiséssemos tentar graças à introdução de uma marca no lugar do argumento — por exemplo: "(A, A) . F(A, A)" —, isto também não bastaria, pois não poderíamos fixar a identidade das variáveis. E assim por diante.
Todos êsses modos de designação não bastam, porquanto não possuem a necessária multiplicidade matemática.
4.0412 Pelo mesmo motivo não basta a explicação idealista da visão das relações espaciais por meio de "óculos espaciais", já que êstes não podem explicar a multiplicidade que essas relações possuem.
4.05 Compara-se a realidade com a proposição.
4.06 Somente por isso a proposição pode ser verdadeira ou falsa, quando ela é uma figuração da realidade.
4.061 Se não se observar que uma proposição possui sentido independente dos fatos, então fàcilmente se acredita que o verdadeiro e o falso são relações eqüiponderantes entre signos e designado.
Seria então possível dizer, por exemplo, que "p" designa segundo a modalidade do verdadeiro o que "∼p", segundo a modalidade do falso, etc.
4.062 Não seria possível fazer-se entender com proposições falsas assim como se fêz até agora com verdadeiras; desde que se soubesse que são mentadas falsamente? Não! Porquanto uma proposição é verdadeira se a situação é tal como dizemos por seu intermédio, e se com "p" mentássemos "∼p" e se a situação fosse tal como a mentamos, então "p" não seria falso na nova concepção mas verdadeiro.
4.063 É importante, porém, que os signos "p" e "∼p" possam dizer a mesma coisa, pois isto mostra que. o signo "∼" a nada corresponde na realidade.
A negação aparecer numa proposição não é marca característica de seu sentido (∼∼p = p).
As proposições "p" e "∼p" têm sentido oposto, mas a elas corresponde uma e a mesma realidade.
Afiguremo-nos um exemplo para esclarecer o conceito de verdade: dada uma mancha preta num papel branco; pode-se descrever a forma da mancha indicando para cada ponto dela se é branco ou prêto. Ao fato de que um ponto seja prêto corresponde um fato positivo; de que um ponto seja branco (não-prêto) corresponde um fato negativo. Se designo um ponto da superfície (um valor de verdade, segundo Frege), então isto corresponde à assunção estabelecida pelo julgamento, etc., etc.
Para poder dizer que um ponto é prêto ou branco antes devo saber quando lhe chamo de branco e quando de prêto — para poder dizer "p" é verdadeiro (ou falso) devo ter determinado em que condições chamo "p" verdadeiro e, dêsse modo, determino o sentido da proposição.
O símile falha apenas no ponto seguinte: podemos indicar um ponto do papel sem saber o que seja branco e o que seja prêto; uma proposição sem sentido, porém, não corresponde a nada, pois não designa coisa alguma (valor de verdade) cujas propriedades fôssem chamadas "falsas" ou "verdadeiras" — o verbo de uma proposição não é "é verdadeiro" ou "é falso", como acreditava Frege, mas o verbo já deve conter o que "é verdadeiro".
4.064 Cada proposição já deve possuir um sentido; a afirmação não lho pode dar pois afirma precisamente o sentido. E o mesmo vale para a negação, etc.
4.0641 É possível dizer: a negação já se reporta ao lugar lógico determinado pela proposição negada.
A proposição negadora determina outro lugar lógico do que a negada.
A proposição negadora determina um lugar lógico com a ajuda do lugar lógico da proposição negada, quando descreve aquêle permanecendo fora dêste.
Poder negar de novo a proposição negada mostra que o que é negado já é uma proposição, não sendo a mera preparação de uma proposição.
4.1 A proposição representa a subsistência e a não-subsistência dos estados de coisas.
4.11 A totalidade das proposições verdadeiras é tôda a ciência da natureza (ou a totalidade das ciências naturais).
4.111 A filosofia não é ciência da natureza.
(A palavra "filosofia" deve denotar alguma coisa que se coloca acima ou abaixo mas não ao lado das ciências naturais.)
4.112 A finalidade da filosofia é o esclarecimento lógico dos pensamentos.
A filosofia não é teoria mas atividade.
Uma obra filosófica consiste essencialmente em comentários.
A filosofia não resulta em "proposições filosóficas" mas em tornar claras as proposições.
A filosofia deve tomar os pensamentos que, por assim dizer, são vagos e obscuros e torná-los claros e bem delimitados.
4.1121 A psicologia não é mais aparentada à filosofia do que qualquer outra ciência natural.
A teoria do conhecimento é a filosofia da psicologia.
Não corresponde meu estudo sobre a linguagem simbólica ao estudo dos processos do pensamento, os quais os filósofos consideram tão essencial para a filosofia da lógica? Eles apenas se confundem na maior parte com investigações psicológicas inessenciais, existindo um perigo análogo para meu método.
4.1122 A teoria de Darwin não tem mais a ver com a filosofia do que qualquer outra hipótese das ciências naturais.
4.113 A filosofia delimita o domínio contestável das ciências naturais.
4.114 Deve delimitar o pensável e com isso o impensável.
Deve demarcar o impensável do interior por meio do pensável.
4.115 Denotará o indizível, representando claramente o dizível.
4.116 Tudo em geral o que pode ser pensado o pode claramente. Tudo que se deixa exprimir, deixase claramente.
4.12 A proposição pode representar a realidade inteira, não pode, porém, representar o que ela deve ter em comum com a realidade para poder representá-la — a forma lógica.
Para podermos representar a forma lógica seria preciso nos colocar, com a proposição, fora da lógica; a saber, fora do mundo.
4.121 A proposição não pode representar a forma lógica, esta espelha-se naquela.
Não é possível representar o que se espelha na linguagem.
O que se exprime na linguagem não podemos expressar por meio dela.
A proposição mostra a forma lógica da realidade.
Ela a exibe.
4.1211 Dêsse modo, a proposição "fa" mostra que o objeto a aparece em seu sentido, duas proposições "fa" e "ga" que em ambas se trata do mesmo objeto.
Se duas proposições se contradizem, isto é mostrado por sua estrutura; do mesmo modo, quando uma se segue da outra. E assim por diante.
4.1212 O que pode ser mostrado não pode ser dito.
4.1213 Agora compreendemos nosso sentimento de que estamos de posse de uma concepção lógica correta somente quando tudo esteja conforme em nossa linguagem simbólica.
4.122 Podemos em certo sentido falar de propriedades formais de objetos e estados de coisas, em particular de propriedades da estrutura dos fatos, e no mesmo sentido de relações formais e de relações de estruturas.
(Em lugar de propriedade da estrutura falo também de "propriedade interna", em lugar de relação de estruturas, "relação interna".
Introduzo essas expressões para mostrar o fundamento da confusão, muito difundida no meio dos filósofos, entre relações internas e relações propriamente ditas (externas).)
A subsistência de tais propriedades e de tais relações internas não pode ser, todavia, afirmada por proposições, mas se mostra nas proposições que apresentam os estados de coisas e os objetos em questão.
4.1221 A uma propriedade interna de um fato podemos ainda chamar de traço dêsse fato. (No sentido em que falamos, por exemplo, de traços faciais.)
4.123 Uma propriedade é interna quando fôr impensável que seu objeto não a possua.
(Esta côr azul e aquela estão na relação interna de mais claro e eo ipso mais escuro. É impensável êstes dois objetos não estarem nesta relação.)
(Ao emprego impreciso das palavras "propriedade" e "relação" corresponde aqui o emprêgo impreciso da palavra "objeto".)
4.124 A subsistência de uma propriedade interna de uma situação possível não se expressa por uma proposição mas, na proposição que a representa, por uma propriedade interna desta proposição.
Seria, pois, absurdo tanto imputar como não imputar à proposição uma propriedade formal.
4.1241 Não se podem distinguir as formas umas das outras dizendo que uma tem esta propriedade e aquela, outra, pois isto pressupõe que teria sentido assertar ambas propriedades de ambas as formas.
4.125 A subsistência de uma relação interna entre situações possíveis exprime-se lingüìsticamente por meio de uma relação interna entre as proposições que as representam.
4.1251 Isto liquida a disputa "se tôdas as relações são internas ou externas".
4.1252 Às séries ordenadas por relações internas chamo de séries formais.
A série dos números não se ordena segundo uma relação externa, mas segundo uma relação interna.
Da mesma maneira, a série de proposições "aRb",
"(∃x) : aRx . xRb",
"(∃x, y) : aRx . xRy . yRb", e assim por diante.
(Estando b numa dessas relações com a, chamo-lhe de sucessor de a.)
4.126 No mesmo sentido em que falamos de propriedades formais, podemos também nos referir a conceitos formais.
(Introduzo essa expressão com o intuito de deslindar a confusão dos conceitos formais com os conceitos autênticos, que perpassa tôda a velha lógica.)
Não é possível exprimir por uma proposição que algo caia sob um conceito formal como um objeto dêle. Isto se mostra, porém, no signo dêsse próprio objeto. (O nome mostra que designa um objeto, os signos numéricos, que designam um número, etc.)
Os conceitos formais não podem, pois, como os conceitos pròpriamente ditos, ser representados por uma função.
Porquanto suas marcas características, as propriedades formais, não se representam por funções. A expressão da propriedade formal é um traço de certos símbolos.
O signo das marcas características de um conceito formal é um traço próprio a todos os símbolos, cujas denotações caem sob o conceito.
A expressão do conceito formal é uma variável proposicional, em que apenas êste traço próprio é constante.
4.127 A variável proposicional designa o conceito formal, e seus valôres, os objetos que caem sob êsse conceito.
4.1271 Cada variável é signo de um conceito formal.
Porquanto cada variável representa uma forma constante que todos os seus valores possuem, e que pode ser concebida como a propriedade formal dêsses valôres.
4.1272 De sorte que a variável nome "x" é o signo apropriado ao pseudoconceito objeto.
Sempre que a palavra "objeto" ("coisa", etc.) fôr corretamente empregada, será expressa na ideografia pela variável nome.
Por exemplo, na proposição "Há dois objetos que...", por "(∃x, y)...".
Sempre, contudo, que fôr empregada de outra maneira, a saber, como palavra de um conceito propriamente dito, nascem pseudoproposições absurdas.
Não se pode dizer, por exemplo, "Há objetos" como se diz "Há livros". Nem tampouco "Há 100 objetos" ou "Há ℵ0 objetos".
E é absurdo falar do número de todos os objetos. O mesmo vale para as palavras "complexo", "fato", "função", "número", etc.
Tôdas designam conceitos formais e são representadas na ideografia por variáveis e não por funções ou classes. (Como Frege e Russell acreditavam.)
Expressões como "1 é um número", "Há apenas um zero" e todas as outras semelhantes são absurdas.
(É, pois, absurdo dizer "Há apenas um 1", tanto quanto seria absurdo dizer: 2 + 2 é às 3 horas igual a 4.)
4.12721 O conceito formal já está dado com um objeto que cai sob êle. Não se pode, portanto, introduzir como conceitos fundamentais objetos de um conceito formal e ainda o próprio conceito formal. Não se pode, por exemplo, introduzir o conceito de função e ainda funções especiais (como Russell) na qualidade de conceitos fundamentais; ou também o conceito de número e números determinados.
4.1273 Se quisermos exprimir, na ideografia, a proposição universal: "b é sucessor de a", precisamos de uma expressão para o termo geral da série formal: aRb ; (∃x) : aRx . xRb ; (∃x, y) : aRx . xRy . yRb, ... Só é possível exprimir o têrmo universal de uma série formal por meio de uma variável, pois o conceito: membro de uma série formal, é um conceito formal. (A isso desatentaram Frege e Russell; a maneira pela qual pretendem exprimir proposições universais, como a mencionada, é por isso falsa, contendo um circulus vitiosus.)
Podemos determinar o têrmo universal da série formal dando seu primeiro têrmo e a forma geral da operação que gera o termo seguinte a partir da proposição precedente.
4.1274 É absurda a pergunta pela existência de um conceito formal, pois não há proposição que possa respondê-la.
(Não é possível, por exemplo, perguntar: "Há proposições sujeito-predicado inanalisáveis?")
4.128 As formas lógicas são anuméricas.
De sorte que não há na lógica números excelentes, não havendo monismo ou dualismo filosófico, etc.
4.2 O sentido de uma proposição é sua concordância ou sua discordância com a possibilidade da subsistência ou não-subsistência de estados de coisas.
4.21 A proposição mais simples, a proposição elementar, afirma a subsistência de um estado de coisas.
4.211 É um signo da proposição elementar que nenhuma outra possa estar em contradição com ela.
4.22 A proposição elementar é constituída de nomes. É uma conexão, um encadeamento de nomes.
4.221 É óbvio que, graças à análise da proposição, devemos chegar a proposições elementares que consistam de nomes numa vinculação imediata.
Pergunta-se aqui como se dá o vínculo proposicional.
4.2211 Ainda que o mundo fôsse infinitamente complexo, de modo que cada fato fôsse constituído por muitos estados de coisas ao infinito e cada estado de coisas composto por muitos objetos ao infinito, mesmo assim deveria haver objetos e estados de coisas.
4.23 O nome só aparece na proposição em conexão com proposições elementares.
4.24 Os nomes são os símbolos mais simples, indico-os por letras singulares ("x", "y", "z").
Escrevo as proposições elementares como fun- ção dos nomes, com a seguinte forma: "fx", "ϕ(x, y)", etc.
Ou indico-as por meio das letras p, q, r.
4.241 Se emprego dois signos numa única e mesma denotação, isto vem expresso quando introduzo entre ambos o signo "=".
"a = b" equivale pois a: o signo "a" é substituível pelo signo "b".
(Se introduzo por meio de uma equação um novo signo "b", determinando que deve substituir um signo "a" já conhecido, então escrevo a equação — definição — (como Russell) na forma "a = b Def.". A definição é uma regra a propósito de signos.)
4.242 Expressões de forma "a = b" são, pois, recursos de representação; nada dizem a respeito da denotação dos signos "a", "b".
4.243 Podemos compreender dois nomes sem saber se designam a mesma coisa ou duas coisas diferentes? — Podemos compreender uma proposição em que dois nomes aparecem sem saber se denotam o mesmo ou o diverso?
Conhecendo a denotação de uma palavra inglêsa e de outra alemã de mesma denotação, não me é possível ignorar que ambas possuem a mesma denotação, não me é possível não traduzi-las uma pela outra.
Expressões como "a = a" ou destas derivadas não são nem proposições elementares nem signos significativos. (Isto será mostrado mais tarde.)
4.25 Se a proposição elementar fôr verdadeira, o estado de coisas subsiste; se fôr falsa, o estado de coisas não subsiste.
4.26 A indicação de tôdas as proposições elementares verdadeiras descreve o mundo completamente. O mundo é completamente descrito pela indicação de tôdas as proposições elementares mais a indicação de quais são as verdadeiras e quais as falsas.
4.27 A respeito da subsistência e da não-subsistência de n estados de coisas dá-se [math]\displaystyle{ K_n = \sum_{\nu=0}^n \binom{n}{\nu} }[/math] possibilidades.
É possível todas as combinações de estados de coisas subsistirem e outras não subsistirem.
4.28 A essas combinações correspondem assim muitas possibilidades de verdade — e falsidade — de n proposições elementares.
4.3 As possibilidades de verdade das proposições elementares denotam as possibilidades da subsistência e da não-subsistência de estados de coisas.
4.31 Podemos representar as possibilidades de verdade do seguinte modo ("V" denota "verdadeiro", "F" denota "falso". As séries de "V" e "F" sob a série das proposições elementares denotam suas possi- bilidades de verdade num simbolismo fàcilmente compreensível):
| p | q | r |
|---|---|---|
| V | V | V |
| F | V | V |
| V | F | V |
| V | V | F |
| F | F | V |
| F | V | F |
| V | F | F |
| F | F | F |
| p | q |
|---|---|
| V | V |
| F | V |
| V | F |
| F | F |
| p |
|---|
| V |
| F |
4.4 A proposição é a expressão da concordância e da discordância com as possibilidades de verdade das proposições elementares.
4.41 As possibilidades de verdade das proposições elementares são as condições da verdade e falsidade das proposições.
4.411 É de antemão provável que a introdução de proposições elementares seja fundamental para a compreensão de todos os outros modos de proposição. A compreensão das proposições universais, com efeito, depende palpàvelmente da das proposições elementares.
4.42 No que respeita à concordância ou à discordância de uma proposição com as possibilidades de verdade de n proposições elementares há [math]\displaystyle{ \sum_{\kappa=0}^{K_n} \binom{K_n}{\kappa} = L_n }[/math] possibilidades
4.43 A concordância com as possibilidades de verdade podemos exprimi-la apondo-lhe no esquema a insígnia "V" (verdadeiro).
A falta dessa insígnia denota a discordância.
4.431 A expressão da concordância e da discordância com as possibilidades de verdade das proposições elementares exprime as condições de verdade da proposição.
A proposição é expressão de suas condições de verdade.
(Por isso Frege agiu corretamente ao tomá-las desde logo como explicação dos signos de sua ideografia. Somente a explicação do conceito de verdade em Frege é falsa: fôssem realmente "o verdadeiro" e "o falso" os objetos e os argumentos em ∼p, etc., então, segundo a determinação de Frege, o sentido de "∼p" não estaria determinado de modo algum.)
4.44 O signo que surge por meio da aposição dessa insígnia "V" às possibilidades de verdade é um signo proposicional.
4.441 É claro que nenhum objeto (ou complexo de objetos) corresponde ao complexo de signos "F" ou "V"; tampouco como às linhas horizontais ou verticais ou aos parenteses. — Não há "objetos lógicos".
Algo análogo vale naturalmente para todos os signos que exprimem a mesma coisa que os esquemas de "V" e "F".
4.442 Por exemplo:
“
| p | q | |
|---|---|---|
| V | V | V |
| F | V | V |
| V | F | |
| F | F | V |
”
é um signo proposicional.
(O "traço de juízo" "⊢", introduzido por Frege, do ponto de vista lógico carece inteiramente de denotação; indica em Frege (e Russell) que tais autores tomam como verdadeiras as proposições assim designadas. "⊢" pertence tão pouco à construção da proposição como, por exemplo, a numeração das proposições. Uma proposição não pode, de forma alguma, assertar de si mesma que é verdadeira.)
Se as séries de possibilidades de verdade forem fixadas de vez no esquema, por meio de uma regra de combinação, a última coluna por si só já exprime as condições de verdade. Ao escrevermos esta coluna como série, o signo proposicional será o seguinte: "(VV–V) (p, q)", ou de modo mais nítido "(VVFV) (p, q)".
(O número de posições no interior dos parênteses da esquerda está determinado pelo número de têrmos dos da direita.)
4.45 Para n proposições elementares há Ln grupos possíveis de condições de verdade.
Os grupos de condições de verdade que pertencem às possibilidades de verdade de um número de proposições elementares ordenam-se numa série.
4.46 Entre os grupos possíveis de condições de verdade há dois casos extremos.
No primeiro caso a proposição é verdadeira para todas as condições de verdade das proposições elementares. Dizemos então que as condições de verdade são tautológicas.
No segundo caso a proposição é falsa para tôdas as condições de verdade: as condições de verdade são contraditórias.
No primeiro caso chamamos à proposição de tautologia, no segundo, contradição.
4.461 A proposição mostra o que diz, a tautologia e a contradição que não dizem nada.
A tautologia não possui condições de verdade pois é verdadeira sob qualquer condição; a contradição sob nenhuma condição é verdadeira.
A tautologia e a contradição são vazias de sentido.
(Como o ponto de onde duas flechas partem em direções opostas.)
(Nada sei, por exemplo, a respeito do tempo se sei que chove ou não chove.)
4.4611 A tautologia a contradição não são, porém, absurdas; pertencem ao simbolismo do mesmo modo que "0" pertence ao simbolismo da aritmética.
4.462 A tautologia e a contradição não são figurações da realidade. Não representam nenhuma situação possível, porquanto aquela permite tôdas as situações possíveis, esta, nenhuma.
4.463 Na tautologia as condições de concordância com o mundo — as relações representativas — cancelam-se umas às outras, pois não se põem em relação representativa com a realidade.
As condições de verdade determinam o campo aberto aos fatos pela proposição.
(A proposição, a figuração, o modêlo são, num sentido negativo, como um corpo sólido que limita a liberdade de movimento de outro; no sentido positivo, como um espaço limitado por uma substância sólida onde um corpo pode ter lugar.)
A tautologia deixa inteiramente à realidade o espaço lógico — infinito —; a contradição preenche o espaço lógico inteiro, não deixando à realidade ponto algum. Nenhuma delas pode, por conseguinte, determinar a realidade de um modo qualquer.
4.464 É certa a verdade da tautologia, da proposição é possível e da contradição impossível.
(Certo, possível, impossível: temos aqui a indicação da gradação que precisamos para a teoria da probabilidade.)
4.465 O produto lógico de uma tautologia e de uma proposição diz o mesmo que a proposição. O produto é, pois, idêntico à proposição, porquanto não se pode alterar o essencial do símbolo sem alterar seu sentido.
4.466 A uma determinada união lógica de signos corresponde uma determinada união da denotação dêles; cada união arbitrária corresponde apenas a signos desunidos.
Isto quer dizer que proposições, verdadeiras para qualquer situação, não podem ser em geral uniões de signos, pois, caso contrário, apenas determinadas uniões de objetos poderiam corresponder.
(E a nenhuma união lógica corresponde nenhuma união de objetos.)
Tautologia e contradição são casos-limites da união de signos, a saber, sua dissolução.
4.4661 Por certo na tautologia e na contradição os signos ainda estão ligados uns aos outros, isto é, relacionam-se entre si, mas estas relações são desprovidas de denotação, são inessenciais para o símbolo.
4.5 Agora parece possível estabelecer a forma mais geral da proposição, isto é, estabelecer uma descri- ção das proposições numa linguagem simbólica qualquer, de tal modo que cada um dos sentidos possíveis poderia ser expresso por um símbolo adequado à descrição e cada símbolo adequado à descrição poderia exprimir um sentido, se as denotações dos nomes fôssem convenientemente escolhidas.
É claro que, descrevendo a forma mais geral de uma proposição, somente o que é essencial deve ser descrito — caso contrário não seria a mais geral.
Prova-se a existência de uma forma geral da proposição porque não deve haver proposição alguma cuja forma não seja antes pressuposta (isto é, construída). A forma geral da proposição é: isto está do seguinte modo.
4.51 Supondo que tôdas as proposições elementares me sejam dadas, surge a pergunta: quais são as proposições que posso formar a partir delas? E estas são tôdas as proposições e assim elas são limitadas.
4.52 As proposições são tudo o que se segue da totalidade das proposições elementares (sem dúvida por que se parte da totalidade de todas elas). (Num certo sentido é possível dizer que tôdas as proposições são generalizações das proposições elementares.)
4.53 A forma geral da proposição é uma variável.
5 A proposição é uma função de verdade das proposições elementares.
(A proposição elementar é uma função de verdade de si mesma.)
5.01 As proposições elementares são os argumentos de verdade da proposição.
5.02 E fácil confundir argumentos de uma função com índices de nomes. Conheço em particular a denotação de um signo que a contém tanto pelo argumento como pelo índice.
No sinal de Russell "+c", por exemplo, "c" é um índice que indica valer o signo inteiro para a soma de números cardinais. Esta designação, porém, se apóia num ajuste arbitrário, de sorte que seria possível em vez de "+c" escolher outro signo simples; em "∼p", entretanto, "p" não é índice algum, mas argumento: o sentido de "∼p" não pode ser compreendido sem que antes o sentido de "p" o seja. (No nome Julius Caesar, "Julius" é índice. Este é sempre parte da descrição do objeto cujos nomes vinculamos a êle. Por exemplo, o Caesar da gente juliana.)
A confusão entre argumento e índice constitui, se não me engano, a base da teoria de Frege a respeito da denotação das proposições e das funções. Para Frege, as proposições da lógica seriam nomes, e seus argumentos, os índices dêsses nomes.
5.1 As funções de verdade se ordenam em séries.
Este é o fundamento da teoria da probabilidade.
5.101 As funções de verdade de todos os números de proposições elementares inscrevem-se no seguinte esquema:
| (VVVV)(p, q) | Tautologia | (Se p, então p; e se g, então q.) (p ⊃ p . q ⊃ q) |
| (FVVV)(p, q) | em palavras: | Não ambos p e q. (∼(p . q)) |
| (VFVV)(p, q) | em palavras: | Se q, então p. (q ⊃ p) |
| (VVFV)(p, q) | em palavras: | Se p, então q. (p ⊃ q) |
| (VVVF)(p, q) | em palavras: | p ou q (p ∨ q) |
| (FFVV)(p, q) | em palavras: | Não q. ∼q |
| (FVFV)(p, q) | em palavras: | Não p. ∼p |
| (FVVF)(p, q) | em palavras: | p ou q mas não ambos. (p . ∼q : ∨ : q . ∼p) |
| (VFFV)(p, q) | em palavras: | Se p, então q; e se q, então p. (p ≡ q) |
| (VFVF)(p, q) | em palavras: | p |
| (VVFF)(p, q) | em palavras: | q |
| (FFFV)(p, q) | em palavras: | Nem p nem q. (∼p . ∼q) ou (p | q) |
| (FFVF)(p, q) | em palavras: | p e não q. (p . ∼q) |
| (FVFF)(p, q) | em palavras: | q e não p. (q . ∼p) |
| (VFFF)(p, q) | em palavras: | q e p (q . p) |
| (FFFF)(p, q) | Contradição | (p e não p; e q e não g.) (p . ∼p . q . ∼q) |
A essas possibilidades de verdade de seus argumentos de verdade, que confirmam as proposições, chamo de seus fundamentos de verdade.
Se os fundamentos de verdade comuns a um número de proposições, também forem fundamentos de verdade de uma proposição determinada, dizemos então que a verdade dessa proposição se segue da verdade daquelas outras.
Em particular a verdade de uma proposição "p" segue-se da de outra "q" se todos os fundamentos de verdade da segunda forem fundamentos de verdade da primeira.
Os fundamentos de verdade de uma estão contidos nos da outra; assim, p segue-se de q.
Se p segue-se de q, o sentido de "p" está contigo no sentido de "q".
5.123 Se um deus criasse um mundo em que certas proposições fôssem verdadeiras, criaria do mesmo modo um mundo com o qual concordariam tôdas suas proposições conseqüentes. E assim similarmente não poderia criar um mundo em que a proposição "p" fôsse verdadeira, sem criar todos os objetos dela.
5.124 A proposição afirma cada proposição que dela se segue.
5.1241 "p . q" é uma das proposições que afirmam "p" e ao mesmo tempo uma das proposições que afirmam "q".
Duas proposições são opostas uma à outra se não existir qualquer proposição significativa que afirme ambas.
Cada proposição que contradiz a outra, nega-a.
5.13 Que a verdade de uma proposição segue-se da verdade de outras vemos a partir da estrutura das proposições.
5.131 Se a verdade de uma proposição segue-se da verdade de outras, isto se exprime nas relações que as formas dessas proposições mantêm entre si; e não precisamos com efeito colocá-las primeiro naquelas relações, unindo-as com outra proposição, porquanto essas relações são internas e subsistem enquanto aquelas proposições subsistirem, e porque elas subsistem.
5.1311 Se pois de p ∨ q e de ~p inferimos q, a relação entre as formas das proposições "p ∨ q" e "∼p" se oculta em virtude da maneira de simbolizar. Se em lugar de "p ∨ q", escrevemos, por exemplo, "p | q . | . p | q" e em lugar de "∼p" "p | p" (p | q = nem p nem q), logo se torna clara a conexão interna.
De (x).fx pode-se inferir fa; isto mostra que a universalidade já está presente no símbolo "(x).fx".
5.132 Se p segue-se de q, posso então inferir de q, p; deduzir p de q.
O modo de inferência há de ser captado apenas de ambas as proposições.
Somente elas podem justificar a inferência.
"Regras de inferência" que — como em Frege e Russell — devem justificar a inferência são vazias de sentido e seriam supérfluas.
5.133 Tôda dedução se dá a priori.
5.134 De uma proposição elementar nenhuma outra pode ser deduzida.
5.135 De modo algum é possível inferir da subsistência de uma situação qualquer a subsistência de uma situação inteiramente diferente dela.
5.136 Não há nexo causal que justifique tal inferência.
5.1361 Não podemos inferir os acontecimentos do futuro a partir daqueles do presente.
É superstição a crença no nexo causal.
5.1362 A liberdade da vontade consiste em não poder conhecer agora as ações futuras. Só poderíamos conhecê-las se a causalidade fôsse uma necessidade interna, como a inferência lógica. A conexão entre o conhecer e o conhecido é a mesma da necessidade lógica.
("A sabe que p ocorre" é vazia de sentido se p fôr uma tautologia.)
5.1363 Sendo uma proposição óbvia para nós, não se segue que seja verdadeira; por conseguinte, a obviedade não é justificativa para nossa crença em sua verdade.
5.14 Se uma proposição segue-se de outra, esta diz mais do que aquela, aquela menos do que esta. Se p segue-se de q e q de p, ambas são pois uma única e mesma proposição.
5.142 A tautologia segue-se de todas as proposições: não diz nada.
5.143 A contradição é algo comum às proposições e que nenhuma proposição tem em comum com outra. A tautologia é o que é comum a tôdas as proposições que não têm nada em comum entre si.
A contradição desaparece, por assim dizer, por fora, a tautologia, por dentro de todas as proposições.
A contradição é limite externo das proposições, a tautologia, seu centro dessubstancializado.
5.15 Seja Vr o número dos fundamentos de verdade da proposição "r", Vrs o número daqueles fundamentos de verdade da proposição "s" que ao mesmo tempo são fundamentos de verdade de "r"; chamamos então à relação: Vrs : Vr de medida de probabilidade que a proposição "r" tem em relação à proposição "s".
5.151 Seja num esquema como o de cima, no número 5.101, Vr o número de "V" da proposição r; Vrs o número daqueles "V" na proposição s que estão na mesma coluna com os "V" da proposição r. A proposição r tem em relação à proposição s a probabilidade Vrs : Vr.
5.1511 Não há nenhum objeto particular próprio às proposições probabilísticas.
5.152 Chamamos mútuamente independentes as proposições que não têm em comum com outras qualquer argumento de verdade.
Duas proposições elementares têm entre si a probabilidade ½.
Se p segue-se de q, a proposição "q" tem em relação à proposição "p" a probabilidade 1. A certeza da inferência lógica é o caso-limite da probabilidade.
(Aplicação à tautologia e à contradição.)
5.153 Uma proposição não é nem provável nem improvável. Um acontecimento se dá ou não se dá, não há meio-têrmo.
5.154 Suponhamos que numa urna estejam tantas bolas brancas quantas pretas (e nenhuma a mais). Tiro uma bola depois da outra e as reponho de novo na urna. Posso, então, estabelecer pela experiência que o número das bolas pretas tiradas e o das bolas brancas tiradas se aproximam progressivamente um do outro.
Isto não é, portanto, um fato matemático.
Se disser agora: é igualmente provável que tirarei uma bola branca como uma preta, isso quer dizer: tôdas as circunstâncias que me são conhecidas (incluindo as leis da natureza tomadas hipotèticamente) não conferem a um acontecimento nenhuma probabilidade a mais do que a outro. A saber, estão — como se compreende fàcilmente a partir das explicações acima — numa relação de probabilidade de ½.
O que verifiquei pela experiência é que ambos os acontecimentos independem das circunstâncias das quais não tenho conhecimento mais próximo.
5.155 A unidade das proposições probabilísticas é a seguinte: as circunstâncias — de que, aliás, não tenho conhecimento mais amplo — conferem a um determinado acontecimento tal e tal grau de probabilidade.
5.156 Dêsse modo, a probabilidade é uma generalização.
Envolve uma descrição geral de uma forma proposicional.
Só na falta de certeza precisamos de probabilidade. — Quando não conhecemos um fato completamente, mas ao menos sabemos algo a respeito de sua forma.
(Uma proposição pode, com efeito, ser uma figuração incompleta de uma certa situação, entretanto sempre é uma figuração completa.)
A proposição probabilística é como se fôsse um extrato de outras proposições.
5.2 As estruturas das proposições mantêm entre si relações internas.
5.21 Podemos trazer essas relações internas para nosso modo de expressão, representando uma proposição como resultado de uma operação que a produz de outras proposições (as bases da operação).
5.22 A operação é a expressão de uma relação entre as estruturas do resultado e de suas bases.
5.23 Operação é o que deve acontecer com uma proposição a fim de gerar outra a partir dela.
5.231 E isso naturalmente dependerá de suas propriedades formais, da semelhança interna de suas formas.
5.232 A relação interna que ordena uma série equivale à operação que produz um têrmo a partir de outro.
5.233 A operação só pode ter lugar pela primeira vez onde uma proposição nasce de outra de modo lògicamente denotativo; onde começa, portanto, a construção lógica da proposição.
5.234 As funções de verdade das proposições elementares resultam de operações que têm como bases as proposições elementares. (A essa operação chamo de operação-verdade.)
5.2341 O sentido de uma função de verdade de p é função do sentido de p.
Negação, soma lógica, multiplicação lógica, etc., etc., são operações.
(A negação inverte o sentido da proposição.)
5.24 A operação mostra-se numa variável; mostra como de uma forma de proposições se pode chegar a outra.
Torna expressa a diferença de formas.
(E o que é comum às bases e ao resultado da operação são precisamente essas bases.)
5.241 A operação não designa forma alguma, mas apenas a diferença de formas.
5.242 A mesma operação que produz "q" de "p", produz também de "q", "r" e assim por diante. Isto só pode ser expresso porque "p", "q", "r", etc., são variáveis que tornam expressas de um modo geral certas relações formais.
5.25 A realização de uma operação não caracteriza o sentido de uma proposição.
A operação nada asserta além de seu resultado e isto depende das bases dessa operação.
(Operações e funções não devem ser confundidas.)
5.251 Uma função não pode ser seu próprio argumento; no entanto, o resultado de uma operação pode muito bem ser sua própria base.
5.252 Sòmente assim é possível o progresso de um têrmo a outro na série formal (de tipo a tipo na hierarquia de Russell e Whitehead). (Russell e Whitehead não admitiram a possibilidade dêsse progresso mas fizeram dêle uso repetido.)
5.2521 À aplicação progressiva de uma operação sôbre seu próprio resultado chamo sua aplicação sucessiva. ("O'O'O'a" resulta de três aplicações sucessivas de "O'ξ" sobre "a").
Em sentido semelhante falo da aplicação sucessiva de muitas operações sobre um número de proposições.
5.2522 O têrmo geral de uma seqüência formal a, O'a, O'O'a, ... escrevo por isso do seguinte modo: "[a, x, O'x]". Esta expressão entre colchêtes é uma variável. O primeiro têrmo da expressão do colchête é o início da série formal, o segundo a forma de um têrmo qualquer x da série e o terceiro a forma daquele têrmo da série que segue imediatamente a x.
5.2523 O conceito de aplicação sucessiva de operação equivale ao conceito "e assim por diante".
5.253 Uma operação pode anular o efeito de outra. Operações podem suprimir-se mùtuamente.
5.254 A operação pode desaparecer (por exemplo, a negação em "∼∼p", ~~p = p).
5.3 Todas as proposições resultam de operações- verdades sobre as proposições elementares.
A operação-verdade é o modo pelo qual a função de verdade nasce das proposições elementares.
Do mesmo modo que das proposições elementares nasce sua função de verdade, das funções de verdade nasce uma nova, de acordo com a essência da operação-verdade. Cada operação-verdade reproduz a partir de funções de verdade de proposições elementares uma função de verdade de proposições elementares, a saber, uma proposição. O resultado de cada operação-verdade realizada com resultados de operações-verdades sobre proposições elementares é de novo o resultado de uma operação-verdade sôbre proposições elementares.
Tôda proposição resulta de operações-verdades sôbre proposições elementares.
5.31 Os esquemas do n.° 4.31 possuem também denotação quando "p", "q", "r", etc., não são proposições elementares.
É fácil verificar que o signo proposicional no n.° 4.2 exprime uma função de verdade de proposições elementares ainda quando "p" e "q" são funções de verdade de proposições elementares.
5.32 Tôdas as funções de verdade resultam da aplicação sucessiva de um número finito de operações- verdades sobre proposições elementares.
5.4 Aqui se evidencia que não há "objetos lógicos", "constantes lógicas" (no sentido de Frege e Russell).
5.41 Porquanto: todos os resultados de operações-verdades sobre funções de verdade são idênticos, são uma e a mesma função de verdade de proposições elementares.
5.42 É óbvio que ∨, ⊃, etc., não são relações no sentido de direita e esquerda.
A possibilidade de definição cruzada dos "signos primitivos" de Frege e Russell já mostra que não são primitivos e que não designam relação alguma.
É evidente que "⊃", que definimos por "∼" e "v", é idêntico ao que serve para definir "∨" com a ajuda de "∼" e que éste "∨" é idêntico ao primeiro. E assim por diante.
5.43 Que de um fato p outros ao infinito seguir-se-ão, nomeadamente ∼∼p . ∼∼∼∼p, etc., é difícil, no início, de se acreditar. E não é menos extraordinário o número infinito de proposições da lógica (da matemática) seguir-se de meia dúzia de "princípios".
Tôdas as proposições da lógica dizem, porém, o mesmo; a saber, nada.
5.44 As funções de verdade não são funções materiais.
Já que, por exemplo, é possível gerar uma afirmação por meio da dupla negação, estará a negação — seja qual fôr o sentido — incluída na afirmação? "∼∼p" nega ∼p ou afirma ∼p, ou ambos?
A proposição "∼∼p" não trata a negação como um objeto; a possibilidade da negação, entretanto, já está antecipada na afirmação.
E se houvesse um objeto chamado "∼", então "∼∼p" deveria dizer outra coisa do que "p". Porquanto uma proposição trataria de "∼", enquanto a outra não.
5.441 Este desaparecimento das aparentes constantes lógicas se dá se "∼(∃x) . ∼fx" diz a mesma coisa que "(x). fx" ou "(∃x). fx . x = a", o mesmo que "fa".
5.442 Caso uma proposição nos seja dada, com ela dão-se os resultados de todas as operações-verdades que a têm como base.
5.45 Se houvesse signos lógicos primitivos, uma lógica correta deveria esclarecer suas posições, relativas umas às outras, e justificar sua existência. Deve tornar-se clara a construção da lógica a partir de seus signos primitivos.
5.451 Se a lógica possuísse conceitos básicos, êstes deveriam ser independentes uns dos outros. Admitido um conceito básico, deveria êle ser admitido em tôdas as vinculações em que em geral aparece. Não é possível, portanto, primeiramente admiti-lo numa conexão para em seguida admiti-lo em outra. Por exemplo, admitida a negação, devemos entendê-la tanto nas proposições de forma "∼p", como nas proposições tais que "∼(p ∨ q)", "(∃x) . ∼fx", etc. Não podemos introduzi-la primeiro para uma classe de casos, em seguida para outra: permaneceria duvidoso se sua denotação seria a mesma em ambos os casos, não havendo motivo de utilizar para êsses casos o mesmo modo de vincular os signos.
(Em resumo, para a introdução de signos primitivos vale, mutatis mutandis, o que Frege (nos Princípios da Aritmética) disse a propósito da introdução de signos por meio de definições.)
5.452 A introdução de um novo recurso no simbolismo da lógica sempre há de ser um acontecimento pleno de conseqüências. Nenhum recurso novo há de ser introduzido na lógica — entre parênteses ou à margem — por assim dizer, com cara inocente.
(Aparecem nos Principia Mathematica de Russell e Whitehead definições e princípios em palavras. Por que de repente palavras? Isto demanda uma justificação, que falta e deve faltar, pois o procedimento não é de fato permitido.)
Se todavia a introdução de novo recurso se provou necessária, deve-se perguntar imediatamente: onde êsse recurso deve ser sempre empregado? Sua localização na lógica deve ser esclarecida.
5.453 Todos os números da lógica devem deixar-se justificar.
Ou melhor, deve evidenciar-se que não há números na lógica.
Não há número excelente.
5.454 Não há na lógica um lado a lado, pois não há classificação.
Não pode haver na lógica o mais geral ou o mais especial.
5.4541 A solução dos problemas lógicos deve ser simples, já que êstes colocam o padrão da simplicidade.
Os homens sempre tiveram o pressentimento que deveria haver um domínio de questões cujas respostas — a priori — fôssem simétricas e unidas a uma construção acabada e regular.
Um domínio em que vale a sentença: simplex sigillum veri.
5.46 Caso se introduzam corretamente os signos lógicos, então já se introduz o sentido de todas as suas combinações; portanto, não apenas "p ∨ q" mas também "∼(p ∨ ∼q)", etc., etc. Já se teria introduzido, pois, o efeito de todas as combinações meramente- possíveis de parenteses. E assim estaria claro que os signos primitivos pròpriamente universais não seriam "p ∨ q", "(∃x) . fx" mas a forma mais geral de suas combinações.
5.461 Muito denota o fato aparentemente desimportante de que as pseudo-relações lógicas como ∨ ou ⊃ precisem de parenteses — ao contrário das relações reais.
A utilização de parenteses junto a esses pseudo-signos primitivos já indica que não são signos primitivos reais. E ninguém acreditará porventura que os parenteses possuam denotação autônoma.
5.4611 Os signos das operações lógicas são pontuações.
5.47 É claro que tudo o que se diz de antemão sobre a forma de todas as proposições deve ser dito ao menos uma vez.
Na proposição elementar já estão contidas tôdas as operações lógicas. Porquanto "fa" diz o mesmo que "(∃x) . fx . x = a".
Onde há composição já há argumento e função, e onde estão êstes já estão tôdas as constantes lógicas. Poder-se-ia dizer: uma constante lógica é aquilo que tôdas as proposições, conforme sua natureza, possuem em comum.
Isto é, porém, a forma proposicional geral.
5.471 A forma proposicional geral é a essência da proposição.
5.4711 Dar a essência da proposição quer dizer dar a essência de tôdas as descrições e, por conseguinte, a essência do mundo.
5.472 A descrição da forma proposicional mais geral é a descrição de um e um só signo primitivo universal da lógica.
5.473 A lógica deve cuidar de si mesma.
Um signo possível também deve poder designar. Tudo o que na lógica é possível também é permitido. ("Sócrates é idêntico" não diz nada, pois não há propriedade que se chame "idêntico". A proposição é absurda porque não encontramos uma determinação arbitrária, e não porque o símbolo em si e para si não fôsse permitido.)
Em certo sentido, não podemos errar na lógica.
5.4731 O óbvio de que Russell tanto fala só pode tornar-se prescindível porque a própria linguagem impede os erros lógicos. — Que a lógica seja a priori consiste em que nada ilógico pode ser pensado.
5.4732 Não podemos dar a um signo um sentido incorreto.
5.47321 O lema de Occam não é por certo uma regra arbitrária, ou que se justifique por seus resultados práticos; diz apenas que unidades de signos desnecessárias nada designam.
Signos que preenchem uma finalidade são lògicamente equivalentes, os que preenchem nenhuma são lògicamente desprovidos de denotação.
5.4733 Frege diz: cada proposição formada legitimamente deve ter um sentido; eu digo: cada proposição possível é legitimamente formada e, se não tiver sentido, isto só é possível porque não emprestamos denotação a algumas de suas partes constituintes.
(Ainda que acreditemos tê-lo feito.)
Dêsse modo, "Sócrates é idêntico" não diz nada, porque não emprestamos à palavra "idêntico" como adjetivo denotação alguma. Quando aparece como signo de igualdade, ela simboliza de maneira totalmente diversa — é outra a relação designadora —, de sorte que o símbolo, em ambos os casos, é inteiramente diferente; ambos os símbolos apenas têm, por acidente, o signo em comum.
5.474 O número das operações básicas necessárias depende apenas de nossa notação.
5.475 Trata-se apenas de formar um sistema de signos com número determinado de dimensões — com uma multiplicidade matemática determinada.
5.476 É claro que não se discute aqui o número de conceitos fundamentais que devem ser designados, mas a expressão de uma regra.
5.5 Cada função de verdade resulta da aplicação sucessiva da operação (– – – – –V)(ξ, . . . .) sôbre proposições elementares.
Esta operação nega tôdas as proposições no interior dos parênteses da direita, e a chamo negação dessas proposições.
5.501 Uma expressão nos parênteses cujos têrmos sejam proposições — quando é indiferente a seqüência dos têrmos nos parênteses — indico por meio de um signo da forma "[math]\displaystyle{ (\bar{\xi}) }[/math]". "ξ" é uma variável cujos valôres são os termos da expressão entre parênteses, e o traço sôbre a variável indica que esta substitui nos parênteses todos os seus valôres.
(Se, por exemplo, ξ tem 3 valôres P, Q, R, [math]\displaystyle{ (\bar{\xi}) }[/math] = (P, Q, R).)
Serão fixados os valores das variáveis.
A fixação é a descrição das proposições que a variável substitui.
É inessencial como se dá a descrição dos têrmos da expressão entre parênteses.
Podemos distinguir três maneiras de descrever: 1) Enumeração direta; neste caso podemos, em lugar das variáveis, colocar simplesmente seus valôres constantes. 2) Indicação de uma função fx cujos valôres, para todos os valores de x, constituam as proposições a serem descritas. 3) Indicação de uma lei formal segundo a qual cada proposição é formada; neste caso os termos da expressão entre parênteses são todos os termos de uma série formal.
5.502 Escrevo pois "[math]\displaystyle{ N (\bar{\xi}) }[/math]" em lugar de "(– – – – –V)(ξ, . . . .)".
[math]\displaystyle{ N (\bar{\xi}) }[/math] é a negação de todos os valores da variável proposicional ξ.
5.503 Evidentemente é fácil exprimir como proposições podem formar-se graças a esta operação e como proposições não têm de ser formadas graças a ela; e isto também pode encontrar uma expressão exata.
5.51 Se ξ tiver apenas um valor, [math]\displaystyle{ N (\bar{\xi}) }[/math] = ∼p (não p), se tiver dois valôres, [math]\displaystyle{ N (\bar{\xi}) }[/math] = ∼p . ∼q (nem p nem q).
5.511 Como é possível a lógica, que tudo abrange e espelha o mundo, precisar de tais artifícios e manipulações especiais? Somente porque tudo isto está ligado a uma rêde infinitamente fina, ao grande espelho.
5.512 "∼p" é verdadeiro se "p" fôr falso. Portanto, numa proposição verdadeira "~p", "p" é uma falsa proposição. Como lhe é possível fazer o traço "∼" concordar com a realidade?
O que é negado em "p" não é "∼", mas o que é comum a todos os signos dessa notação que negam p.
Dêsse modo, a regra comum pela qual se formam "∼p", "∼∼∼p", "∼p ∨ ∼p", "∼p . ∼p", etc., etc. (ao infinito). E o que é comum espelha a negação.
5.513 Poder-se-ia dizer: O que é comum a todos os símbolos que afirmam tanto p como q é a proposição "p . q". O que é comum a todos os símbolos que afirmam p ou q, é a proposição "p ∨ q".
E assim se pode dizer: Duas proposições são opostas mùtuamente se nada possuem em comum; e: cada proposição tem apenas um negativo, pois há apenas uma proposição que se situa inteiramente fora dela.
E na própria notação de Russell é evidente que "q : p ∨ ∼p" diz a mesma coisa que "q" e que "p ∨ ∼p" não diz nada.
5.514 Fixada uma notação, há nela uma regra pela qual são formadas todas as proposições negadoras de p, uma regra pela qual são formadas todas as proposições afirmadoras de p, uma regra pela qual são formadas todas as proposições afirmadoras de p ou q, e assim por diante. Essas regras são equivalentes aos símbolos e nelas espelha-se o seu sentido.
5.515 É preciso indicar que, em nossos símbolos, o que é ligado mùtuamente por "∨", ".", etc., deve ser proposições.
E isto ocorre, pois o símbolo "p" e "q" já pressupõem "∨", "∼", etc. Se o signo "p" em "p ∨ q" não substituir um signo complexo, não pode possuir sentido sozinho; mas então também os signos "p ∨ p", "p . p", que têm o mesmo sentido que "p", não teriam sentido. Se entretanto "p ∨ p" não tiver sentido, então do mesmo modo "p ∨ q" não terá sentido.
5.5151 Deve o signo da proposição negativa ser formado por meio do signo da positiva? Por que não se poderia exprimir a proposição negativa por um fato negativo? (Do seguinte modo: se "a" não se relacionar de modo determinado com "b", isto poderia exprimir que aRb não ocorre.)
Mas também aqui a proposição negativa se forma indiretamente pela positiva.
A proposição positiva deve pressupor a existência da proposição negativa e vice-versa.
5.52 Sejam os valores de ξ todos os valores de uma função fx para todos os valores de x, então [math]\displaystyle{ N (\bar{\xi}) }[/math] = ∼(∃x) . fx.
5.521 Separo o conceito todo das funções de verdade.
Frege e Russell introduziram a universalidade em ligação com o produto lógico ou a soma lógica e, dêsse modo, tornou-se difícil entender as proposições "(∃x) . fx" e "(x) . fx", em que ambas as idéias permanecem ocultas.
5.522 É peculiar à designação da universalidade: 1) referir-se a uma protofiguração lógica; 2) salientar as constantes.
5.523 A designação da universalidade aparece como argumento.
5.524 Caso os objetos estejam dados, nos estarão dados todos os objetos.
Caso as proposições elementares estejam dadas, já nos estão dadas todas as proposições elementares.
5.525 É incorreto interpretar a proposição "(∃x) . fx" — como Russell o faz — pelas palavras: "fx é possível".
Certeza, possibilidade e impossibilidade de uma situação não se expressam por meio de uma proposição mas por ser a expressão uma tautologia, uma proposição significativa ou uma contradição.
Aquêle caso precedente a que sempre se há de apelar já deve estar no próprio símbolo.
5.526 É possível descrever o mundo completamente por meio de proposições perfeitamente universalizadas, a saber, sem que de antemão um nome fôsse coordenado a um objeto.
Para chegar-se ao modo de expressão habitual deve-se simplesmente, depois de uma expressão "há um e um único x tal que...", dizer: e êste x é a.
5.5261 Uma proposição perfeitamente universalizada é, como qualquer outra proposição, composta. (Isto se mostra quando, em "(∃x, ϕ) . ϕx" devemos mencionar separadamente "ϕ" e "x". Ambos se correlacionam independentemente com o mundo, como na proposição que não foi universalizada.)
Característica de um símbolo composto: tem algo em comum com outro símbolo.
5.5262 A verdade ou a falsidade de cada proposição altera em algo a construção geral do mundo. E o campo que se deixa para sua construção por meio da totalidade das proposições elementares é precisamente aquêle que as proposições inteiramente universalizadas delimitam.
(Se uma proposição elementar fôr verdadeira, sempre haverá por isso mais uma proposição elementar verdadeira.)
5.53 Exprimo a igualdade de objetos pela igualdade de signos e não graças ao auxílio de um signo de igualdade. E a diversidade dos objetos por meio da diversidade de signos.
5.5301 É óbvio que a identidade não é uma relação entre objetos. Isto se torna muito claro quando se considera, por exemplo, a proposição "(x) : fx . ⊃ . x = a". A proposição diz meramente que apenas a satisfaz a função f, mas não diz que somente as coisas que mantêm uma certa relação com a satisfazem a função f.
Poder-se-ia sem dúvida dizer que sòmente a mantém esta relação com a, mas para exprimi-lo precisamos do signo da igualdade.
5.5302 A definição dada por Russell de "=" não é suficiente, pois, segundo ela, não é possível dizer que dois objetos possuem em comum tôdas as propriedades. (Ainda que esta proposição não seja correta, possui sentido.)
5.5303 Falando grosso modo: dizer de dois objetos que são idênticos é absurdo, e de um único que é idêntico consigo mesmo por certo não diz nada.
5.531 Não escrevo pois "f(a, b) . a = b" mas "f(a, a) (ou "f(b, b)"). Não escrevo "f(a, b)". ∼a = b", mas "f(a, b)".
5.532 E anàlogamente: não "(∃x, y) . f(x, y) . x = y", mas "(∃x). f(x, x)"; não "(∃x, y). f(x, y) . ∼x = y", mas "(∃x, y). f(x, y)".
(Desse modo, em vez da fórmula de Russell "(∃x, y) . f(x, y)", temos "(∃x, y). f(x, y) . ∨ . (∃x) . f(x, x)").
5.5321 Em vez de "(x) : fx ⊃ x = a" escrevemos, por exemplo, "(∃x). fx . ⊃ . fa : ∼(∃x, y). fx . fy".
E a proposição "sòmente um x satisfaz f( )" será "(∃x) . fx : ∼(∃x, y) . fx . fy".
5.533 O signo da igualdade não é, pois, parte essencial da ideografia.
5.534 Vemos então que pseudoproposições como: "a = a", "a = b . b = c . ⊃ a = c", "(x) . x = x", "(∃x) . x = a", etc., não se deixam inscrever de modo algum numa ideografia correta.
5.535 Desaparecem assim todos os problemas ligados a tais pseudoproposições.
Todos os problemas que encerra o axiom of infinity de Russell aqui se resolvem.
O axiom of infinity quer dizer, em têrmos da linguagem, que existem infinitamente muitos nomes com denotação diferente.
5.5351 Existem certos casos em que se é tentado a usar expressões da forma: "a = a", ou "p ⊃ p" e outras. E isto com efeito acontece quando se deve falar da protofiguração: proposição, coisa, etc. Russell, nos Principles of Mathematics transpôs o absurdo "p é uma proposição" no símbolo "p ⊃ p", tomando-o como hipótese diante de certas proposições a fim de que os lugares dos argumentos destas só pudessem ser ocupados por proposições.
(Já é um absurdo colocar diante de uma proposição a hipótese p ⊃ p para assegurar aos argumentos forma correta, porque a hipótese estabelecida para uma não-proposição enquanto argumento não se torna falsa mas absurda; além do mais, a própria proposição se torna absurda para argumentos de gênero incorreto, de sorte que se conserva tanto boa como má diante dos argumentos incorretos, assim como a hipótese sem sentido empregada para êsse fim.)
5.5352 Do mesmo modo, pretendeu-se exprimir "Não existe coisa alguma" por meio de "∼(∃x) . x = x". Ainda, porém, que isto fôsse uma proposição — esta não seria verdadeira se, com efeito, "houvesse coisas" que todavia não fossem idênticas consigo mesmas?
5.54 Na forma geral da proposição, a proposição aparece na proposição apenas como base das operações-verdades.
5.541 À primeira vista parece que seria possível uma proposição aparecer numa outra de outro modo.
Em particular em certas formas proposicionais da psicologia tais como "A acredita que p ocorre" ou "A pensa p", etc.
Nelas parece superficialmente que a proposição p se relaciona, de um certo modo, com um objeto A.
(E na moderna teoria do conhecimento (Russell, Moore, etc.) essas proposições são assim concebidas.)
5.542 É claro porém que "A acredita que p", "A pensa p", "A diz p" são da forma "p diz p". Não se trata aqui da coordenação de um fato e um objeto, mas da coordenação de fatos por meio da coordenação de seus objetos.
5.5421 Isto mostra que a alma — o sujeito, etc. — tal como é compreendida atualmente pela psicologia superficial, é um disparate.
Uma alma composta não seria mais alma.
5.5422 A explicação correta da forma da proposição "A julga p" deve indicar ser impossível julgar um absurdo. (A teoria de Russell não satisfaz essa condição.)
5.5423 Perceber um complexo quer dizer perceber que suas partes constituintes estão em relação entre si de um certo modo.
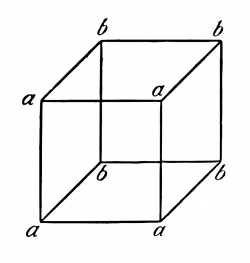
Isto também explica por que é possível ver a figura de duas maneiras como um cubo; e todos os fenômenos parecidos. Porquanto vemos realmente dois fatos diferentes.
(Primeiro vejo a partir dos vértices a, e só ligeiramente a partir de b; a aparece na frente; e vice-versa.)
5.55 Devemos agora a priori responder à pergunta a respeito de todas as formas possíveis de proposições elementares.
A proposição elementar constitui-se de nomes. Pôsto que não podemos dar o número de nomes com denotação diferente, não podemos também dar a composição das proposições elementares.
5.551 É nossa proposição básica: cada questão que em geral se deixa decidir pela lógica, deve sem mais deixar-se decidir.
(E se chegarmos à condição de precisar olhar o mundo para responder a tais problemas, isto mostraria que enveredamos por pistas bàsicamente falsas.)
5.552 A "experiência" que precisamos para compreender a lógica, não é a de que algo está do seguinte modo, mas a de que algo é; esta, porém, não é uma experiência.
A lógica está antes de qualquer experiência — de que algo é assim.
Dêsse modo está antes do Como mas não antes do Que.
5.5521 E se não fôsse assim como poderíamos aplicar a lógica? Poder-se-ia dizer: se houvesse uma lógica ainda que não houvesse um mundo, como poderia haver uma lógica já que há um mundo?
5.553 Russell disse que havia relações simples entre diversos números de coisas (individuais). Mas entre que números? E como isto há de ser decidido? — Por meio da experiência?
(Não existe um número excelente.)
5.554 A indicação daquelas formas especiais seria completamente arbitrária.
5.5541 Há de se revelar a priori se, por exemplo, posso chegar à condição de ter de designar alguma coisa com um signo de uma relação de 27 têrmos?
5.5542 Devemos, pois, fazer em geral tal pergunta? Podemos estabelecer uma forma em signos e não saber se a ela poderia corresponder alguma coisa?
Tem sentido a questão: O que deve ser a fim de que algo possa ocorrer?
5.555 É claro que temos da proposição elementar um conceito independente de sua forma lógica particular.
Onde é possível formar símbolos de acordo com um sistema, o importante do ponto de vista lógico é o próprio sistema, não o símbolo singular.
Como seria também possível que, na lógica, tivesse que me ocupar de formas que posso inventar? No entanto, devo ocupar-me com o que me torna possível inventá-las.
5.556 Não pode haver hierarquia de formas das proposições elementares. Podemos pressupor somente o que nós próprios construímos.
5.5561 A realidade empírica é limitada pela totalidade dos objetos. O limite reaparece na totalidade das proposições elementares.
As hierarquias são e devem ser independentes da realidade.
5.5562 Por motivos puramente lógicos sabemos que deve haver proposições elementares; dêsse modo, isto deve ser conhecido por todo aquêle que compreende as proposições na sua forma não-analisada.
5.5563 Tôdas as proposições de nossa linguagem corrente são, de fato, tais como são, perfeitamente ordenadas de um ponto de vista lógico. — Tudo o que fôr mais simples e que devemos aqui admitir não é símile da verdade mas a própria verdade plena.
(Nossos problemas não são abstratos mas talvez os mais concretos que existem.)
5.557 A aplicação da lógica decide que proposições elementares existem.
O que está na aplicação a lógica não pode antecipar.
É claro: a lógica não há de colidir com sua aplicação.
Mas a lógica deve referir-se à sua aplicação.
Dêsse modo, a lógica e sua aplicação não devem sobrepor-se uma à outra.
5.5571 Se não posso indicar a priori as proposições elementares, querer indicá-las deve redundar num patente absurdo.
5.6 Os limites de minha linguagem denotam os limites de meu mundo.
5.61 A lógica preenche o mundo, os limites do mundo são também seus limites.
Não podemos pois dizer na lógica: isto e isto existem no mundo, aquilo não.
Porquanto se pressuporia aparentemente que excluímos certas possibilidades, o que não pode ocorrer pois, do contrário, a lógica deveria colocar-se além dos limites do mundo, como se pudesse considerar êsses limites também do outro lado.
Não podemos pensar o que não podemos pensar, por isso também não podemos dizer o que não podemos pensar.
5.62 Esta observação dá a chave para decidir da questão: até onde o solipsismo é uma verdade.
O que o solipsismo nomeadamente acha é inteiramente correto, mas isto se mostra em vez de deixar-se dizer.
Que o mundo é o meu mundo, isto se mostra porque os limites da linguagem (da linguagem que sòmente eu compreendo) denotam os limites de meu mundo.
5.621 O mundo e a vida são um só.
5.63 Sou meu mundo. (O microcosmos.)
5.631 O sujeito representante e pensante não existe. Se escrevesse um livro: O mundo tal como encontro, deveria reportar-me a meu corpo e dizer quais membros estão sob minha vontade e quais não estão, etc. — isto é particularmente um método para isolar o sujeito, ou melhor, para indicar que não existe sujeito num sentido importante: dêle sozinho não é possível tratar neste livro.
5.632 O sujeito não pertence ao mundo mas é limite do mundo.
5.633 Onde no mundo se há de notar um sujeito metafísico?
Tu dizes que aqui se está inteiramente como diante do ôlho e do campo visual, mas tu não vês realmente o olho.
E não há coisa no campo visual que leve à conclusão de que ela é vista por um ôlho.
5.6331 O campo visual não tem nomeadamente uma forma como esta:
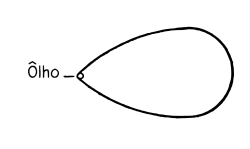
5.634 Isto se liga a que nenhuma parte de nossa experiência é a priori.
Tudo o que vemos poderia ser diferente.
Tudo o que podemos em geral descrever poderia ser diferente.
Não há a priori uma ordem das coisas.
5.64 Por aqui se vê que o solipsismo, levado às últimas conseqüências, coincide com o realismo puro. O eu do solipsismo reduz-se a um ponto sem exten- são, a realidade permanecendo coordenada a êle.
5.641 Tem, portanto, sentido real falar-se, na filosofia, do eu de um ponto de vista não-psicológico.
O eu penetra na filosofia porque o "mundo é meu mundo".
O eu filosófico não é o homem, nem o corpo humano, nem a alma humana de que se ocupa a psicologia, mas o sujeito metafísico, o limite — não sendo pois parte do mundo.
6 A forma geral da função de verdade é [math]\displaystyle{ [ \bar{p}, \bar{\xi}, N (\bar{\xi}) ] }[/math]
Esta é a forma geral da proposição.
6.001 Isto nada mais diz do que: cada proposição resulta da aplicação sucessiva da operação [math]\displaystyle{ N (\bar{\xi}) }[/math] sôbre as proposições elementares.
6.002 Dada a forma geral de como construir uma proposição, com isto já está dada a forma geral de como é possível gerar outra, por meio de uma operação, partindo-se de uma proposição.
6.01 A forma geral da operação [math]\displaystyle{ \Omega ' (\bar{\eta}) }[/math] é pois: [math]\displaystyle{ [\bar{\xi}, N(\bar{\xi})]' (\bar{\eta}) (= [ \bar{\eta}, \bar{\xi}, N (\bar{\xi}) ]) }[/math].
Esta é a forma mais geral da transposição de uma proposição para outra.
6.02 Chegamos assim aos números. Defino:
[math]\displaystyle{ x = \Omega^{0 \prime} x \text{ Def.} }[/math] e
[math]\displaystyle{ \Omega^{\prime} \Omega^{ \nu \prime} x = \Omega^{ \nu + 1 \prime} x \text{ Def.} }[/math]
Segundo essa regra de signos, escrevemos pois a série: [math]\displaystyle{ x, \Omega ' x, \Omega ' \Omega ' x, \Omega ' \Omega ' \Omega ' x, ..... }[/math]
como: [math]\displaystyle{ \Omega^{0 \prime} x, \Omega^{0+1 \prime} x, \Omega^{0 + 1 + 1 \prime} x, \Omega^{0 + 1 + 1 + 1 \prime} x, ..... }[/math]
Em vez de "[math]\displaystyle{ [ x, \xi, \Omega ' \xi ] }[/math]" escrevo, portanto,
"[math]\displaystyle{ [ \Omega^{0 \prime} x, \Omega^{ \nu \prime} x, \Omega^{ \nu + 1 \prime} x ] }[/math]".
E defino:
[math]\displaystyle{ 0 + 1 = 1 \text{ Def.} }[/math]
[math]\displaystyle{ 0 + 1 + 1 = 2 \text{ Def.} }[/math]
[math]\displaystyle{ 0 + 1 + 1 + 1 = 3 \text{ Def.} }[/math]
(e assim por diante)
6.021 O número é o expoente de uma operação.
6.022 O conceito de número nada mais é do que é comum a todos os números, a forma geral do número. O conceito número é a variável número.
E o conceito da igualdade entre os números é a forma geral de todas as igualdades especiais entre os números.
6.03 A forma geral dos números inteiros é: [0, ξ, ξ+1]. A teoria das classes é inteiramente supérflua para a matemática.
Isto está ligado a que a universalidade de que precisamos na matemática não é a acidental.
6.1 As proposições da lógica são tautologias.
- ↑ Os algarismos que enumeram as proposições isoladas indicam o peso lógico dessas proposições, a importância que adquirem em minha exposição. As proposições n.1, n.2, n.3, etc., constituem observações à proposição n.° n; as proposições n.m1, n.m2, etc., observações à proposição n.° n.m, e assim por diante.