Tractatus logico-philosophicus (visualizzazione ad albero)

[Espandi]1 Il mondo è tutto ciò che si verifica.

[Espandi]1.1 Il mondo è la totalità dei fatti, non delle cose.

1.11 Il mondo è determinato dai fatti e dal loro essere tutti i fatti.

1.12 Poiché la totalità dei fatti determina ciò che si verifica e anche tutto ciò che non si verifica.

1.13 I fatti nello spazio logico sono il mondo.

[Espandi]1.2 Il mondo si divide in fatti.

1.21 Qualcosa può verificarsi o non verificarsi e tutto il resto rimanere uguale.

[Espandi]2 Ciò che si verifica, il fatto, è il sussistere di stati di cose.

[Espandi]2.01 Lo stato di cose è un collegamento di oggetti (cose, entità).

2.011 È essenziale alla cosa poter essere parte costitutiva di uno stato di cose.

[Espandi]2.012 Nella logica niente è casuale: se la cosa può comparire nello stato di cose, allora la possibilità dello stato di cose dev'essere già implicata nella cosa.

2.0121 Sembrerebbe per così dire un caso se alla cosa, che di per sé potrebbe sussistere da sola, in seguito venisse adattato uno stato di cose.

Se le cose possono comparire negli stati di cose, allora questo deve già appartenere loro.

(Qualcosa di logico non può essere meramente possibile. La logica si occupa di ogni possibilità e tutte le possibilità sono i suoi fatti.)

Come non possiamo affatto rappresentarci oggetti spaziali al di fuori dello spazio, né temporali al di fuori del tempo, così non possiamo rappresentarci nessun oggetto al di fuori della possibilità del suo collegamento con altri.

Se posso rappresentarmi l'oggetto nel contesto dello stato di cose, allora non posso rappresentarmelo al di fuori della possibilità di questo contesto.

2.0122 La cosa è autosufficiente, nella misura in cui essa può comparire in tutti gli stati di cose possibili, ma questa forma di autosufficienza è una forma di connessione con lo stato di cose, una forma di non-autosufficienza. (È impossibile che le parole si presentino in due modi diversi, da sole e nella proposizione.)

[Espandi]2.0123 Se conosco l'oggetto, allora conosco anche tutte le possibilità del suo comparire in stati di cose.

(Ogni possibilità di questo genere deve appartenere alla natura dell'oggetto.)

Non si può scoprire in seguito una nuova possibilità.

2.01231 Per conoscere un oggetto non devo, certo, conoscere le sue proprietà esterne – ma devo conoscere tutte le sue proprietà interne.

2.0124 Se sono dati tutti gli oggetti, allora sono dati con ciò anche tutti i possibili stati di cose.

[Espandi]2.013 Ogni cosa è, per così dire, in uno spazio di stati di cose possibili. Posso rappresentarmi questo spazio vuoto, ma non la cosa senza lo spazio.

2.0131 L'oggetto spaziale deve trovarsi nello spazio infinito. (Il punto nello spazio è un posto per l'argomento [del predicato, della funzione].)

La macchia nel campo visivo non deve certo essere rossa, ma deve avere un colore: ha intorno a sé, in un certo senso, lo spazio dei colori. Il suono deve avere una altezza, l'oggetto del tatto una durezza ecc.

[Espandi]2.014 Gli oggetti contengono la possibilità di tutti gli stati di cose.

2.0141 La possibilità del suo comparire in stati di cose è la forma dell'oggetto.

[Espandi]2.02 L'oggetto è semplice.

2.0201 Ogni asserzione riguardante complessi può essere scomposta in una asserzione riguardante le loro parti costitutive e in quelle proposizioni che descrivono completamente i complessi.

[Espandi]2.021 Gli oggetti costituiscono la sostanza del mondo. Per questo non possono essere compositi.

2.0211 Se il mondo non avesse una sostanza, allora l'avere senso una proposizione dipenderebbe dall'essere vera un'altra proposizione.

2.0212 Sarebbe allora impossibile abbozzare un'immagine del mondo (non importa se vera o falsa).

2.022 È evidente che un mondo, per quanto diverso da quello reale venga concepito, deve avere qualcosa – una forma – in comune con il mondo reale.

[Espandi]2.023 Questa forma fissa consiste proprio degli oggetti.

2.0231 La sostanza del mondo può determinare soltanto una forma e nessuna proprietà materiale. Poiché queste proprietà si presentano solo attraverso le proposizioni – si costituiscono solo attraverso la configurazione degli oggetti.

2.0232 Detto incidentalmente: gli oggetti sono privi di colore.

[Espandi]2.0233 Due oggetti di forma logica uguale sono – a parte le loro proprietà esterne – distinti l'uno dall'altro solo dal loro essere diversi.

2.02331 O una cosa ha proprietà che nessun'altra ha, e allora si può senz'altro distinguerla dalle altre con una descrizione e indicarla; o invece vi sono più cose che hanno in comune tutte le loro proprietà, e allora è del tutto impossibile indicarne una tra le altre.

Poiché se la cosa non è individuata da niente, allora non posso individuarla, poiché altrimenti sarebbe appunto individuata.

2.024 La sostanza è ciò che sussiste indipendentemente da ciò che si verifica.

[Espandi]2.025 Essa è forma e contenuto.

2.0251 Spazio, tempo e colore (la proprietà dell'essere colorato) sono forme degli oggetti.

2.026 Solo se vi sono oggetti può esserci una forma fissa del mondo.

[Espandi]2.027 Ciò che è fisso, ciò che sussiste e l'oggetto sono uno.

2.0271 L'oggetto è ciò che è fisso, ciò che sussiste; la configurazione è ciò che è mutevole, instabile.

2.0272 La configurazione degli oggetti costituisce lo stato di cose.

[Espandi]2.03 Nello stato di cose gli oggetti sono connessi fra di loro, come gli anelli di una catena.

2.031 Nello stato di cose gli oggetti stanno in relazione l'uno con l'altro in modo determinato.

2.032 Il modo in cui gli oggetti sono reciprocamente connessi nello stato di cose è la struttura dello stato di cose.

2.033 La forma è la possibilità della struttura.

2.034 La struttura del fatto consiste delle strutture degli stati di cose.

2.04 La totalità degli stati di cose sussistenti è il mondo.

2.05 La totalità degli stati di cose sussistenti determina anche quali stati di cose non sussistono.

[Espandi]2.06 Il sussistere e il non-sussistere di stati di cose è la realtà.

(Il sussistere di stati di cose è da noi chiamato anche un fatto positivo, il non-sussistere un fatto negativo.)

2.061 Gli stati di cose sono indipendenti l'uno dall'altro.

2.062 Dal sussistere o non-sussistere di uno stato di cose non si possono trarre conclusioni circa il sussistere o non-sussistere di un altro.

2.063 La realtà nel suo complesso è il mondo.

[Espandi]2.1 Noi ci facciamo immagini dei fatti.

2.11 L'immagine rappresenta lo stato di cose nello spazio logico, il sussistere e non-sussistere degli stati cose.

2.12 L'immagine è un modello della realtà.

[Espandi]2.13 Agli oggetti corrispondono nell'immagine gli elementi dell'immagine.

2.131 Gli elementi dell'immagine stanno, nell'immagine, per gli oggetti.

[Espandi]2.14 L'immagine consiste nello stare in relazione l'uno con l'altro in modo determinato dei suoi elementi.

2.141 L'immagine è un fatto.

[Espandi]2.15 Lo stare in relazione l'uno con l'altro in modo determinato degli elementi dell'immagine rappresenta lo stare così in relazione l'una con l'altra delle cose.

Questa connessione degli elementi dell'immagine è chiamata la struttura dell'immagine e la possibilità di questa è chiamata la forma della raffigurazione dell'immagine.

[Espandi]2.151 La forma della raffigurazione è la possibilità che le cose stiano in relazione l'una con l'altra così come gli elementi dell'immagine.

2.1511 L'immagine è legata così alla realtà; essa raggiunge la realtà.

[Espandi]2.1512 L'immagine è come una misura applicata alla realtà.

2.15121 Solo i punti più esterni delle lineette di graduazione toccano l'oggetto da misurare.

2.1513 Secondo questa concezione, dunque, appartiene all'immagine anche la relazione raffigurativa che la rende un'immagine.

2.1514 La relazione raffigurativa consiste nelle coordinazioni degli elementi dell'immagine e delle cose.

2.1515 Queste coordinazioni sono, per così dire, i tentacoli degli elementi dell'immagine, con i quali l'immagine raggiunge la realtà.

[Espandi]2.16 Il fatto, per essere immagine, deve avere qualcosa in comune con il raffigurato.

2.161 Qualcosa dev'essere identico nell'immagine e nel raffigurato, affinché l'una possa essere un'immagine dell'altro.

[Espandi]2.17 Ciò che l'immagine deve avere in comune con la realtà per poterla raffigurare nel suo dato modo – corretto o errato – è la propria forma della raffigurazione.

2.171 L'immagine può raffigurare ogni realtà di cui ha la forma.

L'immagine spaziale tutto ciò che è spaziale, quella cromatica tutto ciò che è colorato, ecc.

2.172 L'immagine, tuttavia, non può raffigurare la propria forma della raffigurazione. Essa la esibisce.

2.173 L'immagine presenta il suo soggetto dall'esterno (il suo punto di vista è la sua forma della presentazione); perciò l'immagine presenta il suo soggetto in modo corretto o errato.

2.174 L'immagine non può tuttavia porsi al di fuori della sua forma della presentazione.

[Espandi]2.18 Ciò che ogni immagine, di qualunque forma, deve avere in comune con la realtà per poterla raffigurare – in modo corretto o errato – è la forma logica, cioè la forma della realtà.

2.181 Se la forma della raffigurazione è la forma logica, allora l'immagine è chiamata l'immagine logica.

2.182 Ogni immagine è anche un'immagine logica. (Per contro, non ogni immagine è ad es. un'immagine spaziale.)

2.19 L'immagine logica può raffigurare il mondo.

[Espandi]2.2 L'immagine ha in comune con il raffigurato la forma logica della raffigurazione.

2.201 L'immagine raffigura la realtà presentando una possibilità del sussistere e non-sussistere di stati di cose.

2.202 L'immagine presenta uno stato di cose possibile nello spazio logico.

2.203 L'immagine contiene la possibilità dello stato di cose che presenta.

2.21 L'immagine corrisponde alla realtà o no; è esatta o inesatta, vera o falsa.

[Espandi]2.22 L'immagine presenta ciò che presenta, indipendentemente dalla sua verità o falsità, attraverso la forma della raffigurazione.

2.221 Ciò che l'immagine presenta è il suo senso.

2.222 La sua verità o falsità sta nell'accordo o non-accordo del suo senso con la realtà.

2.223 Per stabilire se l'immagine è vera o falsa dobbiamo paragonarla con la realtà.

2.224 Dall'immagine da sola non si stabilisce se essa sia vera o falsa.

2.225 Non vi è un'immagine vera a priori.

[Espandi]3 L'immagine logica dei fatti è il pensiero.

3.001 «Uno stato di cose è pensabile» vuol dire: possiamo farci un'immagine di esso.

3.01 La totalità dei pensieri veri è un'immagine del mondo.

3.02 Il pensiero contiene la possibilità degli stati di cose che pensa. Ciò che è pensabile, è anche possibile.

[Espandi]3.03 Non possiamo pensare niente di illogico, perché altrimenti dovremmo pensare illogicamente.

3.031 Si diceva un tempo che Dio può creare tutto, tranne solo ciò che è contrario alle leggi logiche. – Noi in effetti non potremmo dire, di un mondo «illogico», che aspetto avrebbe.

[Espandi]3.032 Presentare nel linguaggio qualcosa «che contraddice la logica» è tanto impossibile quanto presentare nella geometria, attraverso le sue coordinate, una figura che contraddice le leggi dello spazio; oppure indicare le coordinate di un punto che non esiste.

3.0321 Possiamo ben presentare spazialmente uno stato di cose che vada contro le leggi della fisica, ma non uno che vada contro le leggi della geometria.

3.04 Un pensiero corretto a priori sarebbe un pensiero tale che la sua possibilità implicasse la sua verità.

3.05 Potremmo sapere a priori che un pensiero è vero solo se la sua verità si riconoscesse dal pensiero stesso (senza un termine di paragone).

[Espandi]3.1 Nella proposizione il pensiero si esprime in modo percepibile sensibilmente.

3.11 Utilizziamo il segno percepibile sensibilmente (segno vocale o grafico ecc.) della proposizione come proiezione dello stato di cose possibile.

Il metodo di proiezione è il pensare il senso della proposizione.

3.12 Chiamo il segno attraverso il quale esprimiamo il pensiero il segno proposizionale. E la proposizione è il segno proposizionale nella sua relazione proiettiva con il mondo.

3.13 Alla proposizione appartiene tutto ciò che appartiene alla proiezione; ma non il proiettato.

Quindi la possibilità di ciò che è proiettato, ma non ciò che è proiettato.

Nella proposizione, dunque, non è ancora contenuto il suo senso, ma vi è contenuta la possibilità di esprimerlo.

(«Il contenuto della proposizione» vuol dire il contenuto della proposizione dotata di senso.)

Nella proposizione è contenuta la forma del suo senso, ma non il suo contenuto.

[Espandi]3.14 Il segno proposizionale consiste nello stare in relazione l'uno con l'altro in modo determinato dei suoi elementi, le parole.

Il segno proposizionale è un fatto.

3.141 La proposizione non è un miscuglio di parole. – (Come il tema musicale non è un miscuglio di suoni.) La proposizione è articolata.

3.142 Solo i fatti possono esprimere un senso; una classe di nomi non può.

[Espandi]3.143 Che il segno proposizionale sia un fatto viene occultato dall'abituale forma espressiva della scrittura o della stampa.

Infatti nella proposizione stampata, ad es., il segno proposizionale non sembra essenzialmente diverso dalla parola.

(Per questo Frege ha potuto chiamare la proposizione un nome composto.)

3.1431 L'essenza del segno proposizionale diventa molto chiara se ce lo rappresentiamo come composto, anziché da segni grafici, da oggetti spaziali (come tavoli, sedie, libri).

La reciproca posizione spaziale di queste cose esprime allora il senso della proposizione.

3.1432 Non «il segno complesso “a R b” dice che a sta nella relazione R con b», bensì che «a» sta in una certa relazione con «b» dice che a R b.

3.144 Si possono descrivere gli stati di cose, non nominarli.

(I nomi assomigliano a punti, le proposizioni a frecce: esse hanno senso.)

[Espandi]3.2 Nella proposizione il pensiero può essere espresso in modo tale che gli elementi del segno proposizionale corrispondano agli oggetti del pensiero.

3.201 Chiamo questi elementi «segni semplici» e la proposizione «completamente analizzata».

3.202 I segni semplici usati nella proposizione si chiamano nomi.

3.203 Il nome significa l'oggetto. L'oggetto è il suo significato. («A» è lo stesso segno che «A».)

3.21 Alla configurazione dei segni semplici nel segno proposizionale corrisponde la configurazione degli oggetti nello stato di cose.

[Espandi]3.22 Il nome sta, nella proposizione, per l'oggetto.

3.221 Posso solo nominare gli oggetti. I segni stanno per essi. Posso solo parlare di essi, non posso asserirli. Una proposizione può dire solo come uno oggetto è, non cosa è.

3.23 Il requisito della possibilità dei segni semplici è il requisito della determinatezza del senso.

3.24 La proposizione che tratta di un complesso è in una relazione interna con la proposizione che tratta di una parte costituente del complesso.

Il complesso può essere dato solo attraverso la sua descrizione, e questa sarà esatta o non esatta. La proposizione nella quale si parla di un complesso non sarà, se questo non esiste, insensata, ma semplicemente falsa.

Che un elemento della proposizione designi un complesso si può vedere da un'indeterminatezza nelle proposizioni in cui tale elemento compare. Noi sappiamo che questa proposizione non determina ancora tutto. (La designazione della generalità contiene un archetipo.)

La sintesi del simbolo di un complesso in un simbolo semplice può essere espressa da una definizione.

[Espandi]3.25 Vi è una e una sola analisi completa della proposizione.

3.251 La proposizione esprime ciò che esprime in modi determinati, suscettibili di essere indicati chiaramente: la proposizione è articolata.

[Espandi]3.26 Il nome non può essere scomposto per mezzo di alcuna ulteriore definizione: esso è un segno primitivo.

3.261 Ogni segno definito designa attraverso quel segno da cui viene definito; e le definizioni mostrano la via.

Due segni, un segno primitivo e uno definito attraverso segni primitivi, non possono designare nello stesso modo. Non si possono dissezionare i nomi attraverso definizioni. (Né alcun segno che da solo e in modo indipendente ha un significato.)

3.262 Ciò che nei segni non giunge a espressione viene mostrato dal loro uso. Ciò che i segni nascondono è enunciato dal loro uso.

3.263 I significati dei segni primitivi possono essere chiariti attraverso spiegazioni. Le spiegazioni sono proposizioni che contengono i segni primitivi. Dunque possono essere comprese solo se i significati di questi segni sono già conosciuti.

[Espandi]3.3 Solo la proposizione ha senso; solo nel contesto della proposizione un nome ha significato.

[Espandi]3.31 Chiamo ogni parte della proposizione che caratterizza il suo senso un'espressione (un simbolo).

(La proposizione stessa è un'espressione.)

È espressione tutto ciò di essenziale per il senso della proposizione che le proposizioni possono avere in comune tra di loro.

L'espressione caratterizza una forma e un contenuto.

3.311 L'espressione presuppone le forme di tutte le proposizioni in cui può comparire. Essa è il tratto caratteristico comune di una classe di proposizioni.

3.312 Essa è dunque presentata dalla forma generale delle proposizioni che essa caratterizza.

Infatti in questa forma l'espressione sarà costante, e tutto il resto variabile.

3.313 L'espressione è quindi presentata da una variabile i cui valori sono le proposizioni che contengono l'espressione.

(Nel caso limite le variabili divengono costanti, l'espressione diviene proposizione.)

Chiamo una tale variabile «variabile proposizionale».

3.314 L'espressione ha significato solo nella proposizione. Ogni variabile può essere intesa come variabile proposizionale.

(Incluso il nome variabile.)

3.315 Se trasformiamo una parte costitutiva di una proposizione in una variabile, otteniamo una classe di proposizioni che costituiscono tutti i valori della proposizione variabile così ottenuta. Questa classe dipende ancora, in generale, da ciò che noi intendiamo, per convenzione arbitraria, mediante le parti di quella proposizione. Se però trasformiamo in variabili tutti quei segni il cui significato è determinato arbitrariamente, otteniamo ancora e sempre una tale classe. Questa, tuttavia, non dipende più da alcuna convenzione, ma solo dalla natura della proposizione. Essa corrisponde a una forma logica – a un archetipo logico.

3.316 Quali valori sia possibile assumere per la variabile proposizionale è qualcosa che viene fissato.

La fissazione dei valori è la variabile.

3.317 La fissazione dei valori delle variabili proposizionali è l'indicazione delle proposizioni il cui tratto comune è la variabile.

La fissazione è una descrizione di queste proposizioni.

La fissazione quindi tratterà solo di simboli, non del loro significato.

E solo questo è essenziale a tale fissazione: che essa è solo una descrizione di simboli e non dice niente sul simbolizzato.

Come avviene la descrizione delle proposizioni è inessenziale.

3.318 Intendo la proposizione – come Frege e Russell – come funzione delle espressioni in essa contenute.

[Espandi]3.32 Il segno è ciò che nel simbolo è percepibile sensibilmente.

3.321 Due simboli diversi possono quindi avere il segno in comune tra loro (segno grafico o segno vocale ecc.) – essi simbolizzano allora in modo diverso.

3.322 Che noi li simbolizziamo con lo stesso segno ma con due diversi modi di simbolizzazione non può mai indicare il tratto comune di due oggetti. Il segno, infatti, è arbitrario. Si potrebbero quindi anche scegliere due segni diversi, e allora che ne sarebbe di ciò che vi è in comune nella simbolizzazione?

3.323 Nel linguaggio comune capita spessissimo che la stessa parola simbolizzi in diversi modi – che dunque appartenga a diversi simboli – o che due parole che simbolizzano in modi diversi vengano impiegate in modo esteriormente identico nella proposizione.

Così la parola «è» compare come copula, come segno di identità e come espressione dell'esistenza; «esistere» come verbo intransitivo alla stessa stregua di «andare»; «identico» come aggettivo; parliamo di un qualcosa, ma anche dell'accadere di qualcosa.

(Nella proposizione «Rosa è rosa» – dove la prima parola è un nome di persona, l'ultima un aggettivo – queste parole non hanno semplicemente diverso significato, ma sono simboli diversi.)

3.324 Così nascono facilmente gli equivoci più fondamentali (dei quali tutta la filosofia è piena).

3.325 Per sottrarci a questi errori dobbiamo impiegare un linguaggio segnico che li esclude, non impiegando lo stesso segno in simboli diversi e non impiegando esteriormente nello stesso modo segni che simbolizzano in modo diverso. Un linguaggio segnico, dunque, che obbedisce alla grammatica logica – la sintassi logica.

(L'ideografia di Frege e Russell è un tale linguaggio, che tuttavia non esclude ancora tutti gli errori.)

3.326 Per riconoscere il simbolo nel segno bisogna prenderne in considerazione l'uso dotato di senso.

3.327 Solo insieme con la sua applicazione logico-sintattica il segno determina una forma logica.

3.328 Se un segno non viene usato, allora è privo di significato. Questo è il senso del rasoio di Occam.

(Se tutto sta come se un segno avesse significato, allora esso ha significato.)

[Espandi]3.33 Nella sintassi logica il significato di un segno non può mai avere un ruolo; esso deve poter essere stabilito senza che in ciò si parli del significato di un segno; esso può presupporre solo la descrizione delle espressioni.

3.331 A partire da questa osservazione volgiamo lo sguardo alla «theory of types» di Russell: l'errore di Russell si mostra nella necessità in cui egli si è trovato, al momento di stabilire le regole relative ai segni, di parlare del significato dei segni.

3.332 Nessuna proposizione può enunciare qualcosa su se stessa, poiché il segno proposizionale non può essere contenuto in sé stesso (questa è l'intera «theory of types»).

3.333 Una funzione, quindi, non può essere il proprio stesso argomento, poiché il segno di funzione contiene già l'archetipo del suo argomento e non può contenere se stesso.

Assumiamo infatti che la funzione F (f x) possa essere il proprio stesso argomento; allora si darebbe una proposizione «F (F (f x))», ma in questa la funzione F esterna e la funzione F interna devono avere significati diversi, poiché quella interna ha la forma φ (f x), quella esterna la forma ψ (φ (f x)). In comune a entrambe le funzioni vi è solo la lettera «F», che però da sola non simbolizza niente.

Questo diventa subito chiaro se anziché «F (F (u))» scriviamo «(∃ φ) : F (φ u) . φ u = F u».

Con ciò si risolve il paradosso di Russell.

3.334 Le regole della sintassi logica devono comprendersi da sé, purché si sappia come ogni dato segno designa.

[Espandi]3.34 La proposizione possiede tratti essenziali e accidentali.

Accidentali sono i tratti che derivano dal particolare modo in cui viene prodotto il segno proposizionale. Essenziali quelli senza i quali la proposizione non sarebbe capace di esprimere il suo senso.

[Espandi]3.341 L'essenziale nella proposizione è dunque ciò che è comune a tutte le proposizioni che possono esprimere lo stesso senso.

E allo stesso modo, in generale, l'essenziale nel simbolo è ciò che hanno in comune tutti i simboli che possono assolvere lo stesso scopo.

3.3411 Si potrebbe quindi dire: il nome, propriamente, è ciò che tutti i simboli che designano l'oggetto hanno in comune. Si rivelerebbe così gradualmente che nessuna composizione è minimamente essenziale per il nome.

[Espandi]3.342 Nelle nostre notazioni qualcosa è, certo, arbitrario, ma questo non è arbitrario: che se abbiamo determinato qualcosa arbitrariamente, allora qualcosa d'altro deve verificarsi. (Questo dipende dall'essenza della notazione.)

3.3421 Una particolare modalità di designazione può non essere importante, ma è sempre importante che essa sia una possibile modalità di designazione. E così stanno le cose nella filosofia in generale: l'individuo si rivela sempre di nuovo non importante, ma la possibilità di ogni individuo ci rivela qualcosa sull'essenza del mondo.

3.343 Le definizioni sono regole per la traduzione di un linguaggio in un altro. Ogni linguaggio segnico corretto deve poter essere tradotto in ogni altro secondo tali regole: questo è ciò che essi hanno tutti in comune.

[Espandi]3.344 Ciò che nel simbolo designa è ciò che vi è di comune in tutti quei simboli con cui esso può essere sostituito secondo le regole della sintassi logica.

3.3441 Si può ad es. esprimere così ciò che vi è di comune in tutte le notazioni per le funzioni di verità: a esse è comune il poter essere tutte sostituite – ad es. – dalla notazione di «~p» («non p») e «p ∨ q» («p o q»).

(Ecco il modo in cui una particolare notazione possibile può rivelarci qualcosa di generale.)

3.3442 Anche il segno del complesso si risolve tramite l'analisi in modo non arbitrario, cosicché la sua scomposizione sarebbe diversa per ogni struttura della proposizione.

[Espandi]3.4 La proposizione determina un luogo nello spazio logico. L'esistenza di questo luogo logico non è garantita che dall'esistenza delle parti costituenti, dall'esistenza della proposizione dotata di senso.

[Espandi]3.41 Il segno proposizionale e le coordinate logiche: questo è il luogo logico.

3.411 Il luogo geometrico e quello logico corrispondono in quanto sono entrambi la possibilità di un'esistenza.

3.42 Benché la proposizione possa determinare solo un luogo dello spazio logico, con essa dev'essere già dato l'intero spazio logico.

(Altrimenti con la negazione, la somma logica, il prodotto logico ecc. verrebbero introdotti sempre nuovi elementi – in coordinazione.)

(L'impalcatura logica intorno all'immagine determina lo spazio logico. La proposizione attraversa tutto lo spazio logico.)

3.5 Il segno proposizionale applicato, pensato, è il pensiero.

[Espandi]4 Il pensiero è la proposizione dotata di senso.

4.001 La totalità delle proposizioni è il linguaggio.

4.002 L'uomo possiede la capacità di costruire linguaggi, mediante i quali può essere espresso qualsiasi senso, senza avere un'idea di come e cosa ogni parola significa. – Così come si parla senza sapere come sono prodotti i singoli suoni.

Il linguaggio comune è una parte dell'organismo umano e non è meno complicato di quest'ultimo.

È umanamente impossibile dedurne in modo immediato la logica del linguaggio.

Il linguaggio traveste il pensiero. Di modo che non si può concludere dalla forma esteriore del vestito alla forma del pensiero sotto il vestito; perché la forma esteriore del vestito è fatta per tutt'altri scopi che quello di permettere di riconoscere la forma del corpo.

Gli accordi taciti per la comprensione del linguaggio comune sono enormemente complessi.

[Espandi]4.003 Le tesi e le domande su cose filosofiche che sono state messe per iscritto sono per la maggior parte non false, ma insensate. Perciò non possiamo affatto rispondere a domande di tal sorta, ma solo stabilire la loro insensatezza. Le domande e le proposizioni dei filosofi nascono per la maggior parte dall'incomprensione della logica del nostro linguaggio.

(Esse sono domande dello stesso tipo di quella se il buono sia o meno lo stesso che il bello.)

E non è stupefacente che i problemi più profondi propriamente non siano problemi.

4.0031 Tutta la filosofia è «critica del linguaggio». (Non tuttavia nel senso di Mauthner.) È merito di Russell aver mostrato che la forma logica apparente della proposizione può non essere la sua forma logica reale.

[Espandi]4.01 La proposizione è un'immagine della realtà.

La proposizione è un modello della realtà così come ce la rappresentiamo.

4.011 A prima vista la proposizione – come essa per esempio sta stampata sulla carta – non sembra essere un'immagine della realtà di cui tratta. Ma anche la notazione musicale a prima vista non sembra essere un'immagine della musica, e la nostra notazione fonetica o alfabetica non sembra essere un'immagine del nostro linguaggio vocale.

E tuttavia questi linguaggi segnici si rivelano, anche nel senso abituale, come immagini di ciò che presentano.

4.012 È evidente che percepiamo una proposizione della forma «a R b» come immagine. Qui il segno è evidentemente qualcosa di rassomigliante al designato.

4.013 E se penetriamo nell'essenziale di questa natura figurativa vediamo che essa non viene compromessa da apparenti irregolarità (come l'impiego del ♯ e del ♭ nella notazione musicale).

Poiché anche queste irregolarità raffigurano ciò che devono esprimere; solo in modo diverso.

[Espandi]4.014 Il disco del grammofono, il pensiero musicale, la notazione musicale, le onde sonore stanno tutti tra di loro in quella relazione interna di raffigurazione che sussiste tra linguaggio e mondo.

A tutti è comune la costruzione logica.

(Come nella fiaba i due giovani, i loro due cavalli e i loro gigli. Essi sono tutti in un certo senso uno.)

4.0141 Che vi sia una regola generale mediante la quale il musicista può trarre la sinfonia dalla partitura, e che ve ne sia una mediante la quale si può trarre dal solco del disco per il grammofono la sinfonia e poi, secondo la prima regola, di nuovo dedurre la partitura – in questo appunto consiste la somiglianza interna di queste forme apparentemente così diverse. E questa regola è la legge della proiezione che proietta la sinfonia nel linguaggio della notazione musicale. È la regola della traduzione del linguaggio della notazione musicale nel linguaggio del disco del grammofono.

4.015 La possibilità di tutte le immagini, di tutta la natura figurativa del nostro modo di espressione, risiede nella logica della raffigurazione.

4.016 Per comprendere l'essenza della proposizione, pensiamo alla scrittura geroglifica, che raffigura i fatti che descrive.

E da essa si è sviluppata la scrittura alfabetica, senza che l'essenziale della raffigurazione andasse perso.

[Espandi]4.02 Lo vediamo da questo: che comprendiamo il senso del segno proposizionale senza che esso ci sia stato spiegato.

4.021 La proposizione è un'immagine della realtà: poiché se comprendo la proposizione conosco lo stato di cose da essa presentato. E comprendo la proposizione senza che il suo senso mi sia stato spiegato.

4.022 La proposizione mostra il suo senso.

La proposizione mostra come le cose stanno se è vera. E dice che stanno così.

4.023 La realtà deve essere fissata mediante la proposizione per il sì o per il no.

A questo scopo la realtà deve essere descritta completamente dalla proposizione.

La proposizione è la descrizione di uno stato di cose.

Come la descrizione di un oggetto lo descrive secondo le sue proprietà esterne, così la proposizione descrive la realtà secondo le sue proprietà interne.

La proposizione costruisce un mondo con l'aiuto di un'impalcatura logica, e perciò dalla proposizione si può anche vedere come sta tutto ciò che logicamente ne consegue se essa è vera. Si possono trarre conclusioni da una proposizione falsa.

4.024 Comprendere una proposizione vuol dire sapere cosa accade se essa è vera.

(La si può quindi comprendere senza sapere se è vera.)

La si comprende quando si comprendono le sue parti costituenti.

4.025 La traduzione di un linguaggio in un altro non procede traducendo ogni proposizione dell'uno in una proposizione dell'altro; bensì vengono tradotte solo le parti costituenti.

(E il vocabolario non traduce solo i sostantivi, ma anche verbi, aggettivi, congiunzioni ecc.; e li tratta tutti allo stesso modo.)

4.026 I significati dei segni semplici (delle parole) devono esserci spiegati affinché li comprendiamo.

Con le proposizioni invece ci spieghiamo.

4.027 Fa parte dell'essenza della proposizione che essa possa comunicarci un senso nuovo.

[Espandi]4.03 Una proposizione deve comunicare un senso nuovo con vecchie espressioni.

La proposizione ci comunica uno stato di cose; quindi dev'essere essenzialmente connessa con lo stato di cose.

E la connessione consiste appunto in questo: che la proposizione è l'immagine logica dello stato di cose.

La proposizione asserisce qualcosa solo in quanto è un'immagine.

[Espandi]4.031 Nella proposizione uno stato di cose viene, per dir così, messo insieme a titolo di prova.

Si potrebbe addirittura dire, invece che «questa proposizione ha questo e questo senso», «questa proposizione presenta questo e questo stato di cose».

4.0311 Se un nome sta per una cosa, un altro per un'altra cosa ed essi sono collegati l'uno all'altro, allora l'insieme – come un tableau vivant – rappresenta lo stato di cose.

4.0312 La possibilità della proposizione riposa sul principio che i segni stanno per gli oggetti.

Il mio pensiero fondamentale è che le «costanti logiche» non stanno per alcunché. Che niente può stare per la logica dei fatti.

4.032 La proposizione è un'immagine di uno stato di cose solo in quanto essa è logicamente organizzata.

(Anche la proposizione «ambulo» è composta, poiché la sua radice dà un altro senso con un'altra desinenza, e la sua desinenza con un'altra radice.)

[Espandi]4.04 Nella proposizione dev'essere differenziato esattamente tanto quanto è differenziato nello stato di cose che essa presenta.

Entrambi devono possedere la stessa molteplicità logica (matematica). (Vedi la Meccanica di Hertz a proposito dei modelli dinamici.)

[Espandi]4.041 Questa stessa molteplicità matematica non si può, naturalmente, raffigurare a sua volta. Da essa non si può uscire finché si raffigura.

4.0411 Se volessimo ad es. esprimere ciò che esprimiamo attraverso «(x).f x» attraverso l'anteposizione di un indice a «f x» – ad es. così: «gen. f x» – ciò non sarebbe sufficiente – non sapremmo che cosa viene generalizzato. Se volessimo indicarlo attraverso un indice «g» – ad es. così: «f (x_g)» – anche ciò non sarebbe sufficiente – non conosceremmo il dominio della designazione della generalità.

Se volessimo cercare di farlo attraverso l'introduzione di un indice nei posti per l'argomento – per esempio così: «(G, G) . F (G, G)» – ciò non sarebbe sufficiente – non potremmo stabilire l'identità delle variabili. E così via.

Tutti questi modi di designazione non sono sufficienti perché essi non hanno la necessaria molteplicità matematica.

4.0412 Per la stessa ragione la spiegazione idealistica della visione delle relazioni spaziali attraverso gli «occhiali spaziali» non è sufficiente, poiché essa non riesce a spiegare la molteplicità di queste relazioni.

4.05 La realtà viene confrontata con la proposizione.

[Espandi]4.06 La proposizione può essere vera o falsa solo essendo un'immagine della realtà.

4.061 Se non si considera che la proposizione ha un senso indipendente dai fatti, allora si può facilmente credere che vero e falso siano relazioni tra segno e designato a eguale titolo.

Allora si potrebbe dire ad es. che «p» designa in modo vero ciò che «~p» designa in modo falso, ecc.

[Espandi]4.062 Si può comunicare con proposizioni false, come finora si è fatto con proposizioni vere? Purché si sappia che esse sono intese come false. No! Poiché una proposizione è vera quando le cose stanno come noi diciamo attraverso essa; e se con «p» intendiamo ~p e le cose stanno come noi intendiamo, allora «p» nella nuova concezione è vera, e non falsa.

4.0621 È però importante che il segno «p» e «~p» possano dire lo stesso. Poiché ciò mostra che al segno «~» non corrisponde niente nella realtà.

Che in una proposizione compaia la negazione non è ancora un'indicazione del suo senso (~~p = p).

Le proposizioni «p» e «~p» hanno senso contraddittorio, ma corrisponde loro una e la stessa realtà.

4.063 Un'immagine per spiegare il concetto di verità: macchia nera su carta bianca; la forma della macchia si può descrivere dichiarando per ogni punto della superficie se esso è bianco o nero. Al fatto che un punto sia nero corrisponde un fatto positivo, al fatto che un punto sia bianco (non nero) un fatto negativo. Se indico un punto della superficie (un valore di verità, nei termini di Frege), questo corrisponde all'assunzione che viene offerta al giudizio, ecc. ecc.

Tuttavia per poter dire che un punto è nero o bianco devo prima sapere quando un punto si chiama nero e quando lo si chiama bianco; per poter dire che «p» è vera (o falsa) devo aver determinato in quali circostanze chiamo «p» vera, e così facendo determino il senso della proposizione.

Ora, il punto in cui la similitudine zoppica è questo: possiamo indicare un punto del foglio anche senza sapere che cosa è bianco e cosa nero; a una proposizione senza senso però non corrisponde proprio niente, poiché essa non designa alcuna cosa (valore di verità) le cui proprietà si chiamino per esempio «falso» o «vero»; il verbo di una proposizione non è – come credeva Frege – «è vero» o «è falso», bensì ciò che «è vero» deve già contenere il verbo.

[Espandi]4.064 Ogni proposizione deve già avere un senso; l'affermazione non può darglielo, poiché essa afferma appunto il senso. E lo stesso vale per la negazione, ecc.

4.0641 Si potrebbe dire: la negazione è già correlata al luogo logico che la proposizione negata determina.

La proposizione che nega determina un altro luogo logico rispetto alla proposizione negata.

La proposizione che nega determina un luogo logico con l'aiuto del luogo logico della proposizione negata, descrivendo il primo come collocato al di fuori del secondo.

Che si possa negare di nuovo la proposizione negata basta per mostrare che ciò che viene negato è già una proposizione, e non solo la bozza di una proposizione.

[Espandi]4.1 La proposizione [rap]presenta il sussistere e non-sussistere degli stati di cose.

[Espandi]4.11 La totalità delle proposizioni vere è l'intera scienza della natura (o la totalità delle scienze della natura).

4.111 La filosofia non è una delle scienze della natura.

(La parola «filosofia» deve significare qualcosa che sta sopra o sotto, ma non accanto, alle scienze della natura.)

[Espandi]4.112 Lo scopo della filosofia è la chiarificazione logica dei pensieri.

La filosofia non è una teoria, ma un'attività.

Un'opera filosofica consiste essenzialmente di chiarificazioni.

La filosofia non dà come risultato «proposizioni filosofiche», ma il chiarificarsi di proposizioni.

La filosofia deve rendere chiari pensieri che altrimenti sono, per così dire, nebulosi e sfocati, e delimitarli precisamente.

4.1121 La psicologia non è imparentata con la filosofia più di qualsiasi altra scienza della natura.

La teoria della conoscenza è la filosofia della psicologia.

Il mio studio dei linguaggi segnici non corrisponde allo studio dei processi di pensiero, che i filosofi consideravano così essenziale per la filosofia della logica? Solamente, essi si impelagarono perlopiù in ricerche psicologiche inessenziali, e vi è un pericolo analogo anche per il mio metodo.

4.1122 La teoria darwiniana non ha a che fare con la filosofia più di ogni altra ipotesi della scienza naturale.

4.113 La filosofia delimita l'area [di ciò che è] problematizzabile [da parte] della scienza naturale.

4.114 Essa deve circoscrivere il pensabile e, con ciò, l'impensabile.

Deve delimitare l'impensabile dall'interno, attraverso il pensabile.

4.115 Essa significherà l'indicibile presentando chiaramente il dicibile.

4.116 Tutto ciò che può essere affatto pensato può essere pensato chiaramente. Tutto ciò che può essere detto può essere detto chiaramente.

[Espandi]4.12 La proposizione può presentare l'intera realtà, ma non può presentare ciò che essa deve avere in comune con la realtà per poterla presentare – la forma logica.

Per poter presentare la forma logica dovremmo poterci porre con la proposizione al di fuori della logica, cioè al di fuori del mondo.

[Espandi]4.121 La proposizione non può presentare la forma logica; questa si rispecchia nella proposizione.

Ciò che si rispecchia nel linguaggio non può essere presentato dal linguaggio.

Ciò che si esprime nel linguaggio non può essere espresso da noi mediante il linguaggio.

La proposizione mostra la forma logica della realtà.

La esibisce.

4.1211 Così una proposizione «f a» mostra che nel suo senso compare l'oggetto a; due proposizioni «f a» e «g a» che in entrambe si parla dello stesso oggetto.

Se due proposizioni si contraddicono a vicenda, questo è mostrato dalla loro struttura; lo stesso se esse seguono una dall'altra. E così via.

4.1212 Ciò che può essere mostrato non può essere detto.

4.1213 Ora comprendiamo anche questo nostro sentimento: che saremmo in possesso di una concezione logica corretta se solo nel nostro linguaggio segnico tutto funzionasse.

[Espandi]4.122 Possiamo parlare, in un certo senso, di proprietà formali degli oggetti e degli stati di cose, ovvero di proprietà della struttura dei fatti, e, nello stesso senso, di relazioni formali e di relazioni di strutture.

(Anziché «proprietà della struttura» dico anche «proprietà interna»; anziché «relazione delle strutture», «relazione interna».

Introduco queste espressioni per mostrare la ragione della confusione, molto comune tra i filosofi, tra le relazioni interne e le relazioni vere e proprie (esterne).)

Il sussistere di certe proprietà e relazioni interne non può tuttavia essere asserito mediante proposizioni; esso si mostra invece nelle proposizioni che presentano quegli stati di cose e vertono su quegli oggetti.

4.1221 Una proprietà interna di un fatto può anche essere chiamata un tratto di questo fatto. (Nel senso in cui parliamo per esempio di tratti di un viso.)

4.123 Una proprietà è interna se è impensabile che il suo oggetto non la possieda.

(Questo colore blu e quello stanno eo ipso nella relazione interna di più chiaro e più scuro. È impensabile che questi due oggetti non stiano in questa relazione.)

(Qui all'uso oscillante delle parole «proprietà» e «relazione» corrisponde l'uso oscillante della parola «oggetto».)

[Espandi]4.124 Il sussistere di una proprietà interna di uno stato di cose possibile non viene espresso attraverso una proposizione, bensì si esprime nella proposizione che presenta lo stato di cose attraverso una proprietà interna di questa proposizione.

Affermare che la proposizione ha una proprietà formale sarebbe tanto insensato quanto negarlo.

4.1241 Non si possono distinguere le forme una dall'altra dicendo che questa ha questa proprietà, l'altra invece quella; poiché ciò presuppone che abbia un senso affermare entrambe le proprietà di entrambe le forme.

[Espandi]4.125 Il sussistere di una relazione interna tra stati di cose possibili si esprime linguisticamente attraverso una relazione interna tra le proposizioni che li presentano.

4.1251 Qui si risolve la disputa «se tutte le relazioni siano interne o esterne».

4.1252 Chiamo serie formali quelle serie che sono ordinate attraverso relazioni interne.

La serie dei numeri non è ordinata secondo una relazione esterna, ma secondo una relazione interna.

Analogamente la serie delle proposizioni

«a R b»,

«(∃x) : a R x . x R b»,

«(∃x, y) : a R x . x R y . y R b», e così di seguito.

(Se b sta in una di queste relazioni ad a, allora chiamo b un successore di a.)

4.126 Nel senso in cui parliamo di proprietà formali possiamo ora parlare anche di concetti formali.

(Introduco questa espressione per rendere chiara la ragione della confusione dei concetti logici con i concetti veri e propri, la quale attraversa tutta la vecchia logica.)

Che qualcosa cada sotto un concetto formale come suo oggetto non può essere espresso mediante una proposizione. Ciò si mostra invece nel segno di questo oggetto stesso. (Il nome mostra di designare un oggetto, il segno numerico di designare un numero ecc.)

I concetti formali non possono essere presentati, come i concetti veri e propri, attraverso una funzione.

Poiché i loro caratteri, le proprietà formali, non vengono espressi attraverso funzioni.

L'espressione della proprietà formale è un tratto di certi simboli.

Il segno dei caratteri di un concetto formale è quindi un tratto distintivo di tutti i simboli i cui significati cadono sotto il concetto.

L'espressione del concetto formale dunque è una variabile proposizionale in cui solo questo tratto caratteristico è costante.

[Espandi]4.127 La variabile proposizionale designa il concetto formale e i suoi valori gli oggetti che cadono sotto questo concetto.

4.1271 Ogni variabile è il segno di un concetto formale.

Ogni variabile infatti presenta una forma costante che tutti i suoi valori possiedono, e che può essere considerata una proprietà formale di questi valori.

[Espandi]4.1272 Perciò il nome variabile «x» è il segno proprio dello pseudo-concetto oggetto.

Ovunque la parola «oggetto» («cosa», «entità», ecc.) viene impiegata correttamente, essa nell'ideografia viene espressa attraverso il nome variabile.

Per esempio nella proposizione «vi sono 2 oggetti che…» attraverso «(∃x, y)…».

Ovunque viene impiegata diversamente, cioè come parola che indica un concetto vero e proprio, si originano pseudo-proposizioni insensate.

Così ad es. non si può dire «vi sono oggetti» come si dice «vi sono libri». E allo stesso modo non si può dire «vi sono 100 oggetti» o «vi sono ℵ₀ oggetti». Ed è insensato parlare del numero di tutti gli oggetti.

Lo stesso vale per le parole «complesso», «fatto», «funzione», «numero», ecc.

Esse simbolizzano tutte concetti formali e vengono presentate nell'ideografia attraverso variabili, non (come pensavano Frege e Russell) attraverso funzioni o classi.

Espressioni come «1 è un numero», «vi è un solo zero» e tutte quelle di questo genere sono insensate.

(Dire «vi è un solo 1» è tanto insensato quanto lo sarebbe dire: «2 + 2 è uguale a 4 alle ore 3».)

4.12721 Il concetto formale è già dato con un oggetto che cade sotto di esso. Non si possono quindi introdurre, come concetti fondamentali, gli oggetti che cadono sotto un concetto formale e il concetto formale stesso. Non si possono quindi ad es. introdurre, come concetti fondamentali, il concetto della funzione e anche funzioni particolari (come fa Russell); o il concetto di numero e numeri determinati.

4.1273 Se vogliamo esprimere la proposizione generale «b è un successore di a» nell'ideografia, abbiamo bisogno per questo di un'espressione per il termine generale della serie formale:

a R b,

(∃x) : a R x . x R b,

(∃x y) : a R x . x R y . y R b, …

Il termine generale di una serie formale può essere espresso solo mediante una variabile, poiché il concetto di termine di questa serie formale è un concetto formale. (Questo è stato trascurato da Frege e Russell; il modo in cui essi vogliono esprimere le proposizioni generali, come quella qui sopra, è perciò errato; esso contiene un circolo vizioso.)

Possiamo determinare il termine generale della serie formale indicando il suo primo termine e la forma generale dell'operazione che genera l'elemento successivo dalla proposizione precedente.

4.1274 La domanda sull'esistenza di un concetto formale è insensata. Poiché nessuna proposizione può rispondere a una tale domanda.

(Così ad es. non si può chiedere: «Vi sono proposizioni soggetto-predicato inanalizzabili?»)

4.128 Le forme logiche sono anumeriche.

Perciò nella logica non vi sono numeri speciali e perciò non vi è alcun monismo filosofico o dualismo filosofico ecc.

[Espandi]4.2 Il senso della proposizione è il suo accordo e non-accordo con le possibilità del sussistere e non-sussistere degli stati di cose.

[Espandi]4.21 La proposizione più semplice, la proposizione elementare, asserisce il sussistere di uno stato di cose.

4.211 Una caratteristica della proposizione elementare è che nessuna proposizione elementare può contraddirla.

[Espandi]4.22 La proposizione elementare consiste di nomi. Essa è una connessione, una concatenazione di nomi.

[Espandi]4.221 È evidente che tramite l'analisi della proposizione dobbiamo pervenire a proposizioni elementari che consistano di nomi collegati gli uni agli altri in modo immediato.

Si pone qui la questione di come si costituisca la connessione proposizionale.

4.2211 Anche se il mondo fosse infinitamente complesso, così che ogni fatto consistesse di un numero infinito di stati di cose e ogni stato di cose fosse composto di un numero infinito di oggetti, anche in questo caso dovrebbero esservi oggetti e stati di cose.

4.23 Il nome compare nella proposizione solo nel contesto della proposizione elementare.

[Espandi]4.24 I nomi sono i simboli semplici; li indico mediante singole lettere («x», «y», «z»).

Scrivo la proposizione elementare come funzione dei nomi nella forma: «f x», «φ (x, y)», ecc.

Oppure la indico mediante le lettere p, q, r.

4.241 Se utilizzo due segni in un solo e medesimo significato, lo esprimo collocando tra essi il segno «=».

«a = b» vuol dire quindi: il segno «a» può essere sostituito con il segno «b».

(Se introduco un nuovo segno «b» attraverso un'uguaglianza, stabilendo che esso debba sostituire un segno «a» già noto, allora (come Russell) scrivo l'uguaglianza – definizione – nella forma «a = b def.». La definizione è una regola segnica.)

4.242 Espressioni della forma «a = b» sono quindi solo espedienti della presentazione; esse non dicono nulla sul significato dei segni «a», «b».

4.243 Possiamo comprendere due nomi senza sapere se essi simbolizzano la stessa cosa o due cose diverse? – Possiamo comprendere una proposizione in cui compaiono due nomi senza sapere se il loro significato è uguale o diverso?

Se per esempio conosco il significato di una parola inglese e di una tedesca che ha lo stesso significato, è impossibile che io non sappia che le due parole hanno lo stesso significato; è impossibile che io non riesca a tradurle l'una nell'altra.

Espressioni come «a = a», o derivate da queste, non sono né proposizioni elementari né segni comunque dotati di senso. (Questo si mostrerà più tardi.)

4.25 Se la proposizione elementare è vera, allora lo stato di cose sussiste; se la proposizione elementare è falsa, allora lo stato di cose non sussiste.

4.26 L'enunciazione di tutte le proposizioni elementari vere descrive il mondo completamente. Il mondo è completamente descritto dall'enunciazione di tutte le proposizioni elementari più l'enunciazione di quali tra esse sono vere e quali false.

4.27 Quanto al sussistere o non-sussistere di n stati di cose vi sono [math]\displaystyle{ K_n = \sum_{\nu=0}^n \binom{n}{\nu} }[/math] possibilità.

Ciascuna combinazione di stati di cose può sussistere, le altre non sussistendo.

4.28 A queste combinazioni corrispondono altrettante possibilità della verità – e falsità – di n proposizioni elementari.

[Espandi]4.3 Le possibilità di verità delle proposizioni elementari significano le possibilità del sussistere e non-sussistere degli stati di cose.

4.31 Possiamo presentare le possibilità di verità attraverso schemi fatti nel modo seguente («V» significa «vero», «F» «falso». Le righe delle «V» ed «F» sotto la riga delle proposizioni elementari significano con un simbolismo facilmente comprensibile le loro possibilità di verità):

p	q	r
V	V	V
F	V	V
V	F	V
V	V	F
F	F	V
F	V	F
V	F	F
F	F	F

p	q
V	V
F	V
V	F
F	F

p
V
F

[Espandi]4.4 La proposizione è l'espressione dell'accordo e non-accordo con le possibilità di verità delle proposizioni elementari.

[Espandi]4.41 Le possibilità di verità delle proposizioni elementari sono le condizioni della verità e falsità delle proposizioni.

4.411 Appare subito verosimile che l'introduzione delle proposizioni elementari sia fondamentale per la comprensione di tutti gli altri tipi di proposizione. Già, si percepisce che la comprensione delle proposizioni generali dipende da quella delle proposizioni elementari.

4.42 Quanto all'accordo e non-accordo di una proposizione con le possibilità di verità di n proposizioni elementari, vi sono [math]\displaystyle{ \sum_{\kappa=0}^{K_n} \binom{K_n}{\kappa} = L_n }[/math] possibilità.

[Espandi]4.43 Possiamo esprimere l'accordo con le possibilità di verità assegnando a esse nello schema per esempio il segno «V» (vero).

L'assenza di questo segno significa il non-accordo.

4.431 L'espressione dell'accordo e non-accordo con le possibilità di verità delle proposizioni elementari esprime le condizioni di verità della proposizione.

La proposizione è l'espressione delle sue condizioni di verità.

(Frege aveva quindi perfettamente ragione quando le ha poste in apertura come spiegazione dei segni della sua ideografia. In Frege, tuttavia, è errata la spiegazione del concetto di verità: se «il vero» e «il falso» fossero davvero oggetti e fossero gli argomenti in ~p ecc., allora secondo la determinazione di Frege il senso di «~p» non sarebbe in alcun modo determinato.)

[Espandi]4.44 Il segno che nasce dalla coordinazione di questo segno «V» e delle possibilità di verità è un segno proposizionale.

4.441 È chiaro che al complesso dei segni «F» e «V» non corrisponde alcun oggetto (o complesso di oggetti); no più che alle linee verticali od orizzontali o alle parentesi. – Non vi sono «oggetti logici».

Qualcosa di analogo vale naturalmente per tutti i segni che esprimono lo stesso che gli schemi delle «V» ed «F».

4.442 Per esempio

« 

p	q
V	V	V
F	V	V
V	F
F	F	V

 »

è un segno proposizionale.

(Il «segno di affermazione» di Frege «[math]\displaystyle{ \vdash }[/math]» è logicamente del tutto privo di significato; in Frege (e Russell) esso indica solo che questi autori tengono per vere le proposizioni da esso contrassegnate. «[math]\displaystyle{ \vdash }[/math]» non appartiene quindi alla struttura della proposizione più di quanto [le appartenga] per esempio il numero della proposizione. È impossibile che una proposizione dica di se stessa che è vera.)

Se la sequenza di possibilità di verità nello schema è stabilita una volta per tutte mediante una regola di combinazione, allora l'ultima colonna da sola è già un'espressione delle condizioni di verità. Se riscriviamo questa colonna come riga, il segno proposizionale diviene:

«(VV–V)(p, q)» o, più esplicitamente, «(VVFV)(p, q)».

(Il numero dei posti nella parentesi a sinistra è determinato dal numero dei termini in quella a destra.)

4.45 Per n proposizioni elementari vi sono L_n possibili gruppi di condizioni di verità.

I gruppi di condizioni di verità che appartengono alle possibilità di verità di un certo numero di proposizioni elementari possono essere ordinati in una serie.

[Espandi]4.46 Tra i gruppi possibili di condizioni di verità vi sono due casi estremi.

Nell'un caso la proposizione è vera per tutte le possibilità di verità delle proposizioni elementari. Diciamo che le condizioni di verità sono tautologiche.

Nell'altro caso la proposizione è falsa per tutte le possibilità di verità [delle proposizioni elementari]: le condizioni di verità sono contraddittorie.

Nel primo caso chiamiamo la proposizione una tautologia, nel secondo caso una contraddizione.

[Espandi]4.461 La proposizione mostra che cosa dice; la tautologia e la contraddizione mostrano di non dire niente.

La tautologia non ha condizioni di verità, poiché essa è vera senza condizioni; e la contraddizione non è vera sotto alcuna condizione.

Tautologia e contraddizione sono prive di senso.

(Come il punto dal quale si dipartono due frecce in direzione contraria l'una rispetto all'altra.)

(Ad es. non so nulla del tempo se so che piove o non piove.)

4.4611 La tautologia e la contraddizione non sono però insensate; esse appartengono al simbolismo, similmente in effetti a come lo «0» appartiene al simbolismo dell'aritmetica.

4.462 Tautologia e contraddizione non sono immagini della realtà. Esse non presentano alcuno stato di cose possibile. Quella infatti permette ogni stato di cose possibile, questa nessuno.

Nella tautologia le condizioni dell'accordo con il mondo – le relazioni di presentazione – si annullano a vicenda, in modo tale che essa non sta in alcuna relazione di presentazione con la realtà.

4.463 Le condizioni di verità determinano il gioco che viene lasciato ai fatti dalla proposizione.

(La proposizione, l'immagine, il modello sono, in senso negativo, come un corpo fisso che limita la libertà di movimento di altri [corpi]; in senso positivo, come lo spazio limitato da una sostanza fissa in cui un corpo ha posto.)

La tautologia lascia alla realtà l'intero – infinito – spazio logico; la contraddizione riempie l'intero spazio logico e non lascia alla realtà alcun punto. Nessuna delle due perciò può determinare in alcun modo la realtà.

4.464 La verità della tautologia è certa, della proposizione possibile, della contraddizione impossibile.

(Certo, possibile, impossibile: qui abbiamo l'indicazione di quella gradazione di cui abbiamo bisogno nella teoria della probabilità.)

4.465 Il prodotto logico di una tautologia e di una proposizione dice lo stesso che la proposizione. Quindi tale prodotto è identico alla proposizione. Non si può infatti modificare l'essenziale del simbolo senza modificare il suo senso.

[Espandi]4.466 A un determinato collegamento logico di segni corrisponde un determinato collegamento logico dei loro significati; solo ai segni non collegati corrisponde un qualsiasi collegamento [di significati].

Questo vuol dire che le proposizioni che sono vere per ogni stato di cose non possono assolutamente essere un collegamento di segni, poiché altrimenti potrebbero corrispondere a esse solo collegamenti determinati di oggetti.

(E non vi è alcun collegamento logico a cui non corrisponde alcun collegamento degli oggetti).

Tautologia e contraddizione sono i casi limite del collegamento di segni, cioè ne sono la dissoluzione.

4.4661 Ovviamente anche nella tautologia e nella contraddizione i segni sono collegati tra di loro, cioè sono in relazione gli uni con gli altri, ma queste relazioni sono prive di significato, inessenziali per il simbolo.

[Espandi]4.5 Sembra ora che sia possibile indicare la forma proposizionale più generale: cioè dare una descrizione delle proposizioni di un linguaggio segnico qualunque, in modo tale che ogni senso possibile possa essere espresso mediante un simbolo al quale si attaglia la descrizione, e che ogni simbolo al quale la descrizione si attaglia possa esprimere un senso se i significati dei nomi vengono scelti appropriatamente.

È chiaro che nella descrizione della forma proposizionale più generale può essere descritto solo ciò che essa ha di essenziale – altrimenti infatti essa non sarebbe la più generale.

Che vi sia una forma proposizionale generale è dimostrato dall'impossibilità che vi sia una proposizione la cui forma non si sarebbe potuta prevedere (cioè costruire). La forma generale della proposizione è: le cose stanno così e così.

4.51 Supponiamo che mi fossero date tutte le proposizioni elementari: viene da chiedersi quali proposizioni io potrei costruire con esse. E queste sono tutte le proposizioni ed esse sono così limitate.

4.52 Le proposizioni sono tutto ciò che segue dalla totalità delle proposizioni elementari (e naturalmente anche dall'essere queste la totalità [delle proposizioni elementari]). (Così si potrebbe dire, in un certo senso, che tutte le proposizioni sono generalizzazioni delle proposizioni elementari.)

4.53 La forma proposizionale generale è una variabile.

[Espandi]5 La proposizione è una funzione di verità delle proposizioni elementari.

(La proposizione elementare è una funzione di verità di se stessa.)

5.01 Le proposizioni elementari sono gli argomenti di verità della proposizione.

5.02 Ci vuole poco a confondere gli argomenti delle funzioni con gli indici dei nomi. Infatti riconosco tanto bene dall'argomento come dall'indice il significato del segno che li contiene.

Nel «+_c» di Russell per esempio «c» è un indice che segnala che l'intero segno è il segno dell'addizione per i numeri cardinali. Ma questa simbolizzazione riposa su una convenzione arbitraria e si potrebbe scegliere al posto di «+_c» un segno semplice; in «~p» però «p» non è un indice, ma un argomento: il senso di «~p» non può venir compreso senza che prima sia stato compreso il senso di «p». (Nel nome Giulio Cesare, «Giulio» è un indice. L'indice è sempre una parte di una descrizione dell'oggetto al cui nome lo associamo. Ad es. Il Cesare della gens Iulia.)

La confusione tra argomento e indice è alla base, se non m'inganno, della teoria del significato delle proposizioni e delle funzioni di Frege. Per Frege le proposizioni della logica erano nomi e i loro argomenti gli indici di questi nomi.

[Espandi]5.1 Le funzioni di verità possono essere ordinate in serie.

Questo è il fondamento della teoria della probabilità.

5.101 Le funzioni di verità di un qualunque numero di proposizioni elementari possono essere inserite in uno schema fatto nel modo seguente:

(VVVV)(p, q)	tautologia	(Se p, allora p; e se q, allora q.) (p ⊃ p . q ⊃ q)
(FVVV)(p, q)	a parole:	Non sia p che q. (~(p . q))
(VFVV)(p, q)	»    »	Se q, allora p. (q ⊃ p)
(VVFV)(p, q)	»    »	Se p, allora q. (p ⊃ q)
(VVVF)(p, q)	»    »	p o q. (p ∨ q)
(FFVV)(p, q)	»    »	Non q. ~q
(FVFV)(p, q)	»    »	Non p. ~p
(FVVF)(p, q)	»    »	p o q, ma non sia p che q. (p . ~q : ∨ : q . ~p)
(VFFV)(p, q)	»    »	Se p, allora q; e se q, allora p. (p ≡ q)
(VFVF)(p, q)	»    »	p
(VVFF)(p, q)	»    »	q
(FFFV)(p, q)	»    »	Né p né q. (~p . ~q) o (p | q)
(FFVF)(p, q)	»    »	p e non q. (p . ~q)
(FVFF)(p, q)	»    »	q e non p. (q . ~p)
(VFFF)(p, q)	»    »	q e p. (q . p)
(FFFF)(p, q)	contraddizione	(p e non p; e q e non q.) (p . ~p . q . ~q)

Chiamo fondamenti di verità di una proposizione quelle possibilità di verità degli argomenti di verità della proposizione che la rendono vera.

5.11 Se i fondamenti di verità che sono comuni a un certo numero di proposizioni sono tutti anche fondamenti di verità di una determinata proposizione, allora diciamo che la verità di questa proposizione segue dalla verità di quelle proposizioni.

[Espandi]5.12 In particolare la verità di una proposizione «p» segue dalla verità di un'altra «q» se tutti i fondamenti di verità della seconda sono fondamenti di verità della prima.

5.121 I fondamenti di verità dell'una sono contenuti in quelli dell'altra; p segue da q.

5.122 Se p segue da q, allora il senso di «p» è contenuto nel senso di «q».

5.123 Se un dio crea un mondo in cui certe proposizioni sono vere, allora con ciò crea anche già un mondo in cui tutte le proposizioni che conseguono da esse sono vere. E similmente egli non potrebbe creare un mondo in cui la proposizione «p» è vera senza creare tutti i suoi oggetti.

[Espandi]5.124 La proposizione afferma ogni proposizione che segue da essa.

5.1241 «p . q» è una delle proposizioni che affermano «p» e, allo stesso modo, una delle proposizioni che affermano «q».

Due proposizioni sono contraddittorie quando non vi è alcuna proposizione dotata di senso che le afferma entrambe.

Ogni proposizione che ne contraddice un'altra la nega.

[Espandi]5.13 Che la verità di una proposizione segue dalla verità di altre proposizioni si vede dalla struttura delle proposizioni.

[Espandi]5.131 Se la verità di una proposizione segue dalla verità di altre, questo si esprime attraverso relazioni in cui le forme di quelle proposizioni stanno l'una con l'altra; in effetti non abbiamo bisogno di essere noi a metterle in quelle relazioni collegandole l'una con l'altra in una proposizione; queste relazioni sono bensì interne, sussistono non appena sussistono quelle proposizioni e per il sussistere di quelle proposizioni.

5.1311 Se concludiamo da p ∨ q e ~p a q, qui la relazione delle forme proposizionali di «p ∨ q» e «~p» è nascosta dalla modalità di simbolizzazione. Ma se ad es. scriviamo «p | q . | . p | q» invece che «p ∨ q» e «p | p» (dove p | q = né p né q) anziché «~p», allora la connessione interna diviene evidente.

(Che si possa concludere da (x) . f x a f a mostra che la generalità è presente anche nel simbolo «(x) . f x».)

5.132 Se p segue da q, allora posso concludere da q a p; dedurre p da q.

La modalità dell'inferenza va tratta soltanto dalle due proposizioni.

Solo esse stesse possono giustificare l'inferenza.

«Leggi d'inferenza», intese – come in Frege e Russell – a giustificare le inferenze, sono prive di senso, e sarebbero superflue.

5.133 Ogni deduzione avviene a priori.

5.134 Da una proposizione elementare non è possibile dedurne un'altra.

5.135 In nessun modo si può concludere dal sussistere di un certo stato di cose al sussistere di uno stato di cose del tutto diverso da esso.

[Espandi]5.136 Un nesso di causa che giustifica una tale inferenza non vi è.

5.1361 Non possiamo dedurre gli eventi del futuro da quelli presenti.

La credenza nel nesso di causa è la superstizione.

5.1362 La libertà dell'arbitrio consiste in ciò: che gli atti futuri non possono essere conosciuti adesso. Potremmo conoscerli solo se la causalità fosse una necessità interna, come quella delle inferenze logiche. – La connessione tra il conoscere e ciò che è conosciuto è la connessione della necessità logica.

(«A sa che si verifica p» è privo di senso se p è una tautologia.)

5.1363 Se dal sembrarci una proposizione evidente non segue che essa è vera, allora nemmeno il suo sembrare evidente è una giustificazione per il nostro credere alla sua verità.

[Espandi]5.14 Se una proposizione segue da un'altra, questa dice più di quella, quella meno di questa.

5.141 Se p segue da q e q da p, allora le due sono una e la stessa proposizione.

5.142 La tautologia segue da tutte le proposizioni: essa non dice niente.

5.143 La contraddizione è, tra ciò che le proposizioni hanno in comune, ciò che nessuna proposizione ha in comune con un'altra. La tautologia è ciò che hanno in comune tutte le proposizioni che non hanno niente in comune l'una con l'altra.

La contraddizione scompare per così dire al di fuori di tutte le proposizioni, la tautologia all'interno.

La contraddizione è il limite esterno delle proposizioni, la tautologia il loro centro privo di sostanza.

[Espandi]5.15 Se V_r è il numero dei fondamenti di verità della proposizione «r» e V_rs il numero di quei fondamenti di verità della proposizione «s» che sono ugualmente fondamenti di verità di «r», allora chiamiamo il rapporto V_rs : V_r la misura della probabilità che la proposizione «r» dà alla proposizione «s».

[Espandi]5.151 Sia, in uno schema come quello sopra al n. 5.101, V_r il numero delle «V» nella proposizione r; V_rs il numero di quelle «V» nella proposizione s che si trovano nelle stesse colonne delle «V» della proposizione r. La proposizione r dà allora alla proposizione s la probabilità V_rs : V_r.

5.1511 Non vi è alcun oggetto particolare che sia proprio delle proposizioni della [teoria della] probabilità.

5.152 Chiamiamo indipendenti l'una dall'altra proposizioni che non hanno alcun argomento di verità in comune l'una con l'altra.

Proposizioni indipendenti l'una dall'altra (ad es. due qualsiasi proposizioni elementari) danno l'una all'altra la probabilità ½.

Se p segue da q, la proposizione «q» dà alla proposizione «p» la probabilità 1. La certezza dell'inferenza logica è un caso limite della probabilità.

(Applicazione alla tautologia e alla contraddizione.)

5.153 Una proposizione non è in sé né probabile né improbabile. Un evento capita o non capita, non vi è una via di mezzo.

5.154 In un'urna vi siano altrettante palle bianche e nere (e nessun'altra). Estraggo una palla dopo l'altra e le rimetto di nuovo nell'urna. In tal modo posso stabilire sperimentalmente che i numeri delle palle nere e bianche estratte si avvicinano l'uno all'altro man mano che continuo con le estrazioni.

Quindi questo non è un dato di fatto matematico.

Se ora dico: è altrettanto probabile che io estragga una palla bianca o una nera, questo vuol dire: tutte le circostanze che mi sono note (incluse le leggi naturali assunte ipoteticamente) non danno al capitare dell'un evento più probabilità che al capitare dell'altro. Il che vuol dire che danno a ciascuno – come si comprende facilmente dalle spiegazioni date sopra – la probabilità ½.

Ciò che confermo sperimentalmente è che il capitare dei due eventi è indipendente dalle circostanze, per quanto le conosco.

5.155 L'unità della proposizione della probabilità è: le circostanze – nella misura in cui le conosco – danno al capitare di un determinato evento questo e questo grado di probabilità.

5.156 Quindi la probabilità è una generalizzazione.

Essa comporta una descrizione generale di una forma proposizionale.

Solo in mancanza della certezza usiamo la probabilità. – Se non conosciamo perfettamente un fatto, ma pur sappiamo qualcosa sulla sua forma.

(Una proposizione può essere un'immagine imperfetta di un certo stato di cose, ma è sempre una immagine perfetta.)

La proposizione della probabilità è per così dire un estratto da altre proposizioni.

[Espandi]5.2 Le strutture delle proposizioni stanno in relazioni interne l'una con l'altra.

5.21 Possiamo far emergere queste relazioni interne nel nostro modo di espressione presentando una proposizione come risultato di un'operazione che fa risultare quella proposizione da altre proposizioni (dalle basi dell'operazione).

5.22 L'operazione è l'espressione di una relazione tra le strutture del suo risultato e delle sue basi.

[Espandi]5.23 L'operazione è ciò che deve succedere all'una proposizione per ottenerne l'altra.

5.231 E questo dipenderà naturalmente dalle loro proprietà formali, dalla somiglianza interna delle loro forme.

5.232 La relazione interna che ordina una serie è equivalente all'operazione attraverso la quale un termine risulta dall'altro.

5.233 L'operazione può comparire solo là dove una proposizione risulta in modo logicamente dotato di significato da un'altra. Quindi là dove comincia la costruzione logica della proposizione.

[Espandi]5.234 Le funzioni di verità delle proposizioni elementari sono risultati di operazioni che hanno le proposizioni elementari come basi. (Chiamo queste operazioni operazioni di verità.)

5.2341 Il senso di una funzione di verità di p è una funzione del senso di p.

Negazione, addizione logica, moltiplicazione logica ecc. ecc. sono operazioni.

(La negazione inverte il senso della proposizione.)

[Espandi]5.24 L'operazione si mostra in una variabile; essa mostra come si può passare da una forma di proposizioni a un'altra.

Essa porta a espressione la differenza delle forme.

(E ciò che è in comune tra le basi e il risultato dell'operazione sono appunto le basi.)

5.241 L'operazione non caratterizza alcuna forma, ma solo la differenza delle forme.

5.242 La stessa operazione che ottiene «q» da «p» ottiene da «q» «r» e così di seguito. Questo può esprimersi solo in questo: che «p», «q», «r» sono variabili che portano a espressione generale certe relazioni formali.

[Espandi]5.25 Il comparire dell'operazione non caratterizza il senso della proposizione.

L'operazione in effetti non enuncia niente, solo il proprio risultato, e questo dipende dalle basi dell'operazione.

(Operazione e funzione non possono essere scambiate l'una con l'altra.)

5.251 Una funzione non può essere il proprio stesso argomento, ma il risultato di un'operazione può ben diventare la sua base.

[Espandi]5.252 Solo così è possibile il passaggio da termine a termine in una serie formale (da tipo a tipo nelle gerarchie di Russell e Whitehead). (Russell e Whitehead non hanno ammesso la possibilità di questo passaggio, ma ne hanno più e più volte fatto uso.)

5.2521 Chiamo l'applicazione ripetuta di un'operazione al suo proprio risultato la sua applicazione successiva («O' O' O' a» è il risultato della applicazione successiva, per tre volte, di «O' ξ» ad «a»).

In un senso simile parlo dell'applicazione successiva di più operazioni a un certo numero di proposizioni.

5.2522 Scrivo quindi il termine generale di una serie formale a, O' a, O' O' a, … così: «[a, x, O' x]». Questa espressione tra parentesi è una variabile. Il primo termine dell'espressione tra parentesi è l'inizio della serie formale, il secondo la forma di un termine a piacere x della serie e il terzo la forma di quel termine della serie che segue immediatamente x.

5.2523 Il concetto dell'applicazione successiva dell'operazione è equivalente al concetto «e così via».

5.253 Un'operazione può annullare l'effetto di un'altra. Le operazioni possono cancellarsi l'un l'altra.

5.254 L'operazione può scomparire (ad es. la negazione in «~~p», ~~p = p).

[Espandi]5.3 Tutte le proposizioni sono risultati di operazioni di verità con le proposizioni elementari.

L'operazione di verità è il modo in cui dalle proposizioni elementari risulta la funzione di verità.

Secondo l'essenza dell'operazione di verità, allo stesso modo in cui dalle proposizioni elementari risulta la loro funzione di verità, dalle funzioni di verità risulta una nuova funzione di verità. Ogni operazione di verità genera, da funzioni di verità di proposizioni elementari, di nuovo una funzione di verità di proposizioni elementari, una proposizione. Il risultato di ogni operazione di verità con i risultati di operazioni di verità con proposizioni elementari è di nuovo il risultato di una operazione di verità con proposizioni elementari.

Ogni proposizione è il risultato di operazioni di verità con proposizioni elementari.

5.31 Gli schemi al n. 4.31 hanno quindi un significato anche se «p», «q», «r», ecc. non sono proposizioni elementari.

Ed è facile vedere che il segno proposizionale al n. 4.442 esprime una funzione di verità di proposizioni elementari anche se «p» e «q» sono funzioni di verità di proposizioni elementari.

5.32 Tutte le funzioni di verità sono risultati dell'applicazione successiva di un numero finito di operazioni di verità alle proposizioni elementari.

[Espandi]5.4 Qui si mostra che non vi sono «oggetti logici», «costanti logiche» (nel senso di Frege e di Russell).

5.41 Infatti tutti i risultati di operazioni di verità con funzioni di verità che sono una e la stessa funzione di verità di proposizioni elementari sono identici.

5.42 È evidente che ∨, ⊃, ecc. non sono relazioni nel senso di destra e sinistra ecc.

La possibilità di definire i «segni primitivi» logici di Frege e di Russell l'uno con riferimento all'altro mostra già che questi non sono segni primitivi e, a maggior ragione, che essi non designano alcuna relazione.

Ed è evidente che il «⊃» che noi definiamo mediante «~» e «∨» è identico a quello mediante il quale e mediante «~» definiamo «∨»; e che questo «∨» è identico al primo. E così via.

5.43 Che da un fatto p debbano seguirne infiniti altri, cioè ~~p, ~~~~p, ecc., è, già a prima vista, difficile a credersi. E non è meno degno di nota che le infinite proposizioni della logica (della matematica) seguano da una mezza dozzina di «leggi fondamentali».

Ma tutte le proposizioni della logica dicono lo stesso – cioè niente.

[Espandi]5.44 Le funzioni di verità non sono funzioni materiali.

Se ad es. si può generare un'affermazione mediante una doppia negazione, allora la negazione è – in qualche senso – contenuta nell'affermazione? «~~p» nega ~p o afferma p? O fa entrambe le cose?

La proposizione «~~p» non tratta della negazione come di un oggetto; ma la possibilità della negazione è già implicata nell'affermazione.

E se vi fosse un oggetto chiamato «~», «~~p» dovrebbe dire qualcosa di diverso da «p». Poiché l'una proposizione tratterebbe appunto di ~, l'altra no.

5.441 Questo scomparire delle costanti logiche apparenti entra in scena anche nel momento in cui «(∃x) . ~f x» dice lo stesso che «(x) . f x», o «(∃x) . f x . x = a» lo stesso che «f a».

5.442 Se ci è data una proposizione, con essa ci sono già dati anche i risultati di tutte le operazioni di verità che hanno quella proposizione come base.

[Espandi]5.45 Se vi sono segni logici primitivi, una logica corretta deve render chiara la loro posizione reciproca e giustificare la loro esistenza. Deve divenire chiara la costruzione della logica a partire dai suoi segni primitivi.

5.451 Se la logica ha concetti fondamentali, essi devono essere indipendenti gli uni dagli altri. Se viene introdotto un concetto fondamentale, esso dev'essere introdotto in tutte le connessioni in cui compare. Non si può quindi introdurlo dapprima per una connessione, poi di nuovo per un'altra. Ad es.: una volta introdotta la negazione, dobbiamo comprenderla tanto in proposizioni della forma «~p» quanto in proposizioni come «~(p ∨ q)», «(∃x) . ~f x ecc. Non possiamo introdurla prima per l'una classe di casi, poi per l'altra, poiché allora rimarrebbe dubbio se il suo significato sia lo stesso nei due casi e non vi sarebbe alcun motivo per usare nei due casi la stessa modalità di connessione dei segni.

(In breve, per l'introduzione dei segni primitivi vale, mutatis mutandis, lo stesso che Frege (nei Grundgesetze der Arithmetik) ha detto per l'introduzione di segni mediante definizioni.)

5.452 L'introduzione di un nuovo espediente nel simbolismo della logica deve sempre essere un evento gravido di conseguenze. Nessun nuovo espediente può essere introdotto nella logica – per così dire, con aria del tutto innocente – tra parentesi o a margine.

(Così nei Principia Mathematica di Russell e Whitehead compaiono definizioni e leggi fondamentali espresse a parole. Perché qui improvvisamente parole? Questo richiederebbe una giustificazione. Essa manca e deve mancare; poiché il procedimento, di fatto, non è consentito.)

Se però l'introduzione di un nuovo espediente in una certa posizione si è dimostrata necessaria, ci si deve subito chiedere: dove, allora, questo espediente dev'essere sempre applicato? Adesso bisogna spiegare la sua posizione nella logica.

5.453 Tutti i numeri della logica devono poter essere giustificati.

O piuttosto: deve rendersi chiaro che nella logica non vi sono numeri.

Non vi sono numeri speciali.

[Espandi]5.454 Nella logica non vi è alcuna giustapposizione, non può esservi alcuna classificazione.

Nella logica non può esservi niente di più generale o di più particolare.

5.4541 Le soluzioni dei problemi logici devono essere semplici, poiché esse stabiliscono lo standard della semplicità.

Gli uomini hanno sempre avuto il sentimento che debba esservi un ambito di domande le cui risposte sono – a priori – unite simmetricamente, secondo una struttura chiusa e regolare.

Un ambito nel quale vale la sentenza: simplex sigillum veri.

[Espandi]5.46 Se si introducessero i segni logici correttamente, si sarebbe già introdotto con ciò anche il senso di tutte le loro combinazioni; quindi non solo «p ∨ q», ma anche «~(p ∨ ~q)» ecc. ecc. Si sarebbe già introdotto con ciò anche l'effetto di tutte le possibili combinazioni di parentesi. E con ciò sarebbe divenuto chiaro che i veri e propri segni primitivi generali non sono i «p ∨ q», «(∃x) . f x» ecc., bensì la forma più generale delle loro combinazioni.

[Espandi]5.461 È significativo il fatto apparentemente irrilevante che le pseudo-relazioni logiche, come ∨ e ⊃, hanno bisogno delle parentesi – al contrario delle relazioni reali.

L'uso delle parentesi con questi segni primitivi apparenti indica già che questi non sono i segni primitivi reali. E certo nessuno crederà che le parentesi abbiano un significato autonomo.

5.4611 I segni logici di operazione sono punteggiatura.

[Espandi]5.47 È chiaro che ciò che può essere detto fin dal principio sulla forma di tutte le proposizioni deve poter essere detto tutto in una volta.

Nella proposizione elementare sono già contenute tutte le operazioni logiche. Poiché «f a» dice lo stesso che «(∃x) . f x . x = a».

Dov'è composizione sono anche argomento e funzione, e dove sono questi sono già tutte le costanti logiche.

Si potrebbe dire: l'unica costante logica è ciò che tutte le proposizioni, per loro natura, hanno in comune l'una con l'altra.

Ma questa è la forma generale della proposizione.

[Espandi]5.471 La forma generale della proposizione è l'essenza della proposizione.

5.4711 Indicare l'essenza della proposizione vuol dire indicare l'essenza di ogni descrizione, e quindi l'essenza del mondo.

5.472 La descrizione della forma più generale della proposizione è la descrizione dell'uno e unico segno primitivo generale della logica.

[Espandi]5.473 La logica deve badare a se stessa.

Un segno possibile deve anche poter designare. Tutto ciò che nella logica è possibile è anche lecito. («Socrate è identico» non vuol dire niente perché non vi è alcuna proprietà che si chiama «identico». La proposizione è insensata perché non abbiamo stabilito una determinazione arbitraria, ma non perché il simbolo sarebbe illegittimo in sé e per sé.)

In un certo senso, nella logica non possiamo sbagliarci.

5.4731 L'autoevidenza di cui Russell ha parlato tanto può diventare superflua in logica solo nella misura in cui il linguaggio stesso impedisce ogni errore logico. – L'essere la logica a priori consiste nell'essere impossibile pensare illogicamente.

[Espandi]5.4732 Non possiamo dare a un segno il senso sbagliato.

5.47321 Il rasoio di Occam non è naturalmente una regola arbitraria o giustificata dal suo successo pratico: esso dice che unità segniche non necessarie non significano niente.

Segni che realizzano uno scopo sono logicamente equivalenti; segni che non realizzano alcuno scopo sono logicamente privi di significato.

5.4733 Frege dice: ogni proposizione costruita legittimamente deve avere un senso; e io dico: ogni proposizione possibile è costruita legittimamente, e se non ha senso ciò può dipendere solo dal non aver noi dato alcun significato a qualcuno dei suoi elementi costitutivi.

(Anche se crediamo di averlo fatto.)

Quindi «Socrate è identico» non dice niente perché alla parola «identico» non abbiamo dato alcun significato come aggettivo. Infatti, quando funziona come segno d'identità, questa parola simbolizza in modo del tutto diverso – la relazione di designazione è un'altra – così che anche il simbolo è del tutto diverso nei due casi; i due simboli hanno in comune solo il segno, per caso.

5.474 Il numero delle operazioni fondamentali necessarie dipende solo dalla nostra notazione.

5.475 È solo questione di costruire un sistema di segni con un determinato numero di dimensioni – con una determinata molteplicità matematica.

5.476 È chiaro che qui non si tratta di un novero di concetti fondamentali che devono essere designati, ma dell'espressione di una regola.

[Espandi]5.5 Ogni funzione di verità è un risultato dell'applicazione successiva dell'operazione (– – – – –V)(ξ, ....) a proposizioni elementari.

Questa operazione nega tutte le proposizioni nella parentesi di destra e io la chiamo la negazione di queste proposizioni.

5.501 Indico un'espressione tra parentesi i cui termini sono proposizioni – se l'ordine dei termini nella parentesi è indifferente – mediante un segno della forma «[math]\displaystyle{ ( \bar{\xi} ) }[/math]». «ξ» è una variabile i cui valori sono i termini dell'espressione tra parentesi; e la linea sopra la variabile indica che essa sta per tutti i suoi valori nella parentesi.

(Se quindi, per esempio, ξ ha i 3 valori P, Q, R, allora [math]\displaystyle{ ( \bar{\xi} ) }[/math] = (P, Q, R).)

I valori delle variabili si stabiliscono.

Il fatto di stabilirli consiste nel descrivere le proposizioni per cui sta la variabile.

Come avvenga la descrizione dei termini dell'espressione tra parentesi è inessenziale.

Noi possiamo distinguere tre modalità della descrizione: 1. L'enumerazione diretta. In questo caso possiamo semplicemente inserire al posto della variabile i suoi valori costanti. 2. L'enunciazione di una funzione f x i cui valori sono, per tutti i valori di x, le proposizioni da descrivere. 3. L'enunciazione di una legge formale secondo la quale quelle proposizioni sono costruite. In questo caso i termini dell'espressione tra parentesi sono tutti i termini di una serie formale.

5.502 Scrivo dunque, anziché «(– – – – –V)(ξ, ....)», «[math]\displaystyle{ N ( \bar{\xi} ) }[/math]».

[math]\displaystyle{ N ( \bar{\xi} ) }[/math] è la negazione di tutti i valori della variabile proposizionale ξ.

5.503 È evidentemente agevole esprimere come con questa operazione possono essere costruite proposizioni e come proposizioni non vanno costruite con essa; anche questo perciò deve poter trovare un'espressione esatta.

[Espandi]5.51 Se ξ ha solo un valore, allora [math]\displaystyle{ N ( \bar{\xi} ) }[/math] = ~p (non p); se ha due valori, allora [math]\displaystyle{ N ( \bar{\xi} ) }[/math] = ~p . ~q (né p né q).

5.511 Come può la logica, onnicomprensiva, specchio del mondo, impiegare cavilli e manipolazioni così particolari? Solo in quanto questi si legano tutti a una rete infinitamente sottile, al grande specchio.

5.512 «~p» è vera se è falsa «p». Quindi nella proposizione vera «~p», «p» è una proposizione falsa. Ora come può il tratto «~» portarla a concordare con la realtà?

Quello che in «~p» nega non è però il «~», bensì ciò che è comune a tutti i segni di questa notazione che negano p.

Cioè la regola comune secondo la quale «~p», «~~~p», «~p ∨ ~p», «~p . ~p», ecc. ecc. (ad infinitum) vengono costruite. E questo qualcosa che è comune [a tutti i segni che negano p] rispecchia la negazione.

5.513 Si potrebbe dire: ciò che è comune a tutti i simboli che affermano tanto p quanto q è la proposizione «p . q». Ciò che è comune a tutti i simboli che affermano p oppure q è la proposizione «p ∨ q».

E così si può dire: due proposizioni sono contraddittorie se non hanno niente in comune, e: ogni proposizione ha solo un negativo, poiché vi è una sola proposizione che si trova del tutto al di fuori di essa.

Si mostra così anche nella notazione di Russell che «q : p ∨ ~p» dice lo stesso che «q»; che «p ∨ ~p» non dice niente.

5.514 Se è stabilita una notazione, allora vi è in essa una regola secondo la quale vengono costruite tutte le proposizioni che negano p, una regola secondo la quale vengono costruite tutte le proposizioni che affermano p, una regola secondo la quale vengono costruite tutte le proposizioni che affermano p o q, e così di seguito. Queste regole sono equivalenti ai simboli e in essi si rispecchia il loro senso.

[Espandi]5.515 Deve mostrarsi nei nostri simboli che ciò che è collegato da «∨», «.», ecc. devono essere proposizioni.

Ed è così, poiché il simbolo «p» e «q» presuppone esso stesso «∨», «~» ecc. Se il segno «p» in «p ∨ q» non sta per un segno complesso, allora esso, da solo, non può avere senso; allora però non possono avere senso nemmeno i segni che hanno lo stesso senso di p, come «p ∨ p», «p . p» ecc. Se tuttavia «p ∨ p» non ha senso, allora neanche «p ∨ q» può avere senso.

5.5151 Il segno della proposizione negativa dev'essere costruito con il segno della positiva? Perché non si dovrebbe poter esprimere una proposizione negativa attraverso un fatto negativo? (Per esempio: se «a» non sta in una determinata relazione con «b», questo potrebbe esprimere che a R b non si verifica.)

Ma anche qui la proposizione negativa è indirettamente costruita attraverso la positiva.

La proposizione positiva deve presupporre l'esistenza della proposizione negativa e viceversa.

[Espandi]5.52 Se i valori di ξ sono tutti i valori di una funzione f x per tutti i valori di x, allora sarà [math]\displaystyle{ N ( \bar{\xi} ) }[/math] = ~(∃x) . f x.

5.521 Io separo il concetto tutti dalla funzione di verità.

Frege e Russell hanno introdotto la generalità in connessione con il prodotto logico o con la somma logica. Così [però] diveniva difficile comprendere le proposizioni (∃x) . f x e (x) . f x, contenute nelle quali vi sono entrambe le idee.

5.522 Caratteristico della designazione della generalità è in primo luogo che essa rimanda a un archetipo logico; e in secondo luogo che essa mette in evidenza le costanti.

5.523 La designazione della generalità compare come argomento.

5.524 Quando gli oggetti sono dati, ci sono anche già dati con ciò tutti gli oggetti.

Quando le proposizioni elementari sono date, sono anche date con ciò tutte le proposizioni elementari.

5.525 È scorretto rendere in parole la proposizione «(∃x) . f x» con «f x è possibile» – come fa Russell.

Certezza, possibilità o impossibilità di uno stato di cose non sono espresse da una proposizione, ma dal fatto che un'espressione sia una tautologia, una proposizione dotata di senso o una contraddizione.

Quel precedente al quale ci si vorrebbe sempre richiamare deve trovarsi già nel simbolo stesso.

[Espandi]5.526 Si può descrivere completamente il mondo mediante proposizioni perfettamente generalizzate, cioè senza assegnare preventivamente alcun nome a un determinato oggetto.

Per venire quindi al modo abituale di espressione, dopo un'espressione «vi è uno e un solo x che…» si deve dire semplicemente: e questo x è a.

5.5261 Una proposizione perfettamente generalizzata è composita, come ogni altra proposizione. (Questo si mostra nel fatto che dobbiamo menzionare «φ» e «x» separatamente in «(∃x, φ) . φ x». Entrambi [i simboli, «φ» e «x»,] stanno indipendentemente in relazioni di designazione col mondo, come nella proposizione non generalizzata.)

Segno di riconoscimento del simbolo composito: esso ha qualcosa in comune con altri simboli.

5.5262 La verità o falsità di ogni proposizione cambia qualcosa nella costruzione generale del mondo. E il gioco che viene lasciato alla sua costruzione dalla totalità delle proposizioni elementari è proprio quello che delimitano le proposizioni completamente generali.

(Se una proposizione elementare è vera, con ciò è comunque vera una proposizione elementare in più.)

[Espandi]5.53 Esprimo l'uguaglianza dell'oggetto mediante l'uguaglianza del segno, e non con l'aiuto di un segno di uguaglianza. [Ed esprimo] la diversità degli oggetti mediante la diversità dei segni.

5.5301 È ovvio che l'identità non è una relazione tra oggetti. Ciò risulta molto chiaro se si esamina ad es. la proposizione «(x) : f x . ⊃ . x = a». Ciò che dice questa proposizione è semplicemente che solo a soddisfa la funzione f, e non che soddisfano la funzione f solo quelle cose che hanno una certa relazione con a.

Certo si potrebbe allora dire che proprio solo a ha questa relazione con a, ma per esprimere ciò avremmo bisogno appunto del segno di uguaglianza.

5.5302 La definizione di «=» di Russell non è adeguata; perché in accordo con essa non si può dire che due oggetti hanno in comune tutte le loro proprietà. (Anche se questa proposizione non è mai corretta, essa ha pur senso.)

5.5303 Detto incidentalmente: il dire di due cose che sono identiche è un nonsenso, e il dire di una che è identica a se stessa non dice proprio niente.

5.531 Non scrivo dunque «f (a, b) . a = b», ma «f (a, a)» (o «f (b, b)»). E non «f (a, b) . ~a = b», ma «f (a, b)».

[Espandi]5.532 E analogamente: non «(∃x, y) . f (x, y) . x = y», ma «(∃x) . f (x, x)»; e non «(∃x, y) . f (x, y) . ~x = y», ma «(∃x, y) . f (x, y)».

(Quindi, in luogo del russelliano «(∃x, y) . f x, y)»: «(∃x, y) . f (x, y) . ∨ . (∃x) . f x, x)».)

5.5321 Anziché «(x) : f x ⊃ x = a» scriviamo quindi ad es. «(∃x) . f x. ⊃ .f a : ~(∃x, y) . f x . f y».

E la proposizione «un solo x soddisfa f ( )» suona: «(∃x) . f x : ~(∃x, y) . f x . f y».

5.533 Il segno di uguaglianza dunque non è una parte costitutiva essenziale dell'ideografia.

5.534 E ora vediamo che pseudo-proposizioni come «a = a», «a = b . b = c. ⊃ a = c», «(x) . x = x», «(∃x) . x = a», ecc. in un'ideografia corretta non possono essere scritte affatto.

[Espandi]5.535 Con ciò si risolvono anche tutti i problemi che erano collegati a queste pseudo-proposizioni.

Tutti i problemi che porta con sé l'«axiom of infinity» di Russell possono essere risolti già qui.

Ciò che l'axiom of infinity intende dire si esprimerebbe nel linguaggio con l'esservi infiniti nomi con significati diversi.

5.5351 Vi sono certi casi in cui sì è tentati di usare espressioni della forma «a = a» o «p ⊃ p» e simili. In effetti ciò è evidente quando si vorrebbe parlare dell'archetipo: proposizione, cosa, ecc. Così nei Principles of Mathematics Russell ha reso in simboli, mediante p ⊃ p, il nonsenso «p è una proposizione», e lo ha premesso come ipotesi a certe proposizioni in modo che i loro posti per l'argomento potessero essere riempiti solo da proposizioni.

(A questo proposito è già nonsenso premettere l'ipotesi p ⊃ p a una proposizione per assicurarle argomenti della forma giusta, poiché l'ipotesi, per un argomento che non sia una proposizione, diventa non falsa, ma insensata, e poiché la proposizione stessa con il genere sbagliato di argomenti diventa insensata, cosicché essa stessa garantisce contro gli argomenti illegittimi tanto bene, o tanto male, quanto l'ipotesi priva di senso aggiunta a questo scopo.)

5.5352 Similmente si voleva esprimere «non vi sono cose» mediante «~(∃x) . x = x». Ma quand'anche questa fosse una proposizione – non sarebbe vera anche se «vi fossero cose» ma non fossero identiche a se stesse?

[Espandi]5.54 Nella forma generale della proposizione, la proposizione compare nella proposizione solo come base delle operazioni di verità.

5.541 A un primo sguardo sembra che una proposizione potrebbe comparire in un'altra anche in modo diverso.

Soprattutto in certe forme proposizionali della psicologia, come «A crede che si verifichi p», o «A pensa p», ecc.

Qui infatti, guardando superficialmente, sembra che la proposizione p stia in una sorta di relazione con un oggetto A.

(E nella moderna teoria della conoscenza (Russell, Moore, ecc.) queste proposizioni sono state in effetti intese così.)

[Espandi]5.542 È tuttavia chiaro che «A crede che p», «A pensa p», «A dice p» sono della forma «“p” dice p»: e qui non si tratta di un'associazione di un fatto e di un oggetto, ma di un'associazione di fatti mediante associazione dei loro oggetti.

5.5421 Ciò mostra anche che, come essa viene intesa nella superficiale psicologia di oggi, l'anima – il soggetto, ecc. – è un'assurdità.

Un'anima composita non sarebbe infatti più un'anima.

5.5422 La spiegazione corretta della forma della proposizione «A esprime il giudizio p» deve mostrare che è impossibile esprimere un giudizio insensato. (La teoria di Russell non soddisfa questo requisito.)

5.5423 Percepire un complesso vuol dire percepire che le sue parti costitutive stanno in relazione le une con le altre in questo e questo modo.

Questo spiega bene anche come la figura

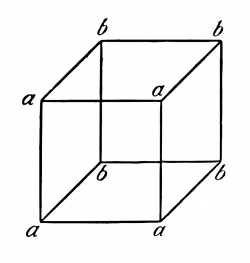
possa essere vista come cubo in due modi; e [spiega bene anche] tutti i fenomeni simili. Poiché vediamo davvero due fatti diversi.

(Se bado prima ai vertici a e solo di sfuggita ai b, gli a appaiono davanti; e viceversa.)

[Espandi]5.55 Dobbiamo ora rispondere a priori alla domanda circa tutte le possibili forme delle proposizioni elementari.

La proposizione elementare consiste di nomi. Poiché tuttavia non possiamo indicare il numero dei nomi con significato diverso, non possiamo indicare neanche la composizione della proposizione elementare.

5.551 Nostro principio è che ogni domanda che può essere decisa dalla logica deve poter essere decisa senza ricorrere ad altro.

(E se ci ritroviamo nella situazione di dover rispondere a una tale questione guardando al mondo, ciò mostra che siamo su una strada radicalmente sbagliata.)

[Espandi]5.552 L'«esperienza» di cui abbiamo bisogno per la comprensione della logica non è l'esperienza che qualcosa sta così e così, bensì che qualcosa è: ma ciò appunto non è esperienza.

La logica è prima di ogni esperienza – che qualcosa è così. Essa è prima del come, non prima del cosa.

5.5521 E se fosse altrimenti, come potremmo applicare la logica? Si potrebbe dire: se una logica vi fosse anche se non vi fosse un mondo, allora come potrebbe esservi una logica essendovi un mondo?

5.553 Russell sosteneva che vi fossero relazioni semplici tra diversi numeri di cose (individuals). Ma tra quali numeri? E come lo si dovrebbe decidere? – Attraverso l'esperienza?

(Non vi è un numero speciale.)

[Espandi]5.554 L'enumerazione di ogni forma particolare sarebbe completamente arbitraria.

5.5541 Dovrebbe poter essere indicato a priori se è possibile che io mi trovi ad es. nella situazione di dover simbolizzare qualcosa con il segno di una relazione a 27 posti.

5.5542 Ma allora ci è davvero lecito chiederlo? Possiamo costituire una forma segnica e non sapere se a essa possa corrispondere qualcosa?

Ha un senso chiedere cosa deve essere affinché qualcosa possa verificarsi?

5.555 È chiaro che abbiamo un concetto della proposizione elementare a prescindere dalla sua particolare forma logica.

Dove però si possono formare simboli secondo un sistema, lì ciò che è logicamente importante è questo sistema, e non i singoli simboli.

E come sarebbe possibile che io nella logica avessi a che fare con forme che posso inventare? Al contrario devo avere a che fare con ciò che mi rende possibile inventarle.

[Espandi]5.556 Non può esservi una gerarchia delle forme delle proposizioni elementari. Possiamo prevedere solo ciò che costruiamo noi stessi.

5.5561 La realtà empirica è limitata dalla totalità degli oggetti. Il limite si mostra ancora nella totalità delle proposizioni elementari.

Le gerarchie sono e devono essere indipendenti dalla realtà.

5.5562 Se sappiamo per ragioni puramente logiche che devono esservi proposizioni elementari, allora deve saperlo chiunque comprenda le proposizioni nella loro forma non analizzata.

5.5563 Tutte le proposizioni del nostro linguaggio comune sono in effetti, così come sono, logicamente del tutto in ordine. – Ciò di semplicissimo che qui dobbiamo indicare non è un simulacro della verità, ma la piena verità stessa.

(I nostri problemi non sono astratti, bensì forse i più concreti che vi siano.)

[Espandi]5.557 L'applicazione della logica decide di quali proposizioni elementari vi sono.

Ciò che si trova nell'applicazione non può essere anticipato dalla logica.

Questo è chiaro: la logica non può collidere con la sua applicazione.

Ma la logica e la sua applicazione devono toccarsi.

Quindi la logica e la sua applicazione non possono sovrapporsi l'una all'altra.

5.5571 Se non posso indicare a priori le proposizioni elementari, volerle indicare deve condurre a un palese nonsenso.

[Espandi]5.6 I limiti del mio linguaggio significano i limiti del mio mondo.

5.61 La logica riempie il mondo; i limiti del mondo sono anche i suoi limiti.

Dunque nella logica non possiamo dire: nel mondo vi è questo e questo, quello no.

Apparentemente, infatti, ciò presupporrebbe che noi escludessimo certe possibilità, e questo non può verificarsi, poiché altrimenti la logica dovrebbe uscire dai limiti del mondo; se essa cioè potesse considerare questi limiti anche dall'altro lato.

Non possiamo pensare ciò che non possiamo pensare; quindi non possiamo nemmeno dire ciò che non possiamo pensare.

[Espandi]5.62 Questa osservazione dà la chiave per rispondere alla domanda fino a che punto il solipsismo sia una verità.

Ciò, infatti, che il solipsismo intende è del tutto corretto; solo non può essere detto, ma si mostra.

Che il mondo è il mio mondo si mostra nel significare i limiti del linguaggio (del solo linguaggio che io comprendo) i limiti del mio mondo.

5.621 Il mondo e la vita sono uno.

[Espandi]5.63 Io sono il mio mondo. (Il microcosmo.)

5.631 Il soggetto che pensa, che si fa rappresentazioni, non vi è. Se scrivessi un libro intitolato Il mondo come io l'ho trovato, in esso dovrei raccontare anche del mio corpo e dire quali membra sottostanno alla mia volontà e quali no, ecc.; questo è quindi un metodo per isolare il soggetto, o meglio per mostrare che in un senso importante non vi è alcun soggetto: di esso solo, infatti, in questo libro non si potrebbe parlare. –

5.632 Il soggetto non appartiene al mondo, bensì è un limite del mondo.

[Espandi]5.633 Dove nel mondo si può riscontrare un soggetto metafisico? Tu dici che qui tutto sta come con l'occhio e il campo visivo. Ma l'occhio in realtà non lo vedi.

E niente nel campo visivo permette di concludere che esso viene visto da un occhio.

5.6331 Il campo visivo, cioè, non ha una forma come questa:

5.634 Ciò è connesso con il fatto che nessuna parte della nostra esperienza è al contempo a priori.

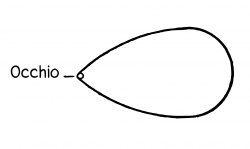
Tutto ciò che vediamo potrebbe anche essere altrimenti.

Tutto ciò che possiamo affatto descrivere potrebbe anche essere altrimenti.

Non vi è alcun ordine a priori delle cose.

[Espandi]5.64 Qui si vede che il solipsismo, portato avanti rigorosamente, coincide con il puro realismo. L'Io del solipsismo si raggrinzisce in un punto privo di estensione, e rimane la realtà a esso coordinata.

5.641 Vi è dunque davvero un senso in cui nella filosofia si può parlare dell'Io in modo non psicologico.

L'Io entra nella filosofia con questo: che «il mondo è il mio mondo».

L'Io filosofico non è l'uomo, non è il corpo umano o l'anima umana di cui tratta la psicologia, bensì il soggetto metafisico, non una parte del mondo, ma il suo limite.

[Espandi]6 La forma generale della funzione di verità è: [math]\displaystyle{ [ \bar{p}, \bar{\xi}, N (\bar{\xi}) ] }[/math].

Questa è la forma generale della proposizione.

6.001 Questo non dice altro se non che ogni proposizione è un risultato dell'applicazione successiva dell'operazione [math]\displaystyle{ N (\bar{\xi}) }[/math] alle proposizioni elementari.

6.002 Se è data la forma generale secondo cui è costruita una proposizione, è anche già data con ciò la forma generale secondo cui da una proposizione, mediante un'operazione, può esserne generata un'altra.

6.01 La forma generale dell'operazione [math]\displaystyle{ \Omega ' (\bar{\eta}) }[/math] è quindi: [math]\displaystyle{ [\bar{\xi}, N(\bar{\xi})]' (\bar{\eta}) (= [ \bar{\eta}, \bar{\xi}, N (\bar{\xi}) ]) }[/math].

Questa è la forma più generale del passaggio da una proposizione a un'altra.

[Espandi]6.02 E così veniamo ai numeri: definisco

[math]\displaystyle{ x = \Omega^{0 \prime} x \text{ Def.} }[/math] e
[math]\displaystyle{ \Omega^{\prime} \Omega^{ \nu \prime} x = \Omega^{ \nu + 1 \prime} x \text{ Def.} }[/math]

Secondo questa regola segnica quindi scriviamo la serie [math]\displaystyle{ x, \Omega ' x, \Omega ' \Omega ' x, \Omega ' \Omega ' \Omega ' x, ..... }[/math]

così: [math]\displaystyle{ \Omega^{0 \prime} x, \Omega^{0+1 \prime} x, \Omega^{0 + 1 + 1 \prime} x, \Omega^{0 + 1 + 1 + 1 \prime} x, ..... }[/math]

Dunque, invece che «[math]\displaystyle{ [ x, \xi, \Omega ' \xi ] }[/math]», scrivo:

«[math]\displaystyle{ [ \Omega^{0 \prime} x, \Omega^{ \nu \prime} x, \Omega^{ \nu + 1 \prime} x ] }[/math]».

E definisco:

[math]\displaystyle{ 0 + 1 = 1 \text{ Def.} }[/math]

[math]\displaystyle{ 0 + 1 + 1 = 2 \text{ Def.} }[/math]

[math]\displaystyle{ 0 + 1 + 1 + 1 = 3 \text{ Def.} }[/math]

(e così di seguito).

6.021 Il numero è l'esponente di un'operazione.

6.022 Il concetto di numero non è altro che ciò che hanno in comune tutti i numeri, la forma generale del numero.

Il concetto di numero è il numero variabile.

E il concetto dell'uguaglianza di numeri è la forma generale di tutte le particolari uguaglianze di numeri.

[Espandi]6.03 La forma generale del numero intero è: [0, ξ, ξ + 1].

6.031 La teoria delle classi è, nella matematica, del tutto superflua.

Questo è connesso col fatto che la generalità di cui abbiamo bisogno nella matematica non è la generalità casuale.

[Espandi]6.1 Le proposizioni della logica sono tautologie.

[Espandi]6.11 Le proposizioni della logica, dunque, non dicono niente. (Esse sono le proposizioni analitiche.)

6.111 Teorie che fanno sembrare dotata di contenuto una proposizione della logica sono sempre false. Si potrebbe ad es. credere che le parole «vero» e «falso» designino due proprietà tra altre proprietà, e di conseguenza sembrerebbe un fatto degno di nota che ogni proposizione possieda una di queste [due] proprietà. Ciò apparirebbe tutto tranne che ovvio, non più ovvio di quanto per esempio suonerebbe la proposizione «tutte le rose sono o gialle o rosse», anche se essa fosse vera. Già, quella proposizione [logica] riceve tutto il carattere di una proposizione delle scienze naturali, e questa è l'indicazione sicura che è stata intesa in modo errato.

6.112 La spiegazione corretta delle proposizioni logiche deve dar loro una posizione unica tra tutte le proposizioni.

6.113 Che si possa riconoscere che sono vere dal solo simbolo è il carattere specifico delle proposizioni logiche, e questo fatto racchiude in sé tutta la filosofia della logica. E così un altro dei fatti più importanti è che la verità o falsità delle proposizioni non logiche non si possa riconoscere dalla sola proposizione.

[Espandi]6.12 Che le proposizioni della logica siano tautologie mostra le proprietà formali – logiche – del linguaggio, del mondo.

Che le loro parti costitutive così legate diano una tautologia caratterizza la logica delle loro parti costitutive.

Affinché proposizioni legate in modo determinato diano una tautologia, esse devono avere determinate proprietà della struttura. Che esse così collegate diano una tautologia mostra quindi che esse possiedono queste proprietà della struttura.

6.1201 Che ad es. le proposizioni «p» e «~p», nel collegamento «~(p . ~p)», diano una tautologia mostra che esse si contraddicono l'un l'altra. Che le proposizioni «p ⊃ q», «p» e «q», collegate tra di loro nella forma «(p ⊃ q) . (p) : ⊃ : (q)», diano una tautologia mostra che q segue da p e p ⊃ q. Che «(x) . f x : ⊃ : f a» sia una tautologia [mostra] che f a segue da (x) . f x, ecc. ecc.

6.1202 È chiaro che per lo stesso scopo si potrebbero impiegare, anziché le tautologie, anche le contraddizioni.

6.1203 Per riconoscere una tautologia come tale, nei casi in cui nella tautologia non compare alcuna designazione di generalità ci si può servire del seguente metodo grafico: scrivo anziché «p», «q», «r» ecc. «V p F», «V q F», «V r F» ecc. Esprimo le combinazioni di verità mediante parentesi, ad es.:

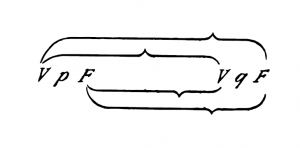
ed esprimo la correlazione tra la verità o falsità dell'intera proposizione e le combinazioni di verità degli argomenti di verità mediante linee nel modo seguente:

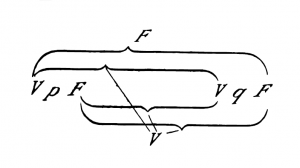
Questo segno presenterebbe dunque ad es. la proposizione p ⊃ q. Ora voglio ad es. controllare se la proposizione ~(p . ~p) (principio di non contraddizione) è una tautologia. La forma «~ ξ» viene scritta, nella nostra notazione,

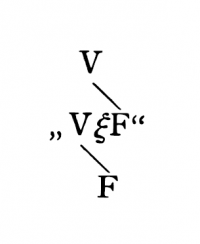
la forma «ξ . η» così:

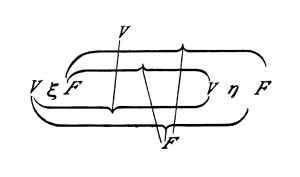
Perciò la proposizione ~(p . ~q) ha questo aspetto:

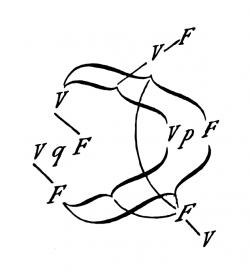
Se inseriamo qui «p» al posto di «q» e controlliamo il collegamento delle V e F più esterne con le più interne, risulta che la verità dell'intera proposizione è associata a tutte le combinazioni di verità del suo argomento, la sua falsità a nessuna delle combinazioni di verità.

6.121 Le proposizioni della logica dimostrano le proprietà logiche delle proposizioni collegandole a formare proposizioni che non dicono nulla.

Questo metodo potrebbe anche essere chiamato un metodo di annullamento. Nella proposizione logica le proposizioni vengono portate all'equilibrio reciproco e lo stato di equilibrio mostra allora come logicamente queste proposizioni devono essere costruite.

[Espandi]6.122 Da ciò risulta che possiamo anche fare a meno delle proposizioni logiche, poiché in una notazione adeguata possiamo riconoscere le proprietà formali delle proposizioni col semplice guardare queste proposizioni.

6.1221 Se ad es. da due proposizioni «p» e «q» nel collegamento «p ⊃ q» risulta una tautologia, allora è chiaro che q segue da p.

Vediamo ad es. che «q» segue da «p ⊃ q . p» da queste due proposizioni stesse, ma possiamo mostrarlo anche così: collegandole in «p ⊃ q . p :⊃:q» e mostrando ora che questa è una tautologia.

6.1222 Questo getta luce sulla questione del motivo per cui le proposizioni logiche non possono essere confermate attraverso l'esperienza – non più di quanto possono essere confutate attraverso l'esperienza. Non solo una proposizione della logica deve non poter essere confutata attraverso alcuna possibile esperienza, ma non le è neanche lecito poterne essere confermata.

6.1223 Ora diviene chiaro perché si è spesso avuta la sensazione che le «verità logiche» dovessero essere da noi «postulate»: possiamo infatti postularle nella stessa misura in cui possiamo postulare una notazione soddisfacente.

6.1224 E diviene ora chiaro anche perché la logica è stata chiamata la teoria delle forme e dell'inferenza.

[Espandi]6.123 È chiaro: le leggi logiche non possono sottostare esse stesse a loro volta a leggi logiche.

(Non vi è, come riteneva Russell, una legge della contraddizione propria di ogni «type»: una sola basta, poiché non viene applicata a se stessa.)

6.1231 La caratteristica della proposizione logica non è la validità generale.

Essere generale infatti vuol dire solo: valere casualmente per tutte le cose. Una proposizione non generalizzata può essere tautologica tanto quanto una generalizzata.

6.1232 La validità generale logica potrebbe essere chiamata essenziale, in contrapposizione a quella casuale per esempio della proposizione «tutti gli uomini sono mortali». Proposizioni come l'«axiom of reducibility» di Russell non sono proposizioni logiche, e questo spiega la nostra sensazione che esse, se anche fossero vere, non potrebbero essere vere che per un caso fortunato.

6.1233 Si può pensare un mondo in cui l'axiom of reducibility non vale. È chiaro però che la logica non ha niente a che fare con la questione se il nostro mondo sia o meno realmente così.

6.124 Le proposizioni logiche descrivono l'impalcatura del mondo, o meglio la presentano. Esse non «trattano» di niente. Esse presuppongono che i nomi abbiano significato e le proposizioni elementari senso: e questa è la loro connessione con il mondo. Chiaramente il fatto che certe connessioni di simboli – che hanno essenzialmente un determinato carattere – siano tautologie deve mostrare qualcosa sul mondo. Qui sta il punto decisivo. Abbiamo detto che qualcosa nei simboli che utilizziamo è arbitrario, qualcosa no. Nella logica è solo questo[, solo ciò che non è arbitrario,] a esprimere: ma ciò vuol dire che nella logica non siamo noi a esprimere, con l'aiuto dei segni, ciò che vogliamo; nella logica ad asserire è piuttosto la natura stessa dei segni per natura necessari: se conosciamo la sintassi logica di un qualsiasi linguaggio segnico, allora sono già date tutte le proposizioni della logica.

[Espandi]6.125 È possibile (in effetti anche secondo la vecchia concezione della logica) dare fin dall'inizio una descrizione di tutte le proposizioni logiche «vere».

6.1251 Per questo nella logica non possono neanche mai esservi sorprese.

[Espandi]6.126 Si può calcolare se una proposizione appartiene alla logica calcolando le proprietà logiche del simbolo.

E questo facciamo quando «dimostriamo» una proposizione logica. Poiché, senza occuparci di un senso e di un significato, formiamo la proposizione logica a partire da altre secondo semplici regole segniche.

La dimostrazione delle proposizioni logiche consiste nel fatto che le facciamo risultare da altre proposizioni logiche attraverso l'applicazione successiva di certe operazioni che, a partire dalle prime, generano sempre di nuovo tautologie. (In effetti da una tautologia seguono solo tautologie.)

Naturalmente questo modo di mostrare che le sue proposizioni sono tautologie è perfettamente inessenziale alla logica, non fosse che perché le proposizioni da cui parte la dimostrazione devono mostrare, senza alcuna dimostrazione, di essere tautologie.

6.1261 Nella logica processo e risultato sono equivalenti. (Per questo nessuna sorpresa.)

6.1262 Nella logica la dimostrazione è solo uno strumento meccanico per riconoscere più facilmente la tautologia là dove essa è complicata.

6.1263 Sarebbe inoltre troppo strano se si potesse dimostrare logicamente a partire da altre una proposizione dotata di senso e anche una proposizione logica. È chiaro fin dall'inizio che la dimostrazione logica di una proposizione dotata di senso e la dimostrazione nella logica devono essere due cose del tutto diverse.

6.1264 La proposizione dotata di senso asserisce qualcosa, e la sua dimostrazione mostra che ciò è così; nella logica ogni proposizione è la forma di una dimostrazione.

Ogni proposizione della logica è un modus ponens presentato in segni. (E non si può esprimere il modus ponens con una proposizione.)

6.1265 Si può sempre concepire la logica in modo tale che ogni proposizione sia la propria dimostrazione.

[Espandi]6.127 Tutte le proposizioni della logica hanno lo stesso rango; non vi sono tra esse per essenza leggi fondamentali e proposizioni derivate.

Ogni tautologia mostra da sé di essere una tautologia.

6.1271 È chiaro che il novero delle «leggi logiche fondamentali» è arbitrario, poiché si potrebbe derivare la logica da una sola legge fondamentale, semplicemente formando ad es. il prodotto logico delle leggi fondamentali di Frege. (Frege direbbe forse che questa legge fondamentale allora non sarebbe più immediatamente evidente. Ma è strano che un pensatore così esatto come Frege si sia richiamato al grado di evidenza come criterio della proposizione logica.)

6.13 La logica non è una teoria, ma un'immagine speculare del mondo.

La logica è trascendentale.

[Espandi]6.2 La matematica è un metodo logico.

Le proposizioni della matematica sono equazioni e quindi pseudo-proposizioni.

[Espandi]6.21 La proposizione della matematica non esprime alcun pensiero.

6.211 Nella vita invero non è mai della proposizione matematica che abbiamo bisogno; al contrario usiamo la proposizione matematica solo per concludere da proposizioni che non appartengono alla matematica ad altre che ugualmente non appartengono alla matematica.

(Nella filosofia la domanda «per cosa utilizziamo propriamente quella parola, quella proposizione?» conduce sempre di nuovo a risultati di grande valore.)

6.22 La logica del mondo, che le proposizioni della logica mostrano nelle tautologie, è mostrata dalla matematica nelle equazioni.

[Espandi]6.23 Se due espressioni vengono collegate dal segno di uguaglianza ciò vuol dire che possono essere sostituite l'una con l'altra. Se però questo si verifica deve mostrarsi nelle due espressioni stesse.

Che esse possano essere sostituite l'una con l'altra caratterizza la forma logica di due proposizioni.

6.231 È una proprietà dell'affermazione che essa possa essere concepita come doppia negazione.

È una proprietà di «1 + 1 + 1 + 1» che essa possa essere concepita come «(1 + 1) + (1 + 1)».

[Espandi]6.232 Frege dice che le due espressioni hanno lo stesso significato, ma senso diverso.

L'essenziale nell'equazione è però che essa non è necessaria per mostrare che le due espressioni collegate dal segno di uguaglianza hanno lo stesso significato, poiché questo può essere visto dalle due espressioni stesse.

6.2321 E che le proposizioni della matematica possano essere dimostrate non vuol dire altro se non che la loro correttezza è da vedersi senza che ciò stesso che esse esprimono debba essere confrontato con i fatti per sincerarsi della sua correttezza.

6.2322 L'identità del significato di due espressioni non può essere asserita. Poiché per poter asserire qualcosa sul loro significato devo conoscere il loro significato: e conoscendo il loro significato so se esse significano lo stesso o qualcosa di diverso.

6.2323 L'equazione caratterizza solo il punto di vista dal quale io considero le due espressioni, cioè dal punto di vista dell'uguaglianza del loro significato.

[Espandi]6.233 La questione se per la soluzione dei problemi matematici vi sia bisogno dell'intuizione dev'essere risolta con ciò: che proprio il linguaggio offre qui l'intuizione necessaria.

6.2331 Il processo del calcolare trasmette appunto questa intuizione.

Il calcolo non è un esperimento.

[Espandi]6.234 La matematica è un metodo della logica.

6.2341 L'essenziale del metodo matematico è questo: lavorare con equazioni. Su questo metodo si basa cioè il fatto che ogni proposizione della matematica deve comprendersi da sé.

[Espandi]6.24 Il metodo della matematica per arrivare alle sue equazioni è il metodo di sostituzione.

Le equazioni infatti esprimono la sostituibilità di due espressioni e noi procediamo da un certo novero di equazioni a equazioni nuove sostituendo espressioni con altre [espressioni] in accordo con le equazioni.

6.241 La dimostrazione della proposizione 2 × 2 = 4 ha questo aspetto:

[math]\displaystyle{ ( \Omega^{ \nu} )^{\mu \prime} x = \Omega^{ \nu \times \mu \prime} x \text{ Def.} }[/math]

[math]\displaystyle{ \Omega^{2 \times 2 \prime} x = (\Omega^2 )^{2 \prime} x = ( \Omega^2 )^{1+1 \prime} x = \Omega^{2 \prime} \Omega^{2 \prime} x = \Omega^{1 + 1 \prime} \Omega^{1 + 1 \prime} x }[/math]

[math]\displaystyle{ (\Omega ' \Omega)^{\prime} (\Omega ' \Omega)^{\prime} x = \Omega ' \Omega ' \Omega ' \Omega ' x = \Omega^{1 + 1 + 1 + 1 \prime} x = \Omega^{4 \prime} x }[/math]

[Espandi]6.3 L'esplorazione della logica significa l'esplorazione di tutte le conformità a leggi. E al di fuori della logica tutto è caso.

6.31 La cosiddetta legge dell'induzione non può certamente essere una legge logica, poiché è evidentemente una proposizione dotata di senso. – E perciò non può neanche essere una legge a priori.

[Espandi]6.32 La legge di causalità non è una legge, ma la forma di una legge.

[Espandi]6.321 «Legge di causalità», ecco il nome di un genere. E come nella meccanica vi sono, diciamo, leggi di minimo – per esempio di minima azione – così nella fisica vi sono leggi di causalità, leggi della forma della causalità.

6.3211 In effetti l'idea che dovesse esservi una «legge di minima azione» è anche stata intrattenuta prima che si sapesse che aspetto essa aveva. (Qui, come sempre, ciò che è certo a priori si rivela essere qualcosa di puramente logico.)

6.33 Non crediamo a priori in una legge di conservazione, bensì conosciamo a priori la possibilità di una forma logica.

[Espandi]6.34 Tutti quei principi, come il principio di ragione, di continuità nella natura, di minimo sforzo nella natura ecc. ecc., tutte queste sono intuizioni a priori circa la forma che possono assumere le proposizioni della scienza.

6.341 La meccanica newtoniana ad es. porta la descrizione del mondo a una forma unitaria. Immaginiamo una superficie bianca sulla quale vi siano macchie nere irregolari. Diciamo ora: qualunque immagine ne risulti, io posso sempre approssimarmi a piacere alla sua descrizione ricoprendo la superficie con un reticolo quadrato adeguatamente fine e dicendo quindi di ogni quadrato che è bianco o che è nero. In tal modo avrò portato la descrizione della superficie a una forma unitaria. Questa forma è arbitraria, poiché con uguale successo avrei potuto utilizzare una rete dalle maglie triangolari o esagonali. Può essere che la descrizione per mezzo di una rete di triangoli sarebbe risultata più semplice; ciò vuol dire che avremmo potuto descrivere la superficie più esattamente con una rete di triangoli più grossa che con una più fine di quadrati (o viceversa), e così via. Alle diverse reti corrispondono diversi sistemi per la descrizione del mondo. La meccanica determina una forma della descrizione del mondo dicendo: tutte le proposizioni della descrizione del mondo devono essere ottenute da un novero di proposizioni date – gli assiomi meccanici – in un dato modo. In questo modo essa offre i mattoni per la costruzione dell'edificio scientifico e dice: qualunque edificio tu voglia mai erigere, devi metterlo insieme in qualche maniera con questi mattoni e solo con questi.

(Come con il sistema dei numeri [si deve poter scrivere] ogni numero che si voglia, così con il sistema della meccanica si deve poter scrivere ogni proposizione della fisica che si voglia.)

6.342 E ora vediamo la posizione reciproca di logica e meccanica. (Si potrebbe far consistere la rete anche di figure eterogenee, per esempio di triangoli ed esagoni.) Che un'immagine come quella menzionata or ora possa essere descritta mediante una rete di forma data non asserisce niente sull'immagine. (Poiché ciò vale per ogni immagine di questo tipo.) Questo però caratterizza l'immagine: che essa può essere completamente descritta mediante una determinata rete di determinata finezza.

Così, neanche il fatto che il mondo possa essere descritto mediante la meccanica newtoniana asserisce alcunché su di esso; asserisce però qualcosa il fatto che esso possa essere descritto così dalla meccanica newtoniana come appunto può esserlo. E dice qualcosa sul mondo anche il fatto che esso possa essere descritto più semplicemente mediante una certa meccanica che mediante un'altra.

[Espandi]6.343 La meccanica è un tentativo di costruire secondo un unico piano tutte le proposizioni vere di cui abbiamo bisogno per la descrizione del mondo.

6.3431 Mediante l'intero apparato logico, le leggi fisiche parlano pur sempre degli oggetti del mondo.

6.3432 Non possiamo dimenticare che la descrizione del mondo mediante la meccanica è sempre una descrizione del mondo del tutto generale. In essa ad es. non si parla mai di determinati punti materiali, bensì sempre di punti materiali qualsiasi.

6.35 Benché le macchie nella nostra immagine siano figure geometriche, evidentemente la geometria non può dire proprio niente sulla loro forma e sul loro luogo fattuali. La rete tuttavia è puramente geometrica, tutte le sue proprietà possono essere indicate a priori.

Leggi come il principio di ragione ecc. trattano della rete, non di ciò che la rete descrive.

[Espandi]6.36 Se vi fosse una legge di causalità, essa potrebbe avere questo aspetto: «Vi sono leggi naturali».

Ma ciò non può certo essere detto: ciò si mostra.

[Espandi]6.361 Secondo il modo di esprimersi di Hertz si potrebbe dire: solo le connessioni conformi a leggi sono pensabili.

[Espandi]6.3611 Non possiamo paragonare alcun processo con lo «scorrere del tempo» – questo non vi è –, bensì solo con un altro processo (per esempio con il procedere del cronometro).

Perciò la descrizione del passare del tempo è possibile solo se ci appoggiamo a un altro processo.

Per lo spazio vale qualcosa di perfettamente analogo. Dove ad es. si dice che non può accadere nessuno di due eventi (che si escludono a vicenda) perché non esiste una causa per cui dovrebbe accadere l'uno piuttosto che l'altro, là si tratta in realtà di questo: che non si può affatto descrivere uno dei due eventi se non esiste una qualche asimmetria. E se una tale asimmetria esiste, allora possiamo concepirla come causa dell'accadere dell'uno e del non-accadere dell'altro.

6.36111 Il problema kantiano della mano destra e sinistra che non si possono sovrapporre sussiste già nel piano, anzi già nello spazio unidimensionale, dove anche le due figure congruenti a e b non possono essere sovrapposte senza essere tirate fuori da questo spazio.

La mano destra e sinistra sono di fatto perfettamente congruenti. E che non si possa sovrapporle non ha con ciò niente a che fare.

Si potrebbe indossare il guanto destro sulla mano sinistra se si potesse rivoltarlo nello spazio quadridimensionale.

6.362 Ciò che può essere descritto può anche avvenire, e ciò che la legge di causalità deve escludere non può nemmeno essere descritto.

[Espandi]6.363 Il processo dell'induzione consiste nel nostro accettare la legge che è più semplice da armonizzare con le nostre esperienze.

[Espandi]6.3631 Questo processo non ha però un fondamento logico, ma solo psicologico.

È chiaro che non esiste alcuna ragione per credere che avverrà davvero il caso più semplice.

6.36311 Che il sole domani sorgerà è un'ipotesi; e questo vuol dire: non sappiamo se sorgerà.

[Espandi]6.37 Una coercizione per cui qualcosa debba avvenire perché qualcos'altro è avvenuto non vi è. Vi è solo una necessità logica.

6.371 Alla base dell'intera visione moderna del mondo giace l'illusione che le cosiddette leggi naturali siano la spiegazione dei fenomeni naturali.

6.372 Così i moderni stanno al cospetto delle leggi della natura come di qualcosa di sacrosanto, alla stregua degli antichi al cospetto di Dio e del Fato.

Ed entrambi[, moderni e antichi,] hanno al contempo ragione e torto. Gli antichi sono però più chiari in quanto ammettono un chiaro termine [alle spiegazioni], mentre nel nuovo sistema deve sembrare che tutto sia spiegato.

6.373 Il mondo è indipendente dalla mia volontà.

6.374 Anche se tutto ciò che desideriamo avvenisse, questo sarebbe ancora per così dire un dono del destino, poiché a garantirlo non vi è alcuna connessione logica tra volontà e mondo, e, quanto alla connessione fisica stessa che viene assunta, non potremmo volerla a sua volta.

[Espandi]6.375 Come vi è solo una necessità logica, così vi è anche solo un'impossibilità logica.

6.3751 Che ad es. due colori siano contemporaneamente in un punto del campo visivo è impossibile, cioè logicamente impossibile, perché è escluso dalla struttura logica del colore.

Pensiamo a come questa contraddizione si presenta nella fisica, cioè all'incirca così: una particella non può nello stesso momento avere due velocità; il che vuol dire che essa non può essere al medesimo tempo in due punti diversi; il che vuol dire che particelle che sono in punti diversi in un unico momento non possono essere identiche.

(È chiaro che il prodotto logico di due proposizioni elementari non può essere né una tautologia né una contraddizione. L'asserzione che nello stesso momento un punto del campo visivo ha due colori diversi è una contraddizione.)

[Espandi]6.4 Tutte le proposizioni hanno lo stesso valore.

6.41 Il senso del mondo deve trovarsi al di fuori del mondo. Nel mondo tutto è come è e tutto avviene come avviene; non vi è in esso alcun valore – e se vi fosse, non avrebbe alcun valore.

Se vi è un valore che ha valore, esso deve trovarsi al di fuori di tutto l'accadere ed essere-così. Poiché tutto l'accadere e l'essere-così è casuale.

Ciò che lo rende non-casuale non può trovarsi nel mondo, poiché altrimenti sarebbe di nuovo casuale.

Deve trovarsi al di fuori del mondo.

[Espandi]6.42 Perciò non può nemmeno esservi alcuna proposizione dell'etica.

Le proposizioni non possono esprimere niente di ciò che è più elevato.

6.421 È chiaro che l'etica non può essere enunciata.

L'etica è trascendentale.

(Etica ed estetica sono uno.)

6.422 Il primo pensiero di fronte al dispiegamento di una legge etica della forma «tu devi…» è: e allora se non lo faccio? Ma è chiaro che l'etica non ha niente a che fare con punizione e premio nel senso abituale. Quindi tale domanda sulle conseguenze di un'azione dev'essere irrilevante. – Quanto meno queste conseguenze non possono essere eventi. Poiché qualcosa deve pur essere corretto nella formulazione di quella domanda. Deve, sì, esservi una sorta di premio etico e di punizione etica, ma questi devono giacere nell'azione stessa.

(Ed è chiaro anche che il premio dev'essere qualcosa di gradevole, la punizione qualcosa di sgradevole.)

6.423 Della volontà come del portatore di ciò che è etico non si può parlare.

E la volontà come fenomeno interessa solo la psicologia.

[Espandi]6.43 Se il volere buono o cattivo modifica il mondo, esso può modificare solo i limiti del mondo, non i fatti; non ciò che può essere espresso mediante il linguaggio.

In breve, il mondo deve allora divenire per mezzo del volere un mondo del tutto diverso. Deve, per così dire, ridursi o crescere come intero.

Il mondo di colui che è felice è un mondo diverso rispetto a quello di colui che è infelice.

[Espandi]6.431 Come anche, con la morte, il mondo non si modifica, ma finisce.

6.4311 La morte non è un evento della vita. Non si vive la morte.

Se per eternità non si intende durata temporale infinita, ma intemporalità, allora vive in eterno colui che vive nel presente.

La nostra vita è tanto priva di fine quanto il nostro campo visivo è privo di limite.

6.4312 L'immortalità temporale dell'anima umana, cioè quindi la sua sopravvivenza eterna anche dopo la morte, non solo non è in alcun modo garantita, ma soprattutto è un'assunzione che non realizza affatto ciò che si è sempre voluto ottenere grazie a essa. Col mio sopravvivere in eterno si risolve forse un enigma? Non è questa vita eterna tanto enigmatica quanto la presente? La soluzione dell'enigma della vita nello spazio e nel tempo si trova al di fuori di spazio e tempo.

(Quelli che qui vanno risolti non sono problemi della scienza naturale.)

[Espandi]6.432 Come è il mondo è perfettamente indifferente per ciò che è più elevato. Dio non si manifesta nel mondo.

6.4321 I fatti appartengono tutti solo al problema, non alla soluzione.

6.44 Non come è il mondo, ma che esso è, è il mistico.

6.45 La visione del mondo sub specie aeterni è la sua visione come tutto – limitato.

Il sentimento del mondo come tutto limitato è il sentimento mistico.

[Espandi]6.5 Per una risposta che non si può formulare non si può formulare neanche la domanda.

L'enigma non vi è.

Se è possibile porre una data domanda, essa può anche avere risposta.

6.51 Lo scetticismo non è inconfutabile, bensì evidentemente insensato, se vuole dubitare dove non si può domandare.

Il dubbio può sussistere solo dove sussiste una domanda; una domanda solo dove sussiste una risposta e questa solo dove qualcosa può essere detto.

[Espandi]6.52 Noi sentiamo che, anche se si dà risposta a tutte le domande scientifiche possibili, i problemi della nostra vita non risultano ancora neanche toccati. Certo non rimane allora proprio nessuna domanda; e proprio questa è la risposta.

6.521 La soluzione del problema della vita si coglie al dissolversi di tale problema.

(Non è questa la ragione per cui coloro a cui il senso della vita divenne chiaro dopo lungo dubitare poi non seppero dire in cosa questo senso consistesse?)

6.522 Vi è in effetti qualcosa di indicibile. Ciò si mostra, è il mistico.

6.53 Il metodo corretto della filosofia sarebbe propriamente questo: non dire niente se non ciò che può essere detto, cioè proposizioni della scienza naturale – cioè qualcosa che con la filosofia non ha niente a che fare –, e poi tutte le volte che qualcun altro volesse dire qualcosa di metafisico provargli che a certi segni nelle sue proposizioni egli non ha dato alcun significato. Questo metodo sarebbe per l'altro insoddisfacente – egli non avrebbe la sensazione che noi gli stiamo insegnando la filosofia – ma esso sarebbe l'unico rigorosamente corretto.

6.54 Le mie proposizioni chiarificano qualcosa perché colui che mi comprende le riconosce, alla fine, come insensate, quando egli attraverso esse – su di esse – è salito oltre esse. (Egli deve per così dire gettar via la scala dopo averla usata per salire.)

Egli deve oltrepassare queste proposizioni, e allora vede il mondo correttamente.

7 Di ciò di cui non si può parlare si deve tacere.

---