Philosophische Untersuchungen: Difference between revisions
No edit summary |
No edit summary |
||
| Line 438: | Line 438: | ||
{{PU 48-2}} | {{PU 48-2}} | ||
Hier ist der Satz ein Komplex von Namen, dem ein Komplex von Elementen entspricht. Die Urelemente sind die farbigen Quadrate. »Aber sind diese einfach?« – Ich wüßte nicht, was ich in diesem Sprachspiel natürlicher das »Einfache« nennen sollte. Unter anderen Umständen aber würde ich ein einfarbiges Quadrat »zusammengesetzt« nennen, etwa aus zwei Rechtecken, oder aus den Elementen Farbe und Form. Aber der Begriff der Zusammensetzung könnte auch so gedehnt werden, daß die kleinere Fläche ›zusammengesetzt‹ genannt wird aus einer größeren und einer von ihr subtrahierten. Vergleiche ›Zusammensetzung‹ der Kräfte, ›Teilung‹ einer Strecke durch einen Punkt außerhalb; diese Ausdrücke zeigen, daß wir unter Umständen auch geneigt sind, das Kleinere als Resultat der Zusammensetzung von Größerem aufzufassen und das Größere als ein Resultat der Teilung des Kleineren. | |||
Aber ich weiß nicht, ob ich nun sagen soll, die Figur, die unser Satz beschreibt, bestehe aus vier Elementen oder aus neun! Nun, besteht jener Satz aus vier Buchstaben oder aus neun? – Und welches sind ''seine'' Elemente: die Buchstabentypen, oder die Buchstaben? Ist es nicht gleichgültig, welches wir sagen? wenn wir nur im besonderen Fall Mißverständnisse vermeiden! | |||
'''49'''. Was heißt es aber, daß wir diese Elemente nicht erklären (d.h. beschreiben) sondern nur benennen können? Das könnte etwa sagen, daß die Beschreibung eines Komplexes, wenn er, in einem Grenzfall, nur aus ''einem'' Quadrat besteht, einfach der Name des Farbquadrates ist. | |||
Man könnte hier sagen – obwohl dies leicht zu allerlei philosophischem Aberglauben führt – ein Zeichen »R«, oder »S«, etc., könne einmal Wort und einmal Satz sein. Ob es aber ›Wort oder Satz ist‹, hängt von der Situation ab, in der es ausgesprochen oder geschrieben wird. Soll z. B. A dem B Komplexe von Farbquadraten beschreiben und gebraucht er hier das Wort »R« ''allein'', so werden wir sagen können, das Wort sei eine Beschreibung – ein Satz. Memoriert er aber etwa die Wörter und ihre Bedeutungen, oder lehrt er einen Andern den Gebrauch der Wörter und spricht sie beim hinweisenden Lehren aus, so werden wir nicht sagen, sie seien hier Sätze. In dieser Situation ist das Wort »R« z.B. keine Beschreibung; man ''benennt'' damit ein Element –– aber darum wäre es hier seltsam zu sagen, das Element könne man ''nur'' benennen! Benennen und Beschreiben stehen ja nicht auf ''einer'' Ebene: Das Benennen ist eine Vorbereitung zur Beschreibung. Das Benennen ist noch gar kein Zug im Sprachspiel, – so wenig, wie das Aufstellen einer Schachfigur ein Zug im Schachspiel. Man kann sagen: Mit dem Benennen eines Dings ist noch ''nichts'' getan. Es ''hat'' auch keinen Namen, außer im Spiel. Das war es auch, was Frege damit meinte: ein Wort habe nur im Satzzusammenhang Bedeutung. | |||
'''50'''. Was heißt es nun, von den Elementen zu sagen, daß wir ihnen weder Sein noch Nichtsein beilegen können? – Man könnte sagen: Wenn alles, was wir »Sein« oder »Nichtsein« nennen, im Bestehen und Nichtbestehen von Verbindungen zwischen den Elementen liegt, dann hat es keinen Sinn vom Sein (Nichtsein) eines Elements zu sprechen; sowie, wenn alles, was wir »zerstören« nennen, in der Trennung von Elementen liegt, es keinen Sinn hat, vom Zerstören eines Elements zu reden. | |||
Aber man möchte sagen: Man kann dem Element nicht Sein beilegen, denn ''wäre'' es nicht, so könnte man es auch nicht einmal nennen und also gar nichts von ihm aussagen. – Betrachten wir doch einen analogen Fall! Man kann von ''einem'' Ding nicht aussagen, es sei 1 m lang, noch, es sei nicht 1 m lang, und das ist das Urmeter in Paris. – Damit haben wir aber diesem natürlich nicht irgend eine merkwürdige Eigenschaft zugeschrieben, sondern nur seine eigenartige Rolle im Spiel des Messens mit dem Metermaß gekennzeichnet. – Denken wir uns auf ähnliche Weise wie das Urmeter auch die Muster von Farben in Paris aufbewahrt. So erklären wir: »Sepia« heiße die Farbe des dort unter Luftabschluß aufbewahrten Ur-Sepia. Dann wird es keinen Sinn haben, von diesem Muster auszusagen, es habe diese Farbe, noch, es habe sie nicht. | |||
Wir können das so ausdrücken: Dieses Muster ist ein Instrument der Sprache, mit der wir Farbaussagen machen. Es ist in diesem Spiel nicht Dargestelltes, sondern Mittel der Darstellung. – Und eben das gilt von einem Element im Sprachspiel (48), wenn wir, es benennend, das Wort »R« aussprechen: wir haben damit diesem Ding eine Rolle in unserm Sprachspiel gegeben; es ist nun ''Mittel'' der Darstellung. Und zu sagen »''Wäre'' es nicht, so könnte es keinen Namen haben« sagt nun so viel, und so wenig, wie: gäbe es dieses Ding nicht, so könnten wir es in unserem Spiel nicht verwenden. – Was es, scheinbar, geben ''muß'', gehört zur Sprache. Es ist in unserem Spiel ein Paradigma; etwas, womit verglichen wird. Und dies feststellen, kann heißen, eine wichtige Feststellung machen; aber es ist dennoch eine Feststellung unser Sprachspiel – unsere Darstellungsweise – betreffend. | |||
'''51'''. In der Beschreibung des Sprachspiels (48) sagte ich, den Farben der Quadrate entsprächen die Wörter »R«, »S«, etc. Worin aber besteht diese Entsprechung, in wiefern kann man sagen, diesen Zeichen entsprächen gewisse Farben der Quadrate? Die Erklärung in (48) stellte ja nur einen Zusammenhang zwischen diesen Zeichen und gewissen Wörtern unserer Sprache her (den Farbnamen). – Nun, es war vorausgesetzt, daß der Gebrauch der Zeichen im Spiel anders, und zwar durch Hinweisen auf Paradigmen, gelehrt würde. Wohl; aber was heißt es nun, zu sagen, in der ''Praxis der Sprache'' entsprächen den Zeichen gewisse Elemente? – Liegt es darin, daß der, welcher die Komplexe von Farbquadraten beschreibt, hierbei immer »R« sagt, wo ein rotes Quadrat steht; »S«, wo ein schwarzes steht, etc.? Aber wie, wenn er sich bei der Beschreibung irrt und, fälschlich, »R« sagt, wo er ein schwarzes Quadrat sieht –– was ist hier das Kriterium dafür, daß dies ein ''Fehler'' war? – Oder besteht, daß »R« ein rotes Quadrat bezeichnet, darin, daß den Menschen, die die Sprache gebrauchen, immer ein rotes Quadrat im Geist vorschwebt, wenn sie das Zeichen »R« gebrauchen? | |||
Um klarer zu sehen, müssen wir hier, wie in unzähligen ähnlichen Fällen, die Einzelheiten der Vorgänge ins Auge fassen; was vorgeht ''aus der Nähe betrachten''. | |||
'''52'''. Wenn ich dazu neige, anzunehmen, daß eine Maus durch Urzeugung aus grauen Fetzen und Staub entsteht, so wird es gut sein, diese Fetzen genau daraufhin zu untersuchen, wie eine Maus sich in ihnen verstecken konnte, wie sie dort hinkommen konnte, etc. Bin ich aber überzeugt, daß eine Maus aus diesen Dingen nicht entstehen kann, dann wird diese Untersuchung vielleicht überflüssig sein. | |||
Was es aber ist, das sich in der Philosophie einer solchen Betrachtung der Einzelheiten entgegensetzt, müssen wir erst verstehen lernen. | |||
'''53'''. Es gibt nun ''verschiedene'' Möglichkeiten für unser Sprachspiel (48), verschiedene Fälle, in denen wir sagen würden, ein Zeichen benenne in dem Spiel ein Quadrat von der und der Farbe. Wir würden dies z.B. sagen, wenn wir wüßten, daß den Menschen, die diese Sprache gebrauchen, der Gebrauch der Zeichen auf die und die Art beigebracht wurde. Oder, wenn es schriftlich, etwa in Form einer Tabelle, niedergelegt wäre, daß diesem Zeichen dieses Element entspricht, und wenn diese Tabelle beim Lehren der Sprache benützt und in gewissen Streitfällen zur Entscheidung herangezogen würde. | |||
Wir können uns aber auch denken, daß eine solche Tabelle ein Werkzeug im Gebrauch der Sprache ist. Die Beschreibung eines Komplexes geht dann so vor sich: Der den Komplex beschreibt, führt eine Tabelle mit sich und sucht in ihr jedes Element des Komplexes auf und geht von ihm in der Tabelle zum Zeichen über (und es kann auch der, dem die Beschreibung gegeben wird, die Worte derselben durch eine Tabelle in die Anschauung von farbigen Quadraten übersetzen). Man könnte sagen, diese Tabelle übernehme hier die Rolle, die in anderen Fällen Gedächtnis und Assoziation spielen. (Wir werden den Befehl »Bring mir eine rote Blume!« für gewöhnlich nicht so ausführen, daß wir die Farbe Rot in einer Farbentabelle aufsuchen und dann eine Blume bringen von der Farbe, die wir in der Tabelle finden; aber wenn es sich darum handelt, einen bestimmten Ton von Rot zu wählen, oder zu mischen, dann geschieht es, daß wir uns eines Musters oder einer Tabelle bedienen.) | |||
Nennen wir eine solche Tabelle den Ausdruck einer Regel des Sprachspiels, so kann man sagen, daß dem, was wir Regel eines Sprachspiels nennen, sehr verschiedene Rollen im Spiel zukommen können. | |||
'''54'''. Denken wir doch daran, in was für Fällen wir sagen, ein Spiel werde nach einer bestimmten Regel gespielt! | |||
Die Regel kann ein Behelf des Unterrichts im Spiel sein. Sie wird dem Lernenden mitgeteilt und ihre Anwendung eingeübt. – Oder sie ist ein Werkzeug des Spieles selbst. – Oder: Eine Regel findet weder im Unterricht noch im Spiel selbst Verwendung; noch ist sie in einem Regelverzeichnis niedergelegt. Man lernt das Spiel, indem man zusieht, wie Andere es spielen. Aber wir sagen, es werde nach den und den Regeln gespielt, weil ein Beobachter diese Regeln aus der Praxis des Spiels ablesen kann, – wie ein Naturgesetz, dem die Spielhandlungen folgen. –– Wie aber unterscheidet der Beobachter in diesem Fall zwischen einem Fehler der Spielenden und einer richtigen Spielhandlung? – Es gibt dafür Merkmale im Benehmen der Spieler. Denke an das charakteristische Benehmen dessen, der ein Versprechen korrigiert. Es wäre möglich, zu erkennen, daß Einer dies tut, auch wenn wir seine Sprache nicht verstehen. | |||
'''55'''. »Was die Namen der Sprache bezeichnen, muß unzerstörbar sein: denn man muß den Zustand beschreiben können, in dem alles, was zerstörbar ist, zerstört ist. Und in dieser Beschreibung wird es Wörter geben; und was ihnen entspricht, darf dann nicht zerstört sein, denn sonst hätten die Wörter keine Bedeutung.« Ich darf mir nicht den Ast absägen, auf welchem ich sitze. | |||
Man könnte nun freilich gleich einwenden, daß ja die Beschreibung selbst sich von der Zerstörung ausnehmen müsse. – Aber das, was den Wörtern der Beschreibung entspricht und also nicht zerstört sein darf, wenn sie wahr ist, ist, was den Wörtern ihre Bedeutung gibt, – ohne welches sie keine Bedeutung hätten. –– Aber dieser Mensch ist ja doch in einem Sinne das, was seinem Namen entspricht. Er aber ist zerstörbar; und sein Name verliert seine Bedeutung nicht, wenn der Träger zerstört wird. – Das, was dem Namen entspricht, und ohne den er keine Bedeutung hätte, ist, z.B., ein Paradigma, das im Sprachspiel in Verbindung mit dem Namen gebraucht wird. | |||
'''56'''. Aber wie, wenn kein solches Muster zur Sprache gehört, wenn wir uns, z. B., die Farbe, die ein Wort bezeichnet, ''merken''? –– »Und wenn wir sie uns merken, so tritt sie also vor unser geistiges Auge, wenn wir etwa das Wort aussprechen. Sie muß also an sich unzerstörbar sein, wenn die Möglichkeit bestehen soll, daß wir uns jederzeit an sie erinnern.« –– Aber was sehen wir denn als das Kriterium dafür an, daß wir uns richtig an sie erinnern? – Wenn wir mit einem Muster statt mit unserm Gedächtnis arbeiten, so sagen wir unter Umständen, das Muster habe seine Farbe verändert und beurteilen dies mit dem Gedächtnis. Aber können wir nicht unter Umständen auch von einem Nachdunkeln (z.B.) unseres Erinnerungsbildes reden? Sind wir dem Gedächtnis nicht ebenso ausgeliefert wie einem Muster? (Denn es könnte Einer sagen wollen: »Wenn wir kein Gedächtnis hätten, wären wir einem Muster ausgeliefert.«) – Oder etwa einer chemischen Reaktion. Denke, du solltest eine bestimmte Farbe »F« malen, und es ist die Farbe, welche man sieht, wenn sich die chemischen Substanzen X und Y miteinander verbinden. – Nimm an, die Farbe käme dir an einem Tag heller vor als an einem andern; würdest du da nicht unter Umständen sagen: »Ich muß mich irren, die Farbe ist gewiß die gleiche wie gestern«? Das zeigt, daß wir uns dessen, was das Gedächtnis sagt, nicht immer als des obersten, inappellabeln, Schiedsspruchs bedienen. | |||
'''57'''. »Etwas Rotes kann zerstört werden, aber Rot kann nicht zerstört werden, und darum ist die Bedeutung des Wortes ›rot‹ von der Existenz eines roten Dinges unabhängig.« – Gewiß, es hat keinen Sinn, zu sagen, die Farbe Rot (color, nicht pigmentum) werde zerrissen, oder zerstampft. Aber sagen wir nicht, »Die Röte verschwindet«? Und klammre dich nicht daran, daß wir sie uns vors geistige Auge rufen können, auch wenn es nichts Rotes mehr gibt! Dies ist nicht anders, als wolltest du sagen, daß es dann immer noch eine chemische Reaktion gäbe, die eine rote Flamme erzeugt. – Denn wie, wenn du dich nicht mehr an die Farbe erinnern kannst? – Wenn wir vergessen, welche Farbe es ist, die diesen Namen hat, so verliert er seine Bedeutung für uns; d.h., wir können ein bestimmtes Sprachspiel nicht mehr mit ihm spielen. Und die Situation ist dann der zu vergleichen, daß das Paradigma, welches ein Mittel unserer Sprache war, verlorengegangen ist. | |||
'''58'''. »Ich will ›''Name''‹ nur das nennen, was nicht in der Verbindung ›X existiert‹ stehen kann. – Und so kann man nicht sagen ›Rot existiert‹, weil, wenn es Rot nicht gäbe, von ihm überhaupt nicht geredet werden könnte.« – Richtiger: Wenn »X existiert« soviel besagen soll, wie: »X« habe Bedeutung, – dann ist es kein Satz, der von X handelt, sondern ein Satz über unsern Sprachgebrauch, nämlich den Gebrauch des Wortes »X«. | |||
Es erscheint uns, als sagten wir damit etwas über die Natur von Rot: daß die Worte »Rot existiert« keinen Sinn ergeben. Es existiere eben ›an und für sich‹. Die gleiche Idee, – daß dies eine metaphysische Aussage über Rot ist, – drückt sich auch darin aus, daß wir etwa sagen, Rot sei zeitlos, und vielleicht noch stärker im Wort »unzerstörbar«. | |||
Aber eigentlich ''wollen'' wir eben nur »Rot existiert« auffassen als Aussage: das Wort »Rot« hat Bedeutung. Oder vielleicht richtiger: »Rot existiert nicht« als » ›Rot‹ hat keine Bedeutung«. Nur wollen wir nicht sagen, daß jener Ausdruck das ''sagt'', sondern daß er ''das'' sagen müßte, ''wenn'' er einen Sinn hätte. Daß er sich aber beim Versuch, das zu sagen, selbst widerspricht – da eben Rot ›an und für sich‹ sei. Während ein Widerspruch nur etwa darin liegt, daß der Satz aussieht, als rede er von der Farbe, während er etwas über den Gebrauch des Wortes »rot« sagen soll. – In Wirklichkeit aber sagen wir sehr wohl, eine bestimmte Farbe existiere; und das heißt soviel wie: es existiere etwas, was diese Farbe hat. Und der erste Ausdruck ist nicht weniger exakt als der zweite; besonders dort nicht, wo ›das, was die Farbe hat‹, kein physikalischer Gegenstand ist. | |||
'''59'''. »''Namen'' bezeichnen nur das, was ''Element'' der Wirklichkeit ist. Was sich nicht zerstören läßt; was in allem Wandel gleichbleibt.« – Aber was ist das? – Während wir den Satz sagten, schwebte es uns ja schon vor! Wir sprachen schon eine ganz bestimmte Vorstellung aus. Ein bestimmtes Bild, das wir verwenden wollen. Denn die Erfahrung zeigt uns diese Elemente ja nicht. Wir sehen ''Bestandteile'' von etwas Zusammengesetztem (eines Sessels z.B.). Wir sagen, die Lehne ist ein Teil des Sessels, aber selbst wieder zusammengesetzt aus verschiedenen Hölzern; während ein Fuß ein einfacher Bestandteil ist. Wir sehen auch ein Ganzes, was sich ändert (zerstört wird), während seine Bestandteile unverändert bleiben. Dies sind die Materialien, aus denen wir jenes Bild der Wirklichkeit anfertigen. | |||
'''60'''. Wenn ich nun sage: »Mein Besen steht in der Ecke«, – ist dies eigentlich eine Aussage über den Besenstiel und die Bürste des Besens? Jedenfalls könnte man doch die Aussage ersetzen durch eine, die die Lage des Stiels und die Lage der Bürste angibt. Und diese Aussage ist doch nun wie eine weiter analysierte Form der ersten. – Warum aber nenne ich sie »weiter analysiert«? – Nun, wenn der Besen sich dort befindet, so heißt das doch, es müssen Stiel und Bürste dort sein und in bestimmter Lage zueinander; und dies war früher gleichsam im Sinn des Satzes verborgen, und im analysierten Satz ist es ''ausgesprochen''. Also meint der, der sagt, der Besen stehe in der Ecke, eigentlich: der Stiel sei dort und die Bürste, und der Stiel stecke in der Bürste? – Wenn wir jemand fragten, ob er das meint, würde er wohl sagen, daß er gar nicht an den Besenstiel besonders, oder an die Bürste besonders, gedacht habe. Und das wäre die ''richtige'' Antwort, denn er wollte weder vom Besenstiel, noch von der Bürste besonders reden. Denke, du sagtest jemandem statt »Bring mir den Besen!« – »Bring mir den Besenstiel und die Bürste, die an ihm steckt!« – Ist die Antwort darauf nicht: »Willst du den Besen haben? Und warum drückst du das so sonderbar aus?« –– Wird er den weiter analysierten Satz also besser verstehen? – Dieser Satz, könnte man sagen, leistet dasselbe, wie der gewöhnliche, aber auf einem umständlicheren Wege. – Denk dir ein Sprachspiel, in dem jemandem Befehle gegeben werden, gewisse, aus mehreren Teilen zusammengesetzte, Dinge zu bringen, zu bewegen, oder dergleichen. Und zwei Arten es zu spielen: in der einen (a) haben die zusammengesetzten Dinge (Besen, Stühle, Tische, etc.) Namen, wie in (15); in anderen (b) erhalten nur die Teile Namen und das Ganze wird mit ihrer Hilfe beschrieben. – In wiefern ist denn ein Befehl des zweiten Spiels eine analysierte Form eines Befehls des ersten? Steckt denn jener in diesem und wird nun durch Analyse herausgeholt? – Ja, der Besen wird zerlegt, wenn man Stiel und Bürste trennt; aber besteht darum auch der Befehl, den Besen zu bringen, aus entsprechenden Teilen? | |||
'''61'''. »Aber du wirst doch nicht leugnen, daß ein bestimmter Befehl in (a) das Gleiche sagt, wie einer in (b); und wie willst du denn den zweiten nennen, wenn nicht eine analysierte Form des ersten?« – Freilich, ich würde auch sagen, ein Befehl in (a) habe den gleichen Sinn, wie einer in (b); oder, wie ich es früher ausgedrückt habe: sie leisten dasselbe. Und das heißt: Wenn mir etwa ein Befehl in (a) gezeigt und die Frage gestellt würde »Welchem Befehl in (b) ist dieser gleichsinnig?«, oder auch »Welchen Befehlen in (b) widerspricht er?«, so werde ich die Frage so und so beantworten. Aber damit ist nicht gesagt, daß wir uns über die Verwendung des Ausdrucks »den gleichen Sinn haben«, oder »dasselbe leisten« ''im Allgemeinen'' verständigt haben. Man kann nämlich fragen: In welchem Fall sagen wir »Das sind nur zwei verschiedene Formen desselben Spiels«? | |||
'''62'''. Denke etwa, der, dem die Befehle in (a) und (b) gegeben werden, habe in einer Tabelle, welche Namen und Bilder einander zuordnet, nachzusehen, ehe er das Verlangte bringt. Tut er nun ''dasselbe'', wenn er einen Befehl in (a) und den entsprechenden in (b) ausführt? – Ja und nein. Du kannst sagen: »Der ''Witz'' der beiden Befehle ist der gleiche«. Ich würde hier dasselbe sagen. – Aber es ist nicht überall klar, was man den ›Witz‹ des Befehls nennen soll. (Ebenso kann man von gewissen Dingen sagen: ihr Zweck ist der und der. Das Wesentliche ist, daß das eine ''Lampe'' ist, zur Beleuchtung dient –– daß sie das Zimmer schmückt, einen leeren Raum füllt, etc., ist nicht wesentlich. Aber nicht immer sind wesentlich und unwesentlich klar getrennt.) | |||
'''63'''. Der Ausdruck aber, ein Satz in (b) sei eine ›analysierte‹ Form eines in (a), verführt uns leicht dazu, zu meinen, jene Form sei die fundamentalere; sie zeige erst, was mit der andern gemeint sei, etc. Wir denken etwa: Wer nur die unanalysierte Form besitzt, dem geht die Analyse ab; wer aber die analysierte Form kennt, der besitze damit alles. – Aber kann ich nicht sagen, daß ''diesem'' ein Aspekt der Sache verlorengeht, so wie jenem ? | |||
'''64'''. Denken wir uns das Spiel (48) dahin abgeändert, daß in ihm Namen nicht einfarbige Quadrate bezeichnen, sondern Rechtecke, die aus je zwei solchen Quadraten bestehen. Ein solches Rechteck, halb rot, halb grün, heiße »U«; ein Rechteck, halb grün, halb weiß, heiße »V«, etc. Könnten wir uns nicht Menschen denken, die für solche Farbenkombinationen Namen hätten, aber nicht für die einzelnen Farben? Denk an die Fälle, in denen wir sagen: »Diese Farbenzusammenstellung (die französische Trikolore etwa) hat einen ganz besonderen Charakter.« | |||
In wiefern sind die Zeichen dieses Sprachspiels einer Analyse bedürftig? Ja, in wieweit ''kann'' das Spiel durch (48) ersetzt werden? – Es ist eben ein ''anderes'' Sprachspiel; wenn auch mit (48) verwandt. | |||
'''65'''. Hier stoßen wir auf die große Frage, die hinter allen diesen Betrachtungen steht. – Denn man könnte mir einwenden: »Du machst dir’s leicht! Du redest von allen möglichen Sprachspielen, hast aber nirgends gesagt, was denn das Wesentliche des Sprachspiels, und also der Sprache, ist. Was allen diesen Vorgängen gemeinsam ist und sie zur Sprache, oder zu Teilen der Sprache macht. Du schenkst dir also gerade den Teil der Untersuchung, der dir selbst seinerzeit das meiste Kopfzerbrechen gemacht hat, nämlich den, die ''allgemeine Form des Satzes'' und der Sprache betreffend.« | |||
Und das ist wahr. – Statt etwas anzugeben, was allem, was wir Sprache nennen, gemeinsam ist, sage ich, es ist diesen Erscheinungen gar nicht Eines gemeinsam, weswegen wir für alle das gleiche Wort verwenden, – sondern sie sind miteinander in vielen verschiedenen Weisen ''verwandt''. Und dieser Verwandtschaft, oder dieser Verwandtschaften wegen nennen wir sie alle »Sprachen«. Ich will versuchen, dies zu erklären. | |||
'''66'''. Betrachte z.B. einmal die Vorgänge, die wir »Spiele« nennen. Ich meine Brettspiele, Kartenspiele, Ballspiel, Kampfspiele, usw. Was ist allen diesen gemeinsam? – Sag nicht: »Es ''muß'' ihnen etwas gemeinsam sein, sonst hießen sie nicht ›Spiele‹« – sondern ''schau'', ob ihnen allen etwas gemeinsam ist. – Denn wenn du sie anschaust, wirst du zwar nicht etwas sehen, was ''allen'' gemeinsam wäre, aber du wirst Ähnlichkeiten, Verwandtschaften, sehen, und zwar eine ganze Reihe. Wie gesagt: denk nicht, sondern schau! – Schau z.B. die Brettspiele an, mit ihren mannigfachen Verwandtschaften. Nun geh zu den Kartenspielen über: hier findest du viele Entsprechungen mit jener ersten Klasse, aber viele gemeinsame Züge verschwinden, andere treten auf. Wenn wir nun zu den Ballspielen übergehen, so bleibt manches Gemeinsame erhalten, aber vieles geht verloren. – Sind sie alle ›''unterhaltend''‹. Vergleiche Schach mit dem Mühlfahren. Oder gibt es überall ein Gewinnen und Verlieren, oder eine Konkurrenz der Spielenden? Denk an die Patiencen. In den Ballspielen gibt es Gewinnen und Verlieren; aber wenn ein Kind den Ball an die Wand wirft und wieder auffängt, so ist dieser Zug verschwunden. Schau, welche Rolle Geschick und Glück spielen. Und wie verschieden ist Geschick im Schachspiel und Geschick im Tennisspiel. Denk nun an die Reigenspiele: Hier ist das Element der Unterhaltung, aber wie viele der anderen Charakterzüge sind verschwunden! Und so können wir durch die vielen, vielen anderen Gruppen von Spielen gehen. Ähnlichkeiten auftauchen und verschwinden sehen. | |||
Und das Ergebnis dieser Betrachtung lautet nun: Wir sehen ein kompliziertes Netz von Ähnlichkeiten, die einander übergreifen und kreuzen. Ähnlichkeiten im Großen und Kleinen. | |||
'''67'''. Ich kann diese Ähnlichkeiten nicht besser charakterisieren als durch das Wort »Familienähnlichkeiten«; denn so übergreifen und kreuzen sich die verschiedenen Ähnlichkeiten, die zwischen den Gliedern einer Familie bestehen: Wuchs, Gesichtszüge, Augenfarbe, Gang, Temperament, etc. etc. – Und ich werde sagen: die ›Spiele‹ bilden eine Familie. | |||
Und ebenso bilden z.B. die Zahlenarten eine Familie. Warum nennen wir etwas »Zahl«? Nun etwa, weil es eine – direkte – Verwandtschaft mit manchem hat, was man bisher Zahl genannt hat; und dadurch, kann man sagen, erhält es eine indirekte Verwandtschaft zu anderem, was wir auch ''so'' nennen. Und wir dehnen unseren Begriff der Zahl aus, wie wir beim Spinnen eines Fadens Faser an Faser drehen. Und die Stärke des Fadens liegt nicht darin, daß irgend eine Faser durch seine ganze Länge läuft, sondern darin, daß viele Fasern einander übergreifen. | |||
Wenn aber Einer sagen wollte: »Also ist allen diesen Gebilden etwas gemeinsam, – nämlich die Disjunktion aller dieser Gemeinsamkeiten« – so würde ich antworten: hier spielst du nur mit einem Wort. Ebenso könnte man sagen: es läuft ein Etwas durch den ganzen Faden, – nämlich das lückenlose Übergreifen dieser Fasern. | |||
'''68'''. »Gut; so ist also der Begriff der Zahl für dich erklärt als die logische Summe jener einzelnen miteinander verwandten Begriffe: Kardinalzahl, Rationalzahl, reelle Zahl, etc., und gleicherweise der Begriff des Spiels als logische Summe entsprechender Teilbegriffe.« –– Dies muß nicht sein. Denn ich ''kann'' so dem Begriff ›Zahl‹ feste Grenzen geben, d.h. das Wort »Zahl« zur Bezeichnung eines fest begrenzten Begriffs gebrauchen, aber ich kann es auch so gebrauchen, daß der Umfang des Begriffs ''nicht'' durch eine Grenze abgeschlossen ist. Und so verwenden wir ja das Wort »Spiel«. Wie ist denn der Begriff des Spiels abgeschlossen? Was ist noch ein Spiel und was ist keines mehr? Kannst du die Grenzen angeben? Nein. Du kannst welche ''ziehen'': denn es sind noch keine gezogen. (Aber das hat dich noch nie gestört, wenn du das Wort »Spiel« angewendet hast.) | |||
»Aber dann ist ja die Anwendung des Wortes nicht geregelt; das ›Spiel‹, welches wir mit ihm spielen, ist nicht geregelt.« –– Es ist nicht überall von Regeln begrenzt; aber es gibt ja auch keine Regel dafür z.B., wie hoch man im Tennis den Ball werfen darf, oder wie stark, aber Tennis ist doch ein Spiel und es hat auch Regeln. | |||
'''69'''. Wie würden wir denn jemandem erklären, was ein Spiel ist? Ich glaube, wir werden ihm ''Spiele'' beschreiben, und wir könnten der Beschreibung hinzufügen: »das, ''und Ähnliches'', nennt man ›Spiele‹«. Und wissen wir selbst denn mehr? Können wir etwa nur dem Andern nicht genau sagen, was ein Spiel ist? – Aber das ist nicht Unwissenheit. Wir kennen die Grenzen nicht, weil keine gezogen sind. Wie gesagt, wir können – für einen besondern Zweck – eine Grenze ziehen. Machen wir dadurch den Begriff erst brauchbar? Durchaus nicht! Es sei denn, für diesen besondern Zweck. So wenig, wie der das Längenmaß ›1 Schritt‹ brauchbar machte, der die Definition gab: 1 Schritt = 75 cm. Und wenn du sagen willst »Aber vorher war es doch kein exaktes Längenmaß«, so antworte ich: gut, dann war es ein unexaktes. – Obgleich du mir noch die Definition der Exaktheit schuldig bist. | |||
'''70'''. »Aber wenn der Begriff ›Spiel‹ auf diese Weise unbegrenzt ist, so weißt du ja eigentlich nicht, was du mit ›Spiel‹ meinst.« –– Wenn ich die Beschreibung gebe: »Der Boden war ganz mit Pflanzen bedeckt«, – willst du sagen, ich weiß nicht, wovon ich rede, ehe ich nicht eine Definition der Pflanze geben kann? | |||
Eine Erklärung dessen, was ich meine, wäre etwa eine Zeichnung und die Worte »So ungefähr hat der Boden ausgesehen«. Ich sage vielleicht auch: »''genau'' so hat er ausgesehen«. – Also waren genau ''diese'' Gräser und Blätter, in diesen Lagen, dort? Nein, das heißt es nicht. Und kein Bild würde ich, in ''diesem'' Sinne, als das genaue anerkennen. | |||
<nowiki>##</nowiki> | |||
Jemand sagt mir: »Zeige den Kindern ein Spiel!« Ich lehre sie, um Geld würfeln, und der Andere sagt mir »Ich habe nicht so ein Spiel gemeint«. Mußte ihm da, als er mir den Befehl gab, der Ausschluß des Würfelspiels vorschweben? | |||
<nowiki>##</nowiki> | |||
'''71'''. Man kann sagen, der Begriff ›Spiel‹ ist ein Begriff mit verschwommenen Rändern. – »Aber ist ein verschwommener Begriff überhaupt ein ''Begriff''?« – Ist eine unscharfe Photographie überhaupt ein Bild eines Menschen? Ja, kann man ein unscharfes Bild immer mit Vorteil durch ein scharfes ersetzen? Ist das unscharfe nicht oft gerade das, was wir brauchen? | |||
Frege vergleicht den Begriff mit einem Bezirk und sagt: einen unklar begrenzten Bezirk könne man überhaupt keinen Bezirk nennen. Das heißt wohl, wir können mit ihm nichts anfangen. – Aber ist es sinnlos zu sagen: »Halte dich ungefähr hier auf«? Denk dir, ich stünde mit einem Andern auf einem Platz und sagte dies. Dabei werde ich nicht einmal irgend eine Grenze ziehen, sondern etwa mit der Hand eine zeigende Bewegung machen – als zeigte ich ihm einen bestimmten ''Punkt''. Und gerade so erklärt man etwa, was ein Spiel ist. Man gibt Beispiele und will, daß sie in einem gewissen Sinn verstanden werden. – Aber mit diesem Ausdruck meine ich nicht: er solle nun in diesen Beispielen das Gemeinsame sehen, welches ich – aus irgend einem Grunde – nicht aussprechen konnte. Sondern: er solle diese Beispiele nun in bestimmter Weise ''verwenden''. Das Exemplifizieren ist hier nicht ein ''indirektes'' Mittel der Erklärung, – in Ermanglung eines Bessern. Denn, mißverstanden kann auch jede allgemeine Erklärung werden. ''So'' spielen wir eben das Spiel. (Ich meine das Sprachspiel mit dem Wort »Spiel«.) | |||
'''72'''. ''Das Gemeinsame sehen''. Nimm an, ich zeige jemand verschiedene bunte Bilder, und sage: »Die Farbe, die du in allen siehst, heißt ›Ocker‹.« – Das ist eine Erklärung, die verstanden wird, indem der Andere aufsucht und sieht, was jenen Bildern gemeinsam ist. Er kann dann auf das Gemeinsame blicken, darauf zeigen. | |||
Vergleiche damit: Ich zeige ihm Figuren verschiedener Form, alle in der gleichen Farbe gemalt und sage: »Was diese miteinander gemein haben, heißt ›Ocker‹«. | |||
Und vergleiche damit: Ich zeige ihm Muster verschiedener Schattierungen von Blau und sage: »Die Farbe, die allen gemeinsam ist, nenne ich ›Blau‹«. | |||
'''73'''. Wenn Einer mir den Namen der Farben erklärt, indem er auf Muster zeigt und sagt »Diese Farbe heißt ›Blau‹, diese ›Grün‹,...«, so kann dieser Fall in vieler Hinsicht dem verglichen werden, daß er mir eine Tabelle an die Hand gibt, in der unter den Mustern von Farben die Wörter stehen. – Wenn auch dieser Vergleich in mancher Weise irreführen kann. – Man ist nun geneigt, den Vergleich auszudehnen: Die Erklärung verstanden haben, heißt, einen Begriff des Erklärten im Geiste besitzen, und d.i. ein Muster, oder Bild. Zeigt man mir nun verschiedene Blätter und sagt: »Das nennt man ›Blatt‹«, so erhalte ich einen Begriff der Blattform, ein Bild von ihr im Geiste. – Aber wie schaut denn das Bild eines Blattes aus, das keine bestimmte Form zeigt, sondern ›das, was allen Blattformen gemeinsam ist‹? Welchen Farbton hat das ›Muster in meinem Geiste‹ der Farbe Grün – dessen, was allen Tönen von Grün gemeinsam ist? | |||
»Aber könnte es nicht solche ›allgemeine‹ Muster geben? Etwa ein Blattschema, oder ein Muster von ''reinem'' Grün?« – Gewiß! Aber, daß dieses Schema als ''Schema'' verstanden wird, und nicht als die Form eines bestimmten Blattes, und daß ein Täfelchen von reinem Grün als Muster alles dessen verstanden wird, was grünlich ist, und nicht als Muster für reines Grün – das liegt wieder in der Art der Anwendung dieser Muster. | |||
Frage dich: Welche ''Gestalt'' muß das Muster der Farbe Grün haben? Soll es viereckig sein? oder würde es dann das Muster für grüne Vierecke sein? – Soll es also ›unregelmäßig‹ geformt sein? Und was verhindert uns, es dann nur als Muster der unregelmäßigen Form anzusehen – d.h. zu verwenden? | |||
'''74'''. Hierher gehört auch der Gedanke, daß der, welcher dieses Blatt als Muster ›der Blattform im allgemeinem‹ ansieht, es anders ''sieht'' als der, welcher es etwa als Muster für diese bestimmte Form betrachtet. Nun, das könnte ja so sein – obwohl es nicht so ist – , denn es würde nur besagen, daß erfahrungsgemäß der, welcher das Blatt in bestimmter Weise ''sieht'', es dann so und so, oder den und den Regeln gemäß, verwendet. Es gibt natürlich ein ''so'' und ''anders'' Sehen; und es gibt auch Fälle, in denen der, der ein Muster ''so'' sieht, es im allgemeinen in ''dieser'' Weise verwenden wird, und wer es anders sieht, in anderer Weise. Wer, z.B., die schematische Zeichnung eines Würfels als ebene Figur sieht, bestehend aus einem Quadrat und zwei Rhomben, der wird den Befehl »Bringe mir so etwas!« vielleicht anders ausführen als der, welcher das Bild räumlich sieht. | |||
'''75'''. Was heißt es: wissen, was ein Spiel ist? Was heißt es, es wissen und es nicht sagen können? Ist dieses Wissen irgendein Äquivalent einer nicht ausgesprochenen Definition? So daß, wenn sie ausgesprochen würde, ich sie als den Ausdruck meines Wissens anerkennen könnte? Ist nicht mein Wissen, mein Begriff vom Spiel, ganz in den Erklärungen ausgedrückt, die ich geben könnte? Nämlich darin, daß ich Beispiele von Spielen verschiedener Art beschreibe; zeige, wie man nach Analogie dieser auf alle möglichen Arten andere Spiele konstruieren kann; sage, daß ich das und das wohl kaum mehr ein Spiel nennen würde; und dergleichen mehr. | |||
'''76'''. Wenn Einer eine scharfe Grenze zöge, so könnte ich sie nicht als die anerkennen, die ich auch schon immer ziehen wollte, oder im Geist gezogen habe. Denn ich wollte gar keine ziehen. Man kann dann sagen: sein Begriff ist nicht der gleiche wie der meine, aber ihm verwandt. Und die Verwandtschaft ist die zweier Bilder, deren eines aus unscharf begrenzten Farbflecken, das andere aus ähnlich geformten und verteilten, aber scharf begrenzten, besteht. Die Verwandtschaft ist dann ebenso unleugbar wie die Verschiedenheit. | |||
'''77'''. Und wenn wir diesen Vergleich noch etwas weiter führen, so ist es klar, daß der Grad, bis zu welchem das scharfe Bild dem verschwommenen ähnlich sein ''kann'', vom Grade der Unschärfe des zweiten abhängt. Denn denk dir, du solltest zu einem verschwommenen Bild ein ihm ›entsprechendes‹ scharfes entwerfen. In jenem ist ein unscharfes rotes Rechteck; du setzt dafür ein scharfes. Freilich – es ließen sich ja mehrere solche scharfe Rechtecke ziehen, die dem unscharfen entsprächen. – Wenn aber im Original die Farben ohne die Spur einer Grenze ineinanderfließen, – wird es dann nicht eine hoffnungslose Aufgabe werden, ein dem verschwommenen entsprechendes scharfes Bild zu zeichnen? Wirst du dann nicht sagen müssen: »Hier könnte ich ebenso gut einen Kreis wie ein Rechteck oder eine Herzform zeichnen; es fließen ja alle Farben durcheinander. Es stimmt alles; und nichts.« – Und in dieser Lage befindet sich z.B. der, der in der Ästhetik oder Ethik nach Definitionen sucht, die unseren Begriffen entsprechen. | |||
Frage dich in dieser Schwierigkeit immer: Wie haben wir denn die Bedeutung dieses Wortes (»gut« z.B.) ''gelernt''? An was für Beispielen; in welchen Sprachspielen? (Du wirst dann leichter sehen, daß das Wort eine Familie von Bedeutungen haben muß.) | |||
'''78'''. Vergleiche: ''wissen'' und ''sagen'': | |||
wieviele m hoch der Mont-Blanc ist – | |||
wie das Wort »Spiel« gebraucht wird – | |||
wie eine Klarinette klingt. | |||
Wer sich wundert, daß man etwas wissen könne, und nicht sagen, denkt vielleicht an einen Fall wie den ersten. Gewiß nicht an einen wie den dritten. | |||
'''79'''. Betrachte dieses Beispiel: Wenn man sagt »Moses hat nicht existiert«, so kann das Verschiedenerlei bedeuten. Es kann heißen: die Israeliten haben nicht ''einen'' Führer gehabt, als sie aus Ägypten auszogen –– oder: ihr Führer hat nicht Moses geheißen –– oder: es hat keinen Menschen gegeben, der alles das vollbracht hat, was die Bibel von Moses berichtet –– oder etc. etc. – Nach Russell können wir sagen: der Name »Moses« kann durch verschiedene Beschreibungen definiert werden. Z.B. als: »der Mann, welcher die Israeliten durch die Wüste geführt hat«, »der Mann, welcher zu dieser Zeit und an diesem Ort gelebt hat und damals ›Moses‹ genannt wurde«, »der Mann, welcher als Kind von der Tochter Pharaos aus dem Nil gezogen wurde«, etc. Und je nachdem wir die eine oder die andere Definition annehmen, bekommt der Satz »Moses hat existiert« einen andern Sinn, und ebenso jeder andere Satz, der von Moses handelt. – Und wenn man uns sagt »N hat nicht existiert«, fragen wir auch: »Was meinst du? Willst du sagen, daß ...., oder daß .…, etc.?« | |||
Aber wenn ich nun eine Aussage über Moses mache, – bin ich immer bereit, irgend ''eine'' dieser Beschreibungen für »Moses« zu setzen? Ich werde etwa sagen: Unter »Moses« verstehe ich den Mann, der getan hat, was die Bibel von Moses berichtet, oder doch vieles davon. Aber wievieles? Habe ich mich entschieden, wieviel sich als falsch erweisen muß, damit ich meinen Satz als falsch aufgebe? Hat also der Name »Moses« für mich einen festen und eindeutig bestimmten Gebrauch in allen möglichen Fällen? – Ist es nicht so, daß ich sozusagen eine ganze Reihe von Stützen in Bereitschaft habe und bereit bin, mich auf eine zu stützen, wenn mir die andere entzogen werden sollte, und umgekehrt? –– Betrachte noch einen andern Fall. Wenn ich sage »N ist gestorben«, so kann es mit der Bedeutung des Namens »N« etwa diese Bewandtnis haben: Ich glaube, daß ein Mensch gelebt hat, den ich (1) dort und dort gesehen habe, der (2) so und so ausgeschaut hat (Bilder), (3) das und das getan hat und (4) in der bürgerlichen Welt diesen Namen »N« führt. – Gefragt, was ich unter »N« verstehe, würde ich alles das, oder einiges davon, und bei verschiedenen Gelegenheiten Verschiedenes, aufzählen. Meine Definition von »N« wäre also etwa: »der Mann, von dem alles das stimmt«. – Aber wenn sich nun etwas davon als falsch erwiese! – Werde ich bereit sein, den Satz »N ist gestorben« für falsch zu erklären, – auch wenn nur etwas mir nebensächlich Scheinendes sich als falsch herausstellt? Wo aber ist die Grenze des Nebensächlichen? – Hätte ich in so einem Fall eine Erklärung des Namens gegeben, so wäre ich nun bereit, sie abzuändern. | |||
Und das kann man so ausdrücken: Ich gebrauche den Namen »N« ohne ''feste'' Bedeutung. (Aber das tut seinem Gebrauch so wenig Eintrag, wie dem eines Tisches, daß er auf vier Beinen ruht, statt auf dreien, und daher unter Umständen wackelt.) | |||
Soll man sagen, ich gebrauche ein Wort, dessen Bedeutung ich nicht kenne, rede also Unsinn? – Sage, was du willst, solange dich das nicht verhindert, zu sehen, wie es sich verhält. (Und wenn du das siehst, wirst du manches nicht sagen.) | |||
(Das Schwanken wissenschaftlicher Definitionen: Was heute als erfahrungsmäßige Begleiterscheinung des Phänomens A gilt, wird morgen zur Definition von »A« benützt.) | |||
'''80'''. Ich sage: »Dort steht ein Sessel«. Wie, wenn ich hingehe und ihn holen will, und er entschwindet plötzlich meinem Blick? –– »Also war es kein Sessel, sondern irgend eine Täuschung.« –– Aber in ein paar Sekunden sehen wir ihn wieder und können ihn angreifen, etc. –– »Also war der Sessel doch da und sein Verschwinden war irgend eine Täuschung.« –– Aber nimm an, nach einer Zeit verschwindet er wieder, – oder scheint zu verschwinden. Was sollen wir nun sagen? Hast du für solche Fälle Regeln bereit, – die sagen, ob man so etwas noch »Sessel« nennen darf? Aber gehen sie uns beim Gebrauch des Wortes »Sessel« ab; und sollen wir sagen, daß wir mit diesem Wort eigentlich keine Bedeutung verbinden, da wir nicht für alle Möglichkeiten seiner Anwendung mit Regeln ausgerüstet sind? | |||
'''81'''. F. P. Ramsey hat einmal im Gespräch mit mir betont, die Logik sei eine ›normative Wissenschaft‹. Genau welche Idee ihm dabei vorschwebte, weiß ich nicht; sie war aber zweifellos eng verwandt mit der, die mir erst später aufgegangen ist: daß wir nämlich in der Philosophie den Gebrauch der Wörter oft mit Spielen, Kalkülen nach festen Regeln, ''vergleichen'', aber nicht sagen können, wer die Sprache gebraucht, ''müsse'' ein solches Spiel spielen. – – Sagt man nun aber, daß unser sprachlicher Ausdruck sich solchen Kalkülen ''nur nähert'', so steht man damit unmittelbar am Rande eines Mißverständnisses. Denn so kann es scheinen, als redeten wir in der Logik von einer ''idealen'' Sprache. Als wäre unsre Logik eine Logik, gleichsam, für den luftleeren Raum. – Während die Logik doch nicht von der Sprache – bzw. vom Denken – handelt in dem Sinne, wie eine Naturwissenschaft von einer Naturerscheinung, und man höchstens sagen kann, wir ''konstruierten'' ideale Sprachen. Aber hier wäre das Wort »ideal« irreführend, denn das klingt, als wären diese Sprachen besser, vollkommener, als unsere Umgangssprache; und als brauchte es den Logiker, damit er den Menschen endlich zeigt, wie ein richtiger Satz ausschaut. | |||
All das kann aber erst dann im rechten Licht erscheinen, wenn man über die Begriffe des Verstehens, Meinens und Denkens größere Klarheit gewonnen hat. Denn dann wird es auch klar werden, was uns dazu verleiten kann (und mich verleitet hat) zu denken, daß, wer einen Satz ausspricht und ihn ''meint'', oder ''versteht'', damit einen Kalkül betreibt nach bestimmten Regeln. | |||
'''82'''. Was nenne ich ›die Regel, nach der er vorgehe‹? – Die Hypothese, die seinen Gebrauch der Worte, den wir beobachten, zufriedenstellend beschreibt; oder die Regel, die er beim Gebrauch der Zeichen nachschlägt; oder, die er uns zur Antwort gibt, wenn wir ihn nach seiner Regel fragen? – Wie aber, wenn die Beobachtung keine Regel klar erkennen läßt, und die Frage keine zu Tage fördert? – Denn er gab mir zwar auf meine Frage, was er unter »N« verstehe, eine Erklärung, war aber bereit, diese Erklärung zu widerrufen und abzuändern. – Wie soll ich also die Regel bestimmen, nach der er spielt? Er weiß sie selbst nicht. – Oder richtiger: Was soll der Ausdruck »Regel, nach welcher er vorgeht« hier noch besagen? | |||
'''83'''. Steckt uns da nicht die Analogie der Sprache mit dem Spiel ein Licht auf? Wir können uns doch sehr wohl denken, daß sich Menschen auf einer Wiese damit unterhielten, mit einem Ball zu spielen, so zwar, daß sie verschiedene bestehende Spiele anfingen, manche nicht zu Ende spielten, dazwischen den Ball planlos in die Höhe würfen, einander im Scherz mit dem Ball nachjagen und bewerfen, etc. Und nun sagt Einer: Die ganze Zeit hindurch spielen die Leute ein Ballspiel, und richten sich daher bei jedem Wurf nach bestimmten Regeln. | |||
Und gibt es nicht auch den Fall, wo wir spielen und – ›make up the rules as we go along‹? Ja auch den, in welchem wir sie abandern – as we go along. | |||
'''84'''. Ich sagte von der Anwendung eines Wortes: sie sei nicht überall von Regeln begrenzt. Aber wie schaut denn ein Spiel aus, das überall von Regeln begrenzt ist? dessen Regeln keinen Zweifel eindringen lassen; ihm alle Löcher verstopfen. – Können wir uns nicht eine Regel denken, die die Anwendung der Regel regelt? Und einen Zweifel, den ''jene'' Regel behebt – und so fort? | |||
Aber das sagt nicht, daß wir zweifeln, weil wir uns einen Zweifel ''denken'' können. Ich kann mir sehr wohl denken, daß jemand jedesmal vor dem Öffnen seiner Haustür zweifelt, ob sich hinter ihr nicht ein Abgrund aufgetan hat, und daß er sich darüber vergewissert, eh’ er durch die Tür tritt (und es kann sich einmal erweisen, daß er recht hatte) – aber deswegen zweifle ich im gleichen Falle doch nicht. | |||
'''85'''. Eine Regel steht da, wie ein Wegweiser. – Läßt er keinen Zweifel offen über den Weg, den ich zu gehen habe? Zeigt er, in welche Richtung ich gehen soll, wenn ich an ihm vorbei bin; ob der Straße nach, oder dem Feldweg, oder querfeldein? Aber wo steht, in welchem Sinne ich ihm zu folgen habe; ob in der Richtung der Hand, oder (z.B.) in der entgegengesetzten? – Und wenn statt eines Wegweisers eine geschlossene Kette von Wegweisern stünde, oder Kreidestriche auf dem Boden liefen, – gibt es für sie nur ''eine'' Deutung? – Also kann ich sagen, der Wegweiser läßt doch keinen Zweifel offen. Oder vielmehr: er läßt manchmal einen Zweifel offen, manchmal nicht. Und dies ist nun kein philosophischer Satz mehr, sondern ein Erfahrungssatz. | |||
'''86'''. Ein Sprachspiel wie (2) werde mit Hilfe einer Tabelle gespielt. Die Zeichen, die A dem B gibt, seien nun Schriftzeichen. B hat eine Tabelle; in der ersten Spalte stehen die Schriftzeichen, die im Spiel gebraucht werden, in der zweiten, Bilder von Bausteinformen. A zeigt dem B ein solches Schriftzeichen; B sucht es in der Tabelle auf, blickt auf das gegenüberliegende Bild, etc. Die Tabelle ist also eine Regel, nach der er sich beim Ausführen der Befehle richtet. – Das Aufsuchen des Bildes in der Tabelle lernt man durch Abrichtung, und ein Teil dieser Abrichtung besteht etwa darin, daß der Schüler lernt, in der Tabelle mit dem Finger horizontal von links nach rechts zu fahren; also lernt, sozusagen eine Reihe horizontaler Striche zu ziehen. | |||
Denk dir, es würden nun verschiedene Arten eingeführt eine Tabelle zu lesen; nämlich einmal, wie oben, nach dem Schema: | |||
[[File:Par. 86a.png|250px|center|link=]] | |||
ein andermal nach diesem Schema: | |||
[[File:Par. 86b.png|250px|center|link=]] | |||
oder einem andern. – So ein Schema werde der Tabelle beigefügt als Regel, wie sie zu gebrauchen sei. | |||
Können wir uns nun nicht weitere Regeln zur Erklärung ''dieser'' vorstellen? und war anderseits jene erste Tabelle unvollständig ohne das Schema der Pfeile? Und sind es die andern Tabellen ohne ihr Schema? | |||
'''87'''. Nimm an, ich erkläre: »Unter ›Moses‹ verstehe ich den Mann, wenn es einen solchen gegeben hat, der die Israeliten aus Ägypten geführt hat, wie immer er damals geheißen hat und was immer er sonst getan, oder nicht getan haben mag«. – Aber über die Wörter dieser Erklärung sind ähnliche Zweifel möglich wie die über den Namen »Moses« (was nennst du »Ägypten«, wen »die Israeliten«, etc.?). Ja, diese Fragen kommen auch nicht zu einem Ende, wenn wir bei Wörtern wie »rot«, »dunkel«, »süß«, angelangt wären. – »Aber wie hilft mir dann eine Erklärung zum Verständnis, wenn sie doch nicht die letzte ist? Die Erklärung ist dann ja nie beendet; ich verstehe also noch immer nicht, und nie, was er meint!« – Als hinge eine Erklärung, gleichsam, in der Luft, wenn nicht eine andere sie stütze. Während eine Erklärung zwar auf einer andern, die man gegeben hat, ruhen kann, aber keine einer anderen bedarf – es sei denn, daß ''wir'' sie benötigen, um ein Mißverständnis zu vermeiden. Man könnte sagen: Eine Erklärung dient dazu, ein Mißverständnis zu beseitigen, oder zu verhüten –– also eines, das ohne die Erklärung eintreten würde; aber nicht: jedes, welches ich mir vorstellen kann. | |||
Es kann leicht so scheinen, als ''zeigte'' jeder Zweifel nur eine vorhandene Lücke im Fundament; so daß ein sicheres Verständnis nur dann möglich ist, wenn wir zuerst an allem zweifeln, woran gezweifelt werden ''kann'', und dann alle diese Zweifel beheben. | |||
Der Wegweiser ist in Ordnung, – wenn er, unter normalen Verhältnissen, seinen Zweck erfüllt. | |||
'''88'''. Wenn ich Einem sage »Halte dich ungefähr hier auf!« – kann denn diese Erklärung nicht vollkommen funktionieren? Und kann jede andere nicht auch versagen? | |||
»Aber ist die Erklärung nicht doch unexakt?« – Doch; warum soll man sie nicht »unexakt« nennen? Verstehen wir aber nur, was »unexakt« bedeutet! Denn es bedeutet nun nicht »unbrauchbar«. Und überlegen wir uns doch, was wir, im Gegensatz zu dieser Erklärung, eine »exakte« Erklärung nennen! Etwa das Abgrenzen eines Bezirks durch einen Kreidestrich? Da fällt uns gleich ein, daß der Strich eine Breite hat. Exakter wäre also eine Farbgrenze. Aber hat denn diese Exaktheit hier noch eine Funktion; läuft sie nicht leer? Und wir haben ja auch noch nicht bestimmt, was als Überschreiten dieser scharfen Grenze gelten soll; wie, mit welchen Instrumenten, es festzustellen ist. Usw. | |||
Wir verstehen, was es heißt: eine Taschenuhr auf die genaue Stunde stellen, oder, sie richten, daß sie genau geht. Wie aber, wenn man fragte: Ist diese Genauigkeit eine ideale Genauigkeit, oder wie weit nähert sie sich ihr? – wir können freilich von Zeitmessungen reden, bei welchen es eine andere und, wie wir sagen würden, größere Genauigkeit gibt als bei der Zeitmessung mit der Taschenuhr. Wo die Worte »die Uhr auf die genaue Stunde stellen« eine andere, wenn auch verwandte, Bedeutung haben, und ›die Uhr ablesen‹ ein anderer Vorgang ist, etc. – Wenn ich nun jemandem sage: »Du solltest pünktlicher zum Essen kommen; du weißt, daß es genau um ein Uhr anfängt« – ist hier von ''Genauigkeit'' eigentlich nicht die Rede? weil man sagen kann: »Denk an die Zeitbestimmung im Laboratorium, oder auf der Sternwarte; ''da'' siehst du, was ›Genauigkeit‹ bedeutet.« | |||
»Unexakt«, das ist eigentlich ein Tadel, und »exakt« ein Lob. Und das heißt doch: das Unexakte erreicht sein Ziel nicht so vollkommen wie das Exaktere. Da kommt es also auf das an, was wir »das Ziel« nennen. Ist es unexakt, wenn ich den Abstand der Sonne von uns nicht auf 1 m genau angebe; und dem Tischler die Breite des Tisches nicht auf 0,001 mm? | |||
''Ein'' Ideal der Genauigkeit ist nicht vorgesehen; wir wissen nicht, was wir uns darunter vorstellen sollen – es sei denn, du selbst setzt fest, was so genannt werden soll. Aber es wird dir schwer werden, so eine Festsetzung zu treffen; eine, die dich befriedigt. | |||
'''89'''. Wir stehen mit diesen Überlegungen an dem Ort, wo das Problem steht: Inwiefern ist die Logik etwas Sublimes? | |||
Denn es schien, daß ihr eine besondere Tiefe – allgemeine Bedeutung – zukomme. Sie liege, so schien es, am Grunde aller Wissenschaften. – Denn die logische Betrachtung erforscht das Wesen aller Dinge. Sie will den Dingen auf den Grund sehen, und soll sich nicht um das So oder So des tatsächlichen Geschehens kümmern. –– Sie entspringt nicht einem Interesse für Tatsachen des Naturgeschehens, noch dem Bedürfnisse, kausale Zusammenhänge zu erfassen, sondern einem Streben, das Fundament, oder Wesen, alles Erfahrungsmäßigen zu verstehen. Nicht aber, als sollten wir dazu neue Tatsachen aufspüren: es ist vielmehr für unsere Untersuchung wesentlich, daß wir nichts ''Neues'' mit ihr lernen wollen. Wir wollen etwas ''verstehen'', was schon offen vor unsern Augen liegt. Denn ''das'' scheinen wir, in irgendeinem Sinne, nicht zu verstehen. | |||
Augustinus (Conf. XI/14): »quid est ergo tempus? si nemo ex me quaerat scio; si quaerenti explicare velim, nescio.« – Dies könnte man nicht von einer Frage der Naturwissenschaft sagen (etwa der nach dem spezifischen Gewicht des Wasserstoffs). Das, was man weiß, wenn uns niemand fragt, aber nicht mehr weiß, wenn wir es erklären sollen, ist etwas, worauf man sich ''besinnen'' muß. (Und offenbar etwas, worauf man sich aus irgendeinem Grunde schwer besinnt.) | |||
'''90'''. Es ist uns, als müßten wir die Erscheinungen ''durchschauen'': unsere Untersuchung aber richtet sich nicht auf die ''Erscheinungen'', sondern, wie man sagen könnte, auf die ›''Möglichkeiten''‹ der Erscheinungen. Wir besinnen uns, heißt das, auf die ''Art der Aussagen'', die wir über die Erscheinungen machen. Daher besinnt sich auch Augustinus auf die verschiedenen Aussagen, die man über die Dauer von Ereignissen, über ihre Vergangenheit, Gegenwart, oder Zukunft macht. (Dies sind natürlich ''nicht philosophische'' Aussagen über die Zeit, Vergangenheit, Gegenwart und Zukunft.) | |||
Unsere Betrachtung ist daher eine grammatische. Und diese Betrachtung bringt Licht in unser Problem, indem sie Mißverständnisse wegräumt. Mißverständnisse, die den Gebrauch von Worten betreffen; hervorgerufen, unter anderem, durch gewisse Analogien zwischen den Ausdrucksformen in verschiedenen Gebieten unserer Sprache. – Manche von ihnen lassen sich beseitigen, indem man eine Ausdrucksform durch eine andere ersetzt; dies kann man ein »Analysieren« unsrer Ausdrucksformen nennen, denn der Vorgang hat manchmal Ähnlichkeit mit einem Zerlegen. | |||
'''91'''. Nun aber kann es den Anschein gewinnen, als gäbe es so etwas wie eine letzte Analyse unserer Sprachformen, also ''eine'' vollkommen zerlegte Form des Ausdrucks. D.h.: als seien unsere gebräuchlichen Ausdrucksformen, wesentlich, noch unanalysiert; als sei in ihnen etwas verborgen, was ans Licht zu befördern ist. Ist dies geschehen, so sei der Ausdruck damit vollkommen geklärt und unsre Aufgabe gelöst. | |||
Man kann das auch so sagen: Wir beseitigen Mißverständnisse, indem wir unsern Ausdruck exakter machen: aber es kann nun so scheinen, als ob wir einem bestimmten Zustand, der vollkommenen Exaktheit, zustreben; und als wäre das das eigentliche Ziel unserer Untersuchung. | |||
'''92'''. Dies drückt sich aus in der Frage nach dem Wesen der Sprache, des Satzes, des Denkens. – Denn wenn wir auch in unsern Untersuchungen das Wesen der Sprache – ihre Funktion, ihren Bau – zu verstehen trachten, so ist es doch nicht ''das'', was diese Frage im Auge hat. Denn sie sieht in dem Wesen nicht etwas, was schon offen zutage liegt und was durch Ordnen ''übersichtlich'' wird. Sondern etwas, was ''unter'' der Oberfläche liegt. Etwas, was im Innern liegt, was wir sehen, wenn wir die Sache durchschauen, und was eine Analyse hervorgraben soll. | |||
›''Das Wesen ist uns verborgen''‹. das ist die Form, die unser Problem nun annimmt. Wir fragen: »''Was ist'' die Sprache?«, »''Was ist'' der Satz?«. Und die Antwort auf diese Fragen ist ein für allemal zu geben; und unabhängig von jeder künftigen Erfahrung. | |||
'''93'''. Einer könnte sagen »Ein Satz, das ist das Alltäglichste von der Welt«, und der Andre: »Ein Satz – das ist etwas sehr Merkwürdiges!« –– Und dieser kann nicht: einfach nachschauen, wie Sätze funktionieren. Weil die Formen unserer Ausdrucksweise, die Sätze und das Denken betreffend, ihm im Wege stehen. | |||
Warum sagen wir, der Satz sei etwas Merkwürdiges? Einerseits, wegen der ungeheuren Bedeutung, die ihm zukommt. (Und das ist richtig.) Anderseits verführt uns diese Bedeutung und ein Mißverstehen der Sprachlogik dazu, daß wir meinen, der Satz müsse etwas Außerordentliches, ja Einzigartiges, leisten. – Durch ein ''Mißverständnis'' erscheint es uns, als ''tue'' der Satz etwas Seltsames. | |||
'''94'''. ›Der Satz, ein merkwürdiges Ding!‹: darin liegt schon die Sublimierung der ganzen Darstellung. Die Tendenz, ein reines Mittelwesen anzunehmen zwischen dem Satz''zeichen'' und den Tatsachen. Oder auch, das Satzzeichen selber reinigen, sublimieren, zu wollen. – Denn, daß es mit gewöhnlichen Dingen zugeht, das zu sehen, verhindern uns auf mannigfache Weise unsere Ausdrucksformen, indem sie uns auf die Jagd nach Chimären schicken. | |||
'''95'''. »Denken muß etwas Einzigartiges sein.« Wenn wir sagen, ''meinen'', daß es sich so und so verhält, so halten wir mit dem, was wir meinen, nicht irgendwo vor der Tatsache: sondern meinen, daß ''das und das – so und so – ist''. – Man kann aber dieses Paradox (welches ja die Form einer Selbstverständlichkeit hat) auch so ausdrücken: Man kann ''denken'', was nicht der Fall ist. | |||
'''96'''. Der besondern Täuschung, die hier gemeint ist, schließen sich, von verschiedenen Seiten, andere an. Das Denken, die Sprache, erscheint uns nun als das einzigartige Korrelat, Bild, der Welt. Die Begriffe: Satz, Sprache, Denken, Welt, stehen in einer Reihe hintereinander, jeder dem andern äquivalent. (Wozu aber sind diese Wörter nun zu brauchen? Es fehlt das Sprachspiel, worin sie anzuwenden sind.) | |||
'''97'''. Das Denken ist mit einem Nimbus umgeben. – Sein Wesen, die Logik, stellt eine Ordnung dar, und zwar die Ordnung a priori der Welt, d.i. die Ordnung der ''Möglichkeiten'', die Welt und Denken gemeinsam sein muß. Diese Ordnung aber, scheint es, muß ''höchst einfach'' sein. Sie ist ''vor'' aller Erfahrung; muß sich durch die ganze Erfahrung hindurchziehen; ihr selbst darf keine erfahrungsmäßige Trübe oder Unsicherheit anhaften. –– Sie muß vielmehr vom reinsten Kristall sein. Dieser Kristall aber erscheint nicht als eine Abstraktion; sondern als etwas Konkretes, ja als das Konkreteste, gleichsam ''Härteste''. (Log. Phil. Abh. 5.5563.) | |||
Wir sind in der Täuschung, das Besondere, Tiefe, das uns Wesentliche unserer Untersuchung liege darin, daß sie das unvergleichliche Wesen der Sprache zu begreifen trachtet. D.i., die Ordnung, die zwischen den Begriffen des Satzes, Wortes, Schließens, der Wahrheit, der Erfahrung, usw. besteht. Diese Ordnung ist eine ''Über''-Ordnung zwischen – sozusagen – ''Über''-Begriffen. Während doch die Worte »Sprache«, »Erfahrung«, »Welt«, wenn sie eine Verwendung haben, eine so niedrige haben müssen, wie die Worte »Tisch«, »Lampe«, »Tür«. | |||
'''98'''. Einerseits ist klar, daß jeder Satz unsrer Sprache ›in Ordnung ist, wie er ist‹. D.h., daß wir nicht ein Ideal ''anstreben'': Als hätten unsere gewöhnlichen, vagen Sätze noch keinen ganz untadelhaften Sinn und eine vollkommene Sprache wäre von uns erst zu konstruieren. – Anderseits scheint es klar: Wo Sinn ist, muß vollkommene Ordnung sein. –– Also muß die vollkommene Ordnung auch im vagsten Satze stecken. | |||
'''99'''. Der Sinn des Satzes – möchte man sagen – kann freilich dies oder das offen lassen, aber der Satz muß doch ''einen'' bestimmten Sinn haben. Ein unbestimmter Sinn, – das wäre eigentlich ''gar kein'' Sinn. – Das ist wie: Eine unscharfe Begrenzung, das ist eigentlich gar keine Begrenzung. Man denkt da etwa so: Wenn ich sage »ich habe den Mann fest im Zimmer eingeschlossen – nur ''eine'' Tür ist offen geblieben« – so habe ich ihn eben gar nicht eingeschlossen. Er ist nur zum Schein eingeschlossen. Man wäre geneigt, hier zu sagen: »also hast du damit gar nichts getan«. Eine Umgrenzung, die ein Loch hat, ist so gut, wie ''gar keine''. – Aber ist das denn wahr? | |||
'''100'''. »Es ist doch kein Spiel, wenn es eine Vagheit ''in den Regeln'' gibt.« – Aber ''ist'' es dann kein Spiel? – »Ja, vielleicht wirst du es Spiel nennen, aber es ist doch jedenfalls kein vollkommenes Spiel.« D.h.: es ist doch dann verunreinigt, und ich interessiere mich nun für dasjenige, was hier verunreinigt wurde. – Aber ich will sagen: Wir mißverstehen die Rolle, die das Ideal in unsrer Ausdrucksweise spielt. D.h.: auch wir würden es ein Spiel nennen, nur sind wir vom Ideal geblendet und sehen daher nicht deutlich die wirkliche Anwendung des Wortes »Spiel«. | |||
Revision as of 08:49, 14 March 2021
Ludwig Wittgenstein
Philosophische Untersuchungen
NESTROY
Vorwort
In dem Folgenden veröffentliche ich Gedanken, den Niederschlag philosophischer Untersuchungen, die mich in den letzten 16 Jahren beschäftigt haben. Sie betreffen viele Gegenstände: Den Begriff der Bedeutung, des Verstehens, des Satzes, der Logik, die Grundlagen der Mathematik, die Bewußtseinszustände und Anderes. Ich habe diese Gedanken alle als Bemerkungen, kurze Absätze, niedergeschrieben. Manchmal in längeren Ketten, über den gleichen Gegenstand, manchmal in raschem Wechsel von einem Gebiet zum andern überspringend. – Meine Absicht war es von Anfang, alles dies einmal in einem Buche zusammenzufassen, von dessen Form ich mir zu verschiedenen Zeiten verschiedene Vorstellungen machte. Wesentlich aber schien es mir, daß darin die Gedanken von einem Gegenstand zum andern in einer natürlichen und lückenlosen Folge fortschreiten sollten.
Nach manchen mißglückten Versuchen, meine Ergebnisse zu einem solchen Ganzen zusammenzuschweißen, sah ich ein, daß mir dies nie gelingen würde. Daß das beste, was ich schreiben konnte, immer nur philosophische Bemerkungen bleiben würden; daß meine Gedanken bald erlahmten, wenn ich versuchte, sie, gegen ihre natürliche Neigung, in einer Richtung weiterzuzwingen. –– Und dies hing freilich mit der Natur der Untersuchung selbst zusammen. Sie nämlich zwingt uns, ein weites Gedankengebiet, kreuz und quer, nach allen Richtungen hin zu durchreisen. –– Die philosophischen Bemerkungen dieses Buches sind gleichsam eine Menge von Landschaftsskizzen, die auf diesen langen und verwickelten Fahrten entstanden sind.
Die gleichen Punkte, oder beinahe die gleichen, wurden stets von neuem von verschiedenen Richtungen her berührt und immer neue Bilder entworfen. Eine Unzahl dieser waren verzeichnet, oder uncharakteristisch, mit allen Mängeln eines schwachen Zeichners behaftet. Und wenn man diese ausschied, blieb eine Anzahl halbwegser übrig, die nun so angeordnet, oftmals beschnitten, werden mußten, daß sie dem Betrachter ein Bild der Landschaft geben konnten. – So ist also dieses Buch eigentlich nur ein Album.
Ich hatte bis vor kurzem den Gedanken an eine Veröffentlichung meiner Arbeit bei meinen Lebzeiten eigentlich aufgegeben. Er wurde allerdings von Zeit zu Zeit rege gemacht, und zwar hauptsächlich dadurch, daß ich erfahren mußte, daß meine Ergebnisse, die ich in Vorlesungen, Skripten und Diskussionen weitergegeben hatte, vielfach mißverstanden, mehr oder weniger verwässert oder verstümmelt im Umlauf waren. Hierdurch wurde meine Eitelkeit aufgestachelt, und ich hatte Mühe, sie zu beruhigen.
Vor zwei Jahren aber hatte ich Veranlassung, mein erstes Buch (die »Logisch-Philosophische Abhandlung«) wieder zu lesen und seine Gedanken zu erklären. Da schien es mir plötzlich, daß ich jene alten Gedanken und die neuen zusammen veröffentlichen sollte: daß diese nur durch den Gegensatz und auf dem Hintergrund meiner älteren Denkweise ihre rechte Beleuchtung erhalten könnten.
Seit ich nämlich vor 16 Jahren mich wieder mit Philosophie zu beschäftigen anfing, mußte ich schwere Irrtümer in dem erkennen, was ich in jenem ersten Buche niedergelegt hatte. Diese Irrtümer einzusehen, hat mir – in einem Maße, das ich kaum selbst zu beurteilen vermag – die Kritik geholfen, die meine Ideen durch Frank Ramsey erfahren haben, – mit welchem ich sie während der zwei letzten Jahre seines Lebens in zahllosen Gesprächen erörtert habe. – Mehr noch als dieser – stets kraftvollen und sichern – Kritik verdanke ich derjenigen, die ein Lehrer dieser Universität, Herr P. Sraffa durch viele Jahre unablässig an meinen Gedanken geübt hat. Diesem Ansporn verdanke ich die folgereichsten der Ideen dieser Schrift.
Aus mehr als einem Grunde wird, was ich hier veröffentliche, sich mit dem berühren, was Andre heute schreiben. – Tragen meine Bemerkungen keinen Stempel an sich, der sie als die meinen kennzeichnet, – so will ich sie auch weiter nicht als mein Eigentum beanspruchen.
Ich übergebe sie mit zweifelhaften Gefühlen der Öffentlichkeit. Daß es dieser Arbeit in ihrer Dürftigkeit und der Finsternis dieser Zeit beschieden sein sollte Licht in ein oder das andere Gehirn zu werfen, ist nicht unmöglich; aber freilich nicht wahrscheinlich.
Ich möchte nicht mit meiner Schrift Andern das Denken ersparen. Sondern, wenn es möglich wäre, jemand zu eigenen Gedanken anregen.
Ich hätte gerne ein gutes Buch hervorgebracht. Es ist nicht so ausgefallen; aber die Zeit ist vorbei, in der es von mir verbessert werden könnte.
Cambridge, im Januar 1945.
1. Augustinus, in den Confessiones I/8: cum ipsi (majores homines) appellabant rem aliquam, et cum secundum eam vocem corpus ad aliquid movebant, videbam, et tenebam hoc ab eis vocari rem illam, quod sonabant, cum eam vellent ostendere. Hoc autem eos velle ex motu corporis aperiebatur: tamquam verbis naturalibus omnium gentium, quae fiunt vultu et nutu oculorum, ceterorumque membrorum actu, et sonitu vocis indicante affectionem animi in petendis, habendis, rejicindis, fugiendisve rebus. Ita verba in variis sententiis locis suis posita, et crebro audita, quarum rerum signa essent, paulatim colligebam, measque iam voluntates, edomito in eis signis ore, per haec enuntiabam.
[Nannten die Erwachsenen irgend einen Gegenstand und wandten sie sich dabei ihm zu, so nahm ich das wahr und ich begriff, daß der Gegenstand durch die Laute, die sie aussprachen, bezeichnet wurde, da sie auf ihn hinweisen wollten. Dies aber entnahm ich aus ihren Gebärden, der natürlichen Sprache aller Völker, der Sprache, die durch Mienen- und Augenspiel, durch die Bewegungen der Glieder und den Klang der Stimme die Empfindungen der Seele anzeigt, wenn diese irgend etwas begehrt, oder festhält, oder zurückweist, oder flieht. So lernte ich nach und nach verstehen, welche Dinge die Wörter bezeichneten, die ich wieder und wieder, an ihren bestimmten Stellen in verschiedenen Sätzen, aussprechen hörte. Und ich brachte, als nun mein Mund sich an diese Zeichen gewöhnt hatte, durch sie meine Wünsche zum Ausdruck.]
In diesen Worten erhalten wir, so scheint es mir, ein bestimmtes Bild von dem Wesen der menschlichen Sprache. Nämlich dieses: Die Wörter der Sprache benennen Gegenstände – Sätze sind Verbindungen von solchen Benennungen. –– In diesem Bild von der Sprache finden wir die Wurzeln der Idee: Jedes Wort hat eine Bedeutung. Diese Bedeutung ist dem Wort zugeordnet. Sie ist der Gegenstand, für welchen das Wort steht.
Von einem Unterschied der Wortarten spricht Augustinus nicht. Wer das Lernen der Sprache so beschreibt, denkt, so möchte ich glauben, zunächst an Hauptwörter, wie »Tisch«, »Stuhl«, »Brot«, und die Namen von Personen, erst in zweiter Linie an die Namen gewisser Tätigkeiten und Eigenschaften, und an die übrigen Wortarten als etwas, was sich finden wird.
Denke nun an diese Verwendung der Sprache: Ich schicke jemand einkaufen. Ich gebe ihm einen Zettel, auf diesem stehen die Zeichen: »fünf rote Äpfel«. Er trägt den Zettel zum Kaufmann; der öffnet die Lade, auf welcher das Zeichen »Äpfel« steht; dann sucht er in einer Tabelle das Wort »rot« auf und findet ihm gegenüber ein Farbmuster; nun sagt er die Reihe der Grundzahlwörter – ich nehme an, er weiß sie auswendig – bis zum Worte »fünf« und bei jedem Zahlwort nimmt er einen Apfel aus der Lade, der die Farbe des Musters hat. –– So, und ähnlich, operiert man mit Worten. –– »Wie weiß er aber, wo und wie er das Wort »rot« nachschlagen soll und was er mit dem Wort »fünf« anzufangen hat?« –– Nun, ich nehme an, er handelt, wie ich es beschrieben habe. Die Erklärungen haben irgendwo ein Ende. – Was ist aber die Bedeutung des Wortes »fünf«? – Von einer solchen war hier gar nicht die Rede; nur davon, wie das Wort »fünf« gebraucht wird.
2. Jener philosophische Begriff der Bedeutung ist in einer primitiven Vorstellung von der Art und Weise, wie die Sprache funktioniert, zu Hause. Man kann aber auch sagen, es sei die Vorstellung einer primitiveren Sprache als der unsern.
Denken wir uns eine Sprache, für die die Beschreibung, wie Augustinus sie gegeben hat, stimmt: Die Sprache soll der Verständigung eines Bauenden A mit einem Gehilfen B dienen. A führt einen Bau auf aus Bausteinen; es sind Würfel, Säulen, Platten und Balken vorhanden. B hat ihm die Bausteine zuzureichen, und zwar nach der Reihe, wie A sie braucht. Zu dem Zweck bedienen sie sich einer Sprache, bestehend aus den Wörtern: »Würfel«, »Säule«, »Platte«, »Balken«. A ruft sie aus; – B bringt den Stein, den er gelernt hat, auf diesen Ruf zu bringen. –– Fasse dies als vollständige primitive Sprache auf.
3. Augustinus beschreibt, könnten wir sagen, ein System der Verständigung; nur ist nicht alles, was wir Sprache nennen, dieses System. Und das muß man in so manchen Fällen sagen, wo sich die Frage erhebt: »Ist diese Darstellung brauchbar, oder unbrauchbar?« Die Antwort ist dann: »Ja, brauchbar; aber nur für dieses eng umschriebene Gebiet, nicht für das Ganze, das du darzustellen vorgabst.«
Es ist, als erklärte jemand: »Spielen besteht darin, daß man Dinge, gewissen Regeln gemäß, auf einer Fläche verschiebt...« – und wir ihm antworten: Du scheinst an die Brettspiele zu denken; aber das sind nicht alle Spiele. Du kannst deine Erklärung richtigstellen, indem du sie ausdrücklich auf diese Spiele einschränkst.
4. Denk dir eine Schrift, in welcher Buchstaben zur Bezeichnung von Lauten benützt würden, aber auch zur Bezeichnung der Betonung und als Interpunktionszeichen. (Eine Schrift kann man auffassen als eine Sprache zur Beschreibung von Lautbildern.) Denk dir nun, daß Einer jene Schrift so verstünde, als entspräche einfach jedem Buchstaben ein Laut und als hätten die Buchstaben nicht auch ganz andere Funktionen. So einer, zu einfachen, Auffassung der Schrift gleicht Augustinus’ Auffassung der Sprache.
5. Wenn man das Beispiel im § 1 betrachtet, so ahnt man vielleicht, inwiefern der allgemeine Begriff der Bedeutung der Worte das Funktionieren der Sprache mit einem Dunst umgibt, der das klare Sehen unmöglich macht. – Es zerstreut den Nebel, wenn wir die Erscheinungen der Sprache an primitiven Arten ihrer Verwendung studieren, in denen man den Zweck und das Funktionieren der Wörter klar übersehen kann.
Solche primitiven Formen der Sprache verwendet das Kind, wenn es sprechen lernt. Das Lehren der Sprache ist hier kein Erklären, sondern ein Abrichten.
6. Wir könnten uns vorstellen, daß die Sprache im § 2 die ganze Sprache des A und B ist; ja, die ganze Sprache eines Volksstamms. Die Kinder werden dazu erzogen, diese Tätigkeiten zu verrichten, diese Wörter dabei zu gebrauchen, und so auf die Worte des Anderen zu reagieren.
Ein wichtiger Teil der Abrichtung wird darin bestehen, daß der Lehrende auf die Gegenstände weist, die Aufmerksamkeit des Kindes auf sie lenkt, und dabei ein Wort ausspricht; z. B. das Wort »Platte« beim Vorzeigen dieser Form. (Dies will ich nicht »hinweisende Erklärung«, oder »Definition«, nennen, weil ja das Kind noch nicht nach der Benennung fragen kann. Ich will es »hinweisendes Lehren der Wörter« nennen. –– Ich sage, es wird einen wichtigen Teil der Abrichtung bilden, weil es bei Menschen so der Fall ist; nicht, weil es sich nicht anders vorstellen ließe.) Dieses hinweisende Lehren der Wörter, kann man sagen, schlägt eine assoziative Verbindung zwischen dem Wort und dem Ding: Aber was heißt das? Nun, es kann Verschiedenes heißen; aber man denkt wohl zunächst daran, daß dem Kind das Bild des Dings vor die Seele tritt, wenn es das Wort hört. Aber wenn das nun geschieht, – ist das der Zweck des Worts? – Ja, es kann der Zweck sein. – Ich kann mir eine solche Verwendung von Wörtern (Lautreihen) denken. (Das Aussprechen eines Wortes ist gleichsam ein Anschlagen einer Taste auf dem Vorstellungsklavier.) Aber in der Sprache im § 2 ist es nicht der Zweck der Wörter, Vorstellungen zu erwecken. (Es kann freilich auch gefunden werden, daß dies dem eigentlichen Zweck förderlich ist.)
Wenn aber das das hinweisende Lehren bewirkt, – soll ich sagen, es bewirkt das Verstehen des Worts ? Versteht nicht der den Ruf »Platte!«, der so und so nach ihm handelt? – Aber dies half wohl das hinweisende Lehren herbeiführen; aber doch nur zusammen mit einem bestimmten Unterricht. Mit einem anderen Unterricht hätte dasselbe hinweisende Lehren dieser Wörter ein ganz anderes Verständnis bewirkt.
»Indem ich die Stange mit dem Hebel verbinde, setze ich die Bremse instand.« – Ja, gegeben den ganzen übrigen Mechanismus. Nur mit diesem ist er der Bremshebel; und losgelöst von seiner Unterstützung ist er nicht einmal Hebel, sondern kann alles Mögliche sein, oder nichts.
7. In der Praxis des Gebrauchs der Sprache (2) ruft der eine Teil die Wörter, der andere handelt nach ihnen; im Unterricht der Sprache aber wird sich dieser Vorgang finden: Der Lernende benennt die Gegenstände. D.h. er spricht das Wort, wenn der Lehrer auf den Stein zeigt. – Ja, es wird sich hier die noch einfachere Übung finden: der Schüler spricht die Worte nach, die der Lehrer ihm vorsagt –– beides sprachähnliche Vorgänge.
Wir können uns auch denken, daß der ganze Vorgang des Gebrauchs der Worte in (2) eines jener Spiele ist, mittels welcher Kinder ihre Muttersprache erlernen. Ich will diese Spiele »Sprachspiele« nennen, und von einer primitiven Sprache manchmal als einem Sprachspiel reden.
Und man könnte die Vorgänge des Benennens der Steine und des Nachsprechens des vorgesagten Wortes auch Sprachspiele nennen. Denke an manchen Gebrauch, der von Worten in Reigenspielen gemacht wird.
Ich werde auch das Ganze: der Sprache und der Tätigkeiten, mit denen sie verwoben ist, das »Sprachspiel« nennen.
8. Sehen wir eine Erweiterung der Sprache (2) an. Außer den vier Wörtern »Würfel«, »Säule«, etc. enthalte sie eine Wörterreihe, die verwendet wird, wie der Kaufmann in (1) die Zahlwörter verwendet (es kann die Reihe der Buchstaben des Alphabets sein); ferner, zwei Wörter, sie mögen »dorthin« und »dieses« lauten (weil dies schon ungefähr ihren Zweck andeutet), sie werden in Verbindung mit einer zeigenden Handbewegung gebraucht; und endlich eine Anzahl von Farbmustern. A gibt einen Befehl von der Art: »d-Platte-dorthin«. Dabei läßt er den Gehilfen ein Farbmuster sehen, und beim Worte »dorthin« zeigt er an eine Stelle des Bauplatzes. B nimmt von dem Vorrat der Platten je eine von der Farbe des Musters für jeden Buchstaben des Alphabets bis zum »d« und bringt sie an den Ort, den A bezeichnet. – Bei anderen Gelegenheiten gibt A den Befehl: »dieses-dorthin«. Bei »dieses« zeigt er auf einen Baustein. Usw.
9. Wenn das Kind diese Sprache lernt, muß es die Reihe der ›Zahlwörter‹ a, b, c, ... auswendiglernen. Und es muß ihren Gebrauch lernen. – Wird in diesem Unterricht auch ein hinweisendes Lehren der Wörter vorkommen? – Nun, es wird z.B. auf Platten gewiesen und gezählt werden: »a, b, c Platten«. – Mehr Ähnlichkeit mit dem hinweisenden Lehren der Wörter »Würfel«, »Säule«, etc. hätte das hinweisende Lehren von Zahlwörtern, die nicht zum Zählen dienen, sondern zur Bezeichnung mit dem Auge erfassbarer Gruppen von Dingen. So lernen ja Kinder den Gebrauch der ersten fünf oder sechs Grundzahlwörter.
Wird auch »dorthin« und »dieses« hinweisend gelehrt? – Stell dir vor, wie man ihren Gebrauch etwa lehren könnte! Es wird dabei auf Örter und Dinge gezeigt werden, – aber hier geschieht ja dieses Zeigen auch im Gebrauch der Wörter und nicht nur beim Lernen des Gebrauchs. –
10. Was bezeichnen nun die Wörter dieser Sprache? – Was sie bezeichnen, wie soll ich das zeigen, es sei denn in der Art ihres Gebrauchs? Und den haben wir ja beschrieben. Der Ausdruck »dieses Wort bezeichnet das« müßte also ein Teil dieser Beschreibung werden. Oder: die Beschreibung soll auf die Form gebracht werden: »Das Wort.... bezeichnet....«.
Nun, man kann ja die Beschreibung des Gebrauchs des Wortes »Platte« dahin abkürzen, daß man sagt, dieses Wort bezeichne diesen Gegenstand. Das wird man tun, wenn es sich z.B. nurmehr darum handelt, das Mißverständnis zu beseitigen, das Wort »Platte« beziehe sich auf die Bausteinform, die wir tatsächlich »Würfel« nennen, – die Art und Weise dieses ›Bezugs‹ aber, d.h. der Gebrauch dieser Worte im übrigen, bekannt ist.
Und ebenso kann man sagen, die Zeichen »a«, »b«, etc. bezeichnen Zahlen; wenn dies etwa das Mißverständnis behebt, »a«, »b«, »c«, spielten in der Sprache die Rolle, die in Wirklichkeit »Würfel«, »Platte«, »Säule«, spielen. Und man kann auch sagen, »c« bezeichne diese Zahl und nicht jene; wenn damit etwa erklärt wird, die Buchstaben seien in der Reihenfolge a, b, c, d, etc. zu verwenden und nicht in der: a, b, d, c.
Aber dadurch, daß man so die Beschreibungen des Gebrauchs der Wörter einander anähnelt, kann doch dieser Gebrauch nicht ähnlicher werden! Denn, wie wir sehen, ist er ganz und gar ungleichartig.
11. Denk an die Werkzeuge in einem Werkzeugkasten: es ist da ein Hammer, eine Zange, eine Säge, ein Schraubenzieher, ein Maßstab, ein Leimtopf, Leim, Nägel und Schrauben. – So verschieden die Funktionen dieser Gegenstände, so verschieden sind die Funktionen der Wörter. (Und es gibt Ähnlichkeiten hier und dort.)
Freilich, was uns verwirrt ist die Gleichförmigkeit ihrer Erscheinung, wenn die Wörter uns gesprochen, oder in der Schrift und im Druck entgegentreten. Denn ihre Verwendung steht nicht so deutlich vor uns. Besonders nicht, wenn wir philosophieren!
12. Wie wenn wir in den Führerstand einer Lokomotive schauen: da sind Handgriffe, die alle mehr oder weniger gleich aussehen. (Das ist begreiflich, denn sie sollen alle mit der Hand angefaßt werden.) Aber einer ist der Handgriff einer Kurbel, die kontinuierlich verstellt werden kann (sie reguliert die Offnung eines Ventils); ein andrer ist der Handgriff eines Schalters, der nur zweierlei wirksame Stellungen hat, er ist entweder umgelegt, oder aufgestellt; ein dritter ist der Griff eines Bremshebels, je stärker man zieht, desto stärker wird gebremst; ein vierter, der Handgriff einer Pumpe, er wirkt nur, solange er hin und her bewegt wird.
13. Wenn wir sagen: »jedes Wort der Sprache bezeichnet etwas« so ist damit vorerst noch gar nichts gesagt; es sei denn, daß wir genau erklärten, welche Unterscheidung wir zu machen wünschen. (Es könnte ja sein, daß wir die Wörter der Sprache (8) von Wörtern ›ohne Bedeutung‹ unterscheiden wollten, wie sie in Gedichten Lewis Carroll’s vorkommen, oder von Worten wie »juwiwallera« in einem Lied.)
14. Denke dir, jemand sagte: »Alle Werkzeuge dienen dazu, etwas zu modifizieren. So, der Hammer die Lage des Nagels, die Säge die Form des Bretts, etc.« – Und was modifiziert der Maßstab, der Leimtopf, die Nägel? – »Unser Wissen um die Länge eines Dings, die Temperatur des Leims, und die Festigkeit der Kiste.« –– Wäre mit dieser Assimilation des Ausdrucks etwas gewonnen? –
15. Am direktesten ist das Wort »bezeichnen« vielleicht da angewandt, wo das Zeichen auf dem Gegenstand steht, den es bezeichnet. Nimm an, die Werkzeuge, die A beim Bauen benützt, tragen gewisse Zeichen. Zeigt A dem Gehilfen ein solches Zeichen, so bringt dieser das Werkzeug, das mit dem Zeichen versehen ist.
So, und auf mehr oder weniger ähnliche Weise, bezeichnet ein Name ein Ding, und wird ein Name einem Ding gegeben. – Es wird sich oft nützlich erweisen, wenn wir uns beim Philosophieren sagen: Etwas benennen, das ist etwas Ähnliches, wie einem Ding ein Namentäfelchen anheften.
16. Wie ist es mit den Farbmustern, die A dem B zeigt, – gehören sie zur Sprache? Nun, wie man will. Zur Wortsprache gehören sie nicht; aber wenn ich jemandem sage: »Sprich das Wort ›das‹ aus«, so wirst du doch dieses zweite »›das‹« auch noch zum Satz rechnen. Und doch spielt es eine ganz ähnliche Rolle, wie ein Farbmuster im Sprachspiel (8); es ist nämlich ein Muster dessen, was der Andre sagen soll.
Es ist das Natürlichste, und richtet am wenigsten Verwirrung an, wenn wir die Muster zu den Werkzeugen der Sprache rechnen.
((Bemerkung über das reflexive Fürwort »dieser Satz«.))
17. Wir werden sagen können: in der Sprache (8) haben wir verschiedene Wortarten. Denn die Funktion des Wortes »Platte« und des Wortes »Würfel« sind einander ähnlicher als die von »Platte« und von »d«. Wie wir aber die Worte nach Arten zusammenfassen, wird vom Zweck der Einteilung abhängen, – und von unserer Neigung.
Denke an die verschiedenen Gesichtspunkte, nach denen man Werkzeuge in Werkzeugarten einteilen kann. Oder Schachfiguren in Figurenarten.
18. Daß die Sprachen (2) und (8) nur aus Befehlen bestehen, laß dich nicht stören. Willst du sagen, sie seien darum nicht vollständig, so frage dich, ob unsere Sprache vollständig ist; – ob sie es war, ehe ihr der chemische Symbolismus und die Infinitesimalnotation einverleibt wurden; denn dies sind, sozusagen, Vorstädte unserer Sprache. (Und mit wieviel Häusern, oder Straßen, fängt eine Stadt an, Stadt zu sein?) Unsere Sprache kann man ansehen als eine alte Stadt: Ein Gewinkel von Gässchen und Plätzen, alten und neuen Häusern, und Häusern mit Zubauten aus verschiedenen Zeiten; und dies umgeben von einer Menge neuer Vororte mit geraden und regelmäßigen Straßen und mit einförmigen Häusern.
19. Man kann sich leicht eine Sprache vorstellen, die nur aus Befehlen und Meldungen in der Schlacht besteht. – Oder eine Sprache, die nur aus Fragen besteht und einem Ausdruck der Bejahung und der Verneinung. Und unzählige Andere. –– Und eine Sprache vorstellen heißt, sich eine Lebensform vorstellen.
Wie ist es aber: Ist der Ruf »Platte!« im Beispiel (2) ein Satz oder ein Wort? – Wenn ein Wort, so hat es doch nicht dieselbe Bedeutung wie das gleichlautende unserer gewöhnlichen Sprache, denn im § 2 ist es ja ein Ruf. Wenn aber ein Satz, so ist es doch nicht der elliptische Satz »Platte!« unserer Sprache. –– Was die erste Frage anbelangt, so kannst du »Platte!« ein Wort, und auch einen Satz nennen; vielleicht treffend einen ›degenerierten Satz‹ (wie man von einer degenerierten Hyperbel spricht), und zwar ist es eben unser ›elliptischer‹ Satz. – Aber der ist doch nur eine verkürzte Form des Satzes »Bring mir eine Platte!« und diesen Satz gibt es doch in Beispiel (2) nicht. – Aber warum sollte ich nicht, umgekehrt, den Satz »Bring mir eine Platte!« eine Verlängerung des Satzes »Platte!« nennen? – Weil der, der »Platte!« ruft, eigentlich meint: »Bring mir eine Platte!«. – Aber wie machst du das, dies meinen, während du »Platte« sagst? Sprichst du dir inwendig den unverkürzten Satz vor? Und warum soll ich, um zu sagen, was Einer mit dem Ruf »Platte« meint, diesen Ausdruck in einen andern übersetzen? Und wenn sie das Gleiche bedeuten, – warum soll ich nicht sagen: »wenn er ›Platte!‹ sagt, meint er ›Platte!‹«? Oder: warum sollst du nicht »Platte« meinen können, wenn du »Bring mir die Platte« meinen kannst? –– Aber wenn ich »Platte!« rufe, so will ich doch, er soll mir eine Platte bringen! –– Gewiß, aber besteht ›dies wollen‹ darin, daß du in irgend einer Form einen andern Satz denkst als den, den du sagst? –
20. Aber wenn nun Einer sagt »Bring mir eine Platte!«, so scheint es ja jetzt, als könnte er diesen Ausdruck als ein langes Wort meinen: entsprechend nämlich dem einen Worte »Platte!«. –– Kann man ihn also einmal als ein Wort, einmal als vier Wörter meinen? Und wie meint man ihn gewöhnlich? –– Ich glaube, wir werden geneigt sein, zu sagen: Wir meinen den Satz als einen von vier Wörtern, wenn wir ihn im Gegensatz zu andern Sätzen gebrauchen, wie »Reich mir eine Platte zu«, »Bring ihm eine Platte«, »Bring zwei Platten«, etc.; also im Gegensatz zu Sätzen, welche die Wörter unseres Befehls in andern Verbindungen enthalten. –– Aber worin besteht es, einen Satz im Gegensatz zu andern Sätzen gebrauchen? Schweben einem dabei etwa diese Sätze vor? Und alle? Und während man den einen Satz sagt, oder vor-, oder nachher? – Nein! Wenn auch so eine Erklärung einige Versuchung für uns hat, so brauchen wir doch nur einen Augenblick zu bedenken, was wirklich geschieht, um zu sehen, daß wir hier auf falschem Weg sind. Wir sagen, wir gebrauchen den Befehl im Gegensatz zu andern Sätzen, weil unsere Sprache die Möglichkeit dieser andern Sätze enthält. Wer unsere Sprache nicht versteht, ein Ausländer, der öfter gehört hätte, wie jemand den Befehl gibt »Bring mir eine Platte!«, könnte der Meinung sein, diese ganze Lautreihe sei ein Wort und entspräche etwa dem Wort für »Baustein« in seiner Sprache. Wenn er selbst dann diesen Befehl gegeben hätte, würde er ihn vielleicht anders aussprechen, und wir würden sagen: Er spricht ihn so sonderbar aus, weil er ihn für ein Wort hält. –– Aber geht also nicht, wenn er ihn ausspricht, eben auch etwas anderes in ihm vor, – dem entsprechend, daß er den Satz als ein Wort auffaßt? –– Es kann das Gleiche in ihm vorgehen, oder auch anderes. Was geht denn in dir vor, wenn du so einen Befehl gibst; bist du dir bewußt, daß er aus vier Wörtern besieht, während du ihn aussprichst? Freilich, du beherrschst diese Sprache – in der es auch jene andern Sätze gibt – aber ist dieses Beherrschen etwas, was ›geschieht‹, während du den Satz aussprichst? – Und ich habe ja zugegeben: der Fremde wird den Satz, den er anders auffaßt, wahrscheinlich anders aussprechen; aber, was wir die falsche Auffassung nennen, muß nicht in irgend etwas liegen, was das Aussprechen des Befehls begleitet.
›Elliptisch‹ ist der Satz nicht, weil er etwas ausläßt, was wir meinen, wenn wir ihn aussprechen, sondern weil er gekürzt ist – im Vergleich mit einem bestimmten Vorbild unserer Grammatik.–Man könnte hier freilich den Einwand machen: »Du gibst zu, daß der verkürzte und der unverkürzte Satz den gleichen Sinn haben. – Welchen Sinn haben sie also? Gibt es denn für diesen Sinn nicht einen Wortausdruck?« –– Aber besteht der gleiche Sinn der Sätze nicht in ihrer gleichen Verwendung? – (Im Russischen heißt es »Stein rot« statt »der Stein ist rot«; geht ihnen die Kopula im Sinn ab, oder denken sie sich die Kopula dazu?)
21. Denke dir ein Sprachspiel, in welchem B dem A auf dessen Frage die Anzahl der Platten, oder Würfel in einem Stoß meldet, oder die Farben und Formen der Bausteine, die dort und dort liegen. – So eine Meldung könnte also lauten: »Fünf Platten«. Was ist nun der Unterschied zwischen der Meldung, oder Behauptung, »Fünf Platten« und dem Befehl »Fünf Platten!«? – Nun, die Rolle, die das Aussprechen dieser Worte im Sprachspiel spielt. Aber es wird wohl auch der Ton, in dem sie ausgesprochen werden, ein anderer sein, und die Miene, und noch manches andere. Aber wir können uns auch denken, daß der Ton der gleiche ist, – denn ein Befehl und eine Meldung können in mancherlei Ton ausgesprochen werden und mit mancherlei Miene – und daß der Unterschied allein in der Verwendung liegt. (Freilich könnten wir auch die Worte »Behauptung« und »Befehl« zur Bezeichnung einer grammatischen Satzform und eines Tonfalls gebrauchen; wie wir ja »Ist das Wetter heute nicht herrlich?« eine Frage nennen, obwohl sie als Behauptung verwendet wird.) Wir könnten uns eine Sprache denken, in der alle Behauptungen die Form und den Ton rhetorischer Fragen hätten; oder jeder Befehl die Form der Frage: »Möchtest du das tun?« Man wird dann vielleicht sagen: »Was er sagt, hat die Form der Frage, ist aber wirklich ein Befehl« – d.h., hat die Funktion des Befehls in der Praxis der Sprache. (Ähnlich sagt man »Du wirst das tun«, nicht als Prophezeiung, sondern als Befehl. Was macht es zu dem einen, was zu dem andern?)
22. Freges Ansicht, daß in einer Behauptung eine Annahme steckt, die dasjenige ist, was behauptet wird, basiert eigentlich auf der Möglichkeit, die es in unserer Sprache gibt, jeden Behauptungssatz in der Form zu schreiben »Es wird behauptet, daß das und das der Fall ist.« – Aber »Daß das und das der Fall ist«, ist eben in unsrer Sprache kein Satz – es ist noch kein Zug im Sprachspiel. Und schreibe ich statt »Es wird behauptet, daß ...« »Es wird behauptet: das und das ist der Fall«, dann sind hier die Worte »Es wird behauptet« eben überflüssig.
Wir könnten sehr gut auch jede Behauptung in der Form einer Frage mit nachgesetzter Bejahung schreiben; etwa: »Regnet es? Ja!« Würde das zeigen, daß in jeder Behauptung eine Frage steckt?
Man hat wohl das Recht, ein Behauptungszeichen zu verwenden im Gegensatz z.B. zu einem Fragezeichen; oder wenn man eine Behauptung unterscheiden will von einer Fiktion, oder einer Annahme. Irrig ist es nur, wenn man meint, daß die Behauptung nun aus zwei Akten besteht, dem Erwägen und dem Behaupten (Beilegen des Wahrheitswerts, oder dergl.) und daß wir diese Akte nach dem Zeichen des Satzes vollziehen, ungefähr wie wir nach Noten singen. Mit dem Singen nach Noten ist allerdings das laute, oder leise Lesen des geschriebenen Satzes zu vergleichen, aber nicht das ›Meinen‹ (Denken) des gelesenen Satzes.
Das Fregesche Behauptungszeichen betont den Satzanfang. Es hat also eine ähnliche Funktion wie der Schlusspunkt. Es unterscheidet die ganze Periode vom Satz in der Periode. Wenn ich Einen sagen höre »es regnet«, aber nicht weiß, ob ich den Anfang und den Schluß der Periode gehört habe, so ist dieser Satz für mich noch kein Mittel der Verständigung.
###
Denken wir uns ein Bild, einen Boxer in bestimmter Kampfstellung darstellend. Dieses Bild kann nun dazu gebraucht werden, um jemand mitzuteilen, wie er stehen, sich halten soll; oder, wie er sich nicht halten soll; oder, wie ein bestimmter Mann dort und dort gestanden hat; oder etc. etc. Man könnte dieses Bild (chemisch gesprochen) ein Satzradikal nennen. Ähnlich dachte sich wohl Frege die »Annahme«.
###
23. Wieviele Arten der Sätze gibt es aber? Etwa Behauptung, Frage und Befehl? – Es gibt unzählige solcher Arten: unzählige verschiedene Arten der Verwendung alles dessen, was wir »Zeichen«, »Worte«, »Sätze«, nennen. Und diese Mannigfaltigkeit ist nichts Festes, ein für allemal Gegebenes; sondern neue Typen der Sprache, neue Sprachspiele, wie wir sagen können, entstehen und andre veralten und werden vergessen. (Ein ungefähres Bild davon können uns die Wandlungen der Mathematik geben.)
Das Wort »Sprachspiel« soll hier hervorheben, daß das Sprechen der Sprache ein Teil ist einer Tätigkeit, oder einer Lebensform.
Führe dir die Mannigfaltigkeit der Sprachspiele an diesen Beispielen, und anderen, vor Augen:
Befehlen, und nach Befehlen handeln –
Beschreiben eines Gegenstands nach dem Ansehen, oder nach Messungen –
Herstellen eines Gegenstands nach einer Beschreibung (Zeichnung) –
Berichten eines Hergangs –
Über den Hergang Vermutungen anstellen –
Eine Hypothese aufstellen und prüfen –
Darstellen der Ergebnisse eines Experiments durch Tabellen und Diagramme –
Eine Geschichte erfinden; und lesen –
Theater spielen –
Reigen singen –
Rätsel raten –
Einen Witz machen; erzählen –
Ein angewandtes Rechenexempel lösen –
Aus einer Sprache in die andere übersetzen –
Bitten, Danken, Fluchen, Grüßen, Beten.
– Es ist interessant, die Mannigfaltigkeit der Werkzeuge der Sprache und ihrer Verwendungsweisen, die Mannigfaltigkeit der Wort- und Satzarten, mit dem zu vergleichen, was Logiker über den Bau der Sprache gesagt haben. (Und auch der Verfasser der Logisch-Philosophischen Abhandlung.)
24. Wem die Mannigfaltigkeit der Sprachspiele nicht vor Augen ist, der wird etwa zu den Fragen geneigt sein, wie dieser: »Was ist eine Frage?« – Ist es die Feststellung, daß ich das und das nicht weiß, oder die Feststellung, daß ich wünsche, der Andre möchte mir sagen....? Oder ist es die Beschreibung meines seelischen Zustandes der Ungewißheit? – Und ist der Ruf »Hilfe!« so eine Beschreibung?
Denke daran, wieviel Verschiedenartiges »Beschreibung« genannt wird: Beschreibung der Lage eines Körpers durch seine Koordinaten; Beschreibung eines Gesichtsausdrucks; Beschreibung einer Tastempfindung; einer Stimmung.
Man kann freilich statt der gewöhnlichen Form der Frage die der Feststellung, oder Beschreibung setzen: »Ich will wissen, ob,...«, oder »Ich bin im Zweifel, ob,...« – aber damit hat man die verschiedenen Sprachspiele einander nicht näher gebracht.
Die Bedeutsamkeit solcher Umformungsmöglichkeiten, z.B. aller Behauptungssätze in Sätze, die mit der Klausel »Ich denke«, oder »Ich glaube« anfangen (also sozusagen in Beschreibungen meines Innenlebens) wird sich an anderer Stelle deutlicher zeigen. (Solipsismus.)
25. Man sagt manchmal: die Tiere sprechen nicht, weil ihnen die geistigen Fähigkeiten fehlen. Und das heißt: »sie denken nicht, darum sprechen sie nicht«. Aber: sie sprechen eben nicht. Oder besser: sie verwenden die Sprache nicht – wenn wir von den primitivsten Sprachformen absehen. – Befehlen, fragen, erzählen, plauschen gehören zu unserer Naturgeschichte so wie gehen, essen, trinken, spielen.
26. Man meint, das Lernen der Sprache bestehe darin, daß man Gegenstände benennt. Und zwar: Menschen, Formen, Farben, Schmerzen, Stimmungen, Zahlen etc. Wie gesagt – das Benennen ist etwas Ähnliches, wie, einem Ding ein Namentäfelchen anheften. Man kann das eine Vorbereitung zum Gebrauch eines Wortes nennen. Aber worauf ist es eine Vorbereitung?
27. »Wir benennen die Dinge und können nun über sie reden. Uns in der Rede auf sie beziehen.« – Als ob mit dem Akt des Benennens schon das, was wir weiter tun, gegeben wäre. Als ob es nur Eines gäbe, was heißt: »von Dingen reden«. Während wir doch das Verschiedenartigste mit unsern Sätzen tun. Denken wir allein an die Ausrufe. Mit ihren ganz verschiedenen Funktionen.
Wasser!
Fort!
Au!
Hilfe!
Schön!
Nicht!
Bist du nun noch geneigt, diese Wörter »Benennungen von Gegenständen« zu nennen?
In den Sprachen (2) und (8) gab es ein Fragen nach der Benennung nicht. Dies und sein Korrelat, die hinweisende Erklärung, ist, wie wir sagen könnten, ein eigenes Sprachspiel. Das heißt eigentlich: wir werden erzogen, abgerichtet dazu, zu fragen: »Wie heißt das?« – worauf dann das Benennen erfolgt. Und es gibt auch ein Sprachspiel: Für etwas einen Namen erfinden. Also, zu sagen: »Das heißt....«, und nun den neuen Namen zu verwenden. (So benennen Kinder z.B. ihre Puppen und reden dann von ihnen, und zu ihnen. Dabei bedenke gleich, wie eigenartig der Gebrauch des Personennamens ist, mit welchem wir den Benannten rufen!)
28. Man kann nun einen Personennamen, ein Farbwort, einen Stoffnamen, ein Zahlwort, den Namen einer Himmelsrichtung, etc. hinweisend definieren. Die Definition der Zahl Zwei »Das heißt ›zwei‹« – wobei man auf zwei Nüsse zeigt – ist vollkommen exakt. – Aber wie kann man denn die Zwei so definieren? Der, dem man die Definition gibt, weiß ja dann nicht, was man mit »zwei« benennen will; er wird annehmen, daß du diese Gruppe von Nüssen »zwei« nennst! –– Er kann dies annehmen; vielleicht nimmt er es aber nicht an. Er könnte ja auch, umgekehrt, wenn ich dieser Gruppe von Nüssen einen Namen beilegen will, ihn als Zahlnamen mißverstehen. Und ebensogut, wenn ich einen Personennamen hinweisend erkläre, diesen als Farbnamen, als Bezeichnung der Rasse, ja als Namen einer Himmelsrichtung auffassen. Das heißt, die hinweisende Definition kann in jedem Fall so und anders gedeutet werden.
###
Könnte man zur Erklärung des Wortes »rot« auf etwas weisen, was nicht rot ist? Das wäre ähnlich, wie wenn man Einem, der der deutschen Sprache nicht mächtig ist, das Wort »bescheiden« erklären sollte, und man zeigte zur Erklärung auf einen arroganten Menschen und sagte »Dieser ist nicht bescheiden«. Es ist kein Argument gegen eine solche Erklärungsweise, daß sie vieldeutig ist. Jede Erklärung kann mißverstanden werden.
Wohl aber könnte man fragen: Sollen wir das noch eine »Erklärung« nennen? – Denn sie spielt im Kalkül natürlich eine andere Rolle als das, was wir gewöhnlich »hinweisende Erklärung« des Wortes »rot« nennen; auch wenn sie dieselben praktischen Folgen, dieselbe Wirkung auf den Lernenden hätte.
###
29. Vielleicht sagt man: die Zwei kann nur so hinweisend definiert werden: »Diese Zahl heißt ›zwei‹«. Denn das Wort »Zahl« zeigt hier an, an welchen Platz der Sprache, der Grammatik, wir das Wort setzen. Das heißt aber, es muß das Wort »Zahl« erklärt sein, ehe jene hinweisende Definition verstanden werden kann. – Das Wort »Zahl« in der Definition zeigt allerdings diesen Platz an; den Posten, an den wir das Wort stellen. Und wir können so Mißverständnissen vorbeugen, indem wir sagen: »Diese Farbe heißt so und so«, »Diese Länge heißt so und so«, usw. Das heißt: Mißverständnisse werden manchmal so vermieden. Aber läßt sich denn das Wort »Farbe«, oder »Länge« nur so auffassen? – Nun, wir müssen sie eben erklären. – Also erklären durch andere Wörter! Und wie ist es mit der letzten Erklärung in dieser Kette? (Sag nicht »Es gibt keine ›letzte‹ Erklärung«. Das ist gerade so, als wolltest du sagen: »Es gibt kein letztes Haus in dieser Straße; man kann immer noch eines dazubauen.«)
Ob das Wort »Zahl« in der hinweisenden Definition der Zwei nötig ist, das hängt davon ab, ob er sie ohne dieses Wort anders auffaßt, als ich es wünsche. Und das wird wohl von den Umständen abhängen, unter welchen sie gegeben wird, und von dem Menschen, dem ich sie gebe.
Und wie er die Erklärung ›auffaßt‹, zeigt sich darin, wie er von dem erklärten Wort Gebrauch macht.
30. Man könnte also sagen: Die hinweisende Definition erklärt den Gebrauch – die Bedeutung – des Wortes, wenn es schon klar ist, welche Rolle das Wort in der Sprache überhaupt spielen soll. Wenn ich also weiß, daß Einer mir ein Farbwort erklären will, so wird mir die hinweisende Erklärung »Das heißt ›Sepia‹« zum Verständnis des Wortes verhelfen. – Und dies kann man sagen, wenn man nicht vergißt, daß sich nun allerlei Fragen an das Wort »wissen«, oder »klar sein« anknüpfen.
Man muß schon etwas wissen (oder können), um nach der Benennung fragen zu können. Aber was muß man wissen?
31. Wenn man jemandem die Königsfigur im Schachspiel zeigt und sagt »Das ist der Schachkönig«, so erklärt man ihm dadurch nicht den Gebrauch dieser Figur, – es sei denn, daß er die Regeln des Spiels schon kennt, bis auf diese letzte Bestimmung: die Form einer Königsfigur. Man kann sich denken, er habe die Regeln des Spiels gelernt, ohne daß ihm je eine wirkliche Spielfigur gezeigt wurde. Die Form der Spielfigur entspricht hier dem Klang, oder der Gestalt eines Wortes.
Man kann sich aber auch denken, Einer habe das Spiel gelernt, ohne je Regeln zu lernen, oder zu formulieren. Er hat etwa zuerst durch Zusehen ganz einfache Brettspiele gelernt und ist zu immer komplizierteren fortgeschritten. Auch diesem könnte man die Erklärung geben: »Das ist der König« – wenn man ihm z.B. Schachfiguren von einer ihm ungewohnten Form zeigt. Auch diese Erklärung lehrt ihn den Gebrauch der Figur nur darum, weil, wie wir sagen könnten, der Platz schon vorbereitet war, an den sie gestellt wurde. Oder auch: Wir werden nur dann sagen, sie lehre ihn den Gebrauch, wenn der Platz schon vorbereitet ist. Und er ist es hier nicht dadurch, daß der, dem wir die Erklärung geben, schon Regeln weiß, sondern dadurch, daß er in anderm Sinne schon ein Spiel beherrscht.
Betrachte noch diesen Fall: Ich erkläre jemandem das Schachspiel; und fange damit an, indem ich auf eine Figur zeige und sage: »Das ist der König. Er kann so und so ziehen, etc. etc.«. – In diesem Fall werden wir sagen: die Worte »Das ist der König« (oder »Das heißt ›König‹«) sind nur dann eine Worterklärung, wenn der Lernende schon ›weiß, was eine Spielfigur ist‹. Wenn er also etwa schon andere Spiele gespielt hat, oder dem Spielen Anderer ›mit Verständnis‹ zugesehen hat – und dergleichen. Auch nur dann wird er beim Lernen des Spiels relevant fragen können: »Wie heißt das?« – nämlich, diese Spielfigur.
Wir können sagen: Nach der Benennung fragt nur der sinnvoll, der schon etwas mit ihr anzufangen weiß.
Wir können uns ja auch denken, daß der Gefragte antwortet: »Bestimm die Benennung selber« – und nun müßte, der gefragt hat, für alles selber aufkommen.
32. Wer in ein fremdes Land kommt, wird manchmal die Sprache der Einheimischen durch hinweisende Erklärungen lernen, die sie ihm geben; und er wird die Deutung dieser Erklärungen oft raten müssen und manchmal richtig, manchmal falsch raten.
Und nun können wir, glaube ich, sagen: Augustinus beschreibe das Lernen der menschlichen Sprache so, als käme das Kind in ein fremdes Land und verstehe die Sprache des Landes nicht; das heißt: so als habe es bereits eine Sprache, nur nicht diese. Oder auch: als könne das Kind schon denken, nur noch nicht sprechen. Und »denken« hieße hier etwas, wie: zu sich selber reden.
33. Wie aber, wenn man einwendete: »Es ist nicht wahr, daß Einer schon ein Sprachspiel beherrschen muß, um eine hinweisende Definition zu verstehen, sondern er muß nur – selbstverständlich – wissen (oder erraten) worauf der Erklärende zeigt! Ob also z.B. auf die Form des Gegenstandes, oder auf seine Farbe, oder auf die Anzahl, etc. etc.« –– Und worin besteht es denn – ›auf die Form zeigen‹, ›auf die Farbe zeigen‹? Zeig auf ein Stück Papier! – Und nun zeig auf seine Form, – nun auf seine Farbe, – nun auf seine Anzahl (das klingt seltsam!) – Nun, wie hast du es gemacht? – Du wirst sagen, du habest jedesmal etwas anderes beim Zeigen ›gemeint‹. Und wenn ich frage, wie das vor sich geht, wirst du sagen, du habest deine Aufmerksamkeit auf die Farbe, Form etc. konzentriert. Nun aber frage ich noch einmal, wie das vor sich geht.
Denke, jemand zeigt auf eine Vase und sagt: »Schau das herrliche Blau an! – auf die Form kommt es nicht an. – « Oder: »Schau die herrliche Form an! – die Farbe ist gleichgültig.« Es ist zweifellos, du wirst Verschiedenes tun, wenn du diesen beiden Aufforderungen nachkommst. Aber tust du immer das Gleiche, wenn du deine Aufmerksamkeit auf die Farbe richtest? Stell dir doch verschiedene Fälle vor! Ich will einige andeuten:
»Ist dieses Blau das gleiche, wie das dort? Siehst du einen Unterschied?« –
Du mischst die Farben und sagst: »Dieses Blau des Himmels ist schwer zu treffen.«
»Es wird schön, man sieht schon wieder blauen Himmel!«
»Schau, wie verschieden diese beiden Blau wirken!«
»Siehst du dort das blaue Buch? Bring es her.«
»Dieses blaue Lichtsignal bedeutet....«
»Wie heißt nur dieses Blau? – ist es ›Indigo‹?«
Die Aufmerksamkeit auf die Farbe richten, das tut man manchmal, indem man sich die Umrisse der Form mit der Hand weghält; oder den Blick nicht auf die Kontur des Dinges richtet; oder auf den Gegenstand starrt und sich zu erinnern trachtet, wo man diese Farbe schon gesehen hat.
Man richtet seine Aufmerksamkeit auf die Form, manchmal, indem man sie nachzeichnet, manchmal, indem man blinzelt, um die Farbe nicht deutlich zu sehen, etc. etc. Ich will sagen: dies und Ähnliches geschieht, während man ›die Aufmerksamkeit auf das und das richtetet‹. Aber das ist es nicht allein, was uns sagen läßt, Einer richte seine Aufmerksamkeit auf die Form, die Farbe, etc. Wie ein Schachzug nicht allein darin besteht, daß ein Stein so und so auf dem Brett verschoben wird, – aber auch nicht in den Gedanken und Gefühlen des Ziehenden, die den Zug begleiten; sondern in den Umständen, die wir nennen: »eine Schachpartie spielen«, »ein Schachproblem lösen«, und dergl.
34. Aber nimm an, Einer sagte: »Ich tue immer das Gleiche, wenn ich meine Aufmerksamkeit auf die Form richte: ich folge der Kontur mit den Augen und fühle dabei...«. Und nimm an, dieser gibt einem Andern die hinweisende Erklärung »Das heißt ›Kreis‹«, indem er, mit all diesen Erlebnissen, auf einen kreisförmigen Gegenstand zeigt –– kann der Andre die Erklärung nicht dennoch anders deuten, auch wenn er sieht, daß der Erklärende der Form mit den Augen folgt, und auch wenn er fühlt, was der Erklärende fühlt? Das heißt: diese ›Deutung‹ kann auch darin bestehen, wie er nun von dem erklärten Wort Gebrauch macht, z.B., worauf er zeigt, wenn er den Befehl erhält »Zeige auf einen Kreis!«. – Denn weder der Ausdruck »die Erklärung so und so meinen«, noch der, »die Erklärung so und so deuten«, bezeichnen einen Vorgang, der das Geben und Hören der Erklärung begleitet.
35. Es gibt freilich, was man »charakteristische Erlebnisse«, für das Zeigen auf die Form etwa, nennen kann. Zum Beispiel, das Nachfahren der Kontur mit dem Finger, oder mit dem Blick, beim Zeigen. – Aber so wenig, wie dies in allen Fällen geschieht, in denen ich ›die Form meine‹, so wenig geschieht irgend ein anderer charakteristischer Vorgang in allen diesen Fällen. – Aber auch, wenn ein solcher sich in allen wiederholte, so käme es doch auf die Umstände an – d.h., auf das, was vor und nach dem Zeigen geschieht – ob wir sagen würden »Er hat auf die Form und nicht auf die Farbe gezeigt«.
Denn es werden die Worte »auf die Form zeigen«, »die Form meinen« etc. nicht so gebraucht, wie die: »auf dies Buch zeigen« (nicht auf jenes), »auf den Stuhl zeigen, nicht auf den Tisch«, etc. – Denn denk nur, wie anders wir den Gebrauch der Worte lernen: »auf dieses Ding zeigen«, »auf jenes Ding zeigen«, und anderseits: »auf die Farbe, nicht auf die Form, zeigen«, »die Farbe meinen«, etc. etc.
Wie gesagt, in gewissen Fällen, besonders beim Zeigen ›auf die Form‹, oder ›auf die Anzahl‹ gibt es charakteristische Erlebnisse und Arten des Zeigens – ›charakteristisch‹, weil sie sich oft (nicht immer) wiederholen, wo Form, oder Anzahl ›gemeint‹ werden. Aber kennst du auch ein charakteristisches Erlebnis für das Zeigen auf die Spielfigur, als Spielfigur? Und doch kann man sagen: »Ich meine, diese Spielfigur heißt ›König‹, nicht dieses bestimmte Stück Holz, worauf ich zeige«. (Wiedererkennen, wünschen, sich erinnern, etc.)
###
Wie geht es vor sich: die Worte »Das ist blau« einmal als Aussage über den Gegenstand, auf den man zeigt – einmal als Erklärung des Wortes »blau« meinen? Im zweiten Fall meint man also eigentlich »Das heißt ›blau‹« – Kann man also das Wort »ist« einmal als »heißt« meinen, und das Wort »blau« als »›blau‹«? und ein andermal das »ist« wirklich als »ist«?
Es kann auch geschehen, daß jemand aus dem, was als Mitteilung gemeint war, eine Worterklärung zieht. [Hier liegt ein folgenschwerer Aberglaube verborgen.]
Kann ich mit dem Wort »bububu« meinen »Wenn es nicht regnet, werde ich spazieren gehen«? – Nur in einer Sprache kann ich etwas mit etwas meinen. Das zeigt klar, daß die Grammatik von »meinen« nicht ähnlich der ist des Ausdrucks »sich etwas vorstellen« und dergl.
###
36. Und wir tun hier, was wir in tausend ähnlichen Fällen tun: Weil wir nicht eine körperliche Handlung angeben können, die wir das Zeigen auf die Form (im Gegensatz z.B. zur Farbe) nennen, so sagen wir, es entspreche diesen Worten eine geistige Tätigkeit.
Wo unsere Sprache uns einen Körper vermuten läßt, und kein Körper ist, dort, möchten wir sagen, sei ein Geist.
37. Was ist die Beziehung zwischen Namen und Benanntem? – Nun, was ist sie? Schau auf das Sprachspiel (2), oder ein anderes! dort ist zu sehen, worin diese Beziehung etwa besteht. Diese Beziehung kann, unter vielem andern, auch darin bestehen, daß das Hören des Namens uns das Bild des Benannten vor die Seele ruft, und sie besteht unter anderem auch darin, daß der Name auf das Benannte geschrieben ist, oder daß er beim Zeigen auf das Benannte ausgesprochen wird.
38. Was benennt aber z.B. das Wort »dieses« im Sprachspiel (8), oder das Wort »das« in der hinweisenden Erklärung »Das heißt....«? – Wenn man keine Verwirrung anrichten will, so ist es am besten, man sagt gar nicht, daß diese Wörter etwas benennen. – Und merkwürdigerweise wurde von dem Worte »dieses« einmal gesagt, es sei der eigentliche Name. Alles, was wir sonst »Name« nennen, sei dies also nur in einem ungenauen, angenäherten Sinn.
Diese seltsame Auffassung rührt von einer Tendenz her, die Logik unserer Sprache zu sublimieren – wie man es nennen könnte. Die eigentliche Antwort darauf ist: »Name« nennen wir sehr Verschiedenes; das Wort »Name« charakterisiert viele verschiedene, miteinander auf viele verschiedene Weisen verwandte, Arten des Gebrauchs eines Worts; – aber unter diesen Arten des Gebrauchs ist nicht die des Wortes »dieses«.
Es ist wohl wahr, daß wir oft, z.B. in der hinweisenden Definition, auf das Benannte zeigen und dabei den Namen aussprechen. Und ebenso sprechen wir, z.B. in der hinweisenden Definition, das Wort »dieses« aus, indem wir auf ein Ding zeigen. Und das Wort »dieses« und ein Name stehen auch oft an der gleichen Stelle im Satzzusammenhang. Aber charakteristisch für den Namen ist es gerade, daß er durch das hinweisende »Das ist N« (oder »Das heißt ›N‹«) erklärt wird. Erklären wir aber auch: »Das heißt ›dieses‹«, oder »Dieses heißt ›dieses‹«?
Dies hängt mit der Auffassung des Benennens als eines, sozusagen, okkulten Vorgangs zusammen. Das Benennen erscheint als eine seltsame Verbindung eines Wortes mit einem Gegenstand. – Und so eine seltsame Verbindung hat wirklich statt, wenn nämlich der Philosoph, um herauszubringen, was die Beziehung zwischen Namen und Benanntem ist, auf einen Gegenstand vor sich starrt und dabei unzählige Male einen Namen wiederholt, oder auch das Wort »dieses«. Denn die philosophischen Probleme entstehen, wenn die Sprache feiert. Und da können wir uns allerdings einbilden, das Benennen sei irgend ein merkwürdiger seelischer Akt, quasi eine Taufe eines Gegenstandes. Und wir können so auch das Wort »dieses« gleichsam zu dem Gegenstand sagen, ihn damit ansprechen – ein seltsamer Gebrauch dieses Wortes, der wohl nur beim Philosophieren vorkommt.
39. Aber warum kommt man auf die Idee, gerade dieses Wort zum Namen machen zu wollen, wo es offenbar kein Name ist? – Gerade darum. Denn man ist versucht, gegen das, was gewöhnlich »Name« heißt, einen Einwand zu machen; und den kann man so ausdrücken: daß der Name eigentlich Einfaches bezeichnen soll. Und man könnte dies etwa so begründen: Ein Eigenname im gewöhnlichen Sinn ist etwa das Wort »Nothung«. Das Schwert Nothung besteht aus Teilen in einer bestimmten Zusammensetzung. Sind sie anders zusammengesetzt, so existiert Nothung nicht. Nun hat aber offenbar der Satz »Nothung hat eine scharfe Schneide« Sinn, ob Nothung noch ganz ist, oder schon zerschlagen. Ist aber »Nothung« der Name eines Gegenstandes, so gibt es diesen Gegenstand nicht mehr, wenn Nothung zerschlagen ist; und da dem Namen dann kein Gegenstand entspräche, so hätte er keine Bedeutung. Dann aber stünde in dem Satz »Nothung hat eine scharfe Schneide« ein Wort, das keine Bedeutung hat, und daher wäre der Satz Unsinn. Nun hat er aber Sinn; also muß den Wörtern, aus denen er besteht, immer etwas entsprechen. Also muß das Wort »Nothung« bei der Analyse des Sinnes verschwinden und statt seiner müssen Wörter eintreten, die Einfaches benennen. Diese Wörter werden wir billigerweise die eigentlichen Namen nennen.
40. Laß uns zuerst über den Punkt dieses Gedankengangs reden: daß das Wort keine Bedeutung hat, wenn ihm nichts entspricht. – Es ist wichtig, festzustellen, daß das Wort »Bedeutung« sprachwidrig gebraucht wird, wenn man damit das Ding bezeichnet, das dem Wort ›entspricht‹. Dies heißt, die Bedeutung eines Namens verwechseln mit dem Träger des Namens. Wenn Herr N. N. stirbt, so sagt man, es sterbe der Träger des Namens, nicht, es sterbe die Bedeutung des Namens. Und es wäre unsinnig, so zu reden, denn hörte der Name auf, Bedeutung zu haben, so hätte es keinen Sinn, zu sagen »Herr N. N. ist gestorben«.
41. Im § 15 haben wir in die Sprache (8) Eigennamen eingeführt. Nimm nun an, das Werkzeug mit dem Namen »N« sei zerbrochen. A weiß es nicht und gibt dem B das Zeichen »N«. Hat dieses Zeichen nun Bedeutung, oder hat es keine? – Was soll B tun, wenn er dieses Zeichen erhält? – Wir haben darüber nichts vereinbart. Man könnte fragen: was wird er tun? Nun, er wird vielleicht ratlos dastehen, oder A die Stücke zeigen. Man könnte hier sagen: »N« sei bedeutungslos geworden; und dieser Ausdruck würde besagen, daß für das Zeichen »N« in unserm Sprachspiel nun keine Verwendung mehr ist (es sei denn, wir gäben ihm eine neue). »N« könnte auch dadurch bedeutungslos werden, daß man, aus welchem Grund immer, dem Werkzeug eine andere Bezeichnung gibt und das Zeichen »N« im Sprachspiel nicht weiter verwendet. – Wir können uns aber auch eine Abmachung denken, nach der B, wenn ein Werkzeug zerbrochen ist und A das Zeichen dieses Werkzeugs gibt, als Antwort darauf den Kopf zu schütteln hat. – Damit, könnte man sagen, ist der Befehl »N«, auch wenn dieses Werkzeug nicht mehr existiert, in das Sprachspiel aufgenommen worden, und das Zeichen »N« habe Bedeutung, auch wenn sein Träger zu existieren aufhört.
42. Aber haben etwa auch Namen in jenem Spiel Bedeutung, die nie für ein Werkzeug verwendet worden sind? –– Nehmen wir also an, »X« sei so ein Zeichen, und A gäbe dieses Zeichen dem B – nun, es könnten auch solche Zeichen in das Sprachspiel aufgenommen werden, und B hätte etwa auch sie mit einem Kopfschütteln zu beantworten. (Man könnte sich dies als eine Art Belustigung der Beiden denken.)
43. Man kann für eine große Klasse von Fällen der Benützung des Wortes »Bedeutung« – wenn auch nicht für alle Fälle seiner Benützung – dieses Wort so erklären: Die Bedeutung eines Wortes ist sein Gebrauch in der Sprache.
Und die Bedeutung eines Namens erklärt man manchmal dadurch, daß man auf seinen Träger zeigt.
44. Wir sagten: der Satz »Nothung hat eine scharfe Schneide« habe Sinn, auch wenn Nothung schon zerschlagen ist. Nun, das ist so, weil in diesem Sprachspiel ein Name auch in der Abwesenheit seines Trägers gebraucht wird. Aber wir können uns ein Sprachspiel mit Namen denken (d. h. mit Zeichen, die wir gewiß auch »Namen« nennen werden), in welchem diese nur in der Anwesenheit des Trägers gebraucht werden; also immer ersetzt werden können durch das hinweisende Fürwort mit der hinweisenden Gebärde.
45. Das hinweisende »dieses« kann nie trägerlos werden. Man könnte sagen: »Solange es ein Dieses gibt, solange hat das Wort ›dieses‹ auch Bedeutung, ob dieses nun einfach oder zusammengesetzt ist.« –– Aber das macht das Wort eben nicht zu einem Namen. Im Gegenteil; denn ein Name wird nicht mit der hinweisenden Geste verwendet, sondern nur durch sie erklärt.
46. Was hat es nun für eine Bewandtnis damit, daß Namen eigentlich das Einfache bezeichnen ? –
Sokrates (im Theätetus): »Täusche ich mich nämlich nicht, so habe ich von Etlichen gehört: für die Urelemente – um mich so auszudrücken – aus denen wir und alles übrige zusammengesetzt sind, gebe es keine Erklärung; denn alles, was an und für sich ist, könne man nur mit Namen bezeichnen; eine andere Bestimmung sei nicht möglich, weder die, es sei, noch die, es sei nicht .... Was aber an und für sich ist, müsse man .... ohne alle anderen Bestimmungen benennen. Somit aber sei es unmöglich, von irgend einem Urelement erklärungsweise zu reden; denn für dieses gebe es nichts als die bloße Benennung; es habe ja nur seinen Namen. Wie aber das, was aus diesen Urelementen sich zusammensetzt, selbst ein verflochtenes Gebilde sei, so seien auch seine Benennungen in dieser Verflechtung zur erklärenden Rede geworden; denn deren Wesen sei die Verflechtung von Namen.«[1]
Diese Urelemente waren auch Russell’s ›individuals‹, und auch meine ›Gegenstände‹ (Log. Phil. Abh.).
47. Aber welches sind die einfachen Bestandteile, aus denen sich die Realität zusammensetzt? – Was sind die einfachen Bestandteile eines Sessels? – Die Stücke Holz, aus denen er zusammengefügt ist? Oder die Moleküle, oder die Atome? – »Einfach« heißt: nicht zusammengesetzt. Und da kommt es darauf an: in welchem Sinne ›zusammengesetzt‹? Es hat gar keinen Sinn von den ›einfachen Bestandteilen des Sessels schlechtweg‹ zu reden.
Oder: Besteht mein Gesichtsbild dieses Baumes, dieses Sessels, aus Teilen? und welches sind seine einfachen Bestandteile? Mehrfarbigkeit ist eine Art der Zusammengesetztheit; eine andere ist, z.B., die einer gebrochenen Kontur aus geraden Stücken. Und ein Kurvenstück kann man zusammengesetzt nennen aus einem aufsteigenden und einem absteigenden Ast.
Wenn ich jemandem ohne weitere Erklärung sage »Was ich jetzt vor mir sehe, ist zusammengesetzt«, so wird er mit Recht fragen: »Was meinst du mit ›zusammengesetzt‹? Das kann ja alles Mögliche heißen!« – Die Frage »Ist, was du siehst, zusammengesetzt?« hat wohl Sinn, wenn bereits feststeht, um welche Art des Zusammengesetztseins – d.h., um welchen besonderen Gebrauch dieses Wortes – es sich handeln soll. Wäre festgelegt worden, das Gesichtsbild eines Baumes solle »zusammengesetzt« heißen, wenn man nicht nur einen Stamm, sondern auch Aste sieht, so hätte die Frage »Ist das Gesichtsbild dieses Baumes einfach oder zusammengesetzt?« und die Frage »Welches sind seine einfachen Bestandteile?« einen klaren Sinn – eine klare Verwendung. Und auf die zweite Frage ist die Antwort natürlich nicht »Die Äste« (dies wäre eine Antwort auf die grammatische Frage: »Was nennt man hier die ›einfachen Bestandteile‹?«) sondern etwa eine Beschreibung der einzelnen Äste.
Aber ist z.B. nicht ein Schachbrett offenbar und schlechtweg zusammengesetzt? – Du denkst wohl an die Zusammensetzung aus 32 weißen und 32 schwarzen Quadraten. Aber könnten wir z.B. nicht auch sagen, es sei aus den Farben Weiß, Schwarz und dem Schema des Quadratnetzes zusammengesetzt? Und wenn es hier ganz verschiedene Betrachtungsweisen gibt, willst du dann noch sagen, das Schachbrett sei ›zusammengesetzt‹ schlechtweg? – Außerhalb eines bestimmten Spiels zu fragen »Ist dieser Gegenstand zusammengesetzt?«, das ist ähnlich dem, was einmal ein Junge tat, der angeben sollte, ob die Zeitwörter in gewissen Satzbeispielen in der aktiven, oder in der passiven Form gebraucht seien, und der sich nun darüber den Kopf zerbrach, ob z.B. das Zeitwort »schlafen« etwas Aktives oder etwas Passives bedeute.
Das Wort »zusammengesetzt« (und also das Wort »einfach«) wird von uns in einer Unzahl verschiedener, in verschiedenen Weisen miteinander verwandten, Arten benützt. (Ist die Farbe eines Schachfeldes einfach, oder besteht sie aus reinem Weiß und reinem Gelb? Und ist das Weiß einfach, oder besteht es aus den Farben des Regenbogens? – Ist diese Strecke von 2 cm einfach, oder besteht sie aus zwei Teilstrecken von je 1 cm? Aber warum nicht aus einem Stück von 3 cm Länge und einem, in negativem Sinn angesetzten, Stück von 1 cm?)
Auf die philosophische Frage: »Ist das Gesichtsbild dieses Baumes zusammengesetzt, und welches sind seine Bestandteile?« ist die richtige Antwort: »Das kommt drauf an, was du unter ›zusammengesetzt‹ verstehst.« (Und das ist natürlich keine Beantwortung, sondern eine Zurückweisung der Frage.)
[1]###Preisendanz’s Übersetzung.###
48. Laß uns die Methode des § 2 auf die Darstellung im Theätetus anwenden. Betrachten wir ein Sprachspiel, wofür diese Darstellung wirklich gilt. Die Sprache diene dazu, Kombinationen farbiger Quadrate auf einer Fläche darzustellen. Die Quadrate bilden einen schachbrettförmigen Komplex. Es gibt rote, grüne, weiße und schwarze Quadrate. Die Wörter der Sprache seien (entsprechend): »R«, »G«, »W«, »S«, und ein Satz ist eine Reihe dieser Wörter. Sie beschreiben eine Zusammenstellung von Quadraten in der Reihenfolge

Der Satz »RRSGGGRWW« beschreibt also z.B. eine Zusammensetzung dieser Art:

Hier ist der Satz ein Komplex von Namen, dem ein Komplex von Elementen entspricht. Die Urelemente sind die farbigen Quadrate. »Aber sind diese einfach?« – Ich wüßte nicht, was ich in diesem Sprachspiel natürlicher das »Einfache« nennen sollte. Unter anderen Umständen aber würde ich ein einfarbiges Quadrat »zusammengesetzt« nennen, etwa aus zwei Rechtecken, oder aus den Elementen Farbe und Form. Aber der Begriff der Zusammensetzung könnte auch so gedehnt werden, daß die kleinere Fläche ›zusammengesetzt‹ genannt wird aus einer größeren und einer von ihr subtrahierten. Vergleiche ›Zusammensetzung‹ der Kräfte, ›Teilung‹ einer Strecke durch einen Punkt außerhalb; diese Ausdrücke zeigen, daß wir unter Umständen auch geneigt sind, das Kleinere als Resultat der Zusammensetzung von Größerem aufzufassen und das Größere als ein Resultat der Teilung des Kleineren.
Aber ich weiß nicht, ob ich nun sagen soll, die Figur, die unser Satz beschreibt, bestehe aus vier Elementen oder aus neun! Nun, besteht jener Satz aus vier Buchstaben oder aus neun? – Und welches sind seine Elemente: die Buchstabentypen, oder die Buchstaben? Ist es nicht gleichgültig, welches wir sagen? wenn wir nur im besonderen Fall Mißverständnisse vermeiden!
49. Was heißt es aber, daß wir diese Elemente nicht erklären (d.h. beschreiben) sondern nur benennen können? Das könnte etwa sagen, daß die Beschreibung eines Komplexes, wenn er, in einem Grenzfall, nur aus einem Quadrat besteht, einfach der Name des Farbquadrates ist.
Man könnte hier sagen – obwohl dies leicht zu allerlei philosophischem Aberglauben führt – ein Zeichen »R«, oder »S«, etc., könne einmal Wort und einmal Satz sein. Ob es aber ›Wort oder Satz ist‹, hängt von der Situation ab, in der es ausgesprochen oder geschrieben wird. Soll z. B. A dem B Komplexe von Farbquadraten beschreiben und gebraucht er hier das Wort »R« allein, so werden wir sagen können, das Wort sei eine Beschreibung – ein Satz. Memoriert er aber etwa die Wörter und ihre Bedeutungen, oder lehrt er einen Andern den Gebrauch der Wörter und spricht sie beim hinweisenden Lehren aus, so werden wir nicht sagen, sie seien hier Sätze. In dieser Situation ist das Wort »R« z.B. keine Beschreibung; man benennt damit ein Element –– aber darum wäre es hier seltsam zu sagen, das Element könne man nur benennen! Benennen und Beschreiben stehen ja nicht auf einer Ebene: Das Benennen ist eine Vorbereitung zur Beschreibung. Das Benennen ist noch gar kein Zug im Sprachspiel, – so wenig, wie das Aufstellen einer Schachfigur ein Zug im Schachspiel. Man kann sagen: Mit dem Benennen eines Dings ist noch nichts getan. Es hat auch keinen Namen, außer im Spiel. Das war es auch, was Frege damit meinte: ein Wort habe nur im Satzzusammenhang Bedeutung.
50. Was heißt es nun, von den Elementen zu sagen, daß wir ihnen weder Sein noch Nichtsein beilegen können? – Man könnte sagen: Wenn alles, was wir »Sein« oder »Nichtsein« nennen, im Bestehen und Nichtbestehen von Verbindungen zwischen den Elementen liegt, dann hat es keinen Sinn vom Sein (Nichtsein) eines Elements zu sprechen; sowie, wenn alles, was wir »zerstören« nennen, in der Trennung von Elementen liegt, es keinen Sinn hat, vom Zerstören eines Elements zu reden.
Aber man möchte sagen: Man kann dem Element nicht Sein beilegen, denn wäre es nicht, so könnte man es auch nicht einmal nennen und also gar nichts von ihm aussagen. – Betrachten wir doch einen analogen Fall! Man kann von einem Ding nicht aussagen, es sei 1 m lang, noch, es sei nicht 1 m lang, und das ist das Urmeter in Paris. – Damit haben wir aber diesem natürlich nicht irgend eine merkwürdige Eigenschaft zugeschrieben, sondern nur seine eigenartige Rolle im Spiel des Messens mit dem Metermaß gekennzeichnet. – Denken wir uns auf ähnliche Weise wie das Urmeter auch die Muster von Farben in Paris aufbewahrt. So erklären wir: »Sepia« heiße die Farbe des dort unter Luftabschluß aufbewahrten Ur-Sepia. Dann wird es keinen Sinn haben, von diesem Muster auszusagen, es habe diese Farbe, noch, es habe sie nicht.
Wir können das so ausdrücken: Dieses Muster ist ein Instrument der Sprache, mit der wir Farbaussagen machen. Es ist in diesem Spiel nicht Dargestelltes, sondern Mittel der Darstellung. – Und eben das gilt von einem Element im Sprachspiel (48), wenn wir, es benennend, das Wort »R« aussprechen: wir haben damit diesem Ding eine Rolle in unserm Sprachspiel gegeben; es ist nun Mittel der Darstellung. Und zu sagen »Wäre es nicht, so könnte es keinen Namen haben« sagt nun so viel, und so wenig, wie: gäbe es dieses Ding nicht, so könnten wir es in unserem Spiel nicht verwenden. – Was es, scheinbar, geben muß, gehört zur Sprache. Es ist in unserem Spiel ein Paradigma; etwas, womit verglichen wird. Und dies feststellen, kann heißen, eine wichtige Feststellung machen; aber es ist dennoch eine Feststellung unser Sprachspiel – unsere Darstellungsweise – betreffend.
51. In der Beschreibung des Sprachspiels (48) sagte ich, den Farben der Quadrate entsprächen die Wörter »R«, »S«, etc. Worin aber besteht diese Entsprechung, in wiefern kann man sagen, diesen Zeichen entsprächen gewisse Farben der Quadrate? Die Erklärung in (48) stellte ja nur einen Zusammenhang zwischen diesen Zeichen und gewissen Wörtern unserer Sprache her (den Farbnamen). – Nun, es war vorausgesetzt, daß der Gebrauch der Zeichen im Spiel anders, und zwar durch Hinweisen auf Paradigmen, gelehrt würde. Wohl; aber was heißt es nun, zu sagen, in der Praxis der Sprache entsprächen den Zeichen gewisse Elemente? – Liegt es darin, daß der, welcher die Komplexe von Farbquadraten beschreibt, hierbei immer »R« sagt, wo ein rotes Quadrat steht; »S«, wo ein schwarzes steht, etc.? Aber wie, wenn er sich bei der Beschreibung irrt und, fälschlich, »R« sagt, wo er ein schwarzes Quadrat sieht –– was ist hier das Kriterium dafür, daß dies ein Fehler war? – Oder besteht, daß »R« ein rotes Quadrat bezeichnet, darin, daß den Menschen, die die Sprache gebrauchen, immer ein rotes Quadrat im Geist vorschwebt, wenn sie das Zeichen »R« gebrauchen?
Um klarer zu sehen, müssen wir hier, wie in unzähligen ähnlichen Fällen, die Einzelheiten der Vorgänge ins Auge fassen; was vorgeht aus der Nähe betrachten.
52. Wenn ich dazu neige, anzunehmen, daß eine Maus durch Urzeugung aus grauen Fetzen und Staub entsteht, so wird es gut sein, diese Fetzen genau daraufhin zu untersuchen, wie eine Maus sich in ihnen verstecken konnte, wie sie dort hinkommen konnte, etc. Bin ich aber überzeugt, daß eine Maus aus diesen Dingen nicht entstehen kann, dann wird diese Untersuchung vielleicht überflüssig sein.
Was es aber ist, das sich in der Philosophie einer solchen Betrachtung der Einzelheiten entgegensetzt, müssen wir erst verstehen lernen.
53. Es gibt nun verschiedene Möglichkeiten für unser Sprachspiel (48), verschiedene Fälle, in denen wir sagen würden, ein Zeichen benenne in dem Spiel ein Quadrat von der und der Farbe. Wir würden dies z.B. sagen, wenn wir wüßten, daß den Menschen, die diese Sprache gebrauchen, der Gebrauch der Zeichen auf die und die Art beigebracht wurde. Oder, wenn es schriftlich, etwa in Form einer Tabelle, niedergelegt wäre, daß diesem Zeichen dieses Element entspricht, und wenn diese Tabelle beim Lehren der Sprache benützt und in gewissen Streitfällen zur Entscheidung herangezogen würde.
Wir können uns aber auch denken, daß eine solche Tabelle ein Werkzeug im Gebrauch der Sprache ist. Die Beschreibung eines Komplexes geht dann so vor sich: Der den Komplex beschreibt, führt eine Tabelle mit sich und sucht in ihr jedes Element des Komplexes auf und geht von ihm in der Tabelle zum Zeichen über (und es kann auch der, dem die Beschreibung gegeben wird, die Worte derselben durch eine Tabelle in die Anschauung von farbigen Quadraten übersetzen). Man könnte sagen, diese Tabelle übernehme hier die Rolle, die in anderen Fällen Gedächtnis und Assoziation spielen. (Wir werden den Befehl »Bring mir eine rote Blume!« für gewöhnlich nicht so ausführen, daß wir die Farbe Rot in einer Farbentabelle aufsuchen und dann eine Blume bringen von der Farbe, die wir in der Tabelle finden; aber wenn es sich darum handelt, einen bestimmten Ton von Rot zu wählen, oder zu mischen, dann geschieht es, daß wir uns eines Musters oder einer Tabelle bedienen.)
Nennen wir eine solche Tabelle den Ausdruck einer Regel des Sprachspiels, so kann man sagen, daß dem, was wir Regel eines Sprachspiels nennen, sehr verschiedene Rollen im Spiel zukommen können.
54. Denken wir doch daran, in was für Fällen wir sagen, ein Spiel werde nach einer bestimmten Regel gespielt!
Die Regel kann ein Behelf des Unterrichts im Spiel sein. Sie wird dem Lernenden mitgeteilt und ihre Anwendung eingeübt. – Oder sie ist ein Werkzeug des Spieles selbst. – Oder: Eine Regel findet weder im Unterricht noch im Spiel selbst Verwendung; noch ist sie in einem Regelverzeichnis niedergelegt. Man lernt das Spiel, indem man zusieht, wie Andere es spielen. Aber wir sagen, es werde nach den und den Regeln gespielt, weil ein Beobachter diese Regeln aus der Praxis des Spiels ablesen kann, – wie ein Naturgesetz, dem die Spielhandlungen folgen. –– Wie aber unterscheidet der Beobachter in diesem Fall zwischen einem Fehler der Spielenden und einer richtigen Spielhandlung? – Es gibt dafür Merkmale im Benehmen der Spieler. Denke an das charakteristische Benehmen dessen, der ein Versprechen korrigiert. Es wäre möglich, zu erkennen, daß Einer dies tut, auch wenn wir seine Sprache nicht verstehen.
55. »Was die Namen der Sprache bezeichnen, muß unzerstörbar sein: denn man muß den Zustand beschreiben können, in dem alles, was zerstörbar ist, zerstört ist. Und in dieser Beschreibung wird es Wörter geben; und was ihnen entspricht, darf dann nicht zerstört sein, denn sonst hätten die Wörter keine Bedeutung.« Ich darf mir nicht den Ast absägen, auf welchem ich sitze.
Man könnte nun freilich gleich einwenden, daß ja die Beschreibung selbst sich von der Zerstörung ausnehmen müsse. – Aber das, was den Wörtern der Beschreibung entspricht und also nicht zerstört sein darf, wenn sie wahr ist, ist, was den Wörtern ihre Bedeutung gibt, – ohne welches sie keine Bedeutung hätten. –– Aber dieser Mensch ist ja doch in einem Sinne das, was seinem Namen entspricht. Er aber ist zerstörbar; und sein Name verliert seine Bedeutung nicht, wenn der Träger zerstört wird. – Das, was dem Namen entspricht, und ohne den er keine Bedeutung hätte, ist, z.B., ein Paradigma, das im Sprachspiel in Verbindung mit dem Namen gebraucht wird.
56. Aber wie, wenn kein solches Muster zur Sprache gehört, wenn wir uns, z. B., die Farbe, die ein Wort bezeichnet, merken? –– »Und wenn wir sie uns merken, so tritt sie also vor unser geistiges Auge, wenn wir etwa das Wort aussprechen. Sie muß also an sich unzerstörbar sein, wenn die Möglichkeit bestehen soll, daß wir uns jederzeit an sie erinnern.« –– Aber was sehen wir denn als das Kriterium dafür an, daß wir uns richtig an sie erinnern? – Wenn wir mit einem Muster statt mit unserm Gedächtnis arbeiten, so sagen wir unter Umständen, das Muster habe seine Farbe verändert und beurteilen dies mit dem Gedächtnis. Aber können wir nicht unter Umständen auch von einem Nachdunkeln (z.B.) unseres Erinnerungsbildes reden? Sind wir dem Gedächtnis nicht ebenso ausgeliefert wie einem Muster? (Denn es könnte Einer sagen wollen: »Wenn wir kein Gedächtnis hätten, wären wir einem Muster ausgeliefert.«) – Oder etwa einer chemischen Reaktion. Denke, du solltest eine bestimmte Farbe »F« malen, und es ist die Farbe, welche man sieht, wenn sich die chemischen Substanzen X und Y miteinander verbinden. – Nimm an, die Farbe käme dir an einem Tag heller vor als an einem andern; würdest du da nicht unter Umständen sagen: »Ich muß mich irren, die Farbe ist gewiß die gleiche wie gestern«? Das zeigt, daß wir uns dessen, was das Gedächtnis sagt, nicht immer als des obersten, inappellabeln, Schiedsspruchs bedienen.
57. »Etwas Rotes kann zerstört werden, aber Rot kann nicht zerstört werden, und darum ist die Bedeutung des Wortes ›rot‹ von der Existenz eines roten Dinges unabhängig.« – Gewiß, es hat keinen Sinn, zu sagen, die Farbe Rot (color, nicht pigmentum) werde zerrissen, oder zerstampft. Aber sagen wir nicht, »Die Röte verschwindet«? Und klammre dich nicht daran, daß wir sie uns vors geistige Auge rufen können, auch wenn es nichts Rotes mehr gibt! Dies ist nicht anders, als wolltest du sagen, daß es dann immer noch eine chemische Reaktion gäbe, die eine rote Flamme erzeugt. – Denn wie, wenn du dich nicht mehr an die Farbe erinnern kannst? – Wenn wir vergessen, welche Farbe es ist, die diesen Namen hat, so verliert er seine Bedeutung für uns; d.h., wir können ein bestimmtes Sprachspiel nicht mehr mit ihm spielen. Und die Situation ist dann der zu vergleichen, daß das Paradigma, welches ein Mittel unserer Sprache war, verlorengegangen ist.
58. »Ich will ›Name‹ nur das nennen, was nicht in der Verbindung ›X existiert‹ stehen kann. – Und so kann man nicht sagen ›Rot existiert‹, weil, wenn es Rot nicht gäbe, von ihm überhaupt nicht geredet werden könnte.« – Richtiger: Wenn »X existiert« soviel besagen soll, wie: »X« habe Bedeutung, – dann ist es kein Satz, der von X handelt, sondern ein Satz über unsern Sprachgebrauch, nämlich den Gebrauch des Wortes »X«.
Es erscheint uns, als sagten wir damit etwas über die Natur von Rot: daß die Worte »Rot existiert« keinen Sinn ergeben. Es existiere eben ›an und für sich‹. Die gleiche Idee, – daß dies eine metaphysische Aussage über Rot ist, – drückt sich auch darin aus, daß wir etwa sagen, Rot sei zeitlos, und vielleicht noch stärker im Wort »unzerstörbar«.
Aber eigentlich wollen wir eben nur »Rot existiert« auffassen als Aussage: das Wort »Rot« hat Bedeutung. Oder vielleicht richtiger: »Rot existiert nicht« als » ›Rot‹ hat keine Bedeutung«. Nur wollen wir nicht sagen, daß jener Ausdruck das sagt, sondern daß er das sagen müßte, wenn er einen Sinn hätte. Daß er sich aber beim Versuch, das zu sagen, selbst widerspricht – da eben Rot ›an und für sich‹ sei. Während ein Widerspruch nur etwa darin liegt, daß der Satz aussieht, als rede er von der Farbe, während er etwas über den Gebrauch des Wortes »rot« sagen soll. – In Wirklichkeit aber sagen wir sehr wohl, eine bestimmte Farbe existiere; und das heißt soviel wie: es existiere etwas, was diese Farbe hat. Und der erste Ausdruck ist nicht weniger exakt als der zweite; besonders dort nicht, wo ›das, was die Farbe hat‹, kein physikalischer Gegenstand ist.
59. »Namen bezeichnen nur das, was Element der Wirklichkeit ist. Was sich nicht zerstören läßt; was in allem Wandel gleichbleibt.« – Aber was ist das? – Während wir den Satz sagten, schwebte es uns ja schon vor! Wir sprachen schon eine ganz bestimmte Vorstellung aus. Ein bestimmtes Bild, das wir verwenden wollen. Denn die Erfahrung zeigt uns diese Elemente ja nicht. Wir sehen Bestandteile von etwas Zusammengesetztem (eines Sessels z.B.). Wir sagen, die Lehne ist ein Teil des Sessels, aber selbst wieder zusammengesetzt aus verschiedenen Hölzern; während ein Fuß ein einfacher Bestandteil ist. Wir sehen auch ein Ganzes, was sich ändert (zerstört wird), während seine Bestandteile unverändert bleiben. Dies sind die Materialien, aus denen wir jenes Bild der Wirklichkeit anfertigen.
60. Wenn ich nun sage: »Mein Besen steht in der Ecke«, – ist dies eigentlich eine Aussage über den Besenstiel und die Bürste des Besens? Jedenfalls könnte man doch die Aussage ersetzen durch eine, die die Lage des Stiels und die Lage der Bürste angibt. Und diese Aussage ist doch nun wie eine weiter analysierte Form der ersten. – Warum aber nenne ich sie »weiter analysiert«? – Nun, wenn der Besen sich dort befindet, so heißt das doch, es müssen Stiel und Bürste dort sein und in bestimmter Lage zueinander; und dies war früher gleichsam im Sinn des Satzes verborgen, und im analysierten Satz ist es ausgesprochen. Also meint der, der sagt, der Besen stehe in der Ecke, eigentlich: der Stiel sei dort und die Bürste, und der Stiel stecke in der Bürste? – Wenn wir jemand fragten, ob er das meint, würde er wohl sagen, daß er gar nicht an den Besenstiel besonders, oder an die Bürste besonders, gedacht habe. Und das wäre die richtige Antwort, denn er wollte weder vom Besenstiel, noch von der Bürste besonders reden. Denke, du sagtest jemandem statt »Bring mir den Besen!« – »Bring mir den Besenstiel und die Bürste, die an ihm steckt!« – Ist die Antwort darauf nicht: »Willst du den Besen haben? Und warum drückst du das so sonderbar aus?« –– Wird er den weiter analysierten Satz also besser verstehen? – Dieser Satz, könnte man sagen, leistet dasselbe, wie der gewöhnliche, aber auf einem umständlicheren Wege. – Denk dir ein Sprachspiel, in dem jemandem Befehle gegeben werden, gewisse, aus mehreren Teilen zusammengesetzte, Dinge zu bringen, zu bewegen, oder dergleichen. Und zwei Arten es zu spielen: in der einen (a) haben die zusammengesetzten Dinge (Besen, Stühle, Tische, etc.) Namen, wie in (15); in anderen (b) erhalten nur die Teile Namen und das Ganze wird mit ihrer Hilfe beschrieben. – In wiefern ist denn ein Befehl des zweiten Spiels eine analysierte Form eines Befehls des ersten? Steckt denn jener in diesem und wird nun durch Analyse herausgeholt? – Ja, der Besen wird zerlegt, wenn man Stiel und Bürste trennt; aber besteht darum auch der Befehl, den Besen zu bringen, aus entsprechenden Teilen?
61. »Aber du wirst doch nicht leugnen, daß ein bestimmter Befehl in (a) das Gleiche sagt, wie einer in (b); und wie willst du denn den zweiten nennen, wenn nicht eine analysierte Form des ersten?« – Freilich, ich würde auch sagen, ein Befehl in (a) habe den gleichen Sinn, wie einer in (b); oder, wie ich es früher ausgedrückt habe: sie leisten dasselbe. Und das heißt: Wenn mir etwa ein Befehl in (a) gezeigt und die Frage gestellt würde »Welchem Befehl in (b) ist dieser gleichsinnig?«, oder auch »Welchen Befehlen in (b) widerspricht er?«, so werde ich die Frage so und so beantworten. Aber damit ist nicht gesagt, daß wir uns über die Verwendung des Ausdrucks »den gleichen Sinn haben«, oder »dasselbe leisten« im Allgemeinen verständigt haben. Man kann nämlich fragen: In welchem Fall sagen wir »Das sind nur zwei verschiedene Formen desselben Spiels«?
62. Denke etwa, der, dem die Befehle in (a) und (b) gegeben werden, habe in einer Tabelle, welche Namen und Bilder einander zuordnet, nachzusehen, ehe er das Verlangte bringt. Tut er nun dasselbe, wenn er einen Befehl in (a) und den entsprechenden in (b) ausführt? – Ja und nein. Du kannst sagen: »Der Witz der beiden Befehle ist der gleiche«. Ich würde hier dasselbe sagen. – Aber es ist nicht überall klar, was man den ›Witz‹ des Befehls nennen soll. (Ebenso kann man von gewissen Dingen sagen: ihr Zweck ist der und der. Das Wesentliche ist, daß das eine Lampe ist, zur Beleuchtung dient –– daß sie das Zimmer schmückt, einen leeren Raum füllt, etc., ist nicht wesentlich. Aber nicht immer sind wesentlich und unwesentlich klar getrennt.)
63. Der Ausdruck aber, ein Satz in (b) sei eine ›analysierte‹ Form eines in (a), verführt uns leicht dazu, zu meinen, jene Form sei die fundamentalere; sie zeige erst, was mit der andern gemeint sei, etc. Wir denken etwa: Wer nur die unanalysierte Form besitzt, dem geht die Analyse ab; wer aber die analysierte Form kennt, der besitze damit alles. – Aber kann ich nicht sagen, daß diesem ein Aspekt der Sache verlorengeht, so wie jenem ?
64. Denken wir uns das Spiel (48) dahin abgeändert, daß in ihm Namen nicht einfarbige Quadrate bezeichnen, sondern Rechtecke, die aus je zwei solchen Quadraten bestehen. Ein solches Rechteck, halb rot, halb grün, heiße »U«; ein Rechteck, halb grün, halb weiß, heiße »V«, etc. Könnten wir uns nicht Menschen denken, die für solche Farbenkombinationen Namen hätten, aber nicht für die einzelnen Farben? Denk an die Fälle, in denen wir sagen: »Diese Farbenzusammenstellung (die französische Trikolore etwa) hat einen ganz besonderen Charakter.«
In wiefern sind die Zeichen dieses Sprachspiels einer Analyse bedürftig? Ja, in wieweit kann das Spiel durch (48) ersetzt werden? – Es ist eben ein anderes Sprachspiel; wenn auch mit (48) verwandt.
65. Hier stoßen wir auf die große Frage, die hinter allen diesen Betrachtungen steht. – Denn man könnte mir einwenden: »Du machst dir’s leicht! Du redest von allen möglichen Sprachspielen, hast aber nirgends gesagt, was denn das Wesentliche des Sprachspiels, und also der Sprache, ist. Was allen diesen Vorgängen gemeinsam ist und sie zur Sprache, oder zu Teilen der Sprache macht. Du schenkst dir also gerade den Teil der Untersuchung, der dir selbst seinerzeit das meiste Kopfzerbrechen gemacht hat, nämlich den, die allgemeine Form des Satzes und der Sprache betreffend.«
Und das ist wahr. – Statt etwas anzugeben, was allem, was wir Sprache nennen, gemeinsam ist, sage ich, es ist diesen Erscheinungen gar nicht Eines gemeinsam, weswegen wir für alle das gleiche Wort verwenden, – sondern sie sind miteinander in vielen verschiedenen Weisen verwandt. Und dieser Verwandtschaft, oder dieser Verwandtschaften wegen nennen wir sie alle »Sprachen«. Ich will versuchen, dies zu erklären.
66. Betrachte z.B. einmal die Vorgänge, die wir »Spiele« nennen. Ich meine Brettspiele, Kartenspiele, Ballspiel, Kampfspiele, usw. Was ist allen diesen gemeinsam? – Sag nicht: »Es muß ihnen etwas gemeinsam sein, sonst hießen sie nicht ›Spiele‹« – sondern schau, ob ihnen allen etwas gemeinsam ist. – Denn wenn du sie anschaust, wirst du zwar nicht etwas sehen, was allen gemeinsam wäre, aber du wirst Ähnlichkeiten, Verwandtschaften, sehen, und zwar eine ganze Reihe. Wie gesagt: denk nicht, sondern schau! – Schau z.B. die Brettspiele an, mit ihren mannigfachen Verwandtschaften. Nun geh zu den Kartenspielen über: hier findest du viele Entsprechungen mit jener ersten Klasse, aber viele gemeinsame Züge verschwinden, andere treten auf. Wenn wir nun zu den Ballspielen übergehen, so bleibt manches Gemeinsame erhalten, aber vieles geht verloren. – Sind sie alle ›unterhaltend‹. Vergleiche Schach mit dem Mühlfahren. Oder gibt es überall ein Gewinnen und Verlieren, oder eine Konkurrenz der Spielenden? Denk an die Patiencen. In den Ballspielen gibt es Gewinnen und Verlieren; aber wenn ein Kind den Ball an die Wand wirft und wieder auffängt, so ist dieser Zug verschwunden. Schau, welche Rolle Geschick und Glück spielen. Und wie verschieden ist Geschick im Schachspiel und Geschick im Tennisspiel. Denk nun an die Reigenspiele: Hier ist das Element der Unterhaltung, aber wie viele der anderen Charakterzüge sind verschwunden! Und so können wir durch die vielen, vielen anderen Gruppen von Spielen gehen. Ähnlichkeiten auftauchen und verschwinden sehen.
Und das Ergebnis dieser Betrachtung lautet nun: Wir sehen ein kompliziertes Netz von Ähnlichkeiten, die einander übergreifen und kreuzen. Ähnlichkeiten im Großen und Kleinen.
67. Ich kann diese Ähnlichkeiten nicht besser charakterisieren als durch das Wort »Familienähnlichkeiten«; denn so übergreifen und kreuzen sich die verschiedenen Ähnlichkeiten, die zwischen den Gliedern einer Familie bestehen: Wuchs, Gesichtszüge, Augenfarbe, Gang, Temperament, etc. etc. – Und ich werde sagen: die ›Spiele‹ bilden eine Familie.
Und ebenso bilden z.B. die Zahlenarten eine Familie. Warum nennen wir etwas »Zahl«? Nun etwa, weil es eine – direkte – Verwandtschaft mit manchem hat, was man bisher Zahl genannt hat; und dadurch, kann man sagen, erhält es eine indirekte Verwandtschaft zu anderem, was wir auch so nennen. Und wir dehnen unseren Begriff der Zahl aus, wie wir beim Spinnen eines Fadens Faser an Faser drehen. Und die Stärke des Fadens liegt nicht darin, daß irgend eine Faser durch seine ganze Länge läuft, sondern darin, daß viele Fasern einander übergreifen.
Wenn aber Einer sagen wollte: »Also ist allen diesen Gebilden etwas gemeinsam, – nämlich die Disjunktion aller dieser Gemeinsamkeiten« – so würde ich antworten: hier spielst du nur mit einem Wort. Ebenso könnte man sagen: es läuft ein Etwas durch den ganzen Faden, – nämlich das lückenlose Übergreifen dieser Fasern.
68. »Gut; so ist also der Begriff der Zahl für dich erklärt als die logische Summe jener einzelnen miteinander verwandten Begriffe: Kardinalzahl, Rationalzahl, reelle Zahl, etc., und gleicherweise der Begriff des Spiels als logische Summe entsprechender Teilbegriffe.« –– Dies muß nicht sein. Denn ich kann so dem Begriff ›Zahl‹ feste Grenzen geben, d.h. das Wort »Zahl« zur Bezeichnung eines fest begrenzten Begriffs gebrauchen, aber ich kann es auch so gebrauchen, daß der Umfang des Begriffs nicht durch eine Grenze abgeschlossen ist. Und so verwenden wir ja das Wort »Spiel«. Wie ist denn der Begriff des Spiels abgeschlossen? Was ist noch ein Spiel und was ist keines mehr? Kannst du die Grenzen angeben? Nein. Du kannst welche ziehen: denn es sind noch keine gezogen. (Aber das hat dich noch nie gestört, wenn du das Wort »Spiel« angewendet hast.)
»Aber dann ist ja die Anwendung des Wortes nicht geregelt; das ›Spiel‹, welches wir mit ihm spielen, ist nicht geregelt.« –– Es ist nicht überall von Regeln begrenzt; aber es gibt ja auch keine Regel dafür z.B., wie hoch man im Tennis den Ball werfen darf, oder wie stark, aber Tennis ist doch ein Spiel und es hat auch Regeln.
69. Wie würden wir denn jemandem erklären, was ein Spiel ist? Ich glaube, wir werden ihm Spiele beschreiben, und wir könnten der Beschreibung hinzufügen: »das, und Ähnliches, nennt man ›Spiele‹«. Und wissen wir selbst denn mehr? Können wir etwa nur dem Andern nicht genau sagen, was ein Spiel ist? – Aber das ist nicht Unwissenheit. Wir kennen die Grenzen nicht, weil keine gezogen sind. Wie gesagt, wir können – für einen besondern Zweck – eine Grenze ziehen. Machen wir dadurch den Begriff erst brauchbar? Durchaus nicht! Es sei denn, für diesen besondern Zweck. So wenig, wie der das Längenmaß ›1 Schritt‹ brauchbar machte, der die Definition gab: 1 Schritt = 75 cm. Und wenn du sagen willst »Aber vorher war es doch kein exaktes Längenmaß«, so antworte ich: gut, dann war es ein unexaktes. – Obgleich du mir noch die Definition der Exaktheit schuldig bist.
70. »Aber wenn der Begriff ›Spiel‹ auf diese Weise unbegrenzt ist, so weißt du ja eigentlich nicht, was du mit ›Spiel‹ meinst.« –– Wenn ich die Beschreibung gebe: »Der Boden war ganz mit Pflanzen bedeckt«, – willst du sagen, ich weiß nicht, wovon ich rede, ehe ich nicht eine Definition der Pflanze geben kann?
Eine Erklärung dessen, was ich meine, wäre etwa eine Zeichnung und die Worte »So ungefähr hat der Boden ausgesehen«. Ich sage vielleicht auch: »genau so hat er ausgesehen«. – Also waren genau diese Gräser und Blätter, in diesen Lagen, dort? Nein, das heißt es nicht. Und kein Bild würde ich, in diesem Sinne, als das genaue anerkennen.
##
Jemand sagt mir: »Zeige den Kindern ein Spiel!« Ich lehre sie, um Geld würfeln, und der Andere sagt mir »Ich habe nicht so ein Spiel gemeint«. Mußte ihm da, als er mir den Befehl gab, der Ausschluß des Würfelspiels vorschweben?
##
71. Man kann sagen, der Begriff ›Spiel‹ ist ein Begriff mit verschwommenen Rändern. – »Aber ist ein verschwommener Begriff überhaupt ein Begriff?« – Ist eine unscharfe Photographie überhaupt ein Bild eines Menschen? Ja, kann man ein unscharfes Bild immer mit Vorteil durch ein scharfes ersetzen? Ist das unscharfe nicht oft gerade das, was wir brauchen?
Frege vergleicht den Begriff mit einem Bezirk und sagt: einen unklar begrenzten Bezirk könne man überhaupt keinen Bezirk nennen. Das heißt wohl, wir können mit ihm nichts anfangen. – Aber ist es sinnlos zu sagen: »Halte dich ungefähr hier auf«? Denk dir, ich stünde mit einem Andern auf einem Platz und sagte dies. Dabei werde ich nicht einmal irgend eine Grenze ziehen, sondern etwa mit der Hand eine zeigende Bewegung machen – als zeigte ich ihm einen bestimmten Punkt. Und gerade so erklärt man etwa, was ein Spiel ist. Man gibt Beispiele und will, daß sie in einem gewissen Sinn verstanden werden. – Aber mit diesem Ausdruck meine ich nicht: er solle nun in diesen Beispielen das Gemeinsame sehen, welches ich – aus irgend einem Grunde – nicht aussprechen konnte. Sondern: er solle diese Beispiele nun in bestimmter Weise verwenden. Das Exemplifizieren ist hier nicht ein indirektes Mittel der Erklärung, – in Ermanglung eines Bessern. Denn, mißverstanden kann auch jede allgemeine Erklärung werden. So spielen wir eben das Spiel. (Ich meine das Sprachspiel mit dem Wort »Spiel«.)
72. Das Gemeinsame sehen. Nimm an, ich zeige jemand verschiedene bunte Bilder, und sage: »Die Farbe, die du in allen siehst, heißt ›Ocker‹.« – Das ist eine Erklärung, die verstanden wird, indem der Andere aufsucht und sieht, was jenen Bildern gemeinsam ist. Er kann dann auf das Gemeinsame blicken, darauf zeigen.
Vergleiche damit: Ich zeige ihm Figuren verschiedener Form, alle in der gleichen Farbe gemalt und sage: »Was diese miteinander gemein haben, heißt ›Ocker‹«.
Und vergleiche damit: Ich zeige ihm Muster verschiedener Schattierungen von Blau und sage: »Die Farbe, die allen gemeinsam ist, nenne ich ›Blau‹«.
73. Wenn Einer mir den Namen der Farben erklärt, indem er auf Muster zeigt und sagt »Diese Farbe heißt ›Blau‹, diese ›Grün‹,...«, so kann dieser Fall in vieler Hinsicht dem verglichen werden, daß er mir eine Tabelle an die Hand gibt, in der unter den Mustern von Farben die Wörter stehen. – Wenn auch dieser Vergleich in mancher Weise irreführen kann. – Man ist nun geneigt, den Vergleich auszudehnen: Die Erklärung verstanden haben, heißt, einen Begriff des Erklärten im Geiste besitzen, und d.i. ein Muster, oder Bild. Zeigt man mir nun verschiedene Blätter und sagt: »Das nennt man ›Blatt‹«, so erhalte ich einen Begriff der Blattform, ein Bild von ihr im Geiste. – Aber wie schaut denn das Bild eines Blattes aus, das keine bestimmte Form zeigt, sondern ›das, was allen Blattformen gemeinsam ist‹? Welchen Farbton hat das ›Muster in meinem Geiste‹ der Farbe Grün – dessen, was allen Tönen von Grün gemeinsam ist?
»Aber könnte es nicht solche ›allgemeine‹ Muster geben? Etwa ein Blattschema, oder ein Muster von reinem Grün?« – Gewiß! Aber, daß dieses Schema als Schema verstanden wird, und nicht als die Form eines bestimmten Blattes, und daß ein Täfelchen von reinem Grün als Muster alles dessen verstanden wird, was grünlich ist, und nicht als Muster für reines Grün – das liegt wieder in der Art der Anwendung dieser Muster.
Frage dich: Welche Gestalt muß das Muster der Farbe Grün haben? Soll es viereckig sein? oder würde es dann das Muster für grüne Vierecke sein? – Soll es also ›unregelmäßig‹ geformt sein? Und was verhindert uns, es dann nur als Muster der unregelmäßigen Form anzusehen – d.h. zu verwenden?
74. Hierher gehört auch der Gedanke, daß der, welcher dieses Blatt als Muster ›der Blattform im allgemeinem‹ ansieht, es anders sieht als der, welcher es etwa als Muster für diese bestimmte Form betrachtet. Nun, das könnte ja so sein – obwohl es nicht so ist – , denn es würde nur besagen, daß erfahrungsgemäß der, welcher das Blatt in bestimmter Weise sieht, es dann so und so, oder den und den Regeln gemäß, verwendet. Es gibt natürlich ein so und anders Sehen; und es gibt auch Fälle, in denen der, der ein Muster so sieht, es im allgemeinen in dieser Weise verwenden wird, und wer es anders sieht, in anderer Weise. Wer, z.B., die schematische Zeichnung eines Würfels als ebene Figur sieht, bestehend aus einem Quadrat und zwei Rhomben, der wird den Befehl »Bringe mir so etwas!« vielleicht anders ausführen als der, welcher das Bild räumlich sieht.
75. Was heißt es: wissen, was ein Spiel ist? Was heißt es, es wissen und es nicht sagen können? Ist dieses Wissen irgendein Äquivalent einer nicht ausgesprochenen Definition? So daß, wenn sie ausgesprochen würde, ich sie als den Ausdruck meines Wissens anerkennen könnte? Ist nicht mein Wissen, mein Begriff vom Spiel, ganz in den Erklärungen ausgedrückt, die ich geben könnte? Nämlich darin, daß ich Beispiele von Spielen verschiedener Art beschreibe; zeige, wie man nach Analogie dieser auf alle möglichen Arten andere Spiele konstruieren kann; sage, daß ich das und das wohl kaum mehr ein Spiel nennen würde; und dergleichen mehr.
76. Wenn Einer eine scharfe Grenze zöge, so könnte ich sie nicht als die anerkennen, die ich auch schon immer ziehen wollte, oder im Geist gezogen habe. Denn ich wollte gar keine ziehen. Man kann dann sagen: sein Begriff ist nicht der gleiche wie der meine, aber ihm verwandt. Und die Verwandtschaft ist die zweier Bilder, deren eines aus unscharf begrenzten Farbflecken, das andere aus ähnlich geformten und verteilten, aber scharf begrenzten, besteht. Die Verwandtschaft ist dann ebenso unleugbar wie die Verschiedenheit.
77. Und wenn wir diesen Vergleich noch etwas weiter führen, so ist es klar, daß der Grad, bis zu welchem das scharfe Bild dem verschwommenen ähnlich sein kann, vom Grade der Unschärfe des zweiten abhängt. Denn denk dir, du solltest zu einem verschwommenen Bild ein ihm ›entsprechendes‹ scharfes entwerfen. In jenem ist ein unscharfes rotes Rechteck; du setzt dafür ein scharfes. Freilich – es ließen sich ja mehrere solche scharfe Rechtecke ziehen, die dem unscharfen entsprächen. – Wenn aber im Original die Farben ohne die Spur einer Grenze ineinanderfließen, – wird es dann nicht eine hoffnungslose Aufgabe werden, ein dem verschwommenen entsprechendes scharfes Bild zu zeichnen? Wirst du dann nicht sagen müssen: »Hier könnte ich ebenso gut einen Kreis wie ein Rechteck oder eine Herzform zeichnen; es fließen ja alle Farben durcheinander. Es stimmt alles; und nichts.« – Und in dieser Lage befindet sich z.B. der, der in der Ästhetik oder Ethik nach Definitionen sucht, die unseren Begriffen entsprechen.
Frage dich in dieser Schwierigkeit immer: Wie haben wir denn die Bedeutung dieses Wortes (»gut« z.B.) gelernt? An was für Beispielen; in welchen Sprachspielen? (Du wirst dann leichter sehen, daß das Wort eine Familie von Bedeutungen haben muß.)
78. Vergleiche: wissen und sagen:
wieviele m hoch der Mont-Blanc ist –
wie das Wort »Spiel« gebraucht wird –
wie eine Klarinette klingt.
Wer sich wundert, daß man etwas wissen könne, und nicht sagen, denkt vielleicht an einen Fall wie den ersten. Gewiß nicht an einen wie den dritten.
79. Betrachte dieses Beispiel: Wenn man sagt »Moses hat nicht existiert«, so kann das Verschiedenerlei bedeuten. Es kann heißen: die Israeliten haben nicht einen Führer gehabt, als sie aus Ägypten auszogen –– oder: ihr Führer hat nicht Moses geheißen –– oder: es hat keinen Menschen gegeben, der alles das vollbracht hat, was die Bibel von Moses berichtet –– oder etc. etc. – Nach Russell können wir sagen: der Name »Moses« kann durch verschiedene Beschreibungen definiert werden. Z.B. als: »der Mann, welcher die Israeliten durch die Wüste geführt hat«, »der Mann, welcher zu dieser Zeit und an diesem Ort gelebt hat und damals ›Moses‹ genannt wurde«, »der Mann, welcher als Kind von der Tochter Pharaos aus dem Nil gezogen wurde«, etc. Und je nachdem wir die eine oder die andere Definition annehmen, bekommt der Satz »Moses hat existiert« einen andern Sinn, und ebenso jeder andere Satz, der von Moses handelt. – Und wenn man uns sagt »N hat nicht existiert«, fragen wir auch: »Was meinst du? Willst du sagen, daß ...., oder daß .…, etc.?«
Aber wenn ich nun eine Aussage über Moses mache, – bin ich immer bereit, irgend eine dieser Beschreibungen für »Moses« zu setzen? Ich werde etwa sagen: Unter »Moses« verstehe ich den Mann, der getan hat, was die Bibel von Moses berichtet, oder doch vieles davon. Aber wievieles? Habe ich mich entschieden, wieviel sich als falsch erweisen muß, damit ich meinen Satz als falsch aufgebe? Hat also der Name »Moses« für mich einen festen und eindeutig bestimmten Gebrauch in allen möglichen Fällen? – Ist es nicht so, daß ich sozusagen eine ganze Reihe von Stützen in Bereitschaft habe und bereit bin, mich auf eine zu stützen, wenn mir die andere entzogen werden sollte, und umgekehrt? –– Betrachte noch einen andern Fall. Wenn ich sage »N ist gestorben«, so kann es mit der Bedeutung des Namens »N« etwa diese Bewandtnis haben: Ich glaube, daß ein Mensch gelebt hat, den ich (1) dort und dort gesehen habe, der (2) so und so ausgeschaut hat (Bilder), (3) das und das getan hat und (4) in der bürgerlichen Welt diesen Namen »N« führt. – Gefragt, was ich unter »N« verstehe, würde ich alles das, oder einiges davon, und bei verschiedenen Gelegenheiten Verschiedenes, aufzählen. Meine Definition von »N« wäre also etwa: »der Mann, von dem alles das stimmt«. – Aber wenn sich nun etwas davon als falsch erwiese! – Werde ich bereit sein, den Satz »N ist gestorben« für falsch zu erklären, – auch wenn nur etwas mir nebensächlich Scheinendes sich als falsch herausstellt? Wo aber ist die Grenze des Nebensächlichen? – Hätte ich in so einem Fall eine Erklärung des Namens gegeben, so wäre ich nun bereit, sie abzuändern.
Und das kann man so ausdrücken: Ich gebrauche den Namen »N« ohne feste Bedeutung. (Aber das tut seinem Gebrauch so wenig Eintrag, wie dem eines Tisches, daß er auf vier Beinen ruht, statt auf dreien, und daher unter Umständen wackelt.)
Soll man sagen, ich gebrauche ein Wort, dessen Bedeutung ich nicht kenne, rede also Unsinn? – Sage, was du willst, solange dich das nicht verhindert, zu sehen, wie es sich verhält. (Und wenn du das siehst, wirst du manches nicht sagen.)
(Das Schwanken wissenschaftlicher Definitionen: Was heute als erfahrungsmäßige Begleiterscheinung des Phänomens A gilt, wird morgen zur Definition von »A« benützt.)
80. Ich sage: »Dort steht ein Sessel«. Wie, wenn ich hingehe und ihn holen will, und er entschwindet plötzlich meinem Blick? –– »Also war es kein Sessel, sondern irgend eine Täuschung.« –– Aber in ein paar Sekunden sehen wir ihn wieder und können ihn angreifen, etc. –– »Also war der Sessel doch da und sein Verschwinden war irgend eine Täuschung.« –– Aber nimm an, nach einer Zeit verschwindet er wieder, – oder scheint zu verschwinden. Was sollen wir nun sagen? Hast du für solche Fälle Regeln bereit, – die sagen, ob man so etwas noch »Sessel« nennen darf? Aber gehen sie uns beim Gebrauch des Wortes »Sessel« ab; und sollen wir sagen, daß wir mit diesem Wort eigentlich keine Bedeutung verbinden, da wir nicht für alle Möglichkeiten seiner Anwendung mit Regeln ausgerüstet sind?
81. F. P. Ramsey hat einmal im Gespräch mit mir betont, die Logik sei eine ›normative Wissenschaft‹. Genau welche Idee ihm dabei vorschwebte, weiß ich nicht; sie war aber zweifellos eng verwandt mit der, die mir erst später aufgegangen ist: daß wir nämlich in der Philosophie den Gebrauch der Wörter oft mit Spielen, Kalkülen nach festen Regeln, vergleichen, aber nicht sagen können, wer die Sprache gebraucht, müsse ein solches Spiel spielen. – – Sagt man nun aber, daß unser sprachlicher Ausdruck sich solchen Kalkülen nur nähert, so steht man damit unmittelbar am Rande eines Mißverständnisses. Denn so kann es scheinen, als redeten wir in der Logik von einer idealen Sprache. Als wäre unsre Logik eine Logik, gleichsam, für den luftleeren Raum. – Während die Logik doch nicht von der Sprache – bzw. vom Denken – handelt in dem Sinne, wie eine Naturwissenschaft von einer Naturerscheinung, und man höchstens sagen kann, wir konstruierten ideale Sprachen. Aber hier wäre das Wort »ideal« irreführend, denn das klingt, als wären diese Sprachen besser, vollkommener, als unsere Umgangssprache; und als brauchte es den Logiker, damit er den Menschen endlich zeigt, wie ein richtiger Satz ausschaut.
All das kann aber erst dann im rechten Licht erscheinen, wenn man über die Begriffe des Verstehens, Meinens und Denkens größere Klarheit gewonnen hat. Denn dann wird es auch klar werden, was uns dazu verleiten kann (und mich verleitet hat) zu denken, daß, wer einen Satz ausspricht und ihn meint, oder versteht, damit einen Kalkül betreibt nach bestimmten Regeln.
82. Was nenne ich ›die Regel, nach der er vorgehe‹? – Die Hypothese, die seinen Gebrauch der Worte, den wir beobachten, zufriedenstellend beschreibt; oder die Regel, die er beim Gebrauch der Zeichen nachschlägt; oder, die er uns zur Antwort gibt, wenn wir ihn nach seiner Regel fragen? – Wie aber, wenn die Beobachtung keine Regel klar erkennen läßt, und die Frage keine zu Tage fördert? – Denn er gab mir zwar auf meine Frage, was er unter »N« verstehe, eine Erklärung, war aber bereit, diese Erklärung zu widerrufen und abzuändern. – Wie soll ich also die Regel bestimmen, nach der er spielt? Er weiß sie selbst nicht. – Oder richtiger: Was soll der Ausdruck »Regel, nach welcher er vorgeht« hier noch besagen?
83. Steckt uns da nicht die Analogie der Sprache mit dem Spiel ein Licht auf? Wir können uns doch sehr wohl denken, daß sich Menschen auf einer Wiese damit unterhielten, mit einem Ball zu spielen, so zwar, daß sie verschiedene bestehende Spiele anfingen, manche nicht zu Ende spielten, dazwischen den Ball planlos in die Höhe würfen, einander im Scherz mit dem Ball nachjagen und bewerfen, etc. Und nun sagt Einer: Die ganze Zeit hindurch spielen die Leute ein Ballspiel, und richten sich daher bei jedem Wurf nach bestimmten Regeln.
Und gibt es nicht auch den Fall, wo wir spielen und – ›make up the rules as we go along‹? Ja auch den, in welchem wir sie abandern – as we go along.
84. Ich sagte von der Anwendung eines Wortes: sie sei nicht überall von Regeln begrenzt. Aber wie schaut denn ein Spiel aus, das überall von Regeln begrenzt ist? dessen Regeln keinen Zweifel eindringen lassen; ihm alle Löcher verstopfen. – Können wir uns nicht eine Regel denken, die die Anwendung der Regel regelt? Und einen Zweifel, den jene Regel behebt – und so fort?
Aber das sagt nicht, daß wir zweifeln, weil wir uns einen Zweifel denken können. Ich kann mir sehr wohl denken, daß jemand jedesmal vor dem Öffnen seiner Haustür zweifelt, ob sich hinter ihr nicht ein Abgrund aufgetan hat, und daß er sich darüber vergewissert, eh’ er durch die Tür tritt (und es kann sich einmal erweisen, daß er recht hatte) – aber deswegen zweifle ich im gleichen Falle doch nicht.
85. Eine Regel steht da, wie ein Wegweiser. – Läßt er keinen Zweifel offen über den Weg, den ich zu gehen habe? Zeigt er, in welche Richtung ich gehen soll, wenn ich an ihm vorbei bin; ob der Straße nach, oder dem Feldweg, oder querfeldein? Aber wo steht, in welchem Sinne ich ihm zu folgen habe; ob in der Richtung der Hand, oder (z.B.) in der entgegengesetzten? – Und wenn statt eines Wegweisers eine geschlossene Kette von Wegweisern stünde, oder Kreidestriche auf dem Boden liefen, – gibt es für sie nur eine Deutung? – Also kann ich sagen, der Wegweiser läßt doch keinen Zweifel offen. Oder vielmehr: er läßt manchmal einen Zweifel offen, manchmal nicht. Und dies ist nun kein philosophischer Satz mehr, sondern ein Erfahrungssatz.
86. Ein Sprachspiel wie (2) werde mit Hilfe einer Tabelle gespielt. Die Zeichen, die A dem B gibt, seien nun Schriftzeichen. B hat eine Tabelle; in der ersten Spalte stehen die Schriftzeichen, die im Spiel gebraucht werden, in der zweiten, Bilder von Bausteinformen. A zeigt dem B ein solches Schriftzeichen; B sucht es in der Tabelle auf, blickt auf das gegenüberliegende Bild, etc. Die Tabelle ist also eine Regel, nach der er sich beim Ausführen der Befehle richtet. – Das Aufsuchen des Bildes in der Tabelle lernt man durch Abrichtung, und ein Teil dieser Abrichtung besteht etwa darin, daß der Schüler lernt, in der Tabelle mit dem Finger horizontal von links nach rechts zu fahren; also lernt, sozusagen eine Reihe horizontaler Striche zu ziehen.
Denk dir, es würden nun verschiedene Arten eingeführt eine Tabelle zu lesen; nämlich einmal, wie oben, nach dem Schema:

ein andermal nach diesem Schema:
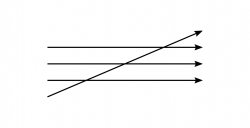
oder einem andern. – So ein Schema werde der Tabelle beigefügt als Regel, wie sie zu gebrauchen sei.
Können wir uns nun nicht weitere Regeln zur Erklärung dieser vorstellen? und war anderseits jene erste Tabelle unvollständig ohne das Schema der Pfeile? Und sind es die andern Tabellen ohne ihr Schema?
87. Nimm an, ich erkläre: »Unter ›Moses‹ verstehe ich den Mann, wenn es einen solchen gegeben hat, der die Israeliten aus Ägypten geführt hat, wie immer er damals geheißen hat und was immer er sonst getan, oder nicht getan haben mag«. – Aber über die Wörter dieser Erklärung sind ähnliche Zweifel möglich wie die über den Namen »Moses« (was nennst du »Ägypten«, wen »die Israeliten«, etc.?). Ja, diese Fragen kommen auch nicht zu einem Ende, wenn wir bei Wörtern wie »rot«, »dunkel«, »süß«, angelangt wären. – »Aber wie hilft mir dann eine Erklärung zum Verständnis, wenn sie doch nicht die letzte ist? Die Erklärung ist dann ja nie beendet; ich verstehe also noch immer nicht, und nie, was er meint!« – Als hinge eine Erklärung, gleichsam, in der Luft, wenn nicht eine andere sie stütze. Während eine Erklärung zwar auf einer andern, die man gegeben hat, ruhen kann, aber keine einer anderen bedarf – es sei denn, daß wir sie benötigen, um ein Mißverständnis zu vermeiden. Man könnte sagen: Eine Erklärung dient dazu, ein Mißverständnis zu beseitigen, oder zu verhüten –– also eines, das ohne die Erklärung eintreten würde; aber nicht: jedes, welches ich mir vorstellen kann.
Es kann leicht so scheinen, als zeigte jeder Zweifel nur eine vorhandene Lücke im Fundament; so daß ein sicheres Verständnis nur dann möglich ist, wenn wir zuerst an allem zweifeln, woran gezweifelt werden kann, und dann alle diese Zweifel beheben.
Der Wegweiser ist in Ordnung, – wenn er, unter normalen Verhältnissen, seinen Zweck erfüllt.
88. Wenn ich Einem sage »Halte dich ungefähr hier auf!« – kann denn diese Erklärung nicht vollkommen funktionieren? Und kann jede andere nicht auch versagen?
»Aber ist die Erklärung nicht doch unexakt?« – Doch; warum soll man sie nicht »unexakt« nennen? Verstehen wir aber nur, was »unexakt« bedeutet! Denn es bedeutet nun nicht »unbrauchbar«. Und überlegen wir uns doch, was wir, im Gegensatz zu dieser Erklärung, eine »exakte« Erklärung nennen! Etwa das Abgrenzen eines Bezirks durch einen Kreidestrich? Da fällt uns gleich ein, daß der Strich eine Breite hat. Exakter wäre also eine Farbgrenze. Aber hat denn diese Exaktheit hier noch eine Funktion; läuft sie nicht leer? Und wir haben ja auch noch nicht bestimmt, was als Überschreiten dieser scharfen Grenze gelten soll; wie, mit welchen Instrumenten, es festzustellen ist. Usw.
Wir verstehen, was es heißt: eine Taschenuhr auf die genaue Stunde stellen, oder, sie richten, daß sie genau geht. Wie aber, wenn man fragte: Ist diese Genauigkeit eine ideale Genauigkeit, oder wie weit nähert sie sich ihr? – wir können freilich von Zeitmessungen reden, bei welchen es eine andere und, wie wir sagen würden, größere Genauigkeit gibt als bei der Zeitmessung mit der Taschenuhr. Wo die Worte »die Uhr auf die genaue Stunde stellen« eine andere, wenn auch verwandte, Bedeutung haben, und ›die Uhr ablesen‹ ein anderer Vorgang ist, etc. – Wenn ich nun jemandem sage: »Du solltest pünktlicher zum Essen kommen; du weißt, daß es genau um ein Uhr anfängt« – ist hier von Genauigkeit eigentlich nicht die Rede? weil man sagen kann: »Denk an die Zeitbestimmung im Laboratorium, oder auf der Sternwarte; da siehst du, was ›Genauigkeit‹ bedeutet.«
»Unexakt«, das ist eigentlich ein Tadel, und »exakt« ein Lob. Und das heißt doch: das Unexakte erreicht sein Ziel nicht so vollkommen wie das Exaktere. Da kommt es also auf das an, was wir »das Ziel« nennen. Ist es unexakt, wenn ich den Abstand der Sonne von uns nicht auf 1 m genau angebe; und dem Tischler die Breite des Tisches nicht auf 0,001 mm?
Ein Ideal der Genauigkeit ist nicht vorgesehen; wir wissen nicht, was wir uns darunter vorstellen sollen – es sei denn, du selbst setzt fest, was so genannt werden soll. Aber es wird dir schwer werden, so eine Festsetzung zu treffen; eine, die dich befriedigt.
89. Wir stehen mit diesen Überlegungen an dem Ort, wo das Problem steht: Inwiefern ist die Logik etwas Sublimes?
Denn es schien, daß ihr eine besondere Tiefe – allgemeine Bedeutung – zukomme. Sie liege, so schien es, am Grunde aller Wissenschaften. – Denn die logische Betrachtung erforscht das Wesen aller Dinge. Sie will den Dingen auf den Grund sehen, und soll sich nicht um das So oder So des tatsächlichen Geschehens kümmern. –– Sie entspringt nicht einem Interesse für Tatsachen des Naturgeschehens, noch dem Bedürfnisse, kausale Zusammenhänge zu erfassen, sondern einem Streben, das Fundament, oder Wesen, alles Erfahrungsmäßigen zu verstehen. Nicht aber, als sollten wir dazu neue Tatsachen aufspüren: es ist vielmehr für unsere Untersuchung wesentlich, daß wir nichts Neues mit ihr lernen wollen. Wir wollen etwas verstehen, was schon offen vor unsern Augen liegt. Denn das scheinen wir, in irgendeinem Sinne, nicht zu verstehen.
Augustinus (Conf. XI/14): »quid est ergo tempus? si nemo ex me quaerat scio; si quaerenti explicare velim, nescio.« – Dies könnte man nicht von einer Frage der Naturwissenschaft sagen (etwa der nach dem spezifischen Gewicht des Wasserstoffs). Das, was man weiß, wenn uns niemand fragt, aber nicht mehr weiß, wenn wir es erklären sollen, ist etwas, worauf man sich besinnen muß. (Und offenbar etwas, worauf man sich aus irgendeinem Grunde schwer besinnt.)
90. Es ist uns, als müßten wir die Erscheinungen durchschauen: unsere Untersuchung aber richtet sich nicht auf die Erscheinungen, sondern, wie man sagen könnte, auf die ›Möglichkeiten‹ der Erscheinungen. Wir besinnen uns, heißt das, auf die Art der Aussagen, die wir über die Erscheinungen machen. Daher besinnt sich auch Augustinus auf die verschiedenen Aussagen, die man über die Dauer von Ereignissen, über ihre Vergangenheit, Gegenwart, oder Zukunft macht. (Dies sind natürlich nicht philosophische Aussagen über die Zeit, Vergangenheit, Gegenwart und Zukunft.)
Unsere Betrachtung ist daher eine grammatische. Und diese Betrachtung bringt Licht in unser Problem, indem sie Mißverständnisse wegräumt. Mißverständnisse, die den Gebrauch von Worten betreffen; hervorgerufen, unter anderem, durch gewisse Analogien zwischen den Ausdrucksformen in verschiedenen Gebieten unserer Sprache. – Manche von ihnen lassen sich beseitigen, indem man eine Ausdrucksform durch eine andere ersetzt; dies kann man ein »Analysieren« unsrer Ausdrucksformen nennen, denn der Vorgang hat manchmal Ähnlichkeit mit einem Zerlegen.
91. Nun aber kann es den Anschein gewinnen, als gäbe es so etwas wie eine letzte Analyse unserer Sprachformen, also eine vollkommen zerlegte Form des Ausdrucks. D.h.: als seien unsere gebräuchlichen Ausdrucksformen, wesentlich, noch unanalysiert; als sei in ihnen etwas verborgen, was ans Licht zu befördern ist. Ist dies geschehen, so sei der Ausdruck damit vollkommen geklärt und unsre Aufgabe gelöst.
Man kann das auch so sagen: Wir beseitigen Mißverständnisse, indem wir unsern Ausdruck exakter machen: aber es kann nun so scheinen, als ob wir einem bestimmten Zustand, der vollkommenen Exaktheit, zustreben; und als wäre das das eigentliche Ziel unserer Untersuchung.
92. Dies drückt sich aus in der Frage nach dem Wesen der Sprache, des Satzes, des Denkens. – Denn wenn wir auch in unsern Untersuchungen das Wesen der Sprache – ihre Funktion, ihren Bau – zu verstehen trachten, so ist es doch nicht das, was diese Frage im Auge hat. Denn sie sieht in dem Wesen nicht etwas, was schon offen zutage liegt und was durch Ordnen übersichtlich wird. Sondern etwas, was unter der Oberfläche liegt. Etwas, was im Innern liegt, was wir sehen, wenn wir die Sache durchschauen, und was eine Analyse hervorgraben soll.
›Das Wesen ist uns verborgen‹. das ist die Form, die unser Problem nun annimmt. Wir fragen: »Was ist die Sprache?«, »Was ist der Satz?«. Und die Antwort auf diese Fragen ist ein für allemal zu geben; und unabhängig von jeder künftigen Erfahrung.
93. Einer könnte sagen »Ein Satz, das ist das Alltäglichste von der Welt«, und der Andre: »Ein Satz – das ist etwas sehr Merkwürdiges!« –– Und dieser kann nicht: einfach nachschauen, wie Sätze funktionieren. Weil die Formen unserer Ausdrucksweise, die Sätze und das Denken betreffend, ihm im Wege stehen.
Warum sagen wir, der Satz sei etwas Merkwürdiges? Einerseits, wegen der ungeheuren Bedeutung, die ihm zukommt. (Und das ist richtig.) Anderseits verführt uns diese Bedeutung und ein Mißverstehen der Sprachlogik dazu, daß wir meinen, der Satz müsse etwas Außerordentliches, ja Einzigartiges, leisten. – Durch ein Mißverständnis erscheint es uns, als tue der Satz etwas Seltsames.
94. ›Der Satz, ein merkwürdiges Ding!‹: darin liegt schon die Sublimierung der ganzen Darstellung. Die Tendenz, ein reines Mittelwesen anzunehmen zwischen dem Satzzeichen und den Tatsachen. Oder auch, das Satzzeichen selber reinigen, sublimieren, zu wollen. – Denn, daß es mit gewöhnlichen Dingen zugeht, das zu sehen, verhindern uns auf mannigfache Weise unsere Ausdrucksformen, indem sie uns auf die Jagd nach Chimären schicken.
95. »Denken muß etwas Einzigartiges sein.« Wenn wir sagen, meinen, daß es sich so und so verhält, so halten wir mit dem, was wir meinen, nicht irgendwo vor der Tatsache: sondern meinen, daß das und das – so und so – ist. – Man kann aber dieses Paradox (welches ja die Form einer Selbstverständlichkeit hat) auch so ausdrücken: Man kann denken, was nicht der Fall ist.
96. Der besondern Täuschung, die hier gemeint ist, schließen sich, von verschiedenen Seiten, andere an. Das Denken, die Sprache, erscheint uns nun als das einzigartige Korrelat, Bild, der Welt. Die Begriffe: Satz, Sprache, Denken, Welt, stehen in einer Reihe hintereinander, jeder dem andern äquivalent. (Wozu aber sind diese Wörter nun zu brauchen? Es fehlt das Sprachspiel, worin sie anzuwenden sind.)
97. Das Denken ist mit einem Nimbus umgeben. – Sein Wesen, die Logik, stellt eine Ordnung dar, und zwar die Ordnung a priori der Welt, d.i. die Ordnung der Möglichkeiten, die Welt und Denken gemeinsam sein muß. Diese Ordnung aber, scheint es, muß höchst einfach sein. Sie ist vor aller Erfahrung; muß sich durch die ganze Erfahrung hindurchziehen; ihr selbst darf keine erfahrungsmäßige Trübe oder Unsicherheit anhaften. –– Sie muß vielmehr vom reinsten Kristall sein. Dieser Kristall aber erscheint nicht als eine Abstraktion; sondern als etwas Konkretes, ja als das Konkreteste, gleichsam Härteste. (Log. Phil. Abh. 5.5563.)
Wir sind in der Täuschung, das Besondere, Tiefe, das uns Wesentliche unserer Untersuchung liege darin, daß sie das unvergleichliche Wesen der Sprache zu begreifen trachtet. D.i., die Ordnung, die zwischen den Begriffen des Satzes, Wortes, Schließens, der Wahrheit, der Erfahrung, usw. besteht. Diese Ordnung ist eine Über-Ordnung zwischen – sozusagen – Über-Begriffen. Während doch die Worte »Sprache«, »Erfahrung«, »Welt«, wenn sie eine Verwendung haben, eine so niedrige haben müssen, wie die Worte »Tisch«, »Lampe«, »Tür«.
98. Einerseits ist klar, daß jeder Satz unsrer Sprache ›in Ordnung ist, wie er ist‹. D.h., daß wir nicht ein Ideal anstreben: Als hätten unsere gewöhnlichen, vagen Sätze noch keinen ganz untadelhaften Sinn und eine vollkommene Sprache wäre von uns erst zu konstruieren. – Anderseits scheint es klar: Wo Sinn ist, muß vollkommene Ordnung sein. –– Also muß die vollkommene Ordnung auch im vagsten Satze stecken.
99. Der Sinn des Satzes – möchte man sagen – kann freilich dies oder das offen lassen, aber der Satz muß doch einen bestimmten Sinn haben. Ein unbestimmter Sinn, – das wäre eigentlich gar kein Sinn. – Das ist wie: Eine unscharfe Begrenzung, das ist eigentlich gar keine Begrenzung. Man denkt da etwa so: Wenn ich sage »ich habe den Mann fest im Zimmer eingeschlossen – nur eine Tür ist offen geblieben« – so habe ich ihn eben gar nicht eingeschlossen. Er ist nur zum Schein eingeschlossen. Man wäre geneigt, hier zu sagen: »also hast du damit gar nichts getan«. Eine Umgrenzung, die ein Loch hat, ist so gut, wie gar keine. – Aber ist das denn wahr?
100. »Es ist doch kein Spiel, wenn es eine Vagheit in den Regeln gibt.« – Aber ist es dann kein Spiel? – »Ja, vielleicht wirst du es Spiel nennen, aber es ist doch jedenfalls kein vollkommenes Spiel.« D.h.: es ist doch dann verunreinigt, und ich interessiere mich nun für dasjenige, was hier verunreinigt wurde. – Aber ich will sagen: Wir mißverstehen die Rolle, die das Ideal in unsrer Ausdrucksweise spielt. D.h.: auch wir würden es ein Spiel nennen, nur sind wir vom Ideal geblendet und sehen daher nicht deutlich die wirkliche Anwendung des Wortes »Spiel«.