Note dettate a G.E. Moore in Norvegia: Difference between revisions
No edit summary |
No edit summary |
||
| Line 65: | Line 65: | ||
1) Prendi ϕ''x''. Vogliamo spiegare il significato di “in ‘ϕ''x''’ una ''cosa'' simbolizza”. L’analisi è: | 1) Prendi ϕ''x''. Vogliamo spiegare il significato di “in ‘ϕ''x''’ una ''cosa'' simbolizza”. L’analisi è: | ||
{{p indent|(∃''y'') . ''y'' simbolizza . ''y'' <nowiki>=</nowiki> “''x''” . “ϕ''x''”}} | |||
[“''x''” è il nome di ''y'': “ϕ''x''” = “‘ϕ’ è alla sinistra di ‘''x''’” e ''dice'' ϕ''x''.] | [“''x''” è il nome di ''y'': “ϕ''x''” = “‘ϕ’ è alla sinistra di ‘''x''’” e ''dice'' ϕ''x''.] | ||
| Line 87: | Line 87: | ||
2) Qui la questione può essere esplicata nel modo seguente. Prendi ϕ''a'' e ϕ''A'': e chiediti che cosa si intende dicendo “c’è una cosa in ϕ''a'' e un complesso in ϕ''A''”? | 2) Qui la questione può essere esplicata nel modo seguente. Prendi ϕ''a'' e ϕ''A'': e chiediti che cosa si intende dicendo “c’è una cosa in ϕ''a'' e un complesso in ϕ''A''”? | ||
{{p indent|1) significa: (∃''x'') . ϕ''x'' . ''x'' <nowiki>=</nowiki> ''A''}} | |||
{{p indent|2) significa: (∃''x'', ψξ) . ϕ''A'' <nowiki>=</nowiki> ψ''x'' . ϕ''x''.<!--<ref>ξ è il simbolo di Frege per una ''Argumentstelle'', per mostrare che ψ è un ''Funktionsbuchstabe''. [''Edd.'']</ref>-->}} | |||
''Uso di proposizioni logiche''. Puoi trovarne una così complicata da non accorgerti, osservandola, che è una tautologia; ma hai mostrato che può essere derivata con certe operazioni da certe altre proposizioni secondo la nostra regola per la costruzione delle tautologie; e dunque sei in grado di vedere che una cosa segue da un’altra, mentre altrimenti non saresti stato capace di vederlo. Per esempio, se la nostra tautologia è della forma ''p'' ⊃ ''q'' puoi vedere che ''q'' segue da ''p''; e avanti così. | ''Uso di proposizioni logiche''. Puoi trovarne una così complicata da non accorgerti, osservandola, che è una tautologia; ma hai mostrato che può essere derivata con certe operazioni da certe altre proposizioni secondo la nostra regola per la costruzione delle tautologie; e dunque sei in grado di vedere che una cosa segue da un’altra, mentre altrimenti non saresti stato capace di vederlo. Per esempio, se la nostra tautologia è della forma ''p'' ⊃ ''q'' puoi vedere che ''q'' segue da ''p''; e avanti così. | ||
| Line 207: | Line 207: | ||
ϕ non potrà mai stare a sinistra del simbolo di una proprietà (o in qualsiasi altra relazione con esso). Perché il simbolo di una proprietà, per esempio ψ''x'', è ''che'' ψ sta alla sinistra di una forma-nome, e un altro simbolo ϕ non potrà mai stare a sinistra di un tale ''fatto'': se potesse, disporremmo di un linguaggio illogico, il che è impossibile. | ϕ non potrà mai stare a sinistra del simbolo di una proprietà (o in qualsiasi altra relazione con esso). Perché il simbolo di una proprietà, per esempio ψ''x'', è ''che'' ψ sta alla sinistra di una forma-nome, e un altro simbolo ϕ non potrà mai stare a sinistra di un tale ''fatto'': se potesse, disporremmo di un linguaggio illogico, il che è impossibile. | ||
{{p indent|''p'' è falso <nowiki>=</nowiki> ~(''p'' è vero) Def.}} | |||
È molto importante che le relazioni logiche apparenti ∨, ⊃, etc. necessitino di parentesi, punti, etc., ovverosia che abbiano “raggi d’azione”; ciò basta a mostrare che esse non sono relazioni. Questo fatto è stato trascurato proprio per la sua universalità – che è proprio ciò che lo rende tanto importante.<!-- [''Cfr.'' 5.461.]--> | È molto importante che le relazioni logiche apparenti ∨, ⊃, etc. necessitino di parentesi, punti, etc., ovverosia che abbiano “raggi d’azione”; ciò basta a mostrare che esse non sono relazioni. Questo fatto è stato trascurato proprio per la sua universalità – che è proprio ciò che lo rende tanto importante.<!-- [''Cfr.'' 5.461.]--> | ||
Revision as of 17:05, 21 May 2023
Ludwig Wittgenstein
Note dettate a G.E. Moore in Norvegia
Traduzione di Luca Bernardi
La traduzione è stata condotta sulla seguente edizione: Ludwig Wittgenstein, "Notes Dictated to G.E. Moore in Norway", in Notebooks 1914-1916, a cura di G. H. von Wright e G. E. M. Anscombe, Harper & Row, 1969, pp. 93-106. La traduzione è stata revisionata da Michele Lavazza, che ha anche curato la presente edizione digitale. Il testo originale è nel pubblico dominio nel suo paese di origine e in tutti i paesi dove i diritti di proprietà intellettuale scadono 70 anni o meno dopo la morte dell’autore. Questa traduzione è stata realizzata dal Ludwig Wittgenstein Project grazie al sostegno dell’Università degli Studi di Milano, erogato nell’ambito del bando 2021-2022 per il finanziamento delle attività culturali e sociali a cui il Ludwig Wittgenstein Project ha partecipato in collaborazione con l’Associazione Culturale La Taiga. È pubblicata secondo i termini della licenza Creative Commons Attribuzione – Condividi allo stesso modo 4.0.
Ludwig Wittgenstein
Note dettate a G.E. Moore in Norvegia
Le cosiddette “proposizioni” logiche mostrano [le] proprietà logiche del linguaggio e dunque dell’Universo, ma non dicono nulla.
Ciò significa che semplicemente osservandole puoi vedere questi legami veri e propri; invece, in una proposizione vera e propria, non puoi vedere che cos’è vero osservandola.
È impossibile dire che cosa sono queste proprietà, perché per farlo ti servirebbe un linguaggio sprovvisto di tali proprietà, ed è impossibile che questo sia un linguaggio vero e proprio. Impossibile costruire [un] linguaggio illogico.
Affinché tu possa disporre di un linguaggio in grado di esprimere o dire tutto ciò che può essere detto, il linguaggio in questione deve avere certe proprietà; e quando le cose stanno così, il fatto che il linguaggio possiede queste proprietà non può più essere detto in tale linguaggio né in qualsivoglia linguaggio.
Un linguaggio illogico sarebbe un linguaggio in cui, per esempio, tu potessi mettere un evento in un buco.
Quindi un linguaggio che può esprimere tutto rispecchia certe proprietà del mondo per mezzo di queste proprietà che deve avere; le cosiddette “proposizioni” logiche mostrano in modo sistematico tali proprietà.
Il modo in cui, solitamente, le proposizioni logiche mostrano tali proprietà è il seguente: diamo una certa descrizione di un tipo di simbolo; scopriamo che altri simboli, combinati in certe maniere, producono un simbolo di questa descrizione; e il fatto che lo facciano mostra qualcosa riguardo a questi simboli.
Di regola la descrizione [fornita] nella Logica ordinaria è la descrizione di una tautologia; ma altre descrizioni potrebbero mostrare altrettanto bene, per esempio, una contraddizione.
Ogni vera proposizione mostra qualcosa, oltre a ciò che dice, sull’Universo: poiché, se non ha senso, non può essere utilizzata; e se ha senso, rispecchia qualche proprietà logica dell’Universo.
Per esempio, prendi ϕa, ϕa ⊃ ψa, ψa. Semplicemente osservando queste tre proposizioni, posso vedere che la 3 segue dalla 1 e dalla 2; cioè posso vedere ciò che si chiama la verità di una proposizione logica, ossia della proposizione ϕa . ϕa ⊃ ψa : ⊃ : ψa. Ma questa non è una proposizione; vedendo però che si tratta di una tautologia posso vedere ciò che ho già visto osservando le tre proposizioni: la differenza è che adesso vedo che è una tautologia.
Vogliamo dire, per comprendere [quanto] sopra, quali proprietà deve avere un simbolo per essere una tautologia.
Ci sono molti possibili modi di dire ciò:
Un modo consiste nel fornire certi simboli; poi fornire un insieme di regole per combinarli; e poi dire: qualunque simbolo formato con questi simboli, combinati secondo una delle regole date, è una tautologia. Ciò ovviamente dice qualcosa sul tipo di simbolo che puoi ottenere in tale maniera.
Questa è effettivamente la procedura della vecchia Logica: ci fornisce delle cosiddette proposizioni primitive; delle cosiddette regole di deduzione; e poi dice che ciò che ottieni applicando le regole alle proposizioni è una proposizione logica che hai dimostrato. La verità è che essa ti dice qualcosa riguardo al tipo delle proposizioni che hai ottenuto, cioè che esso può essere derivato dai simboli iniziali per mezzo di queste regole di combinazione (= è una tautologia).
Le proposizioni logiche sono forme di dimostrazione: mostrano che una o più proposizioni seguono da una (o più).
Le proposizioni logiche mostrano qualcosa, perché il linguaggio in cui sono espresse può dire ogni cosa che può essere detta.
Questa stessa distinzione tra ciò che può essere mostrato dal linguaggio ma non detto spiega la difficoltà che si avverte a proposito dei tipi – per esempio, per quanto concerne [la] differenza tra cose, fatti, proprietà, relazioni. Che M è una cosa non può essere detto; è privo di senso: ma qualcosa è mostrato dal simbolo “M”. Allo stesso modo, il fatto che una proposizione è una proposizione soggetto-predicato non può essere detto: è però mostrato dal simbolo.
Dunque una teoria dei tipi è impossibile. Essa cerca di dire qualcosa sui tipi, mentre si può parlare soltanto dei simboli. Ma ciò che dici sui simboli non è che questo simbolo ha quel tipo, il che sarebbe privo di senso per [la] stessa ragione: dici invece semplicemente: questo è il simbolo, per prevenire un fraintendimento. Per esempio, in “a R b”, “R” non è un simbolo, ma il fatto che “R” sta tra un nome e un altro simbolizza. Qui non abbiamo detto: questo simbolo non è di questo tipo ma di quello, bensì soltanto: questo simbolizza e non quello. Anche tale locuzione sembra ripetere lo stesso errore, perché “simbolizza” è “tipicamente ambiguo”. La vera analisi è: “R” propriamente non è un nome e il fatto che “R” sta tra “a” e “b” esprime una relazione. Qui ci sono due proposizioni di tipo diverso connesse da “e”.
È ovvio che, per esempio, con una proposizione soggetto-predicato, sempre che essa abbia un qualche senso, ne vedi la forma non appena comprendi la proposizione, nonostante tu non sappia se è vera o falsa. Anche se ci fossero proposizioni della forma “M è una cosa”, esse sarebbero superflue (tautologiche) perché quello che ciò tenta di dire è qualcosa che vedi già quando vedi “M”.
Nell’espressione menzionata sopra “a R b”, parlavamo solo di questo “R” particolare, ma ciò che vogliamo fare è parlare di tutti i simboli simili. Dobbiamo dire: in qualunque simbolo di questa forma ciò che corrisponde a “R” propriamente non è un nome, e il fatto che [“R” sta tra “a” e “b”] esprime una relazione. Questo è ciò che si tentava di esprimere con l’espressione priva di senso: simboli come questo sono di un certo tipo. Questo non puoi dirlo, perché per dirlo devi prima sapere qual è il simbolo: e nel saperlo vedi [il] tipo e dunque anche [il] tipo di [ciò che è] simbolizzato. Ossia, nel sapere che cosa simbolizza, sai tutto ciò che c’è da sapere; non puoi dire nulla riguardo al simbolo.
Per esempio: considera le due proposizioni 1) “ciò che simbolizza qui è una cosa”, 2) “ciò che simbolizza qui è un fatto relazionale (= relazione)”. Queste proposizioni sono prive di senso per due ragioni: a) perché menzionano “cosa” e “relazione”; b) perché le menzionano in proposizioni della stessa forma. Le due proposizioni, se propriamente analizzate, devono essere espresse in forme interamente diverse; e non vi devono figurare né la parola “cosa” né la parola “relazione”.
Ora vedremo come analizzare correttamente le proposizioni in cui figurano “cosa”, “relazione”, etc.
1) Prendi ϕx. Vogliamo spiegare il significato di “in ‘ϕx’ una cosa simbolizza”. L’analisi è:
(∃y) . y simbolizza . y = “x” . “ϕx”
[“x” è il nome di y: “ϕx” = “‘ϕ’ è alla sinistra di ‘x’” e dice ϕx.]
N.B. “x” non può essere il nome di questo singolo frego y, perché questo non è una cosa: ma può essere il nome di una cosa; e dobbiamo comprendere che quel che stiamo facendo è spiegare ciò che si intenderebbe dicendo di un simbolo ideale, che effettivamente consisteva nel fatto che una cosa era a sinistra di un’altra, che in esso a simbolizzare era una cosa.
(N. B. Nell’espressione (∃y) . ϕy, si è inclini a dire che ciò significa “c’è una cosa tale per cui…”. Invece dovremmo dire “c’è una y, tale per cui…”; dove il fatto che la y simbolizza esprime ciò che intendiamo.)
In generale: quando tali proposizioni sono analizzate, mentre le parole “cosa”, “fatto”, etc. scompariranno, al loro posto apparirà un nuovo simbolo, della stessa forma di quello di cui stiamo parlando; e dunque sarà immediatamente ovvio che non possiamo ottenere l’un tipo di proposizione a partire dall’altro per sostituzione.
Nel nostro linguaggio i nomi non sono cose: non sappiamo cosa sono: sappiamo solo che sono di un tipo diverso rispetto alle relazioni, etc. etc. Il tipo di un simbolo di una relazione è in parte fissato da[l] tipo di [un] simbolo di [una] cosa, poiché un simbolo di [quest’]ultimo tipo deve presentarsi in esso.
N.B. In ogni proposizione ordinaria, per esempio “Moore buono”, questo mostra e non dice che “Moore” sta a sinistra di “buono;” e qui ciò che è mostrato può essere detto da un’altra proposizione. Ma ciò vale soltanto per quella parte di ciò che è mostrato che è arbitraria. Le proprietà logiche che la proposizione mostra non sono arbitrarie, e che essa le possiede non può essere detto in alcuna proposizione.
Quando diciamo di una proposizione della forma “a R b” che ciò che simbolizza è che “R” sta tra “a” e “b”, va ricordato che in effetti la proposizione è suscettibile di analisi ulteriore perché a, R e b non sono semplici. Ciò che però sembra certo è che alla fine, dopo averla analizzata, arriveremo a proposizioni della stessa forma dal punto di vista del fatto che esse consistono nello stare una cosa tra altre due cose.
Come possiamo parlare della forma generale di una proposizione, senza conoscere alcuna proposizione inanalizzabile in cui figurano nomi e relazioni particolari? Ciò che ci giustifica a farlo è il fatto che, pur non conoscendo alcuna proposizione inanalizzabile di questo tipo, possiamo comunque comprendere ciò che è inteso da una proposizione della forma (∃x, y, R) . x R y (la quale è inanalizzabile), anche se non conosciamo alcuna proposizione della forma x R y.
Se hai una proposizione inanalizzabile nella quale figurano nomi e relazioni particolari (e proposizione inanalizzabile = proposizione in cui figurano solo simboli fondamentali = simboli non suscettibili di definizione) allora da essa puoi sempre formare una proposizione della forma (∃x, y, R) . x R y, la quale, pur non contenendo nomi o relazioni particolari, è inanalizzabile.
2) Qui la questione può essere esplicata nel modo seguente. Prendi ϕa e ϕA: e chiediti che cosa si intende dicendo “c’è una cosa in ϕa e un complesso in ϕA”?
1) significa: (∃x) . ϕx . x = A
2) significa: (∃x, ψξ) . ϕA = ψx . ϕx.
Uso di proposizioni logiche. Puoi trovarne una così complicata da non accorgerti, osservandola, che è una tautologia; ma hai mostrato che può essere derivata con certe operazioni da certe altre proposizioni secondo la nostra regola per la costruzione delle tautologie; e dunque sei in grado di vedere che una cosa segue da un’altra, mentre altrimenti non saresti stato capace di vederlo. Per esempio, se la nostra tautologia è della forma p ⊃ q puoi vedere che q segue da p; e avanti così.
La Bedeutung di una proposizione è il fatto che le corrisponde; per esempio, se la nostra proposizione è “a R b”, se è vera, il fatto corrispondente sarebbe il fatto a R b, se è falsa, il fatto ~ a R b. Ma sia “il fatto a R b” sia “il fatto ~ a R b” sono simboli incompleti, che vanno analizzati.
Che una proposizione ha una relazione (in senso lato) con la Realtà diversa da quella di Bedeutung è mostrato dal fatto che puoi comprenderla quando non ne conosci la Bedeutung, cioè se non sai se è vera o falsa. Esprimiamolo dicendo “essa ha senso” (Sinn).
Analizzando la Bedeutung, arrivi al Sinn nel modo seguente:
Vogliamo spiegare la relazione delle proposizioni con la realtà.
La relazione è così: i suoi semplici hanno significato = sono nomi di semplici; e le sue relazioni hanno una relazione ben diversa con le relazioni; e questi due fatti già stabiliscono una specie di corrispondenza tra una proposizione che contiene questi e soltanto questi e la realtà: per esempio se tutti i semplici di una proposizione sono noti, sappiamo già che possiamo descrivere la realtà dicendo che si comporta in un certo modo nei confronti dell’intera proposizione. (Questo equivale al dire che possiamo confrontare la realtà con la proposizione. Nel caso di due linee possiamo confrontarle per quanto riguarda la loro lunghezza senza alcuna convenzione: il confronto è automatico. Ma nel nostro caso la possibilità del confronto dipende dalle convenzioni con cui abbiamo dato ai nostri semplici (nomi e relazioni) i loro significati.)
Resta soltanto da aggiustare il metodo di confronto dicendo che cosa nei nostri semplici deve dire che cosa della realtà. Supponiamo, per esempio, di prendere due linee di lunghezza diversa: e diciamo che il fatto che la più corta ha la lunghezza che ha deve significare che la più lunga ha la lunghezza che essa ha. Avremmo dovuto allora stabilire riguardo al significato della più corta una convenzione, del genere che adesso dobbiamo fornire.
Ne consegue che “vero” e “falso” non sono proprietà accidentali di una proposizione tali che, quando essa ha significato, possiamo dire che è anche vera o falsa: al contrario, che una proposizione ha significato significa che è vera o falsa: l’essere vera o falsa in effetti costituisce quella relazione della proposizione con la realtà alla quale ci riferiamo dicendo che la proposizione in questione ha significato (Sinn).
A prima vista sembra esserci una certa ambiguità in ciò che si intende dicendo che una proposizione è “vera”, per via del fatto che, a quanto sembra, nel caso di proposizioni diverse, il modo in cui esse corrispondono ai fatti a cui corrispondono è molto diverso. Ma ciò che è davvero comune a tutti i casi è che essi devono avere la forma generale di una proposizione. Nel fornire la forma generale di una proposizione spieghi quale tipo di modi di mettere assieme i simboli di cose e di relazioni corrisponderà (sarà analogo) al fatto che le cose abbiano tali relazioni nella realtà. Nel farlo dici ciò che si intende dicendo che una proposizione è vera; e devi farlo una volta per tutte. Dire “questa proposizione ha senso” significa “‘questa proposizione è vera’ significa…”. (“p” è vero = “p” . p . Def.: solo invece di “p” dobbiamo qui introdurre la forma generale di una proposizione).
A prima vista sembra che la notazione ab debba essere sbagliata, perché pare trattare il vero e il falso esattamente allo stesso livello. Dev’essere possibile vedere dai simboli stessi che c’è una differenza essenziale tra i poli, se la notazione dev’essere giusta; e pare che di fatto ciò sia impossibile.
L’interpretazione di un simbolismo non deve dipendere dal fatto di fornire una diversa interpretazione a simboli degli stessi tipi.
L’asimmetria viene introdotta fornendo una descrizione di una forma particolare di simbolo che chiamiamo una “tautologia”. La descrizione del simbolo ab, presa da sola, è simmetrica nei confronti di a e di b; ma questa descrizione più il fatto che ciò che soddisfa la descrizione di una tautologia è una tautologia è asimmetrico rispetto a essi. (Dire che una descrizione è simmetrica rispetto a due simboli significa che potremmo sostituirne uno con l’altro e che la descrizione rimarrebbe la stessa, ossia avrebbe lo stesso significato.)
Prendi p . q e q. Quando scrivi p . q nella notazione ab, è impossibile vedere soltanto dal simbolo che q ne consegue, perché se tu dovessi interpretare il polo del vero come quello del falso, lo stesso simbolo starebbe per p ∨ q, da cui q non consegue. Ma non appena dici quali simboli sono tautologie, tutt’a un tratto diventa possibile vedere, dal fatto che essi sono tautologie e dal simbolo originale, che q ne consegue.
Le proposizioni logiche, naturalmente, mostrano tutte qualcosa di diverso: tutte mostrano nello stesso modo, ossia per il fatto che sono tautologie, ma sono tautologie diverse e dunque mostrano ognuna qualcosa di diverso.
Ciò che non è arbitrario nei nostri simboli non sono i simboli stessi, né le regole che forniamo; ma il fatto che, avendo dato certe regole, altre sono fissate = seguono logicamente.
Quindi, anche se sarebbe possibile interpretare la forma che prendiamo per la forma di una tautologia come invece la forma di una contraddizione, e viceversa, esse sono diverse nella forma logica perché, nonostante la forma apparente dei simboli sia la stessa, ciò che in essi simbolizza è diverso, e dunque ciò che riguardo ai simboli consegue da un’interpretazione sarà diverso da ciò che consegue dall’altra. Ma la differenza tra a e b non è una differenza nella forma logica, cosicché da questa differenza soltanto non seguirà nulla per quanto riguarda l’interpretazione di altri simboli. Dunque, per esempio, i simboli p . q, p ∨ q sembrano avere esattamente la stessa forma logica nella notazione ab. Eppure, dicono qualcosa di completamente diverso; e, se ti chiedi perché, la risposta pare essere: in un caso il frego in cima ha la forma b, nell’altro caso ha la forma a. Mentre l’interpretazione di una tautologia come una tautologia è un’interpretazione di una forma logica, non l’elargizione di un significato a un frego dalla forma particolare. La cosa importante è che l’interpretazione della forma del simbolismo deve essere fissata fornendo un’interpretazione alle sue proprietà logiche, non fornendo interpretazioni a particolari freghi.
Le costanti logiche non possono essere trasformate in variabili: perché ciò che simbolizza in esse non è lo stesso; tutti i simboli a cui può essere sostituita una variabile simbolizzano allo stesso modo.
Descriviamo un simbolo e diciamo arbitrariamente “un simbolo così descritto è una tautologia”. E allora ne segue immediatamente sia che ogni altro simbolo rispondente alla stessa descrizione è una tautologia, sia che ogni simbolo che non vi corrisponde non lo è. Ossia, abbiamo arbitrariamente stabilito che ogni simbolo così descritto dev’essere una tautologia; e, una volta stabilito questo, per quanto riguarda qualunque altro simbolo non è più arbitrario se sia una tautologia oppure no.
Avendo così stabilito cos’è una tautologia e cosa non lo è, possiamo allora, avendo stabilito di nuovo arbitrariamente che la relazione a-b è transitiva, ricavare dall’insieme di questi due fatti che “p ≡ ~(~p)” è una tautologia. Perché ~(~p) = a-b-a-p-b-a-b. Il punto è: il processo di ragionamento con cui arriviamo al risultato che a-b-a-p-b-a-b è lo stesso simbolo che a-p-b è esattamente identico a quello per mezzo del quale scopriamo che il suo significato è lo stesso, ossia quello in cui ragioniamo che se b-a-p-b-a, allora non a-p-b, se a-b-a-p-b-a-b allora non b-a-p-b-a, e perciò se a-b-a-p-b-a-b, allora a-p-b.
Dal fatto che a-b è transitivo segue che dove abbiamo a-b-a la prima a intrattiene con la seconda a la stessa relazione che intrattiene con b. Proprio come dal fatto che a-vero implica b-falso, e che b-falso implica c-vero, ricaviamo che a-vero implica c-vero. E saremo in grado di vedere, avendo stabilito la descrizione di una tautologia, che p ≡ ~(~p) è una tautologia.
Il fatto che, quando viene fornita una certa regola, un simbolo è tautologico mostra una verità logica.
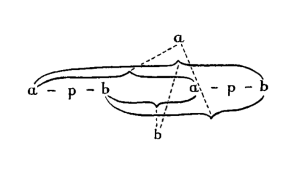
Questo simbolo potrebbe essere interpretato sia come una tautologia sia come una contraddizione.[1]
Nello stabilire che ciò va interpretato come una tautologia e non come una contraddizione, non sto assegnando un significato ad a e a b; ovverosia non sto dicendo che essi simbolizzano cose diverse ma nello stesso modo. Sto dicendo invece che il modo in cui il polo a è connesso con l’intero simbolo simbolizza in un modo diverso dal modo in cui simbolizzerebbe se il simbolo venisse interpretato come una contraddizione. E aggiungo i freghi a e b solo per mostrare in quali modi la connessione sta simbolizzando, affinché risulti evidente che ogniqualvolta lo stesso frego figura nella posizione corrispondente in un altro simbolo, anche in quel caso la connessione sta simbolizzando nello stesso modo.
Potremmo, naturalmente, simbolizzare ogni funzione ab senza utilizzare affatto due poli esterni, semplicemente, per esempio, omettendo il polo b; e qui a simbolizzare sarebbe il fatto che le tre coppie di poli interni delle proposizioni siano connessi in un certo modo con il polo a e che l’altra coppia non vi sia connessa. E quindi la differenza tra i freghi a e b, dove li utilizziamo, mostra soltanto che è un diverso stato di cose che sta simbolizzando in un caso e nell’altro: in un caso il fatto che certi poli interni sono connessi in un certo modo con un polo esterno, nell’altro caso il fatto che non lo sono.
Il simbolo per una tautologia, in qualunque forma lo mettiamo, sia che omettiamo il polo a sia che omettiamo il polo b, è sempre passibile di venire impiegato come il simbolo di una contraddizione; soltanto non nello stesso linguaggio.
La ragione per cui ~x è privo di significato è semplicemente che non abbiamo dato alcun significato al simbolo ~ξ. Cioè, sebbene ϕx e ϕp diano l’impressione di essere dello stesso tipo, non lo sono, perché per poter fornire un significato a ~x dovresti avere una qualche proprietà ~ξ. Ciò che simbolizza in ϕξ è che ϕ sta a sinistra di un nome vero e proprio e ovviamente ciò non si verifica in ~p. Ciò che è comune a tutte le proposizioni in cui figura il nome di una proprietà (per parlare approssimativamente) è il fatto che tale nome sta a sinistra di una forma-nome.
La ragione per cui, per esempio, sembra che “Platone Socrate” possa avere un significato, mentre non si sospetterà mai che “Abracadabra Socrate” ne abbia uno, consiste nel fatto che sappiamo che “Platone” ha un significato e non osserviamo che, affinché l’intera espressione abbia un significato, ciò che è necessario non è che “Platone” abbia un significato, ma che ce l’abbia il fatto che “Platone” sta a sinistra di un nome.
La ragione per cui “la proprietà di non essere verde non è verde” è privo di senso consiste nel fatto che abbiamo fornito un significato soltanto al fatto che “verde” sta a destra di un nome; e “la proprietà di non essere verde” ovviamente non è un nome.
ϕ non potrà mai stare a sinistra del simbolo di una proprietà (o in qualsiasi altra relazione con esso). Perché il simbolo di una proprietà, per esempio ψx, è che ψ sta alla sinistra di una forma-nome, e un altro simbolo ϕ non potrà mai stare a sinistra di un tale fatto: se potesse, disporremmo di un linguaggio illogico, il che è impossibile.
p è falso = ~(p è vero) Def.
È molto importante che le relazioni logiche apparenti ∨, ⊃, etc. necessitino di parentesi, punti, etc., ovverosia che abbiano “raggi d’azione”; ciò basta a mostrare che esse non sono relazioni. Questo fatto è stato trascurato proprio per la sua universalità – che è proprio ciò che lo rende tanto importante.
Ci sono relazioni interne tra una proposizione e un’altra; ma una proposizione non può avere con un’altra la relazione interna che un nome ha con la proposizione di cui è un costituente, e che dovrebbe essere intesa dicendo che esso “figura” in essa. In questo senso una proposizione non può “figurare” in un’altra.
Le relazioni interne sono relazioni tra tipi che non possono essere espresse in proposizioni, ma sono tutte mostrate nei simboli stessi, e possono essere esibite sistematicamente in tautologie. Il motivo per cui giungiamo a chiamarle “relazioni” consiste nel fatto che le proposizioni logiche hanno con esse una relazione analoga a quelle che proposizioni propriamente relazionali hanno con le relazioni.
Le proposizioni possono avere l’una con l’altra molte relazioni interne diverse. Quella che ci autorizza a dedurne una dall’altra è che se, diciamo, ci sono ϕa e ϕa ⊃ ψa, allora ϕa . ϕa ⊃ ψa : ⊃ : ψa è una tautologia.
Il simbolo d’identità esprime la relazione interna tra una funzione e il suo argomento: per esempio, ϕa = (∃x) . ϕx . x = a.
È possibile vedere che la proposizione (∃x) . ϕx . x = a : ≡ : ϕa è una tautologia se si esprimono le condizioni della verità di (∃x) . ϕx . x = a, in successione, per esempio dicendo: ciò è vero se questo e questo; e ciò a suo volta è vero se questo e questo, etc., per (∃x) . ϕx . x = a; e poi anche per ϕa. Esprimere la questione in tal modo comporta di per sé una notazione gravosa, di cui la notazione ab è una traduzione più elegante.
Ciò che simbolizza in un simbolo è ciò che è comune a tutti i simboli con cui, in accordo con le regole della logica = regole sintattiche per la manipolazione dei simboli, lo si potrebbe sostituire.
La domanda se una proposizione ha senso (Sinn) non può mai dipendere dalla verità di un’altra proposizione che verte su un costituente della prima. Per esempio, la domanda se (x) x = x ha significato (Sinn) non può dipendere dalla domanda se (∃x) x = x è vera. Non descrive affatto la realtà, e ha a che fare quindi soltanto con simboli; e dice che essi devono simbolizzare, ma non che cosa simbolizzano.
È ovvio che i punti e le parentesi sono simboli, ed è ovvio che non hanno alcun significato indipendente. Per introdurre le cosiddette “costanti logiche” nella maniera corretta, devi dunque introdurre la nozione generale di tutte le loro possibili combinazioni = la forma generale di una proposizione. Introduci dunque sia le funzioni ab, sia l’identità, sia l’universalità (le tre costanti fondamentali) contemporaneamente.
La proposizione variabile p ⊃ p non è identica alla proposizione variabile ~(p . ~p). Gli universali corrispondenti sarebbero identici. La proposizione variabile ~(p . ~p) mostra che da ~(p . q) ottieni una tautologia sostituendo ~p a q, mentre l’altra non lo mostra.
È molto importante rendersi conto che il fatto di avere due relazioni diverse (a,b)R, (c,d)S non stabilisce una correlazione tra a e c, e b e d, oppure tra a e d, e b e c: non viene stabilita proprio nessuna correlazione. Naturalmente, nel caso di due coppie di termini uniti dalla stessa relazione, una correlazione c’è. Questo mostra che la teoria secondo cui un fatto relazionale conterrebbe i termini e le relazioni uniti da una copula (ε2) non è vera; se fosse vera, infatti, dovrebbe esserci una corrispondenza tra i termini di diverse relazioni.
Sorge la domanda: come può una proposizione (o funzione) figurare in un’altra proposizione? La proposizione o funzione stessa non potrà mai stare in relazione con gli altri simboli. Perciò dobbiamo introdurre immediatamente funzioni e nomi nella nostra forma generale di una proposizione; spiegando cosa si intende dando significato al fatto che i nomi stanno tra i |, e che la funzione sta a sinistra dei nomi.
È vero, in un certo senso, che le proposizioni logiche sono “postulati” – qualcosa che “richiediamo”; perché richiediamo una notazione soddisfacente.
Una tautologia (non una proposizione logica) non è priva di senso nella stessa maniera in cui, per esempio, lo è una proposizione in cui figurano parole che non hanno significato. Ciò che accade nella tautologia è che tutte le sue parti semplici hanno significato, ma le loro connessioni si paralizzano o distruggono a vicenda, in modo tale che risultano tutte connesse soltanto in maniera irrilevante.
Le funzioni logiche si presuppongono tutte a vicenda. Proprio come possiamo vedere che ~p non ha senso, se neanche p ce l’ha; così possiamo anche dire che p non ha senso se non ha senso ~p. La questione è ben diversa con ϕa e a; poiché qui a ha un significato indipendente da ϕa, anche se ϕa lo presuppone.
Le costanti logiche sembrano essere simboli-complessi, ma d’altro canto sono reciprocamente intercambiabili. Dunque non sono davvero complessi; ciò che simbolizza è semplicemente il modo generale in cui sono combinate.
La combinazione di simboli in una tautologia non potrà mai corrispondere ad alcuna particolare combinazione dei loro significati – corrisponde a ogni possibile combinazione; e dunque ciò che simbolizza non può essere la connessione dei simboli.
Dal fatto che vedo che un punto è a sinistra di un altro, o che un colore è più scuro di un altro, pare conseguire che è così; e in tal caso, ciò può essere soltanto perché tra le due cose c’è una relazione interna; e potremmo esprimerlo dicendo che la forma del secondo è parte della forma del primo. Potremmo così dare un senso all’asserzione secondo cui le leggi logiche sono forme del pensiero e spazio e tempo forme dell’intuizione.
Diversi tipi logici possono non avere assolutamente nulla in comune. Ma il mero fatto che si possa parlare della possibilità di una relazione di n posizioni, o di un’analogia tra una relazione con due posizioni e una relazione con quattro posizioni, mostra che relazioni con posizioni in numero diverso hanno qualcosa in comune, che dunque non si tratta qui di una differenza di tipo, ma di una differenza come quella tra nomi diversi – qualcosa che dipende dall’esperienza. Ciò risponde alla domanda su come possiamo sapere di essere davvero arrivati alla forma più generale di una proposizione. Dobbiamo solo introdurre ciò che è comune a tutte le relazioni con posizioni in numero qualsiasi.
La relazione tra “io credo p” e “p” può essere confrontata con la relazione tra “‘p’ dice (besagt) p” e p: il fatto che io sia un semplice è tanto impossibile quanto il fatto che lo sia “p”.
- ↑ Nota del curatore dell’edizione Ludwig Wittgenstein Project: Il diagramma disegnato origariamente da Moore aveva questo aspetto:
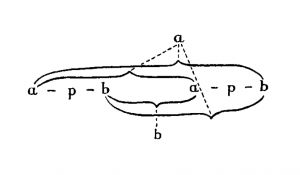
L’equivalente di questo simbolo nella notazione odierna delle tavole di verità (nella quale le combinazioni tra i valori di verità possibili delle singole proposizioni sono mostrate tramite una tabella e per indicare i due poli vengono utilizzati “V” e “F” anziché rispettivamente “a” e “b”) è il seguente:
p p p ≡ ~(~p) V V V V F V F V F F F V Tale diagramma, tuttavia, non corrisponde alle condizioni di verità della proposizione p ≡ ~(~p), che nella notazione odierna sono le seguenti:
p p p ≡ ~(~p) V V V V F F F V F F F V L’edizione cartacea sulla quale è stata condotta questa traduzione riproduce fedelmente il disegno originale di Moore. Nella presente edizione digitale, il diagramma originale scorretto è stato invece sostituito da una versione che corrisponde a quest’ultima tavola di verità.
Per maggiori dettagli si veda Michael A.R. Biggs, “Editing Wittgenstein’s Notes on Logic. Vol. 1”, Working Papers from the Wittgenstein Archives at the University of Bergen, n. 11, 1996, § 1.8.
This translation was made possible by the financial support of: