Zettel: Difference between revisions
No edit summary |
No edit summary |
||
| Line 6: | Line 6: | ||
{{colophon | {{colophon | ||
|translator = Herausgegeben von [https://en.wikipedia.org/wiki/G._E._M._Anscombe G. E. M. Anscombe] und [https://en.wikipedia.org/wiki/Georg_Henrik_von_Wright G. H. von Wright] | |translator = Herausgegeben von [https://en.wikipedia.org/wiki/G._E._M._Anscombe G. E. M. Anscombe] und [https://en.wikipedia.org/wiki/Georg_Henrik_von_Wright G. H. von Wright] | ||
|notes= Diese digitale Ausgabe ist | |notes= Diese digitale Ausgabe ist eine Reproduktion von L. Wittgenstein, ''Zettel''. Herausgegeben von G. E. M. Anscombe und G. H. von Wright. Basil Blackwell, Oxford 1967. | ||
}} | }} | ||
| Line 771: | Line 771: | ||
{{ParZ|248}} (Etwas, was auf den ersten Blick ausschaut wie ein Satz und keiner ist.) Der folgende Vorschlag zur Konstruktion einer Straßenwalze wurde mir einmal mitgeteilt. Der Motor befindet sich im Innern der hohlen Walze. Die Kurbelwelle läuft durch die Mitte der Walze und ist an beiden Enden durch Speichen mit dem Walzenrand verbunden. Der Zylinder des Motors ist an der Innenseite der Walze befestigt. Auf den ersten Blick sieht diese Konstruktion wie eine Maschine aus. Aber sie ist ein starres System, und der Kolben kann sich im Zylinder nicht aus und ein bewegen. Wir haben ihn der Bewegungsmöglichkeit beraubt und wissen es nicht. | {{ParZ|248}} (Etwas, was auf den ersten Blick ausschaut wie ein Satz und keiner ist.) Der folgende Vorschlag zur Konstruktion einer Straßenwalze wurde mir einmal mitgeteilt. Der Motor befindet sich im Innern der hohlen Walze. Die Kurbelwelle läuft durch die Mitte der Walze und ist an beiden Enden durch Speichen mit dem Walzenrand verbunden. Der Zylinder des Motors ist an der Innenseite der Walze befestigt. Auf den ersten Blick sieht diese Konstruktion wie eine Maschine aus. Aber sie ist ein starres System, und der Kolben kann sich im Zylinder nicht aus und ein bewegen. Wir haben ihn der Bewegungsmöglichkeit beraubt und wissen es nicht. | ||
{{ParZ|249}} "Nichts leichter, als sich einen 4-dimensionalen Würfel vorstellen! Er schaut so aus:<ref>Im Original findet man keine Zeichnung: der Leser möge sich etwas Passendes | {{ParZ|249}} "Nichts leichter, als sich einen 4-dimensionalen Würfel vorstellen! Er schaut so aus:<ref>Im Original findet man keine Zeichnung: der Leser möge sich etwas Passendes ausdenken. Es gibt verschiedene Möglichkeiten; wir haben eine Zeichnung von <span class=plainlinks>[https://commons.wikimedia.org/wiki/User:A2569875 A2569875]</span> (<span class=plainlinks>[https://creativecommons.org/licenses/by-sa/3.0/deed.en CC BY-SA]</span>) benutzt. Herausgeber der digitalen Ausgabe.</ref> | ||
[[File:Zettel 249.gif|center|link=https://commons.wikimedia.org/wiki/File:Net_of_tesseract.gif|class=comfy]] | [[File:Zettel 249.gif|center|link=https://commons.wikimedia.org/wiki/File:Net_of_tesseract.gif|class=comfy]] | ||
| Line 845: | Line 845: | ||
{{ParZ|271}} Wozu dient ein Satz wie dieser: "Wir können uns die Empfindungen eines Jongleurs wie Rastelli gar nicht vorstellen"? | {{ParZ|271}} Wozu dient ein Satz wie dieser: "Wir können uns die Empfindungen eines Jongleurs wie Rastelli gar nicht vorstellen"? | ||
{{ParZ|272}} "Es hat Sinn, von einer endlosen Baumreihe zu reden; ich kann mir doch vorstellen, daß eine Baumreihe ohne Ende weiterläuft." D. h. etwa: Wenn es Sinn hat zu sagen, die Baumreihe komme hier zu einem Ende, hat es Sinn zu sagen, [sie komme nie zu einem Ende].<ref>Vermutung der Herausgeber.</ref> Ramsey pflegte auf solche Fragen zu antworten: es sei ''eben doch'' möglich, so etwas zu denken. So etwa, wie man sagt "Die Technik leistet heute eben Dinge, die du dir gar nie vorstellen kannst."——Nun, da muß man herausfinden, was du dabei denkst. (Daß du versicherst, diese Phrase ließe sich ''denken''—was kann ich damit machen? Darauf kommt es ja nicht an. Ihr Zweck ist ja nicht der, Nebel in deiner Seele aufsteigen zu lassen.) ''Was'' du meinst—Wie ist es herauszufinden? Wir müssen geduldig prüfen, wie dieser Satz angewandt werden soll. Wie ''rund um ihn'' alles aussieht. Da wird sich sein Sinn zeigen. | {{ParZ|272}} "Es hat Sinn, von einer endlosen Baumreihe zu reden; ich kann mir doch vorstellen, daß eine Baumreihe ohne Ende weiterläuft." D. h. etwa: Wenn es Sinn hat zu sagen, die Baumreihe komme hier zu einem Ende, hat es Sinn zu sagen, [sie komme nie zu einem Ende].<ref>Vermutung der Herausgeber der Papierausgabe.</ref> Ramsey pflegte auf solche Fragen zu antworten: es sei ''eben doch'' möglich, so etwas zu denken. So etwa, wie man sagt "Die Technik leistet heute eben Dinge, die du dir gar nie vorstellen kannst."——Nun, da muß man herausfinden, was du dabei denkst. (Daß du versicherst, diese Phrase ließe sich ''denken''—was kann ich damit machen? Darauf kommt es ja nicht an. Ihr Zweck ist ja nicht der, Nebel in deiner Seele aufsteigen zu lassen.) ''Was'' du meinst—Wie ist es herauszufinden? Wir müssen geduldig prüfen, wie dieser Satz angewandt werden soll. Wie ''rund um ihn'' alles aussieht. Da wird sich sein Sinn zeigen. | ||
{{ParZ|273}} Hardy: "That 'the finite cannot understand the infinite' should surely be a theological and not a mathematical war-cry." Es ist wahr, dieser Ausdruck ist ungeschickt. Aber was Leute damit sagen wollen, ist: "Es muß hier doch mit rechten Dingen zugehen! Woher dieser Sprung von Endlichen zum Unendlichen?" Und so ganz unsinnig ist die Ausdrucksweise auch nicht—nur ist das 'Endliche', was das Unendliche nicht soll denken können, nicht der Mensch', oder 'unser Verstand', sondern der Kalkül. Und ''wie'' dieser das 'Unendliche' denkt, dies ist wohl einer Untersuchung wert. Und die ist zu vergleichen der genauen Untersuchung und Klärung der Geschäftsgebarung eines Unternehmens durch einen Chartered Accountant. Das Ziel ist eine übersichtliche, vergleichende Darstellung aller Anwendungen, Illustrationen, Auffassungen des Kalküls. Die vollkommene Übersicht über alles, was Unklarheit schaffen kann. Und diese Übersicht muß sich auf ein weites Gebiet erstrecken, denn die Wurzeln unserer Ideen reichen weit.—"Das Endliche kann nicht das Unendliche verstehen", heißt hier: ''So'' kann es nicht zugehen, wie ihr es in charakteristischer Oberflächlichkeit darstellt. | {{ParZ|273}} Hardy: "That 'the finite cannot understand the infinite' should surely be a theological and not a mathematical war-cry." Es ist wahr, dieser Ausdruck ist ungeschickt. Aber was Leute damit sagen wollen, ist: "Es muß hier doch mit rechten Dingen zugehen! Woher dieser Sprung von Endlichen zum Unendlichen?" Und so ganz unsinnig ist die Ausdrucksweise auch nicht—nur ist das 'Endliche', was das Unendliche nicht soll denken können, nicht der Mensch', oder 'unser Verstand', sondern der Kalkül. Und ''wie'' dieser das 'Unendliche' denkt, dies ist wohl einer Untersuchung wert. Und die ist zu vergleichen der genauen Untersuchung und Klärung der Geschäftsgebarung eines Unternehmens durch einen Chartered Accountant. Das Ziel ist eine übersichtliche, vergleichende Darstellung aller Anwendungen, Illustrationen, Auffassungen des Kalküls. Die vollkommene Übersicht über alles, was Unklarheit schaffen kann. Und diese Übersicht muß sich auf ein weites Gebiet erstrecken, denn die Wurzeln unserer Ideen reichen weit.—"Das Endliche kann nicht das Unendliche verstehen", heißt hier: ''So'' kann es nicht zugehen, wie ihr es in charakteristischer Oberflächlichkeit darstellt. | ||
Revision as of 14:29, 4 April 2021
Ludwig Wittgenstein
Zettel
Herausgegeben von G. E. M. Anscombe und G. H. von Wright
Diese digitale Ausgabe ist eine Reproduktion von L. Wittgenstein, Zettel. Herausgegeben von G. E. M. Anscombe und G. H. von Wright. Basil Blackwell, Oxford 1967.
Ludwig Wittgenstein
Zettel
1. W. James: der Gedanke sei schon am Anfang des Satzes fertig. Wie kann man das wissen?—Aber die Absicht, ihn auszusprechen, kann schon bestehen, ehe das erste Wort gesagt ist. Denn fragt man Einen "weißt du, was du sagen willst?", so wird er es oft bejahen.
2. Ich sage Einem "ich werde dir jetzt das Thema .... vorpfeifen", ich habe die Absicht, es zu pfeifen, und ich weiß schon, was ich pfeifen werde.
Ich habe die Absicht, dieses Thema zu pfeifen: habe ich es damit in irgendeinem Sinne etwa in Gedanken schon gepfiffen?
3. "Ich sage das nicht nur, ich meine etwas damit."—Soll man darauf fragen "Was?"——Dann kommt wieder ein Satz zur Antwort.—Oder kann man nicht so fragen, da der Satz etwa sagte "Ich sage das nicht nur, sondern es bewegt mich auch."
4. (Eine der irreführendsten Redeweisen ist die Frage "Was meine ich damit?"—Man könnte in den meisten Fällen darauf antworten "Gar nichts—ich sage ....".)
5. Kann ich denn nicht mit Worten meinen, was ich will?——Schau auf die Tür deines Zimmers, sage dabei eine Reihe beliebiger Laute, und meine damit eine Beschreibung dieser Tür!
6. "Sag 'a b c d' und meine damit: Das Wetter ist schön."—Soll ich also sagen, daß das Aussprechen eines Satzes einer uns geläufigen Sprache ein ganz anderes Erlebnis ist, als das Aussprechen von Lauten, die uns nicht als Satz geläufig sind? Wenn ich also die Sprache erlernte, in welcher "abcd" jenen Sinn haben,—würde ich nach und nach das uns bekannte Erlebnis beim Aussprechen dieser Buchstaben kriegen? Ja und nein.—Eine Hauptverschiedenheit der beiden Fälle liegt darin, daß ich mich im ersten nicht bewegen kann. Es ist da, als wäre eines meiner Gelenke in Schienen und ich noch nicht an sie gewöhnt und hätte die möglichen Bewegungen noch nicht inne, stieße also sozusagen in einemfort an.
7. Wenn ich zwei Freunde gleichen Namens habe, und ich schreibe einem von ihnen einen Brief; worin liegt es, daß ich ihn nicht dem andern schreibe? Am Inhalt? Aber der könnte für beide passen. (Die Adresse habe ich noch nicht geschrieben.) Nun, die Verbindung kann in der Vorgeschichte liegen. Dann aber auch in dem, was dem Schreiben folgt. Wenn mich nun jemand fragt "An welchen der beiden schreibst du?" und ich antworte ihm, schließe ich die Antwort aus der Vorgeschichte? Gebe ich sie nicht beinahe, wie ich sage "Ich habe Zahnschmerzen"?—Könnte ich im Zweifel darüber sein, welchem von beiden ich schreibe? Und wie sieht so ein Zweifelsfall aus?—Ja, wäre nicht auch der Fall einer Täuschung möglich: ich glaube dem Einen zu schreiben und schreibe dem Andern? Und wie sähe der Fall einer solchen Täuschung aus?
8. (Man sagt manchmal: "Was wollte ich nur in dieser Lade suchen?—Ach ja, die Photographie!" Und wenn uns dies einfällt, erinnern wir uns wieder an den Zusammenhang unsrer Handlung mit dem, was vorherging. Es könnte aber auch den · Fall geben: Ich öffne die Lade und krame in ihr; endlich komme ich gleichsam zur Besinnung und frage mich "Warum suche ich in dieser Lade herum?" Und dann kommt die Antwort "Ich will die Photographie des .... sehen". "Ich will", nicht "Ich wollte". Das Öffnen der Lade etc. geschah sozusagen automatisch und erhielt nachträglich eine Interpretation.)
9. "Ich wollte mit dieser Bemerkung ihn treffen." Wenn ich das höre, so kann ich mir dazu eine Situation und ihre Geschichte vorstellen. Ich könnte sie auf dem Theater darstellen, mich in den Seelenzustand versetzen, in dem ich ihn treffen will.—Aber wie ist dieser Seelenzustand zu beschreiben? also zu identifizieren?—Ich denke mich in die Situation hinein, nehme eine gewisse Miene und Stimme an etc. Was verbindet meine Worte mit ihm? Die Situation und meine Gedanken. Und meine Gedanken nicht anders als Worte, die ich ausspreche.
10. Angenommen, ich wollte auf einmal alle Wörter meiner Sprache durch andere ersetzen; wie könnte ich wissen, an welcher Stelle eines der neuen Wörter steht? Sind es die Vorstellungen, die die Plätze der Wörter halten?
11. Ich bin geneigt zu sagen: Ich 'zeige' in verschiedenen Sinne auf diesen Körper, auf seine Gestalt, auf seine Farbe etc.—Was heißt das?
Was heißt es: Ich 'höre' in anderem Sinne: das Klavier, seinen Klang, das Musikstück, den Klavierspieler, seine Geläufigkeit? Ich 'heirate' in einem Sinne eine Frau, in einem andern ihr Geld.
12. Das Meinen stellt man sich hier als eine Art geistiges Zeigen, Hinweisen vor.
13. In manchen spiritistischen Handlungen ist es wesentlich, daß man an eine bestimmte Person denke. Und wir haben hier den Eindruck, also wäre 'an ihn denken' gleichsam, ihn mit meinen Gedanken aufspießen. Oder es ist, als stäche ich immer wieder mit den Gedanken nach ihm hin. Denn sie schweifen etwa immer wieder ein wenig von ihm ab.
14. "Ich mußte plötzlich an ihn denken." Sein Bild schwebte mir etwa plötzlich vor. Wußte ich, daß es sein, des N. Bild war? Ich sagte es mir nicht. Worin lag es also, daß es das seine war? Vielleicht in dem, was ich später sagte oder tat.
15. Wenn Max sagt "Der Fürst trägt Vatersorge für die Truppen", so meint er Wallenstein.—Angenommen, jemand sagte: Wir wissen nicht, ob er Wallenstein meint; er könne in diesem Satz auch einen andern Fürsten meinen.
16. "Daß du das Klavierspiel meintest, bestand darin, daß du ans Klavierspiel dachtest."
"Daß du in diesem Brief diesen Menschen mit dem Wort 'du' meintest, bestand darin, daß du an ihn schriebst."
Der Irrtum ist zu sagen, Meinen bestehe in etwas.
17. "Als ich das sagte, wollte ich ihm nur einen Wink geben."—Wie kann ich wissen, daß ich es nur sagte, um ihm einen Wink zu geben? Nun, die Worte "Als ich es sagte etc." beschreiben eine bestimmte uns verständliche Situation. Wie schaut die Situation aus? Um sie zu beschreiben, muß ich einen Zusammenhang beschreiben.
18. Wie tritt er in diese Vorgänge ein:
- ich stach nach ihm,
- ich sprach zu ihm,
- ich rief ihn,
- ich sprach von ihm,
- ich stellte mir ihn vor,
- ich achte ihn?
19. Es ist falsch zu sagen: Ich meinte ihn, indem ich auf ihn sah. "Meinen" bezeichnet nicht: eine Tätigkeit, die ganz oder teilweise in den 'Äußerungen' des Meinens besteht.
20. Es wäre daher dumm, Meinen eine 'geistige Tätigkeit' zu nennen. Weil man damit eine falsche Vorstellung von der Funktion des Wortes begünstigt.
21. Ich sage "Komm her!" und zeige in der Richtung des A. B, der neben ihm steht, macht einen Schritt auf mich zu. Ich sage: "Nein; A soll kommen." Wird man das nun als eine Mitteilung über meine Seelenvorgänge auffassen? Gewiß nicht.—Und könnte man nicht doch daraus Schlüsse auf Vorgänge ziehen, die in mir beim Aussprechen des Befehls "Komm her!" stattgefunden haben?
Aber auf was für Vorgänge? Könnte man nicht mutmaßen, ich habe bei meinem Befehl auf A geschaut; mein Gedankengang habe mich zu ihm geleitet? Aber vielleicht kenne ich den B überhaupt nicht, stehe nur mit A in Verbindung. Dann hätte also, wer meine seelischen Vorgänge mutmaßte, ganz irregehen können, und hätte dennoch verstanden, daß ich den A und nicht den B gemeint habe.
22. Ich zeige mit der Hand und sage "Komm her!". A fragt "Hast du mich gemeint?" Ich sage "Nein; den B."—Was ging da vor, als ich den B meinte (da doch mein Zeigen es zweifelhaft ließ, welchen ich meinte)?—Ich sagte diese Worte, machte diese Handbewegung. Mußte noch mehr vorgehen, daß das Sprachspiel vor sich gehen konnte? Aber wußte ich nicht schon während des Zeigens, wen ich meinte? Wußte? Freilich,—nach den gewöhnlichen Kriterien des Wissens.
23. "Ich wollte in meiner Erklärung auf .... lossteuern." Mir schwebte dieses Ziel vor. Ich sah im Geist die Stelle des Buchs, auf die ich hinzielte.
Die Absicht beschreiben, heißt, was vorging, unter einem bestimmten Gesichtspunkte, für einen bestimmten Zweck beschreiben. Ich male ein bestimmtes Porträt der Vorgänge.
24. Statt "Ich habe ihn gemeint" kann man auch sagen "Ich habe von ihm gesprochen". Und wie macht man das: mit diesen Worten von ihm sprechen? Warum klingt es falsch, zu sagen "ich habe von ihm gesprochen, indem ich bei diesen Worten auf ihn zeigte"?
"Ihn meinen" heißt etwa: von ihm reden. Nicht: auf ihn zeigen. Und wenn ich von ihm rede, besteht freilich eine Verbindung zwischen meiner Rede und ihm, aber diese Verbindung liegt in der Anwendung der Rede, nicht in einem Akt des Zeigens. Das Zeigen ist selbst nur ein Zeichen, und es kann im Sprachspiel die Anwendung der Sätze regeln, also, was gemeint ist, anzeigen.
25. Wenn ich sage "Ich habe in diesem Zimmer einen Sessel gesehen", so kann ich mich meistens nur sehr beiläufig an das besondere Gesichtsbild erinnern, und es hat in den meisten Fällen auch gar keine Bedeutung. Der Gebrauch, der von dem Satz gemacht wird, geht an dieser Besonderheit vorbei. Ist es nun so auch, wenn ich sage "Ich habe den N gemeint"? Geht dieser Satz in der gleichen Weise an den Besonderheiten des Vorgangs vorbei?
26. Wenn ich mit einer Bemerkung auf N anspiele, so mag sich dies—wenn bestimmte Umstände gegeben sind—aus meinem Blick, Gesichtsausdruck, etc. ersehen lassen.
Daß du den Ausdruck "auf N anspielen" verstehst, kannst du dadurch zeigen, daß du Beispiele des Anspielens beschreibst. Was wirst du nun alles beschreiben? Vor allem Umstände. Dann was Einer sagt. Etwa auch seinen Blick etc. Dann, was der Anspielende tun will.
Und teile ich jemand dazu noch meine Gefühle, Vorstellungen etc., während ich diese Bemerkung machte (während dieser Anspielung), mit, so mögen diese das typische Bild des Anspielens (oder ein solches Bild) vervollständigen. Aber daraus folgt nicht, daß der Ausdruck "auf N anspielen" bedeute: sich so benehmen, dies fühlen, sich dies vorstellen, etc. Und hier wird mancher sagen: "Freilich nicht! das haben wir immer schon gesehen. Und es muß sich eben ein roter Faden durch alle diese Erscheinungen ziehen. Er ist mit ihnen sozusagen umsponnen, und daher schwer auffindbar."—Und das ist auch nicht wahr.
Aber es wäre auch falsch zu sagen, "anspielen" bezeichne eine Familie von geistigen und anderen Vorgängen.—Denn man kann zwar fragen "Welches war deine Anspielung auf N?", "Wie hast du den andern zu verstehen gegeben, daß du N meintest?"; aber nicht: "Wie hast du diese Äußerung als Anspielung auf N gemeint?"
"Ich habe in meiner Rede auf ihn angespielt."—"mit welchen Worten?"—"Ich habe auf ihn angespielt, als ich von einem Mann redete, der ....".
"Ich habe auf ihn angespielt", heißt ungefähr: Ich wollte, daß jemand bei diesen Worten an ihn denken solle. Aber "Ich wollte" ist nicht die Beschreibung eines Seelenzustandes, und "verstehen, daß N gemeint war" ist dies auch nicht.
27. Wenn die Situation zweideutig ist, ist es dann zweifelhaft, ob ich ihn meine? Bei meiner Aussage, ich habe ihn oder habe ihn nicht gemeint, urteile ich nicht nach der Situation. Und wenn ich nun nicht nach der Situation urteile, wonach urteile ich? Scheinbar nach gar nichts. Denn ich erinnere mich wohl an die Situation, aber deute sie. Ich kann z. B. meinen Seitenblick auf ihn jetzt nachahmen, aber das Meinen erscheint als eine ganz ungreifbare, feine Atmosphäre des Sprechens und Handelns. (Ein verdächtiges Bild!)
28. Im Laufe eines Gesprächs will ich auf etwas zeigen; ich habe bereits den Anfang einer Zeigebewegung gemacht; führe sie aber nicht aus. Später sage ich: "Ich wollte damals darauf zeigen. Ich erinnere mich noch deutlich, daß ich schon den Finger aufgehoben hatte." In dem Strom dieser Vorgänge, Gedanken und Empfindungen war dies der Anfang einer Gebärde des Zeigens.
Ja, wenn ich die ganze Gebärde machte und sagte "Er liegt dort drüben", so wäre das kein Zeigen, wenn nicht diese Worte zu einer Sprache gehörten.
29. "Du hast mit der Hand eine Bewegung gemacht; hast du etwas damit gemeint ?—Ich dachte, du meintest, ich solle zu dir kommen."
Also er konnte etwas meinen oder auch nichts meinen. Und wenn das erstere: dann eben seine Handbewegung,—oder etwas Anderes? Hat er mit seinem Ausdruck etwas Anderes als diesen gemeint, oder hat er nur seinen Ausdruck—gemeint?
30. Könnte man auch antworten: "Ich habe etwas mit dieser Bewegung gemeint, was ich nur durch diese Bewegung ausdrücken kann"? (Musik, musikalischer Gedanke.)
31. "Freilich dachte ich an ihn: ich habe ihn vor mir gesehen!"—Aber nicht nach seinem Bilde erkannt.
32. Stelle dir einen deiner Bekannten vor!——Nun sage, wer es war!—Manchmal kommt das Bild zuerst und der Name danach. Aber errate ich den Namen nach der Ähnlichkeit des Bildes?—Und wenn nun der Name dem Bild erst nachfolgt,—war die Vorstellung jenes Menschen schon mit dem Bild da, oder war sie erst mit dem Namen vollständig? Ich habe ja auf den Namen nicht aus dem Bild geschlossen; und eben darum kann ich sagen, die Vorstellung von ihm sei schon mit dem Bild gekommen.
33. Es ist, wie wenn man eine Tendenz, eine Bereitschaft erlebte (James). Und warum soll ich es nicht so nennen? (Und manche würden auch, was da geschieht, durch Innervationen von Muskeln, Ansätze zu Bewegungen oder gar Vorstellungen von ihnen erklären.) Nur mußt du das Erlebnis einer Tendenz nicht unter dem Bild eines nicht ganz fertigen Erlebnisses ansehen.
Es scheint uns oft, als mache der Geist beim Verstehen der Bedeutung kleine rudimentäre Bewegungen, wie ein Unschlüssiger, der nicht weiß, welchen Weg er gehen soll—gehe also das Gebiet der möglichen Anwendungen ab.
34. Denke dir Menschen, die von Kind auf mit großer Schnelligkeit kritzeln, während sie reden: was sie reden, gleichsam illustrieren.
Muß ich annehmen, daß, wer aus der Vorstellung oder Erinnerung etwas zeichnet oder beschreibt oder nachahmt, seine Darstellung von irgend etwas abliest?!—Was spricht dafür?
35. Gedanken erraten. Spielkarten liegen auf einem Tisch. Ich will, daß der Andre eine von ihnen berühren soll. Ich schließe die Augen und denke an eine dieser Karten; der Andre soll erraten, welche ich meine.—Er läßt sich darauf etwa eine Karte einfallen und wünscht dabei, meine Meinung zu treffen. Er berührt die Karte, und ich sage "Ja, die war's", oder sie war's nicht. Eine Variante dieses Spiels wäre es, daß ich auf eine bestimmte Karte schaue, so zwar, daß der Andre die Richtung meines Blicks nicht sieht, und daß er nun die Karte erraten muß, auf die ich schaue. Daß dies eine Variante des ersten Spiels ist, ist wichtig. Es kann hier wichtig sein, wie ich an die Karte denke, weil es sich zeigen könnte, daß davon die Zuverlässigkeit des Erratens abhängt. Sage ich aber im gewöhnlichen Leben "Ich dachte soeben an N", so fragt man mich nicht "Wie hast du an ihn gedacht?".
36. Man möchte fragen: "Hätte einer, der in dein Inneres zu sehen imstande wäre, dort sehen können, daß du das sagen wolltest?"
Angenommen, ich hätte mir meinen Vorsatz auf einem Zettel notiert, so hätte ein Andrer meinem Vorsatz dort lesen können. Und kann ich mir denken, daß er ihn auf irgend einem Wege hätte sicherer erfahren können, als so? Gewiß nicht.
37. (Über einem Musikstück steht, vom Komponisten darübergeschrieben, ![]() = 88, aber um es heute richtig zu spielen, muß es
= 88, aber um es heute richtig zu spielen, muß es ![]() = 94 gespielt werden: welches ist das vom Komponisten gemeinte Tempo?)
= 94 gespielt werden: welches ist das vom Komponisten gemeinte Tempo?)
38. Unterbrich einen Menschen im gänzlich unvorbereiteten und fließenden Reden. Dann frag ihn, was er sagen wollte, und er wird in vielen Fällen den angefangenen Satz fortführen können.—"Dazu mußte ihm schon vorgeschwebt haben, was er sagen wollte."—Ist nicht vielleicht jenes Phänomen der Grund, warum wir sagen, die Fortsetzung hätte ihm vorgeschwebt?
39. Ist es aber nicht sonderbar, daß es so eine Reaktion, so ein Geständnis der Intention gibt? Ist es nicht ein höchst merkwürdiges Sprachinstrument? Was ist eigentlich merkwürdig daran? Nun,—es ist schwer vorstellbar, wie der Mensch diesen Wortgebrauch lernt. Er ist gar so subtil.
40. Aber ist er wirklich subtiler, als der der Worte "Ich habe mir ihn vorgestellt" z. B.? Ja, merkwürdig, sonderbar ist jede solche Sprachverwendung, wenn man nur auf die Betrachtung der Beschreibungen physikalischer Gegenstände eingestellt ist.
41. Sage ich "Ich wollte damals das und das tun", und beruht diese Aussage auf den Gedanken, Vorstellungen, etc., an die ich mich erinnere, so muß ein Andrer, dem ich nur diese Gedanken, Vorstellungen etc. mitteile, daraus mit ebensolcher Sicherheit schließen können, ich hätte damals das und das tun wollen.—Er könnte das aber oft nicht. Ja, schlösse ich selbst nun aus dieser Evidenz auf meine Absicht, so würde der Andre mit Recht sagen, dieser Schluß sei sehr unsicher.
42. Und wie lernt [das Kind] den Ausdruck gebrauchen "Ich war damals im Begriffe zu werfen"? Und wie weiß man, daß es damals wirklich in jenem Seelenzustand war, den ich "im Begriffe sein ..." nenne?
43. Wie nun, wenn ein Mensch den Ausdruck "Ich war damals im Begriffe ....", oder "Ich wollte damals ...." nie gebrauchte und seinen Gebrauch nicht erlernen könnte? Der Mensch kann doch viel denken, ohne das zu denken. Er kann ein großes Gebiet der Sprachspiele beherrschen, ohne dieses zu beherrschen.
Ist es aber dann nicht sonderbar, daß wir in dieser Art defekten Menschen nicht begegnen, bei aller der Verschiedenheit der Menschen? Oder finden sich eben diese Leute unter den Geistesschwachen, und es wird nur nicht genügend beobachtet, welcher Sprachverwendungen solche fähig sind und welcher nicht?
44. "Ich hatte die Absicht ...." drückt nicht die Erinnerung an ein Erlebnis aus. (So wenig wie: "Ich war im Begriffe, ....")
45. Absicht (Intention) ist weder Gemütsbewegung, Stimmung, noch Empfindung oder Vorstellung. Sie ist kein Bewußtseinszustand. Sie hat nicht echte Dauer.
46. "Ich habe die Absicht, morgen zu verreisen."—Wann hast du die Absicht? Die ganze Zeit; oder intermittierend?
47. Schau in die Lade, in der du sie zu finden glaubst. Die Lade ist leer.—Ich glaube, du hast sie unter den Empfindungen gesucht.
Überlege, was das eigentlich heißen würde "eine Absicht intermittierend haben". Es hieße etwa: die Absicht haben, sie fallen lassen, sie wieder aufnehmen u. s. f.
48. Unter was für Umständen sagt man "Diese Vorrichtung ist eine Bremse, funktioniert aber nicht"? Das heißt doch: sie erfüllt ihren Zweck nicht. Worin liegt es, daß sie diesen Zweck hat? Man könnte auch sagen: "Es war die Absicht, daß dies als Bremse wirken sollte." Wessen Absicht? Hier entschwindet uns die Absicht als Zustand der Seele gänzlich.
Könnte man sich nicht auch das denken, daß mehrere Leute eine Absicht hätten, ausführten, ohne daß einer von ihnen sie hat? So kann eine Regierung eine Absicht haben, die kein Mensch hat.
49. Es könnte ein Verbum geben, welches bedeutet: die Absicht durch Worte oder andere Zeichen laut oder in Gedanken aussprechen. Dies Zeitwort wäre nicht gleichbedeutend unserem "beabsichtigen".
Es könnte ein Verbum geben, welches bedeutet: einer Absicht gemäß handeln; und dieses wäre auch nicht gleichbedeutend unserem "beabsichtigen".
Wieder ein Anderes könnte bedeuten: über eine Absicht brüten; oder sie im Kopfe hin und her wälzen.
50. Man kann einen im Denken stören,—aber im Beabsichtigen?——Im Planen wohl. Auch im Festhalten einer Absicht, nämlich im Denken oder Handeln.
51. Anwendung des Imperativs. Vergleiche die Befehle:
- Heb den Arm!
- Stell dir ..... vor!
- Rechne ..... im Kopf!
- Überlege dir .....!
- Konzentrier deine Aufmerksamkeit auf .....!
- Sieh diese Figur als Würfel an!
mit diesen:
- Beabsichtige .....!
- Meine mit diesen Worten .....!
- Vermute, daß es sich so verhält!
- Glaube, daß es so ist!
- Sei der festen Überzeugung .....!
- Erinnere dich daran, daß dies geschehen ist!
- Zweifle daran, ob es geschehen ist!
- Hoffe auf seine Wiederkehr!
Ist das der Unterschied, daß die ersten willkürliche, die zweiten unwillkürliche Bewegungen des Geistes sind? Eher kann ich sagen, die Verben der zweiten Gruppe bezeichnen keine Handlungen. (Vergleiche damit den Befehl: "Lache herzlich über diesen Witz!")
52. Kann man jemandem befehlen, einen Satz zu verstehen? Warum kann man einem nicht befehlen: "Versteh das!"? Könnte ich nicht den Befehl "Versteh diesen griechischen Satz!" dadurch befolgen, daß ich Griechisch lernte?——Ähnlich: Man kann sagen "Rufe dir Schmerzen hervor!", aber nicht "Habe Schmerzen!" Man sagt: "Versetz dich in diesen Zustand!" aber nicht: "Sei in diesem Zustand!"
53. Ich erwarte jeden Augenblick eine Explosion. Ich bin nicht imstande, einer andern Sache meine volle Aufmerksamkeit zu schenken; schaue in ein Buch, aber ohne zu lesen. Auf die Frage, warum ich zerstreut oder nervös scheine, sage ich, ich erwarte en Augenblick die Explosion.—Wie war es nun: Beschrieb dieser Satz eben jenes Verhalten? Aber wie unterscheidet sich dann der Vorgang des Erwartens der Explosion vom Vorgang des Erwartens eines ganz andern Ereignisses, z. B. eines bestimmten Signals? Und wie unterscheidet sich die Erwartung eines Signals von der Erwartung eines um weniges verschiedenen Signals? Oder war meine Handlungsweise nur Nebenerscheinung der eigentlichen Erwartung, und diese ein besonderer geistiger Vorgang? Und war dieser Vorgang homogen oder gegliedert wie ein Satz (mit internen Anfang und Ende)? Wie weiß aber der, in dem er vorgeht, welches Ereignisses Erwartung der Vorgang ist? Er scheint nämlich nicht darüber im Ungewissen. Es ist nicht, als konstatierte er einen seelischen oder andern Zustand und machte eine Vermutung über dessen Ursache. Er mag wohl sagen "Ich weiß nicht, ist es nur diese Erwartung, die mich heute so unruhig mache", aber er wird nicht sagen: "Ich weiß nicht, ist dieser Seelenzustand, in dem ich jetzt bin, die Erwartung einer Explosion, oder von etwas Anderm."
Die Aussage "Ich erwarte jeden Moment einen Knall" ist eine Äußerung der Erwartung. Diese Wortreaktion ist der Ausschlag des Zeigers, der den Gegenstand der Erwartung anzeigt.
54. Es scheint: die Erwartung und die Tatsache, die die Erwartung befriedigt, passen doch irgendwie zusammen. Man möge nun eine Erwartung beschreiben und eine Tatsache, die zusammen. passen, damit man sieht, worin diese Übereinstimmung besteht. Da denkt man sofort an das Passen einer Vollform in eine entsprechende Hohlform. Aber wenn man diese beiden beschreiben will, so sieht man, daß, soweit sie passen, eine Beschreibung für beide gilt. (Vergleiche dagegen, was es heißt "Diese Hose paßt nicht zu diesem Rock".)
55. Wie alles Metaphysische ist die Harmonie zwischen Gedanken und Wirklichkeit in der Grammatik der Sprache aufzufinden.
56. Mein Gedanke ist hier: Wenn Einer die Erwartung selbst sehen könnte—er müßte sehen, was erwartet wird. (So aber, daß es nicht noch einer Projektionsmethode, Vergleichsmethode bedürfte, um von dem, was er sieht, zu der Tatsache zu kommen, die erwartet wird.)
Aber so ist es ja auch: Wer den Ausdruck der Erwartung sieht, sieht, 'was erwartet wird'.
57. Der Gedanke, daß uns erst das Finden zeigt, was wir gesucht, erst die Erfüllung des Wunsches, was wir gewünscht haben, heißt, den Vorgang so beurteilen, wie die Symptome der Erwartung oder des Suchens bei einem Andern. Ich sehe ihn unruhig in seinem Zimmer auf und ab gehen; da kommt jemand zur Tür herein, und er wird ruhig und gibt Zeichen der Befriedigung. Und nun sage ich "Er hat offenbar diesen Menschen erwartet".
58. Wir sagen, der Ausdruck der Erwartung 'beschreibe' die erwartete Tatsache und denken an sie, wie an einen Gegenstand oder Komplex, der als Erfüllung der Erwartung in die Erscheinung tritt.—Aber der Erwartete ist nicht die Erfüllung, sondern: daß er kommt.
Der Fehler ist tief in unserer Sprache verankert: Wir sagen "ich erwarte ihn" und "ich erwarte sein Kommen" und "ich erwarte, daß er kommt".
59. Es ist uns schwer, von dem Vergleich loszukommen: Der Mensch tritt ein—das Ereignis tritt ein. Als wäre das Ereignis schon vorgebildet vor der Tür der Wirklichkeit und würde nun in diese (wie in ein Zimmer) eintreten.
60. Die Realität ist keine Eigenschaft, die dem Erwarteten noch fehlt, und die nun hinzutritt, wenn die Erwartung eintritt.—Die Realität ist auch nicht wie das Tageslicht, das den Dingen erst Farbe gibt, wenn sie im Dunkeln schon gleichsam farblos vorhanden sind.
61. Man kann vom Träger eines Namens sagen, daß er nicht existiert; und das ist natürlich keine Tätigkeit, obwohl man es mit einer vergleichen könnte und sagen: er müsse doch dabei sein, wenn er nicht existiert. (Und das ist von einem Philosophen bestimmt schon einmal geschrieben worden.)
62. Das schattenhafte Antizipieren der Tatsache besteht darin, daß wir jetzt denken können, daß das eintreffen wird, was erst eintreffen wird. Oder, wie es irreführenderweise heißt: daß wir jetzt das (oder an das) denken können, was erst eintreffen wird.
63. Mancher wird vielleicht sagen wollen "Die Erwartung ist ein Gedanke." Das entspricht offenbar einem Gebrauch des Wortes "erwarten". Und wir wollen uns nur erinnern, daß der Vorgang des Gedankens sehr verschiedenerlei sein kann.
64. Ich pfeife, und jemand fragt mich, warum ich guter Dinge bin. Ich antworte, "Ich hoffe, N wird heute kommen."—Aber während ich pfiff, dachte ich nicht an ihn. Und doch wäre es falsch zu sagen: ich hätte aufgehört zu hoffen, als ich zu pfeifen anfing.
65. Wenn ich sage "Ich erwarte ....."—ist das die Feststellung: die Situation, meine Handlungen, Gedanken etc. seien die des Erwartens dieses Ereignisses; oder gehören die Worte "Ich erwarte ....." zum Vorgang des Erwartens ?
Unter gewissen Umständen werden diese Worte heißen (ersetzt werden können durch) "Ich glaube, das und das wird eintreten". Manchmal auch: "Mach dich darauf gefaßt, daß ....."
66. Die psychologischen—trivialen—Erörterungen über Erwartung, Assoziation u.s.w., lassen immer das eigentlich Merkwürdige aus, und man merkt ihnen an, daß sie herumreden, ohne den springenden Punkt zu berühren.
67. Eine Erwartung ist in einer Situation eingebettet, aus der sie entspringt. Die Erwartung einer Explosion kann z.B. aus einer Situation entspringen, in der eine Explosion zu erwarten ist. Der sie erwartet, hatte zwei Leute flüstern hören: "Morgen um zehn Uhr wird die Lunte angebrannt". Dann denkt er: vielleicht will jemand hier ein Haus in die Luft sprengen. Gegen zehn Uhr wird er unruhig, fährt bei jedem Lärm zusammen, und endlich antwortet er auf die Frage, warum er nervös sei: "Ich erwarte ....". Diese Antwort wird z. B. sein Benehmen verständlich machen. Sie wird uns auch in den Stand setzen, uns seine Gedanken und Gefühle auszumalen.
68. Die Erfüllung der Erwartung besteht nicht darin, daß ein Drittes geschieht, das man, außer eben als "die Erfüllung dieser Erwartung" auch noch anders beschreiben könnte, also z. B. als ein Gefühl der Befriedigung oder der Freude oder wie immer. Die Erwartung, daß etwas der Fall sein wird, ist das Gleiche, wie die Erwartung der Erfüllung jener Erwartung. [Randbemerkung: Erwartung dessen was nicht ist.]
69. Sokrates zu Theaitetos: "Und wer vorstellt, sollte nicht etwas vorstellen?"—Th.: "Notwendig".—Sok.: "Und wer etwas vorstellt, nichts Wirkliches?"—Th.: "So scheint es."
Setzen wir in diesem Argument statt des Wortes "vorstellen" etwa das Wort "töten", so gibt es eine Regel für den Gebrauch dieses Worts: es hat keinen Sinn zu sagen "Ich töte etwas, was nicht existiert". Ich kann mir einen Hirsch auf dieser Wiese vorstellen, der nicht da ist, aber keinen töten, der nicht da ist. Und "sich einen Hirsch auf dieser Wiese vorstellen", heißt: sich vorstellen, daß ein Hirsch da ist. Einen Hirsch töten aber heißt nicht: töten, daß etc. Wenn aber jemand sagt "Damit ich mir einen Hirsch vorstellen kann, muß es ihn doch in einem gewissen Sinne geben"—so ist die Antwort: nein, es muß ihn dazu in keinem Sinne geben. Und wenn geantwortet würde: "Aber die braune Farbe z. B. muß es doch geben, damit ich sie mir vorstellen kann",—so ist zu sagen: "es gibt die braune Farbe", heißt überhaupt nichts; außer etwa, daß sie da oder dort als Färbung eines Gegenstands vorhanden ist; und das ist nicht nötig, damit ich mir einen braunen Hirsch vorstellen kann.
70. Etwas tun können, erscheint wie ein Schatten des wirklichen Tuns, gerade wie der Sinn des Satzes als Schatten einer Tatsache, oder das Verstehen des Befehls als Schatten seiner Ausführung, Im Befehl wirft die Tatsache gleichsam "ihren Schatten schon voraus". Dieser Schatten aber, was immer er wäre, ist nicht das Ereignis.
71. Vergleiche die Anwendungen von:
- "Ich habe seit gestern Schmerzen."
- "Ich habe ihn seit gestern erwartet."
- "Ich wußte seit gestern."
- "Ich kann seit gestern integrieren."
72. Der gemeinsame Unterschied aller Bewußtseinszustände von den Dispositionen scheint mir zu sein, daß man sich nicht durch Stichproben überzeugen kann, ob sie noch andauern.
73. Man muß manchen Satz öfter lesen, um ihn als Satz zu verstehen.
74. Ein Satz sei mir in einer Chiffer gegeben und auch ihr Schlüssel; dann ist mir natürlich in einer Beziehung alles zum Verständnis des Satzes gegeben. Und doch würde ich auf die Frage "Verstehst du diesen Satz?" antworten: Nein, noch nicht; ich muß ihn erst entziffern. Und erst, wenn ich ihn z. B. ins Deutsche übertragen hätte, würde ich sagen "Jetzt verstehe ich ihn".
Wenn man nun die Frage stellt "In welchem Moment der Übertragung verstehe ich nun den Satz?", würde man einen Einblick in das Wesen dessen erhalten, was wir "verstehen" nennen.
75. Ich kann auf den Verlauf meiner Schmerzen achten; aber nicht ebenso auf den meines Glaubens, meiner Übersetzung oder meines Wissens.
76. Man kann die Fortdauer einer Erscheinung durch ununterbrochene Beobachtung feststellen oder durch Proben. Das Beobachten der Dauer kann ununterbrochen oder unterbrochen sein.
77. Wie beobachte ich mein Wissen, meine Meinungen? Und andererseits, ein Nachbild, einen Schmerz? Gibt es ein ununterbrochenes Beobachten meiner Fähigkeit die Multiplikation .... auszuführen?
78. Ist "Ich hoffe ...." eine Beschreibung eines Seelenzustandes? Ein Seelenzustand hat eine Dauer. "Ich habe den ganzen Tag gehofft....", ist also so eine Beschreibung. Sage ich aber einem "Ich hoffe, du kommst"—wie, wenn er mich fragte "Wie lange hoffst du es"? Ist die Antwort: "Ich hoffe, während ich's sage"? Angenommen ich hätte auf diese Frage irgend eine Antwort, wäre sie nicht für den Zweck der Worte "Ich hoffe, du wirst kommen" ganz irrelevant?
79. Man sagt "Ich hoffe, du wirst kommen", aber nicht "Ich glaube, ich hoffe, du wirst kommen"; wohl aber wäre es möglich zu sagen: "Ich glaube, ich hoffe noch immer, er werde kommen".
80. Was ist die Vergangenheitsform von "Nicht wahr, du kommst!"?
81. Wo es echte Dauer gibt, da kann man einem sagen: "Merk auf und gib mir ein Zeichen, wenn das Bild, das Erlebte, das Geräusch etc. sich ändert."
Es gibt da überhaupt ein Aufmerken. Während man nicht das Vergessen des Gewußten und dergleichen mit der Aufmerksamkeit verfolgen kann. [Randbemerkung: Stimmt nicht, denn man kann auch die eigenen Vorstellungen nicht mit der Aufmerksamkeit verfolgen.]
82. Denk an das Sprachspiel: Bestimm mit der Stoppuhr, wie lange der Eindruck dauert. Man könnte so nicht die Dauer des Wissens, Könnens, Verstehens bestimmen.
83. "Aber die Verschiedenheit von Wissen und Hören liegt doch nicht einfach in so einem Merkmal, wie die Art ihrer Dauer. Sie sind doch ganz und gar grundverschieden!" Freilich. Aber man kann eben nicht sagen: "Wisse und höre, und du wirst den Unterschied merken!"
84. "Schmerz ist ein Bewußtseinszustand, Verstehen nicht."—"Nun, ich fühle eben das Verstehen nicht."—Aber diese Erklärung taugt nichts. Es wäre auch keine Erklärung zu sagen: Was man in irgend einem Sinne fühlt, sei ein Bewußtseinszustand. Das hiebe ja nur: Bewußtseinszustand = Gefühl. (Man hätte nur ein Wort durch ein anderes ersetzt.)
85. Man sagt wohl überhaupt kaum, man habe etwas seit gestern "ununterbrochen" geglaubt, verstanden oder beabsichtigt. Eine Unterbrechung des Glaubens wäre eine Zeit des Unglaubens, nicht z. B. die Abwendung der Aufmerksamkeit von dem Geglaubten, z. B. der Schlaf.
(Unterschied zwischen 'knowing' und 'being aware of'.)
86. Das Wichtigste ist hier dies: es besteht ein Unterschied; man merkt den Unterschied 'der ein kategorischer ist'—ohne sagen zu können, worin er besteht. Das ist der Fall, in dem man gewöhnlich sagt, man erkenne den Unterschied eben durch Introspektion.
87. Das ist wohl der Punkt, an dem man sagt, man könne dem Andern eben nur die Form mitteilen, nicht aber den Inhalt.—So redet man also zu sich selbst über den Inhalt.——Wie 'beziehen' sich aber meine Worte auf den mir bewußten Inhalt? und zu welchem Zweck?
88. Es ist sehr merkwürdig, daß die Vorgänge beim Denken uns so gut wie nie interessieren. Es ist merkwürdig, aber nicht seltsam.
89. (Gedanken, gleichsam nur Winke.)
Ist es hier nicht wie beim Kunstrechner?—Er hat richtig gerechnet, wenn das Richtige herauskam. Was in ihm vorging, kann er vielleicht selbst nicht sagen. Und hörten wir's, so erschiene es vielleicht wie ein seltsames Zerrbild einer Rechnung.
90. Was weiß ich von den inneren Vorgängen Eines, der mit Aufmerksamkeit einen Satz liest? Und kann er mir sie beschreiben, nachdem er's getan hat; und ist, was er etwa beschreibt, eben der charakteristische Vorgang der Aufmerksamkeit?
91. Frage: Welche Wirkung will ich erzielen, wenn ich Einem sage "Lies aufmerksam!"? Etwa, daß ihm das und jenes auffällt, er davon berichten kann.—Wieder könnte man, glaube ich, sagen, daß, wer einen Satz mit Aufmerksamkeit liest, oft von Vorgängen in seinem Geist, Vorstellungen etwa, wird berichten können. Aber das heißt nicht, daß diese Vorgänge "Aufmerksamkeit" hießen.
92. "Hast du den Satz denkend gelesen?"—"Ja, ich habe ihn denkend gelesen; jedes Wort war mir wichtig."
Das ist nicht das gewöhnliche Erlebnis. Man hört sich für gewöhnlich nicht halb erstaunt etwas reden; folgt der eigenen Rede nicht mit der Aufmerksamkeit; denn man redet für gewöhnlich eben willkürlich, nicht unwillkürlich.
93. Wenn ein sonst normaler Mensch unter normalen Umständen ein normales Gespräch führt, und ich gefragt würde, wie sich in so einem Falle der Denkende vom Nichtdenkenden unterschiede,——ich wüßte nicht zu antworten. Und ich könnte gewiß nicht sagen, daß der Unterschied in etwas liegt, was während des Sprechens vor sich ginge oder nicht vor sich ginge.
94. Die Grenzlinie zwischen 'denken' und 'nicht denken', die hier gezogen würde, liefe zwischen zwei Zuständen, die sich durch nichts einem Spiel der Vorstellungen auch nur Ähnliches unterschieden. (Denn das Spiel der Vorstellungen ist ja doch das Vorbild, wonach man sich das Denken denken möchte.)
95. Nur unter ganz speziellen Umständen tritt die Frage auf, ob denkend geredet wurde oder nicht.
96. Ja, wenn man von einer Erfahrung des Denkens spricht, so ist die Erfahrung des Redens so gut wie jede andere. Aber der Begriff 'denken' ist kein Erfahrungsbegriff. Denn man vergleicht Gedanken nicht, wie man Erfahrungen vergleicht.
97. Was man nachmacht, ist etwa der Ton der Rede, die Miene und dergleichen, und das genügt uns. Das beweist, daß hier die wichtigen Begleitphänomene der Rede liegen.
98. Sagen wir, es denke jeder, der sinnvoll spricht? Z. B. der Bauende im Sprachspiel No.2? Könnten wir uns nicht das Bauen und Rufen der Wörter etc. in einer Umgebung denken, in der wir es mit einem Denken nicht im entferntesten in Zusammenhang brachten?
99. (Zum Sprachspiel No.2) "Du setzt eben stillschweigend schon voraus, daß diese Menschen denken; daß sie in dieser Beziehung den uns bekannten Menschen gleichen; daß sie jenes Sprachspiel nicht rein mechanisch betreiben. Denn stelltest du dir vor, sie täten's, so würdest du's selbst nicht den Gebrauch einer rudimentären Sprache nennen."
Was soll ich nun dem antworten? Es ist natürlich wahr, das Leben jener Menschen muß dem unsern in vieler Beziehung gleichen, und ich habe über diese Ähnlichkeiten nichts gesagt. Das Wichtige aber ist, daß ihre Sprache, wie auch ihr Denken, rudimentär sein kann, daß es ein 'primitives Denken' gibt, welches durch ein primitives Verhalten zu beschreiben ist. Die Umgebung ist nicht die 'Denkbegleitung' des Sprechens.
100. Denken wir uns, daß einer eine Arbeit verrichtet, in der es ein Vergleichen, Versuchen, Wahlen gibt. Er stellt etwa einen Gebrauchsgegenstand aus gewissen Materialstücken mit gegebenen Werkzeugen her. Immer wieder entsteht das Problem "Soll ich dies Stück dazu nehmen?"—Das Stück wird verworfen, ein anderes versucht. Stücke werden versuchsweise zusammengestellt, auseinandergenommen; es wird nach einem passenden gesucht etc., etc. Ich denke mir nun diesen ganzen Hergang gefilmt. Der Arbeitende gibt etwa auch Laute von sich, wie "hm" oder "ha!" Sozusagen Laute des Zögerns, des plötzlichen Findens, des Entschlusses, der Zufriedenheit, der Unzufriedenheit. Aber kein Wort wird geredet. Jene Laute mögen im Film aufgenommen werden. Der Film wird mir vorgeführt, und ich erfinde nun ein Selbstgespräch des Arbeitenden, welches zu seiner Arbeitsweise, dem Rhythmus seiner Arbeit, seinem Mienenspiel, seinen Gebärden und Naturlauten paßt, welches all dem entspricht. Ich lasse ihn also manchmal sagen "Nein, das Stück ist zu lang, vielleicht paßt ein anderes besser."——Oder "Was soll ich jetzt tun?"——"Ich hab's!"——Oder "Das ist ganz gut" etc.
Wenn der Arbeitende reden kann,—wäre es eine Verfälschung des wirklichen Vorgangs, wenn er ihn genau beschriebe und etwa sagte: "Dann dachte ich: Nein, das geht nicht; ich muß es anders versuchen." u.s.w.—obwohl er während der Arbeit nicht gesprochen und sich auch diese Worte nicht vorgestellt hatte?
Ich will sagen: Kann er nicht seine wortlosen Gedanken später in Worten wiedergeben? So zwar, daß wir, die den Arbeitsvorgang sähen, mit dieser Wiedergabe einverstanden sein könnten?—Umsomehr, wenn wir den Mann nicht nur einmal, sondern öfters bei der Arbeit zugesehen hätten?
101. Wir könnten natürlich sein 'Denken' von der Tätigkeit nicht trennen. Das Denken ist eben keine Begleitung der Arbeit; so wenig wie der denkenden Rede.
102. Wenn wir Wesen bei der Arbeit sähen, deren Arbeitsrhythmus, deren Mienenspiel etc. dem unseren ähnlich wäre, nur daß sie nicht sprächen, dann würden wir vielleicht sagen, sie dächten, überlegten, machten Entscheidungen. Es wäre eben da viel, was dem Tun des gewöhnlichen Menschen entspricht. Und es ist nicht zu entscheiden, wie genau die Entsprechung sein muß, damit wir den Begriff 'denken' auch bei ihnen anzuwenden ein Recht haben.
103. Und wozu sollen wir auch diese Entscheidung fallen?
Wir werden einen wichtigen Unterschied machen zwischen Wesen, die eine Arbeit, selbst eine komplizierte, 'mechanisch' zu verrichten lernen können und solchen, die bei der Arbeit probieren, vergleichen——Was aber "probieren" und "vergleichen" zu nennen ist, kann ich nur wieder an Beispielen erklären, und diese Beispiele werden unserm Leben oder einem, das dem unsern ähnlich ist, entnommen sein.
104. Hat er etwa spielend oder durch Zufall eine Kombination gemacht und verwendet sie nun als Methode, das und jenes zu tun, so werden wir sagen, er denke.—Beim Überlegen würde er Mittel und Wege an seinem geistigen Auge vorbeiziehen lassen. Aber dazu muß er schon welche im Vorrat haben. Das Denken gibt ihm die Möglichkeit zur Vervollkommnung seiner Methoden. Oder vielmehr: Er 'denkt', wenn er in bestimmter Art und Weise seine Methode vervollkommnet. [Randbemerkung: Wie schaut denn das Forschen aus?]
105. Man könnte auch sagen: einer denkt, wenn er in bestimmter Weise lernt.
106. Und auch dies (könnte man sagen): Wer bei der Arbeit denkt, der wird oft Hilfstätigkeiten in sie einschalten. Das Wort "denken" nun bezeichnet nicht diese Hilfstätigkeiten, wie Denken ja auch nicht Reden ist. Obwohl der Begriff 'denken' nach Art einer imaginären Hilfstätigkeit gebildet ist. (So wie man sagen könnte, der Begriff des Differentialquotienten sei nach Art eines idealen Quotienten gebildet.)
107. Diese Hilfstätigkeiten sind nicht das Denken; aber man stellt sich das Denken vor als den Strom der unter der Oberfläche dieser Hilfsmittel fließen muß, wenn sie nicht doch nur mechanische Handlungen sein sollen.
108. Nimm an, es handle sich um Wesen (menschenähnliche Tiere), die wir als Sklaven benützen, kaufen und verkaufen. Sie können nicht sprechen lernen, wohl aber kann man die begabteren unter ihnen zu oft recht komplizierten Arbeiten erziehen; und manche von diesen arbeiten 'denkend', andre bloß mechanisch. Für einen Denkenden zahlen wir mehr, als für einen bloß mechanisch Geschickten.
109. Wenn es nur ganz wenige Menschen gäbe, die die Antwort auf eine Rechenaufgabe finden könnten, ohne zu sprechen oder zu schreiben, könnte man diese nicht zum Zeugnis dafür anführen, daß man auch ohne Zeichen rechnen könne. Weil es nämlich nicht klar wäre, daß diese Leute überhaupt 'rechnen'. Ebenso kann auch das Zeugnis des Ballard (bei James) einen nicht davon überzeugen, daß man ohne Sprache denken könne.
Ja, warum soll man, wo keine Sprache gebraucht wird, vom 'Denken' reden? Tut man's, so zeigt das eben etwas über den Begriff des Denkens.
110. 'Denken', ein weit verzweigter Begriff. Ein Begriff, der viele Lebensäußerungen in sich verbindet. Die Denk-phänomene liegen weit auseinander.
111. Wir sind auf die Aufgabe gar nicht gefaßt, den Gebrauch des Wortes "denken" z. B. zu beschreiben. (Und warum sollten wir's sein? Wozu ist so eine Beschreibung nütze?)
Und die naive Vorstellung, die man sich von ihm macht, entspricht gar nicht der Wirklichkeit. Wir erwarten uns eine glatte, regelmäßige Kontur und kriegen eine zerfetzte zu sehen. Hier könnte man wirklich sagen, wir hätten uns ein falsches Bild gemacht.
112. Es ist von diesem Wort nicht zu erwarten, daß es eine einheitliche Verwendung habe; es ist vielmehr das Gegenteil zu erwarten.
113. Woher nehmen wir den Begriff 'denken', den wir hier betrachten wollen? Aus der Alltagssprache. Was unsrer Aufmerksamkeit zuerst ihre Richtung gibt, ist das Wort "denken". Aber der Gebrauch dieses Worts ist verworren. Und wir können es nicht anders erwarten. Und das läßt sich natürlich von allen psychologischen Verben sagen. Ihre Verwendung ist nicht so klar und so leicht zu übersehen, wie die der Wörter der Mechanik z. B.
114. Man lernt das Wort "denken", d. i. seinen Gebrauch, unter gewissen Umständen, die man aber nicht beschreiben lernt.
115. Aber ich kann einen Menschen den Gebrauch des Wortes lehren! Denn dazu ist ein Beschreiben jener Umstände nicht nötig.
116. Ich lehre ihn eben das Wort unter bestimmten Umständen.
117. Man lernt es etwa nur vom Menschen sagen, es von ihm behaupten oder leugnen. Die Frage "Denkt ein Fisch?" existiert unter seinen Sprachanwendungen nicht, wird nicht gestellt. (Was kann natürlicher sein, als so ein Zustand, so eine Sprachverwendung?)
118. "An diesen Fall hat niemand gedacht"—kann man sagen. Ich kann zwar nicht die Bedingungen aufzählen, unter denen das Wort "denken" zu gebrauchen ist,—aber, wenn ein Umstand den Gebrauch zweifelhaft macht, so kann ich's sagen und auch, wie die Lage von der gewöhnlichen abweicht.
119. Wenn ich in einem bestimmten Zimmer eine bestimmte Tätigkeit auszuführen gelernt habe (das Aufräumen des Zimmers etwa) und diese Technik beherrsche, so folgt doch nicht, daß ich bereit sein müsse, die Einrichtung des Zimmers zu beschreiben; auch wenn ich jede Veränderung in ihr gleich merken würde und auch sofort beschreiben könnte.
120. "Dieses Gesetz wurde nicht in Voraussicht solcher Fälle gegeben." Ist es darum sinnlos?
121. Es wäre doch sehr wohl denkbar, daß einer sich genau in einer Stadt auskennt, d. h., von jedem Ort der Stadt zu jedem andern mit Sicherheit den kürzesten Weg fände,—und dennoch ganz außer Stande wäre, einen Plan der Stadt zu zeichnen. Daß er, sobald er es versucht, nur gänzlich Falsches hervorbringt. (Unser Begriff vom 'Instinkt'.)
122. Bedenke, unsere Sprache könnte verschiedene Wörter besitzen: fürs 'laute Denken'; fürs denkende Selbstgespräch in der Vorstellung; fürs Innehalten, wobei irgend etwas uns vorschwebt, woraufhin wir aber die Antwort mit Sicherheit geben können.
Ein Wort für den Gedanken, der im Satz ausgedrückt ist; eines für den Gedankenblitz, den ich später 'in Worte kleiden' kann, eines für das denkende Arbeiten ohne Worte.
123. "Denken ist eine geistige Tätigkeit."——Denken ist keine körperliche Tätigkeit. Ist Denken eine Tätigkeit? Nun, man kann einem befehlen "denk darüber nach!". Wenn aber einer in Befolgung dieses Befehls zu sich selbst oder auch zum Andern spricht, verrichtet er da zwei Tätigkeiten?
124. Die Anteilnahme an dem Gesprochenen hat ihre spezifischen Zeichen. Sie hat auch ihre spezifischen Folgen und Vorbedingungen. Die Anteilnahme ist ein Erlebtes: man sagt sie von sich selbst, nicht auf Grund einer Beobachtung, aus. Sie ist keine Begleitung des Gesprochenen. Wodurch wäre, was den Satz begleitet, eine Anteilnahme am Inhalt dieses Satzes? (Logische Bedingung.)
125. Vergleiche das Phänomen des Denkens mit dem Phänomen des Brennens! Kann nicht das Brennen, die Flamme uns rätselhaft erscheinen? Und warum die Flamme mehr als der Tisch?——Und wie klärst du dieses Rätsel auf?
Und wie soll nun das Rätsel des Denkens aufgelöst werden?—Wie das der Flamme?
126. Ist die Flamme nicht rätselhaft, weil sie ungreifbar ist? Wohl—aber warum macht sie das rätselhaft? Warum soll das Ungreifbare rätselhafter sein, als das Greifbare? Außer, weil wir es greifen wollen.—
127. Man sagt, die Seele verläßt den Körper. Um ihr dann aber jede Ähnlichkeit mit dem Körper zu nehmen, und damit man beileibe nicht denkt, es sei irgend ein gasförmiges Ding gemeint, sagt man, die Seele ist unkörperlich, unräumlich; aber mit dem Worte "verläßt" hat man schon alles gesagt. Zeige mir, wie du das Wort "seelisch" gebrauchst, und ich werde sehen, ob die Seele "unkörperlich" ist, und was du unter "Geist" verstehst.
128. Ich bin geneigt, vom Leblosen zu reden als von einem, dem etwas abgeht. Ich sehe das Leben unbedingt als ein Plus an, als etwas dem Leblosen Hinzugefügtes. (Psychologische Atmosphäre.)
129. Man sagt vom Tisch und Stuhl nicht: "er denkt jetzt", noch "er denkt jetzt nicht", noch "er denkt nie"; auch von der Pflanze nicht, auch vom Fisch nicht, kaum vom Hund; aber vom Menschen. Und auch nicht von allen Menschen.
"Ein Tisch denkt nicht" ist nicht vergleichbar einer Aussage wie "ein Tisch wächst nicht". (Ich wüßte gar nicht, wie das wäre, wenn ein Tisch dächte.) Und hier gibt es offenbar einen graduellen Übergang zu dem Fall des Menschen.
130. Man redet nur vom 'Denken' unter ganz bestimmten Umständen.
131. Wie können denn der Sinn und die Wahrheit (oder die Wahrheit und der Sinn) der Sätze zugleich zusammenbrechen? (Mit einander stehen und fallen?)
132. Und ist es nicht, als wolltest du sagen: "Wenn es sich nicht so und so verhält, hat es keinen Sinn mehr zu sagen, es verhalte sich so"?
133. Also z. B.: "Wenn immer falsch gezogen worden wäre, so hätte es keinen Sinn, von einem 'falschen Zug' zu reden." Aber das ist nur eine paradoxe Form, es zu sagen. Die nicht-paradoxe Form wäre: "Die allgemeine Beschreibung ..... hat keinen Sinn."
134. Statt "man kann nicht", sage: "es gibt in diesem Spiel nicht". Statt "man kann im Damespiel nicht rochieren"—"es gibt im Damespiel kein Rochieren"; statt "ich kann meine Empfindung nicht vorzeigen"—"es gibt in der Verwendung des Wortes 'Empfindung' kein Vorzeigen dessen, was man har"; statt "man kann nicht alle Kardinalzahlen aufzählen"—"es gibt hier kein Aufzählen aller Glieder".
135. Das Gespräch, die Anwendung und Ausdeutung der Worte fließt dahin, und nur im Fluß hat das Wort seine Bedeutung.
"Er ist abgereist."—"Warum?"—Was meintest du, als du das Wort "warum" aussprachst? Woran dachtest du?
136. Denk ans Aufzeigen in der Schule. Muß einer sich die Antwort im Stillen vorgesagt haben, um mit Recht aufzeigen zu können? Und was muß in ihm dazu vorgegangen sein?—Nichts. Aber es ist wichtig, daß er für gewöhnlich eine Antwort wisse, wenn er aufzeigt; und das ist das Kriterium dafür, daß er das Aufzeigen versteht.
Es muß nichts in ihm vorgegangen sein; und doch wäre der merkwürdig, der in so einem Falle nie etwas über innere Vorgänge zu berichten wüßte.
137. Manchmal, wenn ich sage "Ich dachte damals .....", kann ich berichten, daß ich mir eben diese Worte laut oder im Stillen gesagt hatte; oder wenn nicht diese, so andere Worte, wovon die gegenwärtigen eine sinngemäße Wiedergabe sind. Das kommt doch manchmal vor! Aber eben auch dies, daß meine gegenwärtigen Worte 'nicht eine Wiedergabe' sind. Denn 'Wiedergabe' sind sie nur, wenn sie es nach Regeln der Abbildung sind.
138. Es scheint so, als wäre in einem Satz, der z. B. das Wort "Kugel" enthält, schon der Schatten anderer Verwendungen dieses Worts enthalten. Nämlich eben die Möglichkeit, jene andern Sätze zu bilden.—Wem scheint es so? und unter welchen Umständen?
139. Man kommt nicht davon weg, daß der Sinn des Satzes den Satz begleitet; bei dem Satz steht.
140. Man will etwa sagen: "Die eine Verneinung tut dasselbe mit dem Satz, wie die andere, sie schließt, was er beschreibt, aus." Aber das sind nur andere Worte für eine Gleichsetzung der beiden negativen Sätze (welche nur gilt, wenn der verneinte Satz nicht selbst ein negativer Satz ist). Immer wieder der Gedanke, daß, was wir vom Zeichen sehen, nur eine Außenseite zu einem Innern ist, worin sich die eigentlichen Operationen des Sinnes und der Bedeutung abspielen.
141. Unser Problem könnte man (sehr klar) so stellen: Angenommen, wir hätten zwei Systeme der Längenmessung: eine Länge wird in beiden durch ein Zahlzeichen ausgedrückt, diesem folgt ein Wort, das das Maß angibt. Das eine System bezeichnet eine Länge als "n Fuß", und Fuß ist eine Längeneinheit im gewöhnlichen Sinne; im andern System wird eine Länge mit "n W" bezeichnet und 1 Fuß = 1 W. Aber 2 W = 4 Fuß, 3 W = 9 Fuß u.s.w.—Also heißt der Satz "Dieser Stock ist 1 W lang" dasselbe wie "Dieser Stock ist 1 Fuß lang". Frage: Hat in diesen beiden Sätzen "W" und "Fuß" dieselbe Bedeutung?
142. Die Frage ist falsch gestellt. Das sieht man, wenn wir die Bedeutungsgleichheit durch eine Gleichung ausdrücken. Die Frage kann nur lauten: "Ist W = Fuß oder nicht?"—Von den Sätzen, in denen diese Zeichen stehen, ist hier nicht die Rede.—Ebenso wenig kann man natürlich in dieser Terminologie fragen, ob "ist" hier das Gleiche bedeutet, wie "ist" dort; wohl aber, ob die Kopula das Gleiche bedeutet, wie das Gleichheitszeichen. Nun, wir sagten ja: 1 Fuß = 1 W; aber Fuß ≠ W.
143. Man könnte sagen: in allen Fällen meint man mit "Gedanke" das Lebende am Satz. Das, ohne welches er tot, eine bloße Lautfolge oder Folge geschriebener Figuren ist.
Wenn ich aber ebenso von einem Etwas spräche, welches einer Konfiguration von Schachfiguren Bedeutung gibt, d. h., sie von einer beliebigen Zusammenstellung von Holzklötzchen unterscheidet,—was könnte ich da nicht alles meinen? Die Regeln, die die Schachkonfiguration zu einer Situation eines Spiels machen; die besondern Erlebnisse, die wir mit solchen Spielstellungen verbinden; den Nutzen des Spiels.
Oder wenn wir von einem Etwas sprachen, welches das Papiergeld von bloßen bedruckten Zetteln unterscheidet und ihm seine Bedeutung, sein Leben gibt!
144. Wie ein Wort verstanden wird, das sagen Worte allein nicht. (Theologie.)
145. Es könnte auch eine Sprache geben, in deren Verwendung der Eindruck, den wir von den Zeichen erhalten, keine Rolle spielt; in der es ein Verstehen im Sinne eines solchen Eindrucks nicht gibt. Die Zeichen werden uns etwa geschrieben übermittelt, und wir können sie uns nun merken. (D. h. der einzige Eindruck, von dem da die Rede ist, ist das Bild des Zeichens.) Wenn es nun ein Befehl ist, so übertragen wir nach Regeln, Tabellen, das Zeichen in Handlung. Zum Eindruck, ähnlich dem eines Bildes, kommt es nicht und man schreibt auch nicht Geschichten in dieser Sprache.
146. In diesem Fall könnte man sagen: "Das Zeichen lebt nur im System."
147. Es wäre natürlich auch denkbar, daß wir einen Satz der Wortsprache, um von ihm einen Eindruck zu erhalten, nach Regeln in ein gezeichnetes Bild übertragen müßten. (Daß erst dies Bild eine Seele hätte.)
148. Es wäre eine Sprache denkbar, in der die Bedeutungen von Worten nach bestimmten Regeln abwechselten, etwa: Vormittag heißt das Wort A dies, Nachmittag jenes.
Oder eine Sprache, in der die Wörter sich täglich änderten, indem an jedem Tag jeder Buchstabe des vorigen Tages durch den nächsten im Alphabet (und z durch a) ersetzt würde.
149. Denke dir diese Sprache: Wörter und Grammatik sind die des Deutschen, aber die Wörter im Satz stehen in der entgegengesetzten Reihenfolge. Ein Satz dieser Sprache klingt also wie ein deutscher Satz, den man vom Schlußpunkt zum Anfang hin liest. Die Ausdrucksmöglichkeiten haben also die gleiche Mannigfaltigkeit, wie im Deutschen. Aber was wir als Satzklang kennen, ist vernichtet.
150. Jemand, der nicht Deutsch kann, hört mich bei gewissen Anlässen ausrufen: "Welch herrliche Beleuchtung!" Er errät den Sinn und gebraucht nun den Ausruf selber, wie ich es tue, ohne jedoch die drei Wörter zu verstehen. Versteht er den Ausruf?
151. Ich hatte mit Absicht ein Beispiel gewählt, in dem der Mensch einer Empfindung Ausdruck gibt. Denn in diesem Fall sagt man, Laute, die keiner Sprache angehören, seien voll von Bedeutung.
152. Wäre es ebenso leicht, sich den analogen Fall zu denken für diesen Satz: "Wenn der Zug nicht pünktlich um s Uhr ankommt, wird er den Anschluß versäumen"? Was hiebe es etwa in diesem Falle: den Sinn erraten?
153. Es stört uns gleichsam, daß der Gedanke eines Satzes in keinem Moment ganz vorhanden ist. Wir sehen ihn wie einen Gegenstand an, den wir erzeugen und nie ganz besitzen, denn kaum entsteht ein Teil, so verschwindet ein anderer.
154. (Zu No. 150) Man kann sich leicht eine Sprache vorstellen, in der Menschen ein einziges Wort für jenen Ausruf benutzen. Aber wie wäre es mit einem Wort für den Satz "Wenn der Zug ...."? In was für einem Fall würden wir sagen, daß das Wort tatsächlich für diesen Satz steht?
Etwa in diesem: Die Leute benützten anfänglich einen Satz, wie den unsern; dann aber träten Umstände ein, in denen der Satz so häufig ausgesprochen werden müßte, daß sie ihn zu einem Wort zusammenzogen. Diese Leute könnten also noch das Wort durch den Satz erklären.
Aber kann es auch den Fall geben, in dem Leute nur ein Wort für jenen Sinn besäßen, also für jenen Gebrauch? Warum nicht? Man muß sich vorstellen, wie einer den Gebrauch dieses Wortes lernt, und unter welchen Umständen wir sagen würden, daß das Wort wirklich jenen Satz vertritt.
Bedenk aber dies: In unserer Sprache sagt jemand "Er kommt um 5 Uhr an"; ein Andrer antwortet "Nein, 10 Minuten nach 5". Gibt es diese Art Gespräch auch in der andern Sprache?
Darum sind Sinn und Bedeutung vage Begriffe.
155. Worte eines Dichters können uns durch und durch gehen. Und das hängt kausal natürlich mit dem Gebrauch zusammen, den sie in unserm Leben haben. Und es hängt auch damit zusammen, daß wir, diesem Gebrauch gemäß, unsere Gedanken dorthin und dahin in die wohlbekannte Umgebung der Worte schweifen lassen.
156. Gibt es einen Unterschied der Bedeutung, der sich erklären läßt und einen, der in einer Erklärung nicht zu Tage tritt?
157. Der seelenvolle Ausdruck in der Musik,—er ist doch nicht nach Regeln zu erkennen. Und warum können wir uns nicht vorstellen, daß er's für andere Wesen wäre?
158. Wenn dir plötzlich ein Thema, eine Wendung etwas sagt, so brauchst du dir's nicht erklären zu können. Es ist dir plötzlich auch diese Geste zugänglich.
159. Du redest doch vom Verstehen der Musik. Du verstehst sie doch, während du sie hörst! Sollen wir davon sagen, es sei ein Erlebnis, welches das Hören begleite?
160. Das Sprechen der Musik. Vergiß nicht, daß ein Gedicht, wenn auch in der Sprache der Mitteilung abgefaßt, nicht im Sprachspiel der Mitteilung verwendet wird.
161. Könnte man sich nicht denken, daß einer, der Musik nie gekannt hat und zu uns kommt und jemanden einen nachdenklichen Chopin spielen hört, daß der überzeugt wäre, dies sei eine Sprache, und man wolle ihm nur den Sinn geheimhalten.
In der Wortsprache ist ein starkes musikalisches Element. (Ein Seufzer, der Tonfall der Frage, der Verkündigung, der Sehnsucht, alle die unzähligen Gesten des Tonfalls.)
162. Wenn ich aber eine Melodie mit Verständnis höre, geht da nicht etwas Besonderes in mir vor—was nicht vorgeht, wenn ich sie verständnislos höre? Und was?—Es kommt keine Antwort; oder was mir einfällt, ist abgeschmackt. Ich kann wohl sagen: "Jetzt habe ich sie verstanden" und nun etwa über sie reden, sie spielen, sie mit andern vergleichen etc. Zeichen des Verständnisses mögen das Hören begleiten.
163. Es ist falsch, das Verstehen einen Vorgang zu nennen, der das Hören begleitet. (Man könnte ja auch die Äußerung davon, das ausdrucksvolle Spiel, nicht eine Begleitung des Hörens nennen.)
164. Denn wie läßt sich erklären, was 'ausdrucksvolles Spiel' ist? Gewiß nicht durch etwas, was das Spiel begleitet.—Was gehört also dazu? Eine Kultur, möchte man sagen.—Wer in einer bestimmten Kultur erzogen ist,—dann auf Musik so und so reagiert, dem wird man den Gebrauch des Wortes "ausdrucksvolles Spiel" beibringen können.
165. Das Verstehen der Musik ist weder eine Empfindung, noch eine Summe von Empfindungen. Es ein Erlebnis zu nennen, ist aber dennoch insofern richtig, als dieser Begriff des Verstehens manche Verwandtschaften mit andern Erlebnisbegriffen hat. Man sagt "Ich habe diese Stelle diesmal ganz anders erlebt". Aber doch sagt dieser Ausdruck 'was geschah' nur für den, der in einer besonderen, diesen Situationen angehörigen Begriffswelt zu Hause ist. (Analogie: "Ich habe die Partie gewonnen".)
166. Beim Lesen schwebt mir das vor. So geht also etwas beim Lesen vor sich ....?—Diese Frage führt ja nicht weiter.
167. Wie kann mir doch das vorschweben?—Nicht in den Dimensionen, an die du denkst.
168. Wie weiß ich, daß einer entzückt ist? Wie lernt man den sprachlichen Ausdruck des Entzückens? Woran knüpft er sich? An den Ausdruck von Körperempfindungen? Fragen wir einen, was er in der Brust, in den Gesichtsmuskeln spürt um herauszufinden, ob er Genuß empfindet?
169. Heißt das aber, es gäbe nicht Empfindungen, die oft beim Genießen der Musik wiederkehren? Durchaus nicht.
170. Ein Gedicht macht uns beim Lesen einen Eindruck. "Fühlst du dasselbe, während du es liest, wie wenn du etwas Gleichgültiges liest?"—Wie habe ich auf diese Frage antworten gelernt? Ich werde vielleicht sagen: "Natürlich nicht!"—was soviel heißt, wie: mich ergreift dies, und das Andere nicht.
"Ich erlebe dabei etwas Anderes."—Und welcher Art ist dies?—Ich kann nichts Befriedigendes antworten. Denn, was ich angebe, ist nicht das Wichtigste.—"Hast du aber nicht während des Lesens genossen?" Freilich——denn die entgegengesetzte Antwort hieße: ich hätte es früher oder später genossen, und das will ich nicht sagen.
Aber nun erinnerst du dich ja doch an Empfindungen und Vorstellungen beim Lesen und zwar solche, die mit dem Genießen, mit dem Eindruck zusammenhängen.—Aber die hatten ihre Bedeutsamkeit nur durch ihre Umgebung erhalten: durch das Lesen des Gedichts, durch meine Vertrautheit mit der Sprache, dem Metrum und unzähligen Zusammenhangen.
Du mußt dich doch fragen, wie haben wir den Ausdruck "Ist das nicht herrlich!" überhaupt gelernt?—Niemand erklärte ihn uns, indem er sich auf Empfindungen, Vorstellungen oder Gedanken bezog, die das Hören begleiten! Ja, wir würden nicht bezweifeln, daß er's genossen hat, wenn er keine solchen Erlebnisse anzugeben wüßte; wohl aber, wenn es sich zeigte, daß er gewisse Zusammenhänge nicht versteht.
171. Aber zeigt sich das Verständnis nicht z. B. darin, mit welchem Ausdruck einer das Gedicht liest, die Melodie singt? Gewiß. Aber was ist nun hier das Erlebnis während des Lesens? Da müßte man ja sagen: der genieße und verstehe es, der es gut gelesen hört oder in den Sprechorganen fühlt.
172. Man kann auch vom Verstehen einer musikalischen Phrase sagen, es sei das Verstehen einer Sprache.
173. Ich denke an eine ganz kurze von nur zwei Takten. Du sagst "Was liegt nicht alles in ihr!" Aber es ist nur sozusagen eine optische Täuschung, wenn du denkst, beim Hören gehe vor, was in ihr liegt. ("Es kommt drauf an, wer's sagt".) (Nur in dem Fluß der Gedanken und des Lebens haben die Worte Bedeutung.)
174. Nicht das enthält die Täuschung: "Jetzt habe ich's verstanden"—und nun folgt vielleicht eine lange Erklärung dessen, was ich verstanden habe.
175. Weist das Thema auf nichts außer sich? Oh ja! Das heißt aber:—Der Eindruck, den es mir macht, hängt mit Dingen in seiner Umgebung zusammen—z. B. mit unserer Sprache und ihrer Intonation, also mit dem ganzen Feld unserer Sprachspiele.
Wenn ich z. B. sage: Es ist, als ob hier ein Schluß gezogen würde oder, als ob hier etwas bekräftigt würde oder, als ob dies eine Antwort auf das Frühere wäre,—so setzt mein Verständnis eben die Vertrautheit mit Schlüssen, Bekräftigungen, Antworten voraus.
176. Die Worte "Gottlob! Noch etwas Weniges hat man geflüchtet—vor den Fingern der Kroaten", mit ihrem Ton und Blick, scheinen allerdings schon jede Nuance ihrer Bedeutung in sich zu tragen. Nur darum aber, weil wir sie als Teil einer bestimmten Szene kennen. Man könnte aber eine ganz andere Szene um diese Worte (im gleichen Tone gesprochen) bauen um zu zeigen, wie ihre besondere Seele in der Geschichte liegt, zu der sie gehören.
177. Wenn ich einen mit verbannender Gebärde sagen höre "Weiche!", erlebe ich hier die Bedeutung des Wortes, wie in dem Spiel, wenn ich mir's für mich vorsage und es einmal so und einmal so 'meine?—Denn er konnte ja auch sagen "Weiche von mir", und dann erlebte ich vielleicht die ganze Phrase so und so; aber auch das einzelne Wort? Die ergänzenden Worte waren es vielleicht, die mir den Eindruck machten.
178. Das besondere Erlebnis der Bedeutung ist charakterisiert dadurch, daß wir mit einer Erklärung und der Vergangenheitsform reagieren: gerade so, als erklärten wir die Bedeutung eines Worts für praktische Zwecke.
179. Vergiß, vergiß, daß du diese Erlebnisse selber hast!
180. Wie konnte er das Wort in der Bedeutung hören? Wie war es möglich?! Gar nicht——in diesen Dimensionen.——
181. Aber ist es also nicht wahr, daß das Wort für mich jetzt das bedeutet? Warum nicht? Es kommt ja dieser Sinn mit der übrigen Verwendung des Wortes nicht in Konflikt.
Es sagt einer: "Gib ihm die Nachricht .... und meine damit ....!"——Was wäre der Sinn dieses Befehls?
182. "Als ich das Wort jetzt aussprach, bedeutete es für mich....". Warum sollte das nicht einfach Wahnsinn sein? Weil ich das erlebte? Das ist kein Grund.
183. Der, den ich bedeutungsblind nenne, wird wohl den Auftrag verstehen: "Sag ihm, er solle zur Bank gehen,—ich meine die Gartenbank", aber nicht: "Sag das Wort Bank und meine damit Gartenbank". Welche Formen geistiger Defekte bei Menschen vorgefunden werden, kümmert diese Untersuchung nicht; wohl aber die Möglichkeit solcher Formen. Nicht, ob es Menschen gibt, die eines Gedankens vom Typus "Ich wollte damals ...." nicht fähig sind,—sondern wie der Begriff so eines Defekts durchzuführen wäre, interessiert uns.
Wenn du annimmst, daß einer das nicht kann, wie ist es dann mit dem? Soll er es auch nicht können?—Wohin führt uns dieser Begriff? Denn wir haben ja hier Paradigmen.
184. Verschiedene Menschen empfinden es sehr verschieden stark, wenn die Rechtschreibung eines Worts geändert wird. Und die Empfindung ist nicht nur Pietät für einen alten Gebrauch.—Wem die Orthographie nur eine praktische Frage ist, dem geht ein Gefühl ab, nicht unähnlich dem, welches einem "Bedeutungsblinden" mangeln würde. (Goethe über Personennamen. Die Nummer des Gefangenen.)
185. Wie mancher auch die Frage nicht versteht "Welche Farbe hat für dich der Vokal a?"—Wenn einer sie nicht verstünde, wenn er erklärte, sie sei Unsinn,—könnten wir sagen, er verstehe nicht deutsch, oder nicht die Bedeutungen der Wörter "Farbe", "Vokal", etc.?
Im Gegenteil: Wenn er diese Worte verstehen gelernt hat, dann kann er auch auf jene Fragen 'mit Verständnis' oder 'ohne Verständnis' reagieren.
186. Mißverständnis—Unverständnis. Verständnis wird durch Erklärung bewirkt; aber auch durch Abrichtung.
187. Warum kann man einer Katze nicht das Apportieren beibringen? Versteht sie nicht, was man will? Und worin besteht hier Verstehen und Unverständnis ?
188. "Ich lese jedes Wort mit dem ihm entsprechenden Gefühl. Das Wort aber z. B. mit dem Abergefühl—u.s.w."——Und selbst wenn das wahr ist,—was bedeutet es eigentlich? Was ist die Logik des Begriffs 'Abergefühl'?—Es wird ja nicht ein Gefühl dadurch, daß ich es "Gefühl" nenne.
189. Ist Lügen ein bestimmtes Erlebnis? Nun, kann ich denn jemandem sagen "Ich werde dich jetzt anlügen" und es dann tun?
190. Inwiefern ist mir die Lüge bewußt, während ich lüge? Nur insofern, als sie mir nicht später erst zum Bewußtsein kommt, und ich doch später weiß, daß ich gelogen habe. Das Sich-der-Lüge-bewußt-sein ist ein Können. Dem widerspricht nicht, daß es charakteristische Gefühle des Lügens gibt. [Randbemerkung: Absicht.]
191. Das Wissen wird eben nicht in Worte übersetzt, wenn es sich äußert. Die Worte sind keine Übersetzung eines Andern, welches vor ihnen da war,
192. "Sich etwas vornehmen, ist ein besonderer innerer Vorgang."—Aber was für ein Vorgang—auch wenn du ihn erdichten dürftest—könnte denn das leisten, was wir vom Vorsatz fordern?
193. Ist es nicht genau so mit dem Verbum "verstehen"? Es erklärt mir jemand die Route, die ich dort und dorthin zu nehmen habe. Er fragt "Hast du mich verstanden?" Ich antworte "Ich hab's verstanden."—Will ich ihm mitteilen, was in mir während seiner Erklärung vorging?—Und doch liebe sich auch das mitteilen.
194. Denk dir dieses Spiel: Eine Liste von Wörtern verschiedener Sprachen und von sinnlosen Lautreihen wird mir vorgelesen. Ich soll nach jedem sagen, ob ich es verstehe oder nicht; auch, was beim Verstehen oder Nichtverstehen in mir vorging.—Auf das Wort "Baum" werde ich, ohne mich zu bedenken, mit "ja" antworten (ein Bild mag mir dabei vorschweben); auf eine Lautzusammenstellung, die ich noch nie gehört habe, antworte ich ebenso unbedenklich mit "nein". Bei Wörtern, die einen speziellen Farbton bezeichnen, wird häufig ein Vorstellen der Antwort vorhergehen; bei seltenen Wörtern ("Kontinuum" etwa) ein Überlegen; bei Wörtern, wie der Artikel "das" etwa ein Achselzucken; Wörter einer fremden Sprache werde ich manchmal ins Deutsche Übersetzen; schweben mir Bilder vor, so sind es manchmal die der Gegenstände, die von den Worten bezeichnet werden (wieder tausenderlei Fälle), manchmal andere Bilder.
Dies Spiel könnte man durch eines ergänzen, in welchem einer die Namen von Tätigkeiten nennt und bei jeder fragt: "Kannst du das?"—Das Subjekt soll angeben, welche Gründe es hatte, die Frage mit "ja" oder "nein" zu beantworten.
195. Denken wir uns eine Art Vexierbild, worin nicht ein bestimmter Gegenstand aufzufinden ist, sondern das uns auf den ersten Blick als ein Gewirr nichtssagender Striche erscheint und nach einigem Suchen erst als, sagen wir, ein Landschaftsbild.—Worin besteht der Unterschied zwischen dem Anblick des Bildes vor und nach der Lösung? Daß wir es beide Male anders sehen, ist klar. In wiefern aber kann man nach der Auflösung sagen, jetzt sage uns das Bild etwas, früher habe es uns nichts gesagt?
196. Wir können diese Frage auch so stellen: Was ist das allgemeine Charakteristikum dafür, daß die Lösung gefunden ist?
197. Ich will annehmen, daß ich, sobald es gelöst ist, die Lösung dadurch kenntlich mache, daß ich gewisse Striche des Bildes stark nachziehe und etwa Schatten eintrage. Warum nennst du nun das Bild, was du eingezeichnet hast, eine Auflösung?
- (a) Weil es die klare Darstellung einer Gruppe räumlicher Gegenstände ist.
- (b) Weil es die Darstellung eines regelmäßigen Körpers ist.
- (c) Weil es eine symmetrische Figur ist.
- (d) Weil es eine Figur ist, die mir einen ornamentalen Eindruck macht.
- (e) Weil es die Darstellung eines Körpers ist, der mir bekannt vorkommt.
- (f) Weil es eine Liste von Auflösungen gibt und diese Figur (dieser Körper) auf der Liste steht.
- (g) Weil es eine Art von Gegenstand darstellt, die ich wohl kenne: denn er macht mir den augenblicklichen Eindruck der Wohlbekanntheit, ich verbinde augenblicklich alle möglichen Assoziationen mit ihm; ich weiß, wie er heißt; ich weiß, daß ich ihn oft gesehen habe; ich weiß, wozu man ihn gebraucht; etc.
- (h) Weil ich den Gegenstand wohl zu kennen scheine: es fällt mir sogleich ein Wort als sein Name ein (obwohl das Wort keiner bestehenden Sprache angehört); ich sage mir "Natürlich, das ist ja ein ....." und gebe mir eine unsinnige Erklärung, die mir in diesem Augenblick sinnvoll erscheint. (Wie im Traum.)
- (i) Weil es ein Gesicht darstellt, welches mir bekannt vorkommt.
- (j) Weil es ein Gesicht darstellt, welches ich erkenne: es ist das Gesicht meines Freundes N; es ist ein Gesicht, welches ich oft abgebildet gesehen habe. Etc.
- (k) Weil es einen Gegenstand darstellt, den ich mich erinnere, einmal gesehen zu haben.
- (l) Weil es ein Ornament ist, das ich gut kenne (obwohl ich nicht weiß, wo ich es gesehen habe).
- (m) Weil es ein Ornament ist, das ich gut kenne: ich kenne seinen Namen, weiß, wo ich es schon gesehen habe.
- (n) Weil es einen Einrichtungsgegenstand meines Zimmers darstellt.
- (o) Weil ich instinktiv diese Striche nachgezogen habe und mich nun beruhigt fühle.
- (p) Weil ich mich erinnere, daß dieser Gegenstand beschrieben worden ist.
U. s. w.
(Wer nicht versteht, warum wir über diese Dinge reden, muß, was wir sagen, als leere Spielerei empfinden.)
198. Kann ich mir den Eindruck der Bekanntschaft wegdenken, wo er ist; und hinzudenken, wo er nicht ist? Und was heißt das? Ich sehe z. B. das Gesicht eines Freundes an und frage mich: Wie schaut dieses Gesicht aus, wenn ich es als ein mir fremdes Gesicht sehe (als sähe ich es etwa jetzt zum erstenmal)? Was bleibt sozusagen von dem Anblick des Gesichts, wenn ich den Eindruck der Bekanntheit wegdenke, abziehe? Hier bin ich nun geneigt zu sagen: "Es ist sehr schwer, die Bekanntheit von dem Eindruck des Gesichts zu trennen." Aber ich fühle auch, daß das eine schlechte Ausdrucksweise ist. Ich weiß nämlich gar nicht, wie ich es auch nur versuchen soll, diese beiden zu trennen. Der Ausdruck "sie trennen" hat für mich gar keinen klaren Sinn.
Ich weiß, was es heißt: "Stell dir diesen Tisch schwarz vor statt braun." Dem entspricht: "Male diesen Tisch, aber schwarz statt braun".
199. Wie, wenn man sagte: "Denke dir diesen Schmetterling genau so wie er ist, aber häßlich statt schön"?!
200. Wir haben in diesem Fall nicht bestimmt, was es heißen soll, sich die Wohlbekanntheit wegzudenken.
Es könnte etwa heißen, sich des Eindrucks entsinnen, den ich hatte, als ich das Gesicht zum ersten Male sah.
201. Die zeichnerische Darstellung des Innern eines Radio empfängers wird für den, der keine Kunde von solchen Dingen hat, Gewirr sinnloser Striche sein. Hat er aber den Apparat und seine Funktion kennengelernt, so wird jene Zeichnung für ihn ein sinnvolles Bild sein.
Gegeben nun irgend eine mir jetzt sinnlose körperliche Gestalt (etwa im Bild)—kann ich nach Belieben sie sinnvoll vorstellen? Das wäre, als fragte man: Kann ich mir einen beliebig geformten Gegenstand als Gebrauchsgegenstand vorstellen? Aber für welchen Gebrauch?
Man könnte eine Klasse von Körperformen sich methodisch als Wohnungen von Tieren oder Menschen denken. Eine andere Klasse als Waffen. Eine etwa als Modelle von Landschaften. Etc. etc. Und hier weiß ich also, wie ich einer sinnlosen Form Sinn andichten kann.
202. Überlege wohl, wie wir das Wort "erkennen" benützen! Ich erkenne die Möbel in meinem Zimmer, meinen Freund, den ich täglich sehe. Aber kein 'Wiedererkennen spielt sich ab'.
203. Man könnte sagen: Ich hätte keinen Eindruck von dem Zimmer als Ganzes, könnte ich nicht meinen Blick schnell in ihm dahin und dorthin schweifen lassen und mich nicht frei in ihm herumbewegen. (Stream of thought.) Aber nun ist die Frage, wie manifestiert es sich, daß ich 'von ihm als Ganzes einen Eindruck habe'? Z. B. in der Selbstverständlichkeit, mit der ich mich in ihm zurechtfinde; in der Abwesenheit des Suchens, Zweifelns und der Verwunderung. Darin, daß eine Unzahl von Tätigkeiten durch seine Wände begrenzt sind, und daß ich alles das als "mein Zimmer" in der Rede zusammenfasse. Darin, daß ich es nützlich und notwendig finde, mich immer wieder des Begriffs 'mein Zimmer' zu bedienen im Gegensatz zu seinen Wänden, Ecken, etc.
204. Wie sieht die Beschreibung einer 'Einstellung' aus?
Man sagt z. B.: "Sieh von diesen Flecken ab und auch von dieser kleinen Unregelmäßigkeit, und schau es als Bild eines .... an!"
"Denk dir das weg! Wär's dir auch ohne dieses .... unangenehm?" Man wird doch sagen, ich ändere mein Gesichtsbild—wie durch Blinzeln oder Weghalten eines Details. Dieses "Absehen von ..." spielt doch eine ganz ähnliche Rolle, wie etwa die Anfertigung eines neuen Bildes.
205. Nun wohl,—und das sind gute Gründe dafür zu sagen, wir hätten durch unsre Einstellung unsern Gesichtseindruck geändert. D. h., es sind (dies) gute Gründe, den Begriff 'Gesichtseindruck' so zu begrenzen.
206. "Aber ich kann doch offenbar im Sehen Elemente (Striche z. B.) zusammennehmen!" Aber warum nennt man es "zusammennehmen"? Warum braucht man hier ein Wort—wesentlich—das schon eine andere Bedeutung hat? (Es ist hier natürlich wie im Fall des Wortes "Kopfrechnen".)
207. Wenn ich jemandem sage: "Nimm diese Striche (oder anderes) zusammen!" was wird er tun? Nun, Verschiedenes, je nach den Umständen. Vielleicht soll er sie zu zwei und zwei zählen oder in eine Lade legen oder anblicken etc.
208. Überlegen wir uns, was man über ein Phänomen, wie dieses, sagt:
Die Figur ![]() einmal als ein F, einmal als das Spiegelbild eines F sehen.
einmal als ein F, einmal als das Spiegelbild eines F sehen.
Ich will fragen: Worin besteht es, die Figur einmal so, einmal anders sehen?—Sehe ich wirklich jedesmal etwas Anderes? Oder deute ich nur, was ich sehe, auf verschiedene Weise?—Ich bin geneigt, das erste zu sagen. Aber warum? Nun, Deuten ist eine Handlung. Es kann z. B. darin bestehen, daß einer sagt "Das soll ein F sein"; oder daß er's nicht sagt, aber das Zeichen beim Kopieren durch ein F ersetzt; oder sich überlegt: "Was mag das wohl sein? Es wird ein F sein, das dem Schreiber mißglückt ist."—Sehen ist keine Handlung, sondern ein Zustand. (Grammatische Bemerkung.) Und wenn ich die Figur nie anders als F gelesen, mir nie überlegt habe, was es wohl sein mag, so wird man sagen, ich sehe sie als F; wenn man nämlich weiß, daß es sich auch anders sehen läßt. "Deuten" würde ich es nennen, wenn ich sagte: "Das soll gewiß ein F sein; der Schreiber schreibt alle seine F so."
Wie ist man denn überhaupt zu dem Begriff des 'Dies als das kommen? Bei welchen Gelegenheiten wird er gebildet, ist für ihn ein Bedarf? (Sehr häufig in der Kunst.) Dort z. B., wo es sich um ein Phrasieren durchs Auge oder Ohr handelt. Wir sagen "Du mußt diese Takte als Einleitung hören", "Du mußt nach dieser Tonart hin hören", "Wenn man diese Figur einmal als .... gesehen hat, ist es schwer, sie anders zu sehen", "Ich höre das französische 'ne .... pas' als zweiteilige Verneinung, aber nicht als 'nicht ein Schritt'", etc. etc. Ist es nun ein wirkliches Sehen oder Hören? Nun: so nennen wir es; mit diesen Worten reagieren wir in bestimmten Situationen. Und auf diese Worte reagieren wir wieder durch bestimmte Handlungen.
209. Diese Form, die ich sehe—möchte ich sagen—ist nicht einfach eine Form, sondern sie ist eine von den mir bekannten Formen; sie ist eine im Vorhinein ausgezeichnete Form. Sie ist eine von den Formen, deren Bild schon früher in mir war, und nur weil sie so einem Bild entspricht, ist sie die wohlbekannte Form. (Ich trage gleichsam einen Katalog solcher Formen mit mir herum und die Gegenstände, die dort abgebildet sind, sind dann die wohlbekannten.)
210. Aber daß ich das Bild schon früher mit mir herumgetragen habe, wäre nur eine kausale Erklärung des gegenwärtigen Eindrucks. Es ist, als sagte man: diese Bewegung geht so leicht, als wäre sie eingeübt worden.
211. "Wenn ich gefragt werde 'Siehst du dort eine Kugel?, ein andermal 'Siehst du dort die Halbkugel?', so kann, was ich sehe, beide Male das Gleiche sein, und wenn ich antworte 'Ja', so unterscheide ich doch zwischen den beiden Hypothesen. Wie ich im Schachspiel zwischen einem Bauern und dem König unterscheide, auch wenn der gegenwärtige Zug einer ist, den beide machen könnten, und wenn selbst eine Königsfigur als Bauer fungierte."—Man ist in der Philosophie immer in Gefahr, einen Mythus des Symbolismus zu erzeugen, oder einen der seelischen Vorgänge. Statt einfach zu sagen, was jeder weiß und zugeben muß.
212. Ist es Introspektion, was mich lehrt, ob ich's mit einem echten Sehen zu tun habe, oder doch mit einem Deuten? Zuerst einmal muß ich mir klar werden, was ich denn ein Deuten nennen würde; woran sich erkennen läßt, ob etwas ein Deuten oder ein Sehen zu nennen ist. [Randbemerkung: Einer Deutung entsprechend sehen.]
213. Sehe ich die Figur nicht einmal so, einmal anders, auch wenn ich nicht mit Worten oder sonst wie reagiere?
Aber "einmal so", "einmal anders" sind ja Worte, und mit welchem Recht gebrauche ich sie hier? Kann ich dir oder mir selbst mein Recht erweisen? (Es sei denn durch eine weitere Reaktion.)
Aber ich weiß doch, daß es zwei Eindrücke sind, auch wenn ich's nicht sage! Aber wie weiß ich, daß, was ich dann sage, das ist, was ich wußte? Welche Konsequenzen folgen daraus, daß ich dies als das deute? Welche daraus, daß ich dies als das sehe?
214. Erlebnis der wirklichen Größe. Wir sehen ein Bild, das die Form eines Sessels zeigt; man sagt uns, es stelle eine Konstruktion von Hausgröße vor. Nun sehen wir sie anders.
215. Denk dir, jemand, der auf die Sonne schaut, hätte plötzlich die Empfindung, daß nicht sie sich bewegt, sondern wir an ihr vorüberziehen. Nun will er sagen, er habe einen neuen Bewegungszustand gesehen, in dem wir uns befinden; und denke, er zeigt nun durch Gebärden, welche Bewegung er meint, und daß es nicht die der Sonne ist. Wir hätten es hier mit zwei verschiedenen Anwendungen des Wortes "Bewegung" zu tun.
216. Nicht den Aspektwechsel sieht man, sondern den Deutungswechsel.
217. Du siehst es nicht einer Deutung, sondern einem Deuten gemäß.
218. Ich deute die Worte; wohl aber deute ich auch die Mienen? Deute ich einen Gesichtsausdruck als drohend oder freundlich? Es kann geschehen.
Wenn ich nun sagte: "Es ist nicht genug, daß ich das drohende Gesicht wahrnehme, sondern ich muß es erst deuten."—Es zückt jemand das Messer auf mich, und ich sage: "Ich fasse das als eine Drohung auf."
219. Chinesische Gebärden verstehen wir so wenig wie chinesische Sätze.
220. Das Bewußtsein in des Andern Gesicht. Schau ins Gesicht des Andern, und sich das Bewußtsein in ihm und einen bestimmten Bewußtseinston. Du siehst auf ihm, in ihm, Freude, Gleichgültigkeit, Interesse, Rührung, Dumpfheit u.s.f. Das Licht im Gesicht des Andern.
Schaust du in dich, um den Grimm in seinem Gesicht zu erkennen? Er ist dort so deutlich wie in deiner eigenen Brust.
(Und was will man nun sagen? Daß das Gesicht des Andern mich zur Nachahmung anregt, und daß ich also kleine Bewegungen und Muskelspannungen im eigenen empfinde und die Summe dieser meine? Unsinn. Unsinn,—denn du machst Annahmen statt bloß zu beschreiben. Wem hier Erklärungen im Kopf spuken, der vernachlässigt es, sich auf die wichtigsten Tatsachen zu besinnen.)
221. "Das Bewußtsein ist so deutlich in seinem Gesicht und Benehmen, wie in mir selbst."
222. Das menschliche Auge sehen wir nicht als Empfänger, es scheint nicht etwas einzulassen, sondern auszusenden. Das Ohr empfängt; das Auge blickt. (Es wirft Blicke, es blitzt, strahlt, leuchtet.) Mit dem Auge kann man schrecken, nicht mit dem Ohr, der Nase. Wenn du das Auge siehst, so siehst du etwas von ihm ausgehen. Du siehst den Blick des Auges.
223. "Wenn du nur von deinen physiologischen Vorurteilen wegkommst, wirst du gar nichts daran finden, daß das Blicken des Auges auch gesehen werden kann." Ich sage ja auch, ich sehe den Blick, den du dem Andern zuwirfst. Und wollte man mich verbessern und sagen, ich sähe ihn eigentlich nicht, so hielte ich das für bloße Dummheit.
Anderseits habe ich mit meiner Redeweise nicht etwas zugegeben, und ich widerspreche dem, der mir sagt, ich sähe den Blick 'geradeso' wie die Gestalt und Farbe des Auges.
Denn das 'naive Sprechen', d.h. unsere naive, normale Ausdrucksweise enthält ja keine Theorie des Sehens—zeigt dir keine Theorie, sondern nur einen Begriff des Sehens.
224. Laß einen Menschen zornig, hochmütig, ironisch blicken; und nun verhäng sein Gesicht, daß nur die Augen frei bleiben,—in denen der ganze Ausdruck vereint schien: Ihr Ausdruck ist nun überraschend vieldeutig.
225. "Man sieht Gemütsbewegung."—Im Gegensatz wozu? Man sieht nicht die Gesichtsverziehungen und schließt nun (wie der Arzt, der eine Diagnose stellt) auf Freude, Trauer, Langeweile. Man beschreibt sein Gesicht unmittelbar als traurig, glückstrahlend, gelangweilt, auch wenn man nicht imstande ist, eine andere Beschreibung der Gesichtszüge zu geben.—Die Trauer ist im Gesicht personifiziert, möchte man sagen.
Dies gehört zum Begriff der Gemütsbewegung.
226. (Die Häßlichkeit eines Menschen kann im Bild, im gemalten, abstoßen, wie in der Wirklichkeit, aber auch in der Beschreibung, in den Worten.)
227. Es ist sonderbar: Unser Verstehen einer Geste möchten wir durch ihre Übersetzung in Worte erklären, und das Verstehen von Worten durch Übersetzung in eine Geste. (So werden wir hin und her geworfen, wenn wir suchen wollen, wo das Verstehen eigentlich liegt.)
Und wirklich werden wir Worte durch eine Geste, und eine Geste durch Worte erklären.
228. Erkläre einem, die Zeigerstellung, die du aufgezeichnet hast, solle ausdrücken: die Zeiger dieser Uhr stünden jetzt so.—Die Unbeholfenheit, mit der das Zeichen, wie ein Stummer, durch allerlei suggestive Gebärden sich verständlich zu machen sucht—sie verschwindet, wenn wir erkennen, daß es aufs System ankommt, dem das Zeichen angehört.
Man wollte sagen: nur der Gedanke kann es sagen, das Zeichen nicht.
229. Eine Deutung ist doch etwas, was in Zeichen gegeben wird. Es ist diese Deutung im Gegensatz zu einer andern (die anders lautet).—Wenn man also sagen wollte "Jeder Satz bedarf noch einer Deutung", so hieße das: kein Satz kann ohne einen Zusatz verstanden werden.
230. Ähnlich wäre es fast, wenn man beim Würfeln, wieviel ein Wurf gelten soll, durch einen weitern Wurf bestimmte.
231. Mit "Intention" meine ich hier das, was das Zeichen im Gedanken verwendet. Die Intention scheint zu interpretieren, die endgültige Interpretation zu geben; aber nicht ein weiteres Zeichen oder Bild, sondern etwas Anderes, das, was man nicht wieder interpretieren kann. Aber ein psychologisches Ende ist erreicht, kein logisches.
Denken wir eine Zeichensprache, eine 'abstrakte', ich meine eine, die uns fremd ist, in der wir uns nicht heimisch fühlen, in der, wie wir sagen würden, wir nicht denken; und denken wir uns diese Sprache interpretiert durch eine Übersetzung in eine, wir wir sagen möchten, unzweideutige Bildersprache; eine Sprache, die aus perspektivisch gemalten Bildern besteht. Es ist ganz klar, daß es viel leichter ist, sich verschiedene Deutungen der Schriftzeichen zu denken, als eines in gewohnter Art gemalten Bildes. Hier werden wir auch geneigt sein zu denken, es gebe keine Möglichkeit der Deutung mehr.
232. Wir könnten da auch sagen, wir lebten nicht in der Zeichensprache, wohl aber im gemalten Bilde.
233. "Nur das intendierte Bild reicht als Maßstab an die Wirklichkeit heran. Von außen betrachtet, steht es gleich tot und isoliert da."—Es ist, als hätten wir ein Bild erst so angeschaut, daß wir in ihm leben und die Gegenstände in ihm uns als wirkliche umgeben, und dann traten wir zurück und wären nun außerhalb, sähen den Rahmen, und das Bild wäre eine bemalte Fläche. So, wenn wir intendieren, umgeben uns die Bilder der Intention, und wir leben unter ihnen. Aber wenn wir aus der Intention heraustreten, so sind es bloße Flecke auf einer Leinwand, ohne Leben und ohne Interesse für uns. Wenn wir intendieren, leben wir im Raum der Intention, unter den Bildern (Schatten) der Intention zugleich mit den wirklichen Dingen. Denken wir, wir sitzen im verdunkelten Kino und leben im Film. Der Saal wird nun erhellt, aber das Lichtspiel auf der Leinwand geht weiter. Aber jetzt stehen wir plötzlich außerhalb und sehen es als Bewegungen von lichten und dunkeln Flecken auf einer Leinwand.
(Im Traum geschieht es manchmal, daß wir eine Geschichte erst lesen und dann in ihr selbst agieren. Und nach dem Aufwachen aus einem Traum ist es manchmal, als wären wir aus dem Traum heraus zurückgetreten und sehen ihn jetzt als ein fremdes Bild vor uns.) Und es heißt auch etwas, "in den Seiten eines Buches leben".
234. Nicht das findet statt, daß sich dieses Symbol nicht mehr deuten läßt, sondern: ich deute nicht. Ich deute nicht, weil ich mich in dem gegenwärtigen Bild heimisch fühle. Wenn ich deute, so schreite ich auf dem Gedankenweg von Stufe zu Stufe.
235. Sehe ich das gedachte Symbol 'von außen' an, so kommt es mir zum Bewußtsein, daß es so und so gedeutet werden könnte; ist es eine Stufe meines Gedankenweges, so ist es ein mir natürlicher Aufenthalt, und es beschäftigt (und beunruhigt) mich seine weitere Deutbarkeit nicht.—Wie ich die Tabelle, den Fahrplan bei mir habe und verwende, ohne daß es mich beschäftigt, daß eine Tabelle verschiedenerlei Deutungen zuläßt.
236. Wenn ich den Vorgang der Intention beschreiben will, so fühle ich vor allem, daß sie noch am ehesten leisten kann, was sie soll, wenn sie ein äußerst getreues Bild von dem enthält, was sie intendiert. Aber ferner, daß auch das nicht ausreicht, weil ja das Bild, was immer es ist, sich verschieden deuten läßt; daß also dieses Bild doch wieder isoliert dasteht. Wie man das Bild allein ins Auge faßt, ist es plötzlich tot, und es ist, als wäre ihm etwas genommen worden, was es zuvor belebt hatte. Es ist kein Gedanke, keine Intention, und wie immer wir es uns begleitet denken, durch artikulierte oder unartikulierte Vorgänge, und durch welche Empfindungen immer: es bleibt isoliert, weist nicht aus sich heraus auf eine Realität außer ihm.
Nun sagt man: "Freilich intendiert das Bild nicht, sondern wir müssen mit ihm etwas intendieren". Aber wenn dieses Intendieren, Meinen wieder etwas ist, was mit dem Bild geschieht, so sehe ich nicht ein, warum das an einen Menschen gebunden sein soll. Man kann ja auch den Vorgang der Verdauung als chemischen Prozeß studieren, unabhängig davon, ob er in einem Lebewesen stattfindet. Wir wollen sagen "Das Meinen ist doch wesentlich ein geistiger Vorgang, ein Vorgang des bewußten Lebens, nicht der toten Materie". Aber was soll einen solchen ausmachen, als die spezifische Art dessen, was vorgeht—solange wir eben an einen Vorgang denken. Und nun scheint es uns, als ob gar kein Vorgang, welcher Art immer, das Intendieren sein kann.—Wir sind eben hier mit der Grammatik des Vorgangs nicht zufrieden, und nicht mit der spezifischen Art eines Vorgangs.—Man könnte sagen: jeden Vorgang würden wir in diesem Sinne "tot" nennen!
237. Fast könnte man sagen: "Die Meinung geht, während jeder Vorgang steht".
238. Man sagt: Wie kann denn diese Gebärde, diese Haltung der Hand, dieses Bild der Wunsch sein, daß das und das der Fall wäre? Sie ist weiter nichts als eine Hand über einem Tisch und steht allein und ohne Sinn da! Wie eine einzelne Kulisse, die von der Aufführung eines Theaterstücks allein in einem Zimmer stehengeblieben ist. Sie hatte Leben nur im Stück.
239. "Der Gedanke stand in diesem Augenblick vor meiner Seele."—Und wie?—"Ich hatte dieses Bild."—So war das Bild der Gedanke? Nein; denn hätte ich einem bloß das Bild mitgeteilt, so hätte er nicht den Gedanken erhalten.
240. Das Bild war der Schlüssel. Oder es erschien doch als Schlüssel.
241. Denken wir uns eine Bildergeschichte in schematischen Bildern, also ähnlicher der Erzählung in einer Sprache, als eine Folge realistischer Bilder. Man könnte in so einer Bildersprache etwa insbesondere den Gang von Schlachten festgehalten haben. (Sprachspiel.) Und ein Satz unserer Wortsprache kommt so cinem Bild dieser Bildersprache viel näher als man meint.
242. Denken wir auch daran, daß wir uns solche Bilder nicht erst in realistische übertragen, um sie zu verstehen', so wenig wir uns je Photographien oder die Bilder eines Films in farbige Bilder übertragen, obwohl uns schwarz-weiße Menschen oder Pflanzen in der Wirklichkeit unsagbar fremd und schrecklich vorkämen.
Wie, wenn wir nun hier sagten "Ein Bild ist etwas nur in einer Bildersprache"?
243. Gewiß, ich lese eine Geschichte und kümmere mich den Teufel um ein System der Sprache. Ich lese einfach, habe Eindrücke, sehe Bilder vor mir, etc. Ich lasse die Geschichte an mir vorüberziehen wie Bilder, wie eine Bildergeschichte. (Damit will ich natürlich nicht sagen, daß jeder Satz in mir ein visuelles Bild oder mehrere hervorruft, und daß das etwa der Zweck eines Satzes sei.)
244. "Sätze dienen ja dazu zu beschreiben, wie sich alles verhält", denken wir. Der Satz als Bild.
245. Ich verstehe dieses Bild genau, ich könnte es in Ton modellieren.—Ich verstehe diese Beschreibung genau, ich könnte eine Zeichnung nach ihr machen.
Man könnte in vielen Fällen als Kriterium des Verstehens festsetzen, daß man den Sinn des Satzes muß zeichnerisch darstellen können. (Ich denke etwa an eine offiziell festgelegte Prüfung des Verstehens.) Wie wird man z. B. im Kartenlesen geprüft?
246. Und das sinnvolle Bild ist das, was ich nicht nur zeichnen, sondern auch plastisch darstellen kann. Und dies zu sagen hätte Sinn. Aber das Denken des Satzes ist nicht eine Tätigkeit, die man nach den Worten vollzieht (wie etwa das Singen nach den Noten). Das folgende Beispiel zeigt dies. Hat es Sinn zu sagen "Ich habe so viele Freunde, als eine Lösung der Gleichung ..... ergibt"? Ob dies Sinn hat, ist der Gleichung unmittelbar nicht anzusehen. Und man weiß, während man den Satz liest, nicht, ob er sich denken läßt oder nicht. Ob er sich verstehen läßt oder nicht.
247. Was heißt es denn: "entdecken, daß ein Satz keinen Sinn har"?
Und was heißt das: "wenn ich etwas damit meine, muß es doch Sinn haben":
Das Erste heißt doch: sich durch die Erscheinung eines Satzes nicht irren lassen und seine Anwendung im Sprachspiel untersuchen.
Und "wenn ich etwas damit meine"—heißt das etwas Ähnliches wie: "wenn ich mir etwas dabei vorstellen kann"?—Von der Vorstellung führt oft ein Weg zur weiteren Verwendung.
248. (Etwas, was auf den ersten Blick ausschaut wie ein Satz und keiner ist.) Der folgende Vorschlag zur Konstruktion einer Straßenwalze wurde mir einmal mitgeteilt. Der Motor befindet sich im Innern der hohlen Walze. Die Kurbelwelle läuft durch die Mitte der Walze und ist an beiden Enden durch Speichen mit dem Walzenrand verbunden. Der Zylinder des Motors ist an der Innenseite der Walze befestigt. Auf den ersten Blick sieht diese Konstruktion wie eine Maschine aus. Aber sie ist ein starres System, und der Kolben kann sich im Zylinder nicht aus und ein bewegen. Wir haben ihn der Bewegungsmöglichkeit beraubt und wissen es nicht.
249. "Nichts leichter, als sich einen 4-dimensionalen Würfel vorstellen! Er schaut so aus:[1]
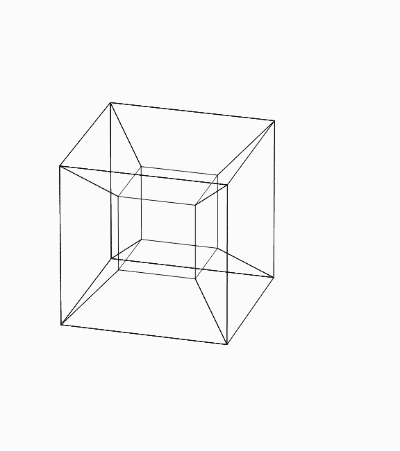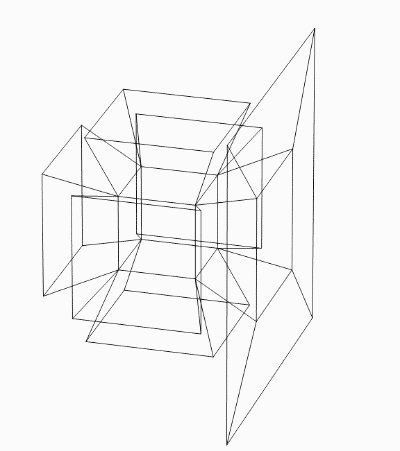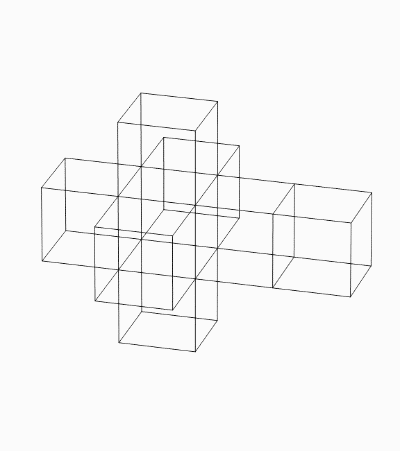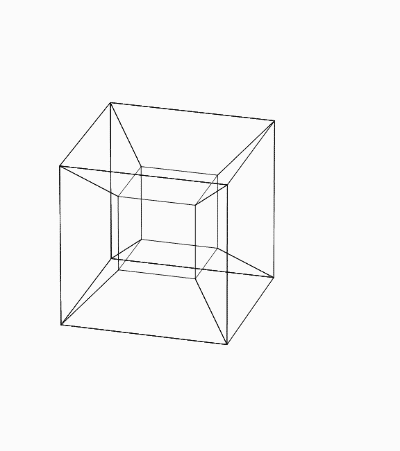
".
Aber das meine ich nicht, ich meine etwas wie
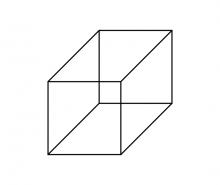
nur mit 4 Ausdehnungen!—"Aber ist nicht, was ich dir gezeigt habe, eben etwas wie

nur mit 4 Ausdehnungen?"—Nein; das meine ich nicht!——Was aber meine ich? Was ist mein Bild? Nun, der 4-dimensionale Würfel, wie du ihn gezeichnet hast, ist es nicht! Ich habe jetzt als Bild nur die Worte und die Ablehnung alles dessen, was du mir zeigen kannst.
250. Sind die Rosen rot im Finstern?—Man kann an die Rose im Finstern als rot denken.—
(Daß man sich etwas 'denken' kann, sagt nicht, daß es Sinn hat, es zu sagen.)
251. "Die Annahme, daß dieser Mensch—der sich ganz normal benimmt—dennoch blind ist, hat doch Sinn!"—D. h.: 'es ist doch eine Annahme', 'ich kann doch so etwas wirklich annehmen'. Und das heißt: ich mache mir doch ein Bild von dem, was ich annehme. Wohl, aber geht es weiter? Wenn ich die Annahme, daß einer blind ist, unter andern Umständen mache, bestätige ich mir doch nie, daß diese Annahme wirklich Sinn hat. Und daß ich mir dabei wirklich etwas denke, ein Bild habe, spielt dann gar keine Rolle. Dieses Bild wird erst hier wichtig, wo es sozusagen der einzige Anhaltspunkt dafür ist, daß ich wirklich eine Annahme gemacht habe. Ja es ist alles, was von der Annahme hier noch übrig ist.
252. "Ich kann mir sehr wohl vorstellen, daß einer so handelt und doch nichts Schandbares in der Handlung sieht."—Und nun folgt eine Beschreibung, wie man sich das vorzustellen habe.
"Ich kann mir eine menschliche Gesellschaft vorstellen, in welcher es als unanständig gilt zu rechnen, außer zum Zeitvertreib." Das heißt ungefähr soviel wie: ich könnte mir dies Bild leicht weiter ausmalen.
253. "Ich habe tatsächlich nie gesehen, daß ein schwarzer Fleck allmählich heller wird, bis er weiß ist, dann das Weiß immer rötlicher, bis er rot ist. Aber ich weiß, daß es möglich ist, weil ich es mir vorstellen kann."
254. (Wenn man mit jemandem über eine Zeiteinteilung redet, so geschieht es oft, daß man die Uhr zieht, nicht um zu sehen, wieviel Uhr es ist, sondern um sich ein Bild der überdachten Einteilung machen zu können.)
255. Wie kann man durch Denken die Wahrheit lernen? Wie man ein Gesicht besser sehen lernt, wenn man es zeichnet.
256. Die Philosophen, die glauben, daß man im Denken die Erfahrung gleichsam ausdehnen kann, sollten daran denken, daß man durchs Telefon die Rede, aber nicht die Masern übertragen kann.
Ich kann auch nicht die Zeit als begrenzt empfinden, wenn ich will, oder das Gesichtsfeld als homogen etc.
257. Wäre es möglich, eine neue Farbe zu entdecken? (Denn der Farbenblinde ist ja in derselben Lage wie wir, seine Farben bilden ein ebenso komplettes System, wie die unsern; er sieht keine Lücke, wo die übrigen Farben noch hinein gehörten.)
(Vergleich mit der Mathematik.)
258. Man kann in der Logik die Allgemeinheit nicht weiter ausdehnen, als unsere logische Voraussicht reicht. Oder richtiger: als unser logischer Blick reicht.
259. "Wie aber kann der menschliche Verstand der Wirklichkeit vorausfliegen, und selbst das Unverifizierbare denken?"—Warum sollen wir nicht das Unverifizierbare reden? Wir machten es ja selbst unverifizierbar.
Es wird ein falscher Schein erzeugt? Und wie kann es auch nur So scheinen? Willst du denn nicht sagen, daß dies so auch nicht einmal eine Beschreibung ist? Nun, dann ist es also kein falscher Schein, sondern vielmehr einer, der uns der Orientierung beraubt. So daß wir uns an den Kopf greifen und eben fragen: Wie ist es möglich?
260. Man kann nur scheinbar "über jede mögliche Erfahrung hinausgehen"; ja, dieses Wort hat auch nur scheinbar Sinn, weil es nach Analogie sinnvoller Ausdrücke gebildet ist.
261. Die "Philosophie des Als Ob" beruht ganz auf dieser Verwechslung zwischen Gleichnis und Wirklichkeit.
262. "Ich kann doch nicht in den Gedanken, durch Worte, eine Voraussicht erschleichen von etwas, was ich nicht kenne.
(Nihil est in intellectu .....)
Als könnte ich in den Gedanken gleichsam von hinten herum kommen und einen Blick von etwas erhaschen, was von vorn zu sehen unmöglich ist."
263. Daher ist auch etwas daran richtig, daß die Unvorstellbarkeit ein Kriterium der Unsinnigkeit ist.
264. Wie, wenn einer sagte: "Ich kann mir nicht vorstellen, wie das ist, wenn man einen Sessel sieht, außer wenn ich ihn gerade sehe"? Wäre er berechtigt, das zu sagen?
265. Bin ich berechtigt zu sagen, "Ich kann |||||||||| nicht als Gestalt sehen"? Was berechtigt mich dazu? (Was berechtigt den Blinden zu sagen, er könne nicht sehen?)
266. Kannst du dir absolutes Gehör vorstellen, wenn du es nicht hast?—Kannst du es dir vorstellen, wenn du es hast?—Kann ein Blinder sich das Sehen vorstellen? Kann ich mir es vorstellen?—Kann ich mir vorstellen, daß ich so und so spontan reagiere, wenn ich's nicht tue?—Kann ich mir's besser vorstellen, wenn ich's tue? ((Gehört zu der Frage: Kann ich mir vorstellen, daß jemand |||||||||| als artikulierte Gestalt sieht.))
267. Soll es Erfahrungstatsache sein, daß, wer ein Erlebnis hatte, es sich vorstellen kann, und daß es ein Andrer nicht kann? (Wie weiß ich, daß der Blinde sich die Farben vorstellen kann?) Aber: er kann ein Sprachspiel nicht spielen (nicht erlernen). Aber wie? Erfahrungsgemäß oder eo ipso? Das letztere.
268. Was würden wir dem sagen, der behauptete, er könne sich genau vorstellen, wie es ist, absolutes Gehör zu haben, ohne daß er's hat?
269. Wenn man glaubt, sich einen vierdimensionalen Raum vorstellen zu können, warum nicht auch vierdimensionale Farben, das sind Farben, die außer dem Grad der Sättigung, dem Farbton und der Lichtstärke noch eine vierte Bestimmung zulassen?
270. "Wie kann es denn Sinn haben, von einer mir ganz neuen Art der Sinneswahrnehmung zu reden, die ich vielleicht einmal haben werde? Wenn du nämlich nicht etwa vom Sinnesorgan reden willst."
271. Wozu dient ein Satz wie dieser: "Wir können uns die Empfindungen eines Jongleurs wie Rastelli gar nicht vorstellen"?
272. "Es hat Sinn, von einer endlosen Baumreihe zu reden; ich kann mir doch vorstellen, daß eine Baumreihe ohne Ende weiterläuft." D. h. etwa: Wenn es Sinn hat zu sagen, die Baumreihe komme hier zu einem Ende, hat es Sinn zu sagen, [sie komme nie zu einem Ende].[2] Ramsey pflegte auf solche Fragen zu antworten: es sei eben doch möglich, so etwas zu denken. So etwa, wie man sagt "Die Technik leistet heute eben Dinge, die du dir gar nie vorstellen kannst."——Nun, da muß man herausfinden, was du dabei denkst. (Daß du versicherst, diese Phrase ließe sich denken—was kann ich damit machen? Darauf kommt es ja nicht an. Ihr Zweck ist ja nicht der, Nebel in deiner Seele aufsteigen zu lassen.) Was du meinst—Wie ist es herauszufinden? Wir müssen geduldig prüfen, wie dieser Satz angewandt werden soll. Wie rund um ihn alles aussieht. Da wird sich sein Sinn zeigen.
273. Hardy: "That 'the finite cannot understand the infinite' should surely be a theological and not a mathematical war-cry." Es ist wahr, dieser Ausdruck ist ungeschickt. Aber was Leute damit sagen wollen, ist: "Es muß hier doch mit rechten Dingen zugehen! Woher dieser Sprung von Endlichen zum Unendlichen?" Und so ganz unsinnig ist die Ausdrucksweise auch nicht—nur ist das 'Endliche', was das Unendliche nicht soll denken können, nicht der Mensch', oder 'unser Verstand', sondern der Kalkül. Und wie dieser das 'Unendliche' denkt, dies ist wohl einer Untersuchung wert. Und die ist zu vergleichen der genauen Untersuchung und Klärung der Geschäftsgebarung eines Unternehmens durch einen Chartered Accountant. Das Ziel ist eine übersichtliche, vergleichende Darstellung aller Anwendungen, Illustrationen, Auffassungen des Kalküls. Die vollkommene Übersicht über alles, was Unklarheit schaffen kann. Und diese Übersicht muß sich auf ein weites Gebiet erstrecken, denn die Wurzeln unserer Ideen reichen weit.—"Das Endliche kann nicht das Unendliche verstehen", heißt hier: So kann es nicht zugehen, wie ihr es in charakteristischer Oberflächlichkeit darstellt.
Der Gedanke kann gleichsam fliegen, er braucht nicht zu gehen. Du verstehst, d. h. übersiehst deine Transaktionen nicht und projizierst quasi dein Unverständnis in die Idee eines Mediums, in dem das Erstaunlichste möglich ist.
274. Das 'wirklich Unendliche' ist ein 'bloßes Wort'. Besser wäre zu sagen: dieser Ausdruck schafft vorläufig bloß ein Bild,—das noch in der Luft hängt; dessen Anwendung du uns noch schuldig bist.
275. Eine unendlich lange Kugelreihe, ein unendlich langer Stab. Denk dir, davon sei in einer Art Märchen die Rede. Welche Anwendung könnte man, wenn auch nur fiktiv, von diesem Begriff machen? Die Frage sei jetzt nicht: Kann es so etwas geben? Sondern: Was stellen wir uns vor? Lass also deiner Einbildung wirklich die Zügel schießen! Du kannst es jetzt haben, wie du's willst. Du brauchst nur zu sagen, wie du's willst. Mach also (nur) ein Wortbild; illustrier es, wie du willst—durch Zeichnungen, durch Vergleiche etc.! Du kannst also—gleichsam—eine Werkzeichnung anfertigen.—Und nun ist noch die Frage, wie nach ihr gearbeitet werden soll.
276. Ich glaube, im Reihenstück ganz fein eine Zeichnung zu erblicken, die nurmehr des "u.s.w." bedarf, um in die Unendlichkeit zu reichen.
"Ich erblicke ein Charakteristikum in ihr."—Nun, doch etwas, was dem algebraischen Ausdruck entspricht.—"Ja, aber nichts Geschriebenes, sondern förmlich etwas Ätherisches."—Welches seltsame Bild.—"Etwas, was nicht der algebraische Ausdruck ist, sondern wofür dieser nur eben der Ausdruck ist."
277. Ich erblicke etwas in ihr—ähnlich wie eine Gestalt im Vexierbild. Und sehe ich das, so sage ich "Das ist alles, was ich brauche."—Wer den Wegweiser findet, sucht nun nicht nach einer weiteren Instruktion, sondern er geht. (Und sagte ich statt "er geht" "er richtet sich nun nach ihm", so könnte der Unterschied der beiden nur sein, daß der zweite Ausdruck auf gewisse psychologische Begleiterscheinungen anspielt.)
278. Was heißt es: Man kann eine gerade Strecke beliebig verlängern? Gibt es hier nicht ein "Und so weiter ad inf.", das ganz verschieden ist von dem der mathematischen Induktion? Nach dem Bisherigen bestünde der Ausdruck für die Möglichkeit der Verlängerns, im Sinn der Beschreibung des verlängerten Stückes oder des Verlängerns. Hier scheint es sich nun zunächst gar nicht um Zahlen zu handeln. Ich kann mir denken, daß der Bleistift, der die Strecke zeichnet, seine Bewegung fortsetzt und nun immer so weiter geht. Ist es aber auch denkbar, daß die Möglichkeit nicht besteht, diesen Vorgang mit einem zählbaren Vorgang zu begleiten? Ich glaube nicht.
279. Wann sagen wir: "Die Linie gibt mir das als Regel ein—immer das Gleiche."? Und anderseits: "Sie gibt mir immer wieder ein, was ich zu tun habe—sie ist keine Regel."?
Im ersten Fall heißt es: ich habe keine weitere Instanz dafür, was ich zu tun habe. Die Regel tut es ganz allein; ich brauche ihr nur zu folgen (und folgen ist eben eins). Ich fühle nicht z. B.: es ist seltsam, daß mir die Linie immer etwas sagt.—Der andre Satz sagt: Ich weiß nicht, was ich tun werde; die Linie wird's mir sagen.
280. Man könnte sich denken, daß einer mit solchen Gefühlen multipliziert, richtig multipliziert; immer wieder sagt "Ich weiß nicht—jetzt gibt mir die Regel auf einmal das ein!"—und daß wir antworten: "Freilich; du gehst ja ganz nach der Regel vor."
281. Zu sagen, die Punkte, die dieses Experiment liefert, liegen durchschnittlich auf dieser Linie, z. B. einer Geraden, sagt etwas Ähnliches, wie: "Aus dieser Entfernung gesehen, scheinen sie in einer Geraden zu liegen."
Ich kann von einer Strecke sagen, der allgemeine Eindruck ist der einer Geraden; aber nicht von der Linie ![]() ; obwohl es möglich wäre, sie als Stück einer längeren Linie zu sehen, in der sich die Abweichung von der Geraden verlieren würden. Ich kann nicht sagen: "Dies Linienstück schaut gerade aus, denn es kann das Stück einer Linie sein, die mir als Ganzes den Eindruck der Geraden macht." (Berge auf der Erde und auf dem Mond. Erde eine Kugel.)
; obwohl es möglich wäre, sie als Stück einer längeren Linie zu sehen, in der sich die Abweichung von der Geraden verlieren würden. Ich kann nicht sagen: "Dies Linienstück schaut gerade aus, denn es kann das Stück einer Linie sein, die mir als Ganzes den Eindruck der Geraden macht." (Berge auf der Erde und auf dem Mond. Erde eine Kugel.)
282. "Sie gibt mir verantwortungslos dies oder das ein" heißt: ich kann es dich nicht lehren, wie ich der Linie folge. Ich setze nicht voraus, daß du ihr folgen wirst wie ich, auch wenn du ihr folgst.
283. Was heißt es: verstehen, daß etwas ein Befehl ist, wenn man auch den Befehl selber noch nicht versteht? ("Er meint: ich soll etwas tun—aber was er wünscht, weiß ich nicht.")
284. Der Satz "Ich muß den Befehl verstehen, ehe ich nach ihm handeln kann", hat natürlich einen guten Sinn; aber wieder keinen metalogischen.
285. Die Idee, die man dabei vom Verstehen hat, ist etwa, daß man dadurch von den Worten näher an die Ausführung heran kommt.—In welchem Sinne ist das richtig?
286. "Aber ich muß einen Befehl verstehen, um nach ihm handeln zu können." Hier ist das "Muß" verdächtig.—
Denk auch an die Frage: "Wie lange vor dem Befolgen mußt du den Befehl verstehen?"
287. "Ich kann den Befehl nicht ausführen, weil ich nicht verstehe, was du meinst.——Ja, jetzt verstehe ich dich."—Was ging da vor, als ich plötzlich den Andern verstand? Da gab es viele Möglichkeiten. Der Befehl konnte z. B. mit falscher Betonung gegeben worden sein; und es fiel mir plötzlich die richtige Betonung ein. Einem Dritten würde ich dann sagen "Jetzt verstehe ich ihn, er meint ....." und würde den Befehl in richtiger Betonung wiederholen. Und in der richtigen Betonung verstünde ich ihn nun; d. h., ich müßte nun nicht noch einen Sinn erfassen (etwas außerhalb des Satzes, also ätherisches), sondern es genügt mir vollkommen der wohlbekannte deutsche Wortlaut.—Oder der Befehl ist mir in verständlichem Deutsch gegeben worden, schien mir aber ungereimt. Dann fällt mir eine Erklärung ein; und nun kann ich ihn ausführen.—Oder es konnten mir mehrere Deutungen vorschweben, für deren eine ich mich endlich entscheide.
288. Wenn der Befehl nicht befolgt wird—wo ist dann der Schatten seiner Befolgung, den du zu sehen meintest; weil dir die Form vorschwebte: Er befiehlt das und das.
289. Wenn die Verbindung des Meinens vor dem Befehl hergestellt werden konnte, dann auch nach dem Befehl.
290. "Er hat das getan, was ich ihm befohlen habe."—Warum soll man hier nicht sagen: es sei eine Identität der Handlung und der Worte?! Wozu soll ich einen Schatten zwischen die beiden stellen? Wir haben ja eine Projektionsmethode.—Nur ist es eine andere Identität: "Ich habe das getan, was er getan hat" und anderseits "Ich habe das getan, was er befohlen hat".
291. "Verbindung des Bildes mit dem Abgebildeten" könnte man die Projektionsstrahlen nennen; aber auch die Technik des Projizierens.
292. Die Doppeldeutigkeit unserer Ausdrucksweise: Wenn uns ein Befehl in einer Chiffer gegeben wäre und der Schlüssel zur Übersetzung ins Deutsche, so könnten wir den Vorgang, den deutschen Befehl zu bilden, mit den Worten bezeichnen: "aus der Chiffer ableiten, was wir zu tun haben", oder "ableiten, welches die Befolgung des Befehls ist". Wenn wir anderseits nach dem Befehl handeln, ihn befolgen, so kann man auch hier in gewissen Fällen von einem Ableiten der Befolgung reden.
293. Ich gebe die Regeln eines Spiels. Der Andere macht, diesen Regeln ganz entsprechend, einen Zug, dessen Möglichkeit ich nicht vorausgesehen hatte, und der das Spiel stört, so wie ich's nämlich wollte. Ich muß nun sagen: "Ich habe schlechte Regeln gegeben"; ich muß meine Regeln ändern oder vielleicht ergänzen.
So habe ich also schon zum Voraus ein Bild des Spiels? In gewissem Sinne: ja!
Es war doch z. B. möglich, daß ich nicht voraussah, daß eine quadratische Gleichung nicht reelle Lösungen haben muß.
Die Regel führt mich also zu etwas, wovon ich sage: "Dieses Bild hatte ich nicht erwartet; ich stellte mir eine Lösung immer so vor: ......"
294. Im einen Fall machen wir den Zug eines bestehenden Spiels, im andern setzen wir eine Spielregel fest. Man könnte auch das Zichen mit einer Spielfigur auf diese beiden Arten auffassen: als Paradigma für künftige Züge, und als Zug einer Partie.
295. Du mußt bedenken, daß es ein Sprachspiel geben kann, 'eine Reihe von Ziffern fortsetzen', in dem keine Regel, kein Regelausdruck je gegeben wird, sondern das Lernen nur durch Beispiele geschieht. So daß die Idee, jeder Schritt sei durch ein Etwas—eine Art Vorbild—in unserm Geiste zu rechtfertigen, diesen Leuten gänzlich fremd wäre.
296. Wie seltsam: Es scheint, als ob zwar eine physische (mechanische) Führung versagen, Unvorhergesehenes zulassen könnte, aber eine Regel nicht! Sie wäre sozusagen die einzig verläßliche Führung. Aber worin besteht es, daß eine Führung eine Bewegung nicht zuläßt und worin, daß eine Regel sie nicht zuläßt?—Wie weiß man das eine, und wie das andere?
297. "Wie mach ich's denn, um ein Wort immer richtig, d. h., sinnvoll anzuwenden; schau ich immer in der Grammatik nach? Nein; daß ich etwas meine—was ich meine, hindert mich, Unsinn zu sagen."—"Ich meine etwas mit den Worten" heißt hier: Ich weiß, daß ich sie anwenden kann.
Ich kann aber glauben, sie anwenden zu können, und es zeigt sich, daß ich im Irrtum war.
298. Daraus folgt nicht, daß Verstehen die Tätigkeit ist, durch die wir unser Verständnis zeigen. Die Frage, ob es diese Tätigkeit ist, ist irreführend. Sie darf nicht so aufgefaßt werden: "Ist also das Verstehen diese Tätigkeit—ist es nicht doch eine andere?"—Sondern so: "Wird 'Verstehen' zur Bezeichnung dieser Tätigkeit gebraucht wird es nicht anders gebraucht?"
299. Wir sagen: "Wenn ihr beim Multiplizieren wirklich der Regel folgt, muß das Gleiche herauskommen." Nun, wenn dies nur die etwas hysterische Ausdrucksweise der Universitätssprache ist, so braucht sie uns nicht sehr zu interessieren. Es ist aber der Ausdruck einer Einstellung zu der Technik des Rechnens, die sich überall in unserm Leben zeigt. Die Emphase des Muß entspricht nur der Unerbittlichkeit dieser Einstellung, sowohl zur Technik des Rechnens, als auch zu unzähligen verwandten Übungen.
300. Mit den Worten: "Diese Zahl ist die folgerechte Fortsetzung dieser Reihe," könnte ich einen dazu bringen, daß er in Zukunft das und das "folgerechte Fortsetzung" nennt. Was 'das und das' ist, kann ich nur an Beispielen zeigen. D. h., ich lehre ihn eine Reihe (Grundreihe) fortsetzen, ohne einen Ausdruck des 'Gesetzes der Reihe' zu verwenden; vielmehr, um ein Substrat zu erhalten für die Bedeutung algebraischer Regeln, oder was ihnen ähnlich ist.
301. Er muß ohne Grund so fortsetzen. Aber nicht, weil man ihm den Grund noch nicht begreiflich machen kann, sondern weil es—in diesem System—keinen Grund gibt. ("Die Kette der Gründe hat ein Ende.")
Und das so (in "so fortsetzen") ist durch eine Ziffer, einen Wert, bezeichnet. Denn auf dieser Stufe wird der Regelausdruck durch den Wert erklärt, nicht der Wert durch die Regel.
302. Denn dort, wo es heißt "Aber siehst du denn nicht .....?" nützt ja eben die Regel nichts, sie ist Erklärtes, nicht Erklärendes.
303. "Er erfaßt die Regel intuitiv."—Warum aber die Regel? Und nicht, wie er jetzt fortsetzen soll?
304. "Hat er nur das Richtige gesehen, diejenige der unendlich vielen Beziehungen, die ich ihm nahezubringen trachte,—hat er sie nur einmal erfaßt, so wird er jetzt ohne weiteres die Reihe richtig fortsetzen. Ich gebe zu, er kann diese Beziehung, die ich meine, nur erraten (intuitiv erraten)—ist es aber gelungen, dann ist das Spiel gewonnen."—Aber dieses Richtige von mir Gemeinte gibt es gar nicht. Der Vergleich ist falsch. Es gibt hier nicht quasi ein Rädchen, das er erfassen soll, die richtige Maschine, die ihn, einmal gewählt, automatisch weiterbringt. Es könnte ja sein, daß sich in unserm Gehirn so etwas abspielt, aber das interessiert uns nicht.
305. "Tu dasselbe!" Aber dabei muß ich ja auf die Regel zeigen. Die muß er also schon anzuwenden gelernt haben. Denn was bedeutet ihr Ausdruck sonst für ihn?
306. Die Bedeutung der Regel erraten, sie intuitiv zu erfassen, könnte doch nur heißen: ihre Anwendung erraten. Und das kann nun nicht heißen: die Art, die Regel ihrer Anwendung erraten. Und vom Erraten ist hier überhaupt keine Rede.
307. Ich könnte z. B. erraten, welche Fortsetzung dem Andern Freude machen wird (etwa nach seinem Gesicht). Die Anwendung der Regel erraten könnte man nur, sofern man bereits unter verschiedenen Anwendungen wählen kann.
308. Man könnte sich ja dann auch denken, daß er, statt die 'Anwendung der Regel zu erraten', sie erfindet. Nun, wie sähe das aus?—Soll er etwa sagen: "Der Regel + 1 folgen, möge einmal heißen zu schreiben: 1, 1+1, 1+1+1, u. s. w."? Aber was meint er damit? Das "u. s. w." setzt ja eben schon das Beherrschen einer Technik voraus.
Statt "u. s. w." hätte er auch sagen können: "Du weißt schon, was ich meine." Und seine Erklärung wäre einfach eine Definition des Ausdrucks "der Regel + 1 folgen" gewesen. Das wäre seine "Erfindung" gewesen.
309. Wir kopieren die Ziffern von 1 bis 100 etwa und schließen, denken auf diese Weise.
Ich könnte es so sagen: Wenn ich die Ziffern von 1 bis 100 kopiere,—wie weiß ich, daß ich eine Ziffernreihe erhalten werde, die beim Zählen stimmt? Und was ist hier eine Kontrolle wofür? Oder wie soll ich hier die wichtige Erfahrungstatsache beschreiben? Soll ich sagen, die Erfahrung lehrt, daß ich immer gleich zähle? Oder, daß beim Kopieren keine Ziffer verloren geht? Oder, daß die Ziffern auf dem Papier stehen bleiben, wie sie sind, auch wenn ich nicht hinschaue? Oder alle diese Tatsachen? Oder soll ich sagen, daß wir einfach nicht in Schwierigkeiten kommen? Oder daß uns fast immer alles in Ordnung zu sein scheint ?
So denken wir. So handeln wir. So reden wir darüber.
310. Denke, du solltest beschreiben, wie Menschen das Zählen (im Dezimalsystem z. B.) lernen. Du beschreibst, was der Lehrer sagt und tut, und wie der Schüler darauf reagiert. In dem, was der Lehrer sagt und tut, werden sich z. B. Worte und Gebärden finden, die den Schüler zum Fortsetzen einer Reihe aufmuntern sollen; auch Worte wie "Er kann jetzt zählen". Soll nun die Beschreibung, die ich von dem Vorgang des Lehrens und Lernens gebe, außer den Worten des Lehrers auch mein eigenes Urteil enthalten: der Schüler könne jetzt zählen oder der Schüler habe nun das System der Zahlworte verstanden? Wenn ich so ein Urteil nicht in die Beschreibung aufnehmen ist sie dann unvollständig? Und wenn ich es aufnehme, gehe ich über die bloße Beschreibung hinaus? Kann ich mich jener Urteile enthalten mit der Begründung: "Das ist alles, was geschieht"?
311. Muß ich nicht vielmehr fragen: "Was tut die Beschreibung überhaupt? Wozu dient sie?"—Was eine vollständige und eine unvollständige Beschreibung ist, wissen wir allerdings in anderem Zusammenhang. Frage dich: Wie verwendet man die Ausdrücke "vollständige" und "unvollständige Beschreibung"?
Eine Rede vollständig (oder unvollständig) wiedergeben. Gehört dazu auch die Wiedergabe des Tonfalls, des Mienenspiels, der Echtheit oder Unechtheit der Gefühle, der Absichten des Redners, der Anstrengung des Redens? Ob das oder jenes für uns zur vollständigen Beschreibung gehört, wird vom Zweck der Beschreibung abhängen, davon, was der Empfänger mit der Beschreibung anfängt.
312. Der Ausdruck "Das ist alles, was geschieht", grenzt ab, was wir "geschehen" nennen.
313. Hier ist die Versuchung überwältigend, noch etwas zu sagen, wenn schon alles beschrieben ist.—Woher dieser Drang? Welche Analogie, welche falsche Interpretation erzeugt ihn?
314. Hier stoßen wir auf eine merkwürdige und charakteristische Erscheinung in philosophischen Untersuchungen: Die Schwierigkeit—könnte ich sagen—ist nicht, die Lösung zu finden, sondern etwas als die Lösung anzuerkennen, was aussieht, als wäre es erst eine Vorstufe zu ihr. "Wir haben schon alles gesagt.—Nicht etwas, was daraus folgt, sondern eben das ist die Lösung!"
Das hängt, glaube ich, damit zusammen, daß wir fälschlich eine Erklärung erwarten; während eine Beschreibung die Lösung der Schwierigkeit ist, wenn wir sie richtig in unsere Betrachtung einordnen. Wenn wir bei ihr verweilen, nicht versuchen, über sie hinauszukommen.
Die Schwierigkeit ist hier: Halt zu machen.
315. "Warum verlangst du Erklärungen? Wenn diese gegeben sein werden, wirst du ja doch wieder vor einem Ende stehen. Sie können dich nicht weiterführen, als du jetzt bist."
316. Man kann einen roten Gegenstand als Muster für das Malen eines rötlichen Weiß oder eines rötlichen Gelb (etc.) verwenden—aber kann man es auch als Muster für das Malen eines blaugrünen Farbtones z. B. verwenden?—Wie, wenn ich jemanden mit allen äußern Zeichen des genauen Kopierens einen roten Fleck blaugrün 'wiedergeben' sähe?—Ich würde sagen "Ich weiß nicht, wie er es macht!" Oder auch "Ich weiß nicht, was er macht!"—Aber angenommen, er 'kopierte' nun diesen Ton von Rot bei verschiedenen Gelegenheiten in Blaugrün und etwa andere Töne von Rot regelmäßig in andern blaugrünen Tönen—soll ich nun sagen, er kopiere, oder er kopiere nicht?
Was heißt es aber, daß ich nicht weiß, 'was er macht'? Sehe ich denn nicht, was er macht?—Aber ich sehe nicht in ihn hinein.—Nur dieses Gleichnis nicht! Wenn ich ihn Rot in Rot kopieren sehe,—was weiß ich denn da? Weiß ich, wie ich es mache? Freilich, man sagt: ich male eben die gleiche Farbe.—Aber wie, wenn er sagt "Und ich male die Quint zu dieser Farbe"? Sehe ich einen besonderen Vorgang der Vermittlung, wenn ich die 'gleiche' Farbe male?
Nimm an, ich kenne ihn als einen ehrlichen Menschen; er gibt, wie ich es beschrieben habe, ein Rot durch ein Blaugrün wieder—aber nun nicht den gleichen Ton immer durch den gleichen, sondern einmal durch einen, einmal durch einen andern Ton.—Soll ich sagen "Ich weiß nicht, was er macht"?—Er macht, was ich sehe—aber ich würde es nie tun; ich weiß nicht, warum er es tut; seine Handlungsweise 'ist mir unverständlich'.
317. Man könnte sich ein negatives Bildnis denken, das ist eines, das darstellen soll, wie Herr N. nicht aussieht (das also ein schlechtes Porträt ist, wenn es dem Herrn N. ähnlich sieht).
318. Ich kann nicht beschreiben, wie eine Regel (allgemein) zu verwenden ist, als indem ich dich lehre, abrichte, eine Regel zu verwenden.
319. Ich kann nun z. B. einen solchen Unterricht im Sprechfilm aufnehmen. Der Lehrer wird manchmal sagen "So ist es recht". Sollte der Schüler ihn fragen "warum?"—so wird er nichts oder doch nichts Relevantes antworten, auch nicht das: "Nun, weil wir's Alle so machen"; das wird nicht der Grund sein.
320. Warum nenne ich die Regeln des Kochens nicht willkürlich, und warum bin ich versucht, die Regeln der Grammatik willkürlich zu nennen? Weil 'Kochen' durch seinen Zweck definiert ist, dagegen 'Sprechen' nicht. Darum ist der Gebrauch der Sprache in einem gewissen Sinne autonom, in dem das Kochen und Waschen es nicht ist. Wer sich beim Kochen nach andern als den richtigen Regeln richtet, kocht schlecht; aber wer sich nach andern Regeln, als denen des Schach richtet, spielt ein anderes Spiel; und wer sich nach andern grammatischen Regeln richtet, als den und den, spricht darum nichts Falsches, sondern von etwas Anderem.
321. Wenn man eine Regel, ein Wort des Satzes betreffend, dem Satz beifügt, so ändert sich sein Sinn nicht.
322. Die Sprache ist für uns nicht als Einrichtung definiert, die einen bestimmten Zweck erfüllt. Sondern "Sprache" ist für uns ein Sammelname, und ich verstehe darunter die deutsche Sprache, die englische Sprache u. s. w. und noch verschiedene Zeichensysteme, die mit diesen Sprachen eine größere oder geringere Verwandtschaft haben.
323. Unsere Kenntnis vieler Sprachen läßt uns die Philosophie, die in den Formen einer jeden niedergelegt sind, nicht recht ernst nehmen. Dabei sind wir aber blind dafür, daß wir selbst starke Vorurteile für, wie gegen gewisse Ausdrucksformen haben, daß eben auch diese besondere Übereinanderlagerung mehrerer Sprachen für uns ein bestimmtes Bild ergibt.
324. Lernt das Kind nur sprechen oder auch denken? Lernt es den Sinn des Multiplizierens vor—oder nach dem Multiplizieren?
325. Wie bin ich denn zum Begriff 'Satz' oder zum Begriff 'Sprache' gekommen? Doch nur durch die Sprachen, die ich gelernt habe.—Aber die scheinen mich in gewissem Sinne über sich selbst hinausgeführt zu haben, denn ich bin jetzt im Stande, eine neue Sprache zu konstruieren, z. B. Wörter zu erfinden.—Also gehört diese Konstruktion noch zum Begriff der Sprache. Aber nur, wenn ich ihn so festlegen will.
326. Der Begriff des Lebewesens hat die gleiche Unbestimmtheit, wie der der Sprache.
327. Vergleiche: Ein Spiel erfinden—eine Sprache erfinden—eine Maschine erfinden.
328. Daß der und der Satz keinen Sinn hat, ist in der Philosophie von Bedeutung; aber auch, daß er komisch klingt.
329. Ich mache einen Plan nicht nur, um mich Andern verständlich zu machen, sondern auch, um selbst über die Sache klar zu werden. (D. h. die Sprache ist nicht nur Mittel zur Mitteilung.)
330. Was heißt das: "Das ist doch nicht mehr dasselbe Spiel!" Wie verwende ich diesen Satz? Als Mitteilung? Nun, etwa als Einleitung zu einer Mitteilung, die die Unterschiede aufzählt und ihre Folgen erklärt. Aber auch um auszudrücken, daß ich eben darum hier nicht mehr mittue, oder doch eine andere Stellung zu dem Spiel einnehme.
331. Man ist versucht, Regeln der Grammatik durch Sätze zu rechtfertigen von der Art "Aber es gibt doch wirklich vier primäre Farben". Und gegen die Möglichkeit dieser Rechtfertigung, die nach dem Modell der Rechtfertigung eines Satzes durch den Hinweis auf seine Verifikation gebaut ist, richtet sich das Wort, daß die Regeln der Grammatik willkürlich sind.
Kann man aber nicht doch in irgendeinem Sinne sagen, daß die Grammatik der Farbwörter die Welt, wie sie tatsächlich ist, charakterisiert? Man möchte sagen: Kann ich nicht wirklich vergebens nach einer fünften primären Farbe suchen? Nimmt man nicht die primären Farben zusammen, weil sie eine Ähnlichkeit haben; oder zum mindesten die Farben, im Gegensatz z. B. zu den Formen oder Tönen, weil sie eine Ähnlichkeit haben? Oder habe ich, wenn ich diese Einteilung der Welt als die richtige hinstelle, schon eine vorgefaßte Idee als Paradigma im Kopf? Von der ich dann etwa nur sagen kann: "Ja, das ist die Art, wie wir die Dinge betrachten", oder "Wir wollen eben ein solches Bild machen". Wenn ich nämlich sage: "die primären Farben haben doch eine bestimmte Ähnlichkeit miteinander"—woher nehme ich den Begriff dieser Ähnlichkeit? Ist nicht so, wie der Begriff 'primäre Farbe' nichts Andres ist, als 'blau oder rot oder grün oder gelb',—auch der Begriff jener Ähnlichkeit nur durch die vier Farben gegeben?—Ja, sind sie nicht die gleichen?—"Ja, könnte man denn auch rot, grün und kreisförmig zusammen. fassen?"—Warum nicht?!
332. Glaub doch nicht, daß du den Begriff der Farbe in dir hältst, weil du auf ein farbiges Objekt schaust,—wie immer du schaust.
(So wenig, wie du den Begriff der negativen Zahl besitzt, dadurch, daß du Schulden hast.)
333. "Rot ist etwas Spezifisches", das müßte soviel heißen, wie: "Das ist etwas Spezifisches"—wobei man auf etwas Rotes deutet. Aber damit das verständlich wäre, müßte man schon unsern Begriff 'rot', den Gebrauch jenes Musters, meinen.
334. Ich kann doch offenbar eine Erwartung einmal in den Worten "ich erwarte einen roten Kreis", ein andermal statt der letzten beiden Worte durch das farbige Bild eines roten Kreises ausdrücken. Aber in diesem Ausdruck entsprechen den beiden Wörtern "rot" und "Kreis" nicht zwei Dinge. Also ist der Ausdruck der zweiten Sprache von ganz anderer Art.
335. Es gäbe außer dieser auch eine Sprache, in der 'roter Kreis' durch Nebeneinanderstellen eines Kreises und eines roten Flecks ausgedrückt würde.
336. Wenn ich nun auch zwei Zeichen bei mir habe, den Ausdruck "roter Kreis" und das farbige Bild, oder die Vorstellung des roten Kreises, so wäre doch die Frage: Wie ist denn dann das eine Wort der Farbe, das andere der Form zugeordnet?
Denn man scheint sagen zu können, das eine Wort lenke die Aufmerksamkeit auf die Farbe, das andere auf die Form. Aber was heißt das? Wie kann man diese Wörter in dieses Bild übersetzen?
Oder auch: Wenn mir das Wort "rot" eine Farbe ins Gedächtnis ruft, so muß sie doch mit einer Form verbunden sein; wie kann ich denn dann von der Form abstrahieren?
Die wichtige Frage ist dabei nie: wie weiß er, wovon er abstrahieren soll? sondern: wie ist das überhaupt möglich? oder: was heißt es?
337. Vielleicht wird es klarer, wenn man die beiden Sprachen vergleicht, in deren einer ein rotes Täfelchen und eines mit einem Kreis darauf (etwa einem schwarzen auf weißem Grund) die Worte "roter Kreis" ersetzen; und in der andren statt dessen ein roter Kreis gemalt wird.
Wie geht denn hier die Übersetzung vor sich? Er schaut etwa zuerst auf das rote Täfelchen und wählt einen roten Stift, dann auf den Kreis, und macht nun mit diesem Stift einen Kreis.
Es würde etwa zuerst gelernt, daß das erste Täfelchen immer die Wahl des Bleistiftes bestimmt, das zweite, was wir mit ihm zeichnen sollen. Die beiden Täfelchen gehören also verschiedenen Wortarten an (etwa Hauptwort und Tätigkeitswort). In der anderen Sprache aber gäbe es nichts, was man hier zwei Wörter nennen könnte.
338. Wenn einer sagte "Rot ist zusammengesetzt"—so könnten wir nicht erraten, worauf er damit anspielt, was er mit diesem Satz wird anfangen wollen. Sagt er aber: "Dieser Sessel ist zusammengesetzt", so mögen wir zwar nicht gleich wissen, von welcher Zusammensetzung er spricht, können aber gleich an mehr als einen Sinn für seine Aussage denken.
Was für eine Art von Faktum ist nun dies, worauf ich aufmerksam machte?
Jedenfalls ist es ein wichtiges Faktum.—Uns ist keine Technik geläufig, auf die dieser Satz anspielen könnte.
339. Wir beschreiben hier ein Sprachspiel, welches wir nicht lernen können.
340. "Dann muß etwas ganz Anderes in ihm vorgehen, etwas, was wir nicht kennen."—Das zeigt ums, wonach wir bestimmen, ob ‘im Andern' etwas Anderes als oder dasselbe wie in uns stattfindet. Das zeigt uns, wonach wir die innern Vorgänge beurteilen.
341. Kannst du dir vorstellen, was der rot-grün Blinde sieht? Kannst du das Bild des Zimmers malen, wie er es sieht?
Kann er es malen, wie er es sieht? Kann ich also malen, wie ich es sehe? In welchem Sinne kann ich es?
342. "Wer alles nur grau, schwarz und weiß sähe, dem müßte etwas gegeben werden, damit er wüßte, was rot, grün etc. ist." Und was müßte ihm gegeben werden? Nun, die Farben. Also z. B. dies und dies und dies. (Denk dir, z. B., daß farbige Vorbilder in sein Gehirn eingeführt werden müßten zu den bloß grauen und schwarzen.) Aber müßte das geschehen als Mittel zum Zweck des künftigen Handelns? Oder schließt eben dieses Handeln diese Vorbilder ein? Will ich sagen: "Es müßte ihm etwas gegeben werden, denn es ist klar, er könnte sonst nicht ...."—oder: Sein sehendes Benehmen enthält neue Bestandteile?
343. Auch: was würden wir eine "Erklärung des Sehens" nennen? Soll man sagen: Nun, du weißt doch sonst, was "Erklärung" heißt; verwende diesen Begriff also auch hier!
344. Kann ich sagen: "Schau es an! so wirst du sehen, daß es sich nicht erklären läßt."—Oder: "Trinke die Farbe Rot in dich ein, so wirst du sehen, daß sie nicht durch etwas Anderes darzustellen ist!"——Und wenn der Andere nun mir beistimmt, zeigt es, daß er dasselbe eingetrunken hat, wie ich?—Und was bedeutet nun unsere Geneigtheit, dies zu sagen? Rot erscheint uns isoliert dazustehen. Warum? Was ist dieser Schein, diese Geneigtheit wert?
Man könnte aber fragen: Auf welche Eigentümlichkeit des Begriffs deutet diese unsre Neigung?
345. Denke an den Satz "Rot ist keine Mischfarbe" und an seine Funktion.
Das Sprachspiel mit den Farben ist eben durch das charakterisiert, was wir tun können, und was wir nicht tun können.
346. "Ein rötliches Grün gibt es nicht", ist den Sätzen verwandt, die wir als Axiome in der Mathematik gebrauchen.
347. Daß wir mit gewissen Begriffen rechnen, mit andern nicht, zeigt nur, wie verschiedener Art die Begriffswerkzeuge sind (wie wenig Grund wir haben, hier je Einförmigkeit anzunehmen). [Randbemerkung: Zu Sätzen über Farben, die den mathematischen ähnlich sind, z. B.: Blau ist dunkler als weiß. Dazu Goethes Farbenlehre.]
348. "Die Möglichkeit der Übereinstimmung bedingt schon eine Übereinstimmung."—Denke, jemand sagte: "Schachspielenkönnen ist eine Art des Schachspielens"!
349. Es ist sehr schwer, Gedankenbahnen zu beschreiben, wo schon viel Fahrgeleise sind—ob deine eigenen oder andere—und nicht in eins der ausgefahrenen Geleise zu kommen. Es ist schwer: nur wenig von einem alten Gedankengeleise abzuweichen.
350. "Es ist, als wären unsere Begriffe bedingt durch ein Gerüst von Tatsachen."
Das hieß doch: Wenn du dir gewisse Tatsachen anders denkst, sie anders beschreibst, als sie sind, dann kannst du die Anwendung gewisser Begriffe dir nicht mehr vorstellen, weil die Regeln ihrer Anwendung kein Analogon unter den neuen Umständen haben.—Was ich sage, kommt also darauf hinaus: Ein Gesetz wird für Menschen gegeben, und ein Jurist mag wohl fähig sein, Konsequenzen für jeden Fall zu ziehen, der ihm gewöhnlich vorkommt, das Gesetz hat also offenbar seine Verwendung, einen Sinn. Trotzdem aber setzt seine Gültigkeit allerlei voraus; und wenn das Wesen, welches er zu richten hat, ganz vom gewöhnlichen Menschen abweicht, dann wird z. B. die Entscheidung, ob er eine Tat mit böser Absicht begangen hat, nicht etwa schwer, sondern (einfach) unmöglich werden.
351. "Wenn die Menschen nicht im allgemeinen über die Farben der Dinge übereinstimmten, wenn Unstimmigkeiten nicht Ausnahmen wären, könnte es unsern Farbbegriff nicht geben." Nein:—gäbe es unsern Farbbegriff nicht.
352. Will ich also sagen, gewisse Tatsachen seien gewissen Begriffsbildungen günstig oder ungünstig? Und lehrt das die Erfahrung? Es ist Erfahrungstatsache, daß Menschen ihre Begriffe ändern, wechseln, wenn sie neue Tatsachen kennenlernen; wenn dadurch, was ihnen früher wichtig war, unwichtig wird und umgekehrt. (Man findet z. B.: was früher als Artunterschied galt, sei eigentlich nur ein Gradunterschied.)
353. Aber kann man nicht sagen: "Wenn es nur eine Substanz gäbe, so hätte man keinen Gebrauch für das Wort 'Substanz'"? Aber das heißt doch: Der Begriff 'Substanz' setzt den Begriff 'Unterschied der Substanz' voraus. (Wie der des Schachkönigs den des Schachzuges, oder wie der der Farbe den der Farben.)
354. Zwischen Grün und Rot, will ich sagen, sei eine geometrische Leere, nicht eine physikalische.
355. Aber entspricht dieser also nichts Physikalisches? Das leugne ich nicht. (Und wenn es bloß unsre Gewöhnung an diese Begriffe ist, an diese Sprachspiele wäre. Aber ich sage nicht, daß es so ist.) Wenn wir einem Menschen die und die Technik durch Exempel beibringen,—daß er dann mit einem bestimmten neuen Fall so und nicht so geht, oder daß er dann stockt, daß für ihn also dies und nicht jenes die 'natürliche' Fortsetzung ist, ist allein schon ein höchst wichtiges Naturfaktum.
356. "Aber wenn ich mit 'bläulichgelb' grün meine, so fasse ich eben diesen Ausdruck anders als nach der ursprünglichen Weise auf. Die ursprüngliche Auffassung bezeichnet einen andern und eben nicht gangbaren Weg."
Was ist aber hier das richtige Gleichnis? Das vom physisch nicht gangbaren Weg, oder vom Nichtexistieren des Weges? Also das Gleichnis der physikalischen oder der mathematischen Unmöglichkeit?
357. Wir haben ein System der Farben wie ein System der Zahlen.
Liegen die Systeme in unserer Natur oder in der Natur der Dinge? Wie soll man's sagen?—Nicht in der Natur der Zahlen oder Farben.
358. Hat denn dieses System etwas Willkürliches? Ja und nein. Es ist mit Willkürlichem verwandt und mit Nichtwillkürlichem.
359. Es leuchtet auf den ersten Blick ein, daß man nichts als Zwischenfarben von rot und grün erkennen will. (Und ob es mir immer so eingeleuchtet oder erst nach Erfahrung und Erziehung, ist gleichgültig.)
360. 'a ist zwischen b und c, und dem b näher als dem c', dies ist eine charakteristische Relation zwischen Empfindungen gleicher Art. D. h., es gibt z. B. ein Sprachspiel mit dem Befehl "Erzeuge eine Empfindung zwischen dieser und dieser, und der ersten näher als der zweiten!" Und auch "Nenne zwei Empfindungen, zwischen welchen diese liegt".
361. Und da ist es wichtig, daß man z. B. bei Grau "Schwarz und Weiß" zur Antwort kriegen wird; bei Violett "Blau und Rot", bei Rosa "Rot und Weiß" etc.; aber nicht bei Olivegrün "Rot und Grün".
362. Die Leute kennen ein Rötlichgrün.—"Aber es gibt doch gar keins!"—Welch sonderbarer Satz.—(Wie weißt du's nur?)
363. Sagen wir's doch einmal so: Müssen denn diese Leute die Diskrepanz merken? Vielleicht sind sie zu stumpf dazu. Und dann wieder: vielleicht auch nicht.—
364. Ja aber hat denn die Natur hier gar nichts mitzureden?! Doch—nur macht sie sich auf andere Weise hörbar.
"Irgendwo wirst du doch an Existenz und nicht-Existenz anrennen!" Das heißt aber doch an Tatsachen, nicht an Begriffe.
365. Es ist eine Tatsache von der höchsten Wichtigkeit, daß eine Farbe, die wir (z. B.) "rötlichgelb" zu nennen geneigt sind, sich wirklich durch Mischung (auf verschiedene Weise) von Rot und Gelb erzeugen läßt. Und daß wir nicht im Stande sind, eine Farbe, die durch Mischen von Rot und Grün entstanden ist, ohne Weiteres als eine zu erkennen, die sich so erzeugen läßt. (Was aber bedeutet "ohne Weiteres" hier?)
366. Verwirrung der Geschmäcke: Ich sage "Das ist süß", der Andere "Das ist sauer" u. s. f. Einer kommt daher und sagt: "Ihr habt alle keine Ahnung, wovon ihr sprecht. Ihr wißt gar nicht mehr, was ihr einmal einen Geschmack genannt habt." Was wäre das Zeichen dafür, daß wir's noch wissen? (Hängt mit einer Frage über eine Verwirrung im Rechnen zusammen.)
367. Aber könnten wir nicht auch in dieser 'Verwirrung' ein Sprachspiel spielen?—Aber ist es noch das Frühere?—
368. Denken wir uns Menschen, die eine Zwischenfarbe von Rot und Gelb z. B., durch eine Art binären Dezimalbruch so ausdrücken: R,LLRL u. dergl., wo auf der rechten Seite z. B. Gelb steht, auf der linken Rot.—Diese Leute lernen schon im Kindergarten, Farbtöne in dieser Weise beschreiben, nach solchen Beschreibungen Farben auszuwählen, zu mischen etc. Sie verhielten sich zu uns ungefähr, wie Leute mit absolutem Gehör zu Leuten, denen dies fehlt. Sie können tun, was wir nicht können.
369. Und hier möchte man sagen: "Ist das denn aber auch vorstellbar? Ja, das Benehmen wohl! Aber auch der innere Vorgang, das Farberlebnis?" Und was man auf so eine Frage sagen soll, ist schwer zu sehen. Hätten die, die kein absolutes Gehör haben, vermuten können, es werde auch Leute mit absolutem Gehör geben?
370. Der Glanz oder die Spiegelung: Wenn ein Kind malt, so wird es diese nie malen. Ja, es ist beinahe schwer zu glauben, daß sie durch die gewöhnlichen Öl- oder Wasserfarben dargestellt werden können.
371. Wie würde eine Gesellschaft von lauter tauben Menschen aussehen? Wie, eine Gesellschaft von 'Geistesschwachen'? Wichtige Frage! Wie also eine Gesellschaft, die viele unserer gewöhnlichen Sprachspiele nie spielte?
372. Den Schwachsinnigen stellt man sich unter dem Bild des Degenerierten, wesentlich Unvollständigen, gleichsam Zerlumpten vor. Also unter dem der Unordnung statt der primitiveren Ordnung (welches eine weit produktivere Anschauungsart wäre).
Wir sehen eben nicht eine Gesellschaft solcher Menschen.
373. Andere, obgleich den unsern verwandte Begriffe könnten uns sehr seltsam erscheinen; Abweichungen nämlich vom Gewohnten in ungewohnter Richtung.
374. Festbegrenzte Begriffe würden eine Gleichförmigkeit des Verhaltens fordern. Aber wo ich sicher bin, ist der Andere unsicher. Und das ist eine Naturtatsache.
375. Dies sind die festen Schienen, auf denen all unser Denken verläuft, und also nach ihnen auch unser Urteilen und Handeln.
376. Dort z. B., wo es einen Typus nur selten gibt, wird der Begriff dieses Typus nicht gebildet. Die Leute berührt dies nicht als eine Einheit, als ein bestimmtes Gesicht.
377. Sie machen davon nicht ein Bild und erkennen es von Fall zu Fall wieder.
378. Muß der Begriff der Bescheidenheit oder der Prahlerei überall bekannt sein, wo es bescheidene und prahlerische Menschen gibt? Es liegt ihnen vielleicht dort nichts an dieser Unterscheidung.
Uns sind ja auch manche Unterschiede unwichtig und könnten uns wichtig sein.
379. Und Andere haben Begriffe, die unsere Begriffe durchschneiden.
380. Ein Stamm hat zwei Begriffe, verwandt unserm 'Schmerz'. Der eine wird bei sichtbaren Verletzungen angewandt und ist mit Pflege, Mitleid etc. verknüpft. Den andern wenden sie bei Magenschmerzen z. B. an, und er verbindet sich mit Belustigung über den Klagenden. "Aber merken sie denn wirklich nicht die Ähnlichkeit?"—Haben wir denn überall einen Begriff, wo eine Ähnlichkeit besteht? Die Frage ist: Ist ihnen die Ähnlichkeit wichtig? Und muß sie's ihnen sein? Und warum sollte nicht ihr Begriff unsern Begriff 'Schmerz' schneiden?
381. Aber übersieht dieser dann nicht etwas, was da ist?—Er nimmt davon keine Notiz; und warum sollte er?—Aber dann ist ja eben sein Begriff grundverschieden von dem unsern.—Grundverschieden? Verschieden.—Aber es ist dann doch, als ob sein Wort nicht dasselbe bezeichnen könnte wie unseres. Oder nur einen Teil davon.—Aber so muß es ja auch ausschauen, wenn sein Begriff verschieden ist. Denn die Unbestimmtheit unseres Begriffs kann sich ja für uns in den Gegenstand projezieren, den das Wort bezeichnet. So daß, fehlte die Unbestimmtheit, auch nicht 'dasselbe gemeint' wäre. Das Bild, das wir verwenden, versinnbildlicht die Unbestimmtheit.
382. In der Philosophie darf man keine Denkkrankheit abschneiden. Sie muß ihren natürlichen Lauf gehen, und die langsame Heilung ist das Wichtigste. (Daher die Mathematiker so schlechte Philosophen sind.)
383. Denk dir, es würden die Leute eines Stammes von früher Jugend dazu erzogen, keinerlei Gemütsausdruck zu zeigen. Er ist für sie etwas Kindisches, das abzutun sei. Die Abrichtung sei streng. Man redet von 'Schmerzen' nicht; schon erst recht nicht in der Form einer Vermutung "Vielleicht hat er doch ....". Klagt jemand, so wird er verlacht oder gestraft. Den Verdacht der Verstellung gibt es gar nicht. Klagen ist sozusagen schon Verstellung
384. "Verstellen", könnten jene Leute sagen, "was für ein lächerlicher Begriff!" (Als unterschiede man einen Mord mit einer Kugel von einem mit drei Kugeln.)
385. Klagen ist schon so schlimm, daß es das Schlimmere der Verstellung gar nicht mehr gibt.
386. Die eine Schande steht ihnen vor der andern, diese können sie nicht sehen.
387. Ich will sagen: eine ganz andere Erziehung als die unsere könnte auch die Grundlage ganz anderer Begriffe sein.
388. Denn es würde hier das Leben anders verlaufen.—Was uns interessiert, würde sie nicht interessieren. Andere Begriffe wären da nicht mehr unvorstellbar. Ja, wesentlich andere Begriffe sind nur so vorstellbar.
389. Man könnte [jemanden] doch einfach lehren, den Schmerz (z. B.) zu mimen (nicht in der Absicht zu betrügen). Aber wäre es jedem beizubringen? Ich meine: Er könnte ja wohl erlernen, gewisse rohe Schmerzzeichen von sich zu geben, ohne aber je aus eigenem, aus seiner eigenen Einsicht eine feinere Nachahmung zu geben. (Sprachtalent.) (Man könnte vielleicht einem gescheiten Hund eine Art Schmerzgeheul beibringen; aber es käme doch nie bei ihm zu einem bewußten Nachahmen.)
390. 'Diese Menschen hätten nichts Menschenähnliches.' Warum?—Wir könnten uns unmöglich mit ihnen verständigen. Nicht einmal so, wie wir's mit einem Hund können. Wir könnten uns nicht in sie finden.
Und doch könnte es ja solche, im übrigen menschliche, Wesen geben.
391. Ich will eigentlich sagen, daß die gedanklichen Skrupel im Instinkt anfangen (ihre Wurzeln haben). Oder auch so: das Sprachspiel hat seinen Ursprung nicht in der Überlegung. Die Überlegung ist ein Teil des Sprachspiels.
Und der Begriff ist daher im Sprachspiel zu Hause.
392. 'Sandhaufen' ist ein unscharf begrenzter Begriff——aber warum verwendet man statt seiner nicht einen scharf begrenzten?—Liegt der Grund in der Natur der Haufen? Welche Erscheinung ist es, deren Natur für unsern Begriff maßgebend ist?
393. Man kann sich leicht Ereignisse vorstellen und in alle Einzelheiten ausmalen, die, wenn wir sie eintreten sähen, uns an allem Urteilen irre werden ließen.
Sähe ich einmal von meinem Fenster statt der altgewohnten eine ganz neue Umgebung, benähmen sich die Dinge, Menschen und Tiere, wie sie sich nie benommen haben, so würde ich etwa die Worte äußern "Ich bin wahnsinnig geworden"; aber das wäre nur ein Ausdruck dafür, daß ich es aufgebe, mich auszukennen. Und das Gleiche könnte mir auch in der Mathematik zustoßen. Es könnte mir z. B. scheinen, als machte ich immer wieder Rechenfehler, sodaß keine Lösung mir verläßlich erschiene.
Das Wichtige aber für mich daran ist, daß es zwischen einem solchen Zustand und dem normalen keine scharfe Grenze gibt.
394. Was hieße es, mich darin irren, daß er eine Seele, Bewußt. sein habe? Und was hieße es, daß ich mich irre und selbst keines habe? Was hieße es zu sagen "Ich bin nicht bei Bewußtsein."?——Aber weiß ich nicht doch, daß Bewußtsein in mir ist?—So weiß ich's also, und doch hat die Aussage, es sei so, keinen Zweck?
Und wie merkwürdig, daß man lernen kann, sich in dieser Sache mit andern Leuten zu verständigen!
395. Einer kann sich bewußtlos stellen; aber auch bewußt?
396. Wie wäre es, wenn mir jemand allen Ernstes sagte, er wisse (wirklich) nicht, ob er träume oder wache?—
Kann es diese Situation geben: Einer sagt "Ich glaube, ich träume jetzt"; wirklich wacht er bald danach auf, erinnert sich an jene Äußerung im Traum und sagt "So hatte ich also recht!"——Diese Erzählung kann doch nur besagen: Einer habe geträumt, er hätte gesagt, er träume.
Denke, ein Bewußtloser sagte (etwa in der Narkose) "Ich bin bei Bewußtsein"—würden wir sagen "Er muß es wissen"?
Und wenn Einer im Schlaf spräche "Ich schlafe",—würden wir sagen "Er hat ganz recht"?
Spricht einer die Unwahrheit, der mir sagt: "Ich bin nicht bei Bewußtsein"? (Und die Wahrheit, wenn er's bewußtlos sagt? Und wie, wenn ein Papagei sagte "Ich verstehe kein Wort", oder ein Grammophon "Ich bin bloß eine Maschine"?)
397. Denke, in einem Tagtraum ließe ich mich sprechen "Ich phantasiere bloß", wäre das wahr? Denke, ich schreibe so eine Phantasie oder Erzählung, einen phantasierten Dialog, und in ihm sage ich "Ich phantasiere"——aber, wenn ich es aufschreibe,—wie zeigt sich's, daß diese Worte Worte der Phantasie sind, und daß ich nicht aus der Phantasie herausgetreten bin?
Wäre es nicht wirklich möglich, daß der Träumende, sozusagen aus dem Traum heraustretend, im Schlaf spräche "Ich träume"? Es wäre wohl denkbar, daß so ein Sprachspiel existierte.
Dies hängt mit dem Problem des 'Meinens' zusammen. Denn ich kann im Dialog eines Stücks schreiben "Ich bin gesund" und es also nicht weinen, obwohl es auch wahr ist. Die Worte gehören zu diesem und nicht zu jenem Sprachspiel.
398. 'Wahr' und 'Falsch' im Traum. Ich träume, daß es regnet, und daß ich sage "Es regnet"——anderseits: Ich träume, daß ich sage "Ich träume".
399. Hat das Verbum "träumen" eine Gegenwartsform? Wie lernt der Mensch diese gebrauchen?
400. Angenommen, ich hätte eine Erfahrung, ähnlich einem Erwachen, befände mich dann in einer ganz andern Umgebung, mit Leuten, die mich versichern, ich habe geschlafen. Angenommen ferner, ich bliebe dabei, ich habe nicht geträumt, sondern auf irgendeine Weise außerhalb meines schlafenden Körpers gelebt. Welche Funktion hat diese Behauptung?
401. "'Ich habe Bewußtsein', das ist eine Aussage, an der kein Zweifel möglich ist." Warum soll das nicht das Gleiche sagen, wie dies: "'Ich habe Bewußtsein' ist kein Satz"?
Man könnte auch so sagen: Was schadet es, daß einer sagt, "Ich habe Bewußtsein" sei eine Aussage, die keinen Zweifel zulasse? Wie komme ich mit ihm in Widerspruch? Nimm an, jemand sagte mir dies,—warum soll ich mich nicht gewöhnen, ihm nichts darauf zu antworten, statt etwa einen Streit anzufangen? Warum soll ich seine Worte nicht behandeln, wie sein Pfeifen oder Summen?
402. "Nichts ist so gewiß wie, daß mir Bewußtsein eignet." Warum soll ich es dann nicht auf sich beruhen lassen? Diese Gewißheit ist wie eine große Kraft, deren Angriffspunkt sich nicht bewegt, die also keine Arbeit leistet.
403. Erinnere dich: die meisten sagen, man spüre in der Narkose nichts. Manche aber sagen doch: Man könnte ja doch etwas fühlen und es nur völlig vergessen.
Wenn es also hier solche gibt, die zweifeln und solche, denen kein Zweifel kommt, so könnte die Zweifellosigkeit doch auch viel allgemeiner bestehen.
404. Oder der Zweifel könnte doch eine andere, und viel weniger unbestimmte Form haben, als in unserer Gedankenwelt.
405. Niemand außer ein Philosoph würde sagen "Ich weiß, daß ich zwei Hände habe"; wohl aber kann man sagen: "ich bin nicht imstande zu bezweifeln, daß ich zwei Hände habe".
406. "Wissen" aber wird gewöhnlich nicht in diesem Sinn gebraucht. "Ich weiß, wieviel 97 × 78 ist." "Ich weiß, daß 97 × 78 432 ist." Im ersten Falle teile ich jemandem mit, ich könne etwas, besitze etwas; im zweiten versichere ich einfach, 97 × 78 sei 432. Sagt denn "97 × 78 ist ganz bestimmt 432" nicht, ich wisse, es sei so? Der erste Satz ist kein arithmetischer, noch kann ihn ein solcher ersetzen; statt des zweiten könnte man einen arithmetischen Satz verwenden.
407. Kann jemand glauben, daß 25 × 25 = 625 ist? Was heißt es, das zu glauben? Wie zeigt es sich, daß er das glaubt?
408. Aber gibt es nicht ein Phänomen des Wissens sozusagen ganz abgesehen vom Sinn der Worte "ich weiß"? Ist es nicht merkwürdig, daß ein Mensch etwas wissen kann, die Tatsache gleichsam in sich selbst haben kann?—Aber das ist eben ein falsches Bild.—Denn, sagt man, Wissen ist es nur, wenn es sich wirklich verhält, wie er sagt. Aber das ist nicht genug. Es darf sich nicht nur zufällig so verhalten. Er muß nämlich wissen, daß er weiß: das Wissen ist ja sein eigener Seelenzustand: er kann darüber—außer durch eine besondere Verblendung—nicht im Zweifel oder Unrecht sein. Wenn also das Wissen, daß es so ist, nur ein Wissen ist, wenn es wirklich so ist; und wenn das Wissen in ihm ist, sodaß er sich darin, ob es ein Wissen ist, nicht irren kann; dann ist er (also) auch unfehlbar darin, daß es ist, wie er das Wissen weiß; und also muß die Tatsache, die er weiß, so wie das Wissen in ihm sein.
Und das deutet allerdings auf eine mögliche Art der Verwendung von "Ich weiß". "Ich weiß, daß es so ist", heißt dann: Es ist so oder ich bin verrückt.
Also: wenn ich, ohne zu lügen, sage: "Ich weiß, daß es so ist", so kann ich nur durch eine besondere Verblendung im Unrecht sein.
409. Wie kommt es, daß der Zweifel nicht der Willkür untersteht?—Und wenn es so ist,—könnte nicht ein Kind durch seine merkwürdige Veranlagung an allem zweifeln?
410. Man kann erst zweifeln, wenn man Gewisses gelernt hat; wie man sich erst verrechnen kann, wenn man rechnen gelernt hat. Dann ist es allerdings unwillkürlich.
411. Denke, ein Kind wäre ganz besonders gescheit, so gescheit, daß man ihm gleich die Zweifelhaftigkeit der Existenz aller Dinge beibringen kann. Es lernt also vom Anfangan: "Das ist wahrscheinlich ein Sessel."
Und wie lernt es nun die Frage: "Ist das auch wirklich ein Sessel?"—
412. Betreibe ich Kinderpsychologie?—Ich bringe den Begriff des Lehrens mit dem Begriff der Bedeutung in Verbindung.
413. Einer sei ein überzeugter Realist, der Andere ein überzeugter Idealist und lehrt seine Kinder dementsprechend. In einer so wichtigen Sache, wie der Existenz oder Nichtexistenz der äußern Welt wollen sie ihren Kindern nichts Falsches beibringen.
Was wird man sie nun lehren? Auch dies zu sagen "Es gibt physikalische Gegenstände", beziehungsweise das Gegenteil?
Wenn einer an Feen nicht glaubt, so braucht er seine Kinder nicht lehren "Es gibt keine Feen", sondern er kann es unterlassen, sie das Wort "Fee" zu lehren. Bei welcher Gelegenheit sollen sie sagen "Es gibt ....", oder "Es gibt nicht ...."? Nur wenn sie Leute treffen, die entgegengesetzten Glaubens sind.
414. Aber der Idealist wird den Kindern doch das Wort "Sessel" beibringen, denn er will sie ja lehren, dies und jenes zu tun, z. B. einen Sessel zu holen. Wo wird sich also, was die idealistisch erzogenen Kinder sagen, von dem, was die realistischen sagen, unterscheiden? Wird der Unterschied nicht nur der der Schlachtrufe sein?
415. Fängt denn nicht das Spiel "Das ist wahrscheinlich ein ...." mit der Enttäuschung an? Und kann die erste Einstellung die auf die mögliche Enttäuschung sein?
416. "So muß man ihm also zuerst eine falsche Sicherheit beibringen?"
Es ist bei ihrem Sprachspiel von Sicherheit oder von Unsicherheit noch nicht die Rede. Erinnere dich: sie lernen ja etwas tun.
417. Das Sprachspiel "Was ist das?"—"Ein Sessel."—ist nicht das Gleiche wie: "Wofür hältst du das?"—"Es dürfte ein Sessel sein."
418. Einen im Anfang lehren "Das scheint rot", hat gar keinen Sinn. Das muß er ja spontan sagen, wenn er einmal gelernt hat, was "rot" heißt, d. i. die Technik der Wortverwendung.
419. Die Grundlage jeder Erklärung ist die Abrichtung. (Das sollten Erzieher bedenken.)
420. "Es scheint mir rot."—"Und wie ist rot?"—"So." Dabei muß auf das richtige Paradigma gezeigt werden.
421. Wenn er zuerst die Farbnamen lernt, was wird ihm beigebracht? Nun, er lernt z. B. beim Anblick von etwas Rotem "Rot" ausrufen.—Ist das aber die richtige Beschreibung, oder hätte es heißen sollen: "Er lernt 'rot' nennen, was auch wir 'rot' nennen"?—Beide Beschreibungen sind richtig.
Wie unterscheidet sich davon das Sprachspiel "Wie kommt es dir vor?"?
Man könnte einem doch die Farbwörter beibringen, indem man ihn auf weiße Gegenstände durch farbige Brillen schauen läßt. Was ich ihn aber lehre, muß ein Können sein. Er kann also jetzt auf Befehle etwas Rotes bringen, oder Gegenstände nach ihren Farben ordnen. Aber was ist denn etwas Rotes?
422. Warum lehrt man das Kind nicht zuerst gleich das Sprachspiel "Es scheint mir rot"? Weil es noch nicht imstande ist, den feineren Unterschied zwischen Schein und Sein zu verstehen?
423. Die rote Gesichtsempfindung ist ein neuer Begriff.
424. Das Sprachspiel, was wir ihm dann beibringen, ist: "Mir scheint es ...., dir scheint es ...." Im ersten Sprachspiel kommt eine Person als wahrnehmendes Subjekt nicht vor.
425. Du gibst dem Sprachspiel ein neues Gelenk. Was aber nicht heißt, daß nun davon immer Gebrauch gemacht wird.
426. Das innere Hinblicken auf die Empfindung—welche Verbindung soll es denn zwischen Wort und Empfindung her stellen; und wozu soll denn diese Verbindung dienen? Hat man mich das gelehrt, als ich diesen Satz gebrauchen, diesen Gedanken denken lernte? (Ihn zu denken, ist ja etwas, was ich lernen mußte.)
Wir lernen allerdings auch dies, unsre Aufmerksamkeit auf Dinge und auf Empfindungen richten. Wir lernen beobachten und die Beobachtung beschreiben. Aber wie lehrt man mich dies; wie wird in diesem Falle meine 'innere Tätigkeit' kontrolliert? Wonach wird beurteilt, ob ich wirklich Acht gegeben habe?
427. "Der Sessel ist der gleiche, ob ich ihn betrachte oder nicht"—das müßte nicht wahr sein. Menschen werden oft verlegen, wenn man sie anschaut. "Der Sessel fahrt fort zu existieren, ob ich ihn anschaue oder nicht." Das könnte ein Erfahrungssatz, oder es könnte grammatisch aufzufassen sein. Man kann aber auch einfach an den begrifflichen Unterschied zwischen Sinneseindruck und Objekt dabei denken.
428. Ist aber nicht die Übereinstimmung der Menschen dem Spiel wesentlich? Muß, wer es lernt, also nicht zuerst die Bedeutung von "gleich" kennen, und setzt die nicht auch Übereinstimmung voraus? U. s. f.
429. Du sagst "Das ist rot", aber wie wird entschieden, ob du recht hast? Entscheidet es nicht die Übereinstimmung der Menschen?—Aber berufe ich mich denn auf diese Übereinstimmung in meinen Farburteilen? Geht es denn so vor sich: Ich lasse eine Anzahl Leute einen Gegenstand anschauen; jedem von ihnen fällt dabei eines einer gewissen Gruppe von Wörtern (der sogenannten Farbwörter) ein; ist der Mehrzahl der Betrachter das Wort "rot" z. B. eingefallen (zu dieser Mehrzahl muß ich selbst nicht gehören), so gebührt dem Gegenstand das Prädikat "rot". So eine Technik könnte ja ihre Wichtigkeit haben.
430. Die Farbwörter werden so gelehrt: "Das ist rot" z. B.—Unser Sprachspiel kommt freilich nur zustande, wenn eine gewisse Übereinstimmung herrscht, aber der Begriff der Übereinstimmung tritt ins Sprachspiel nicht ein. Wäre die Übereinstimmung vollkommen, so könnte ihr Begriff ganz unbekannt sein.
431. Entscheidet die Übereinstimmung der Menschen, was rot ist? Wird das durch den Appell an die Mehrheit entschieden? Wurde uns beigebracht, die Farbe so zu bestimmen?
432. Ich beschreibe eben das Sprachspiel "Bring etwas Rotes" dem, der es schon selbst spielen kann. Den Andern könnte ich es nur lehren. (Relativität.)
433. "Was ich wahrnehme, ist dies—" und nun folgt eine Form der Beschreibung. Das Wort "dies" könnte man auch so erklären: Denken wir uns eine direkte Übertragung des Erlebnisses!—Aber was ist nun unser Kriterium dafür, daß das Erlebnis wirklich übertragen wurde? "Nun, er hat eben dann das, was ich habe."—Aber wie 'hat' er es?
434. Was heißt es, "eine Empfindung mit einem Wort bezeichnen, benennen"? Gibt es da nichts zu untersuchen?
Denk dir, du kämest von einem Sprachspiel mit physikalischen Gegenständen—und nun hieße es, es werden jetzt auch Empfindungen benannt. Wäre das nicht, als würde zuerst von einer Übertragung des Besitzes, und dann auf einmal von einer Übertragung der Freude am Besitz oder des Stolzes auf den Besitz gesprochen? Müssen wir da nicht etwas Neues lernen? Etwas Neues, was wir auch "übertragen" nennen.
435. Die Beschreibung des subjektiv Gesehenen ist nahe oder entfernt verwandt der Beschreibung eines Gegenstandes, aber funktioniert eben daher nicht als Beschreibung eines Gegenstands. Wie vergleicht man Gesichtsempfindungen? Wie vergleiche ich meine mit des Andern Gesichtsempfindungen?
436. "Verifying by inspection" ist ein gänzlich irreführender Ausdruck. Er sagt nämlich, daß zuerst ein Vorgang, die Inspektion geschieht, und die wäre mit dem Schauen durch ein Mikroskop vergleichbar oder mit dem Vorgang des Umwendens des Kopfes, um etwas zu sehen. Und, daß dann das Sehen erfolgen misse. Man könnte von "Sehen durch Umwenden" oder "Sehen durch Schauen" reden. Aber dann ist eben das Umwenden (oder Schauen) ein dem Sehen externer Vorgang, der uns daher nur praktisch interessiert. Was man sagen möchte, ist: "Sehen durch Sehen".
437. Die Ursachen, warum wir einen Satz glauben, sind für die Frage, was es denn ist, das wir glauben, allerdings irrelevant; aber nicht die Gründe, die ja mit dem Satz grammatisch verwandt sind und uns sagen, wer er ist.
438. Es ist nichts gewöhnlicher, als daß die Bedeutung eines Ausdrucks in der Weise schwankt, daß ein Phänomen bald als Symptom, bald als Kriterium eines Sachverhalts angesehen wird. Und meistens wird dann in einem solchen Fall der Wechsel der Bedeutung nicht gemerkt. In der Wissenschaft ist es üblich, Phänomene, die genaue Messungen zulassen, zu definierenden Kriterien eines Ausdrucks zu machen; und man ist dann geneigt zu meinen, nun sei die eigentliche Bedeutung gefunden worden. Eine Unmenge von Verwirrungen ist auf diese Weise entstanden.
Es gibt z. B. Grade des Vergnügens, aber es ist dumm, von einer Messung des Vergnügens zu reden. Es ist wahr, daß in gewissen Fällen ein meßbares Phänomen den Platz einnimmt, den vor ihm ein nicht meßbares hatte. Das Wort, das diesen Platz bezeichnet, wechselt dann seine Bedeutung, und seine alte Bedeutung ist mehr oder weniger obsolet geworden. Man beruhigt sich dann damit, der eine Begriff sei der genauere, der andere der ungenauere; und beachtet nicht, daß hier in jedem besondern Fall ein anderes Verhältnis zwischen dem 'genauen' und dem 'ungenauen' vorliegt. Es ist der alte Fehler, die besondern Fälle nicht zu prüfen.
439. Die zureichende Evidenz geht, ohne bestimmte Grenzen zu haben, in die unzureichende über. Soll ich sagen, eine natürliche Grundlage dieser Begriffsbildung sei das komplizierte Wesen und die Mannigfaltigkeit der menschlichen Fälle?
So müßte also bei einer weit geringeren Mannigfaltigkeit eine scharf begrenzte Begriffsbildung natürlich erscheinen. Und warum scheint es so schwer, sich den vereinfachten Fall vorzustellen?
440. Wie hätten wir uns ein komplettes Regelverzeichnis für die Verwendung eines Worts zu denken?—Was versteht man unter einem kompletten Regelverzeichnis für die Verwendung einer Figur im Schachspiel? Könnten wir uns nicht immer Zweifelfalle konstruieren, in denen das normale Regelverzeichnis nicht entscheidet? Denke etwa an so eine Frage: wie ist es festzustellen, wer zuletzt gezogen hat, wenn die Zuverlässigkeit des Gedächtnisses der Spieler angezweifelt wird?
Die Verkehrsregelung in den Straßen erlaubt und verbietet gewisse Handlungen der Fahrer und Fußgänger; aber sie versucht nicht, ihre sämtlichen Bewegungen durch Vorschriften zu leiten. Und es wäre sinnlos, von einer 'idealen' Verkehrsordnung zu reden, die das täte; wir wüßten zunächst gar nicht, was wir uns unter diesem Ideal zu denken hätten. Wünscht einer die Verkehrsordnung in irgendwelchen Punkten strenger zu gestalten, so bedeutet das nicht, er wünsche sie so einem Ideal anzunähern.
441. Betrachte auch diesen Satz: "Die Regeln eines Spiels können wohl eine gewisse Freiheit lassen, aber sie müssen doch ganz bestimmte Regeln sein." Das ist, als sagte man: "Du kannst zwar einem Menschen durch vier Wände eine gewisse Bewegungsfreiheit lassen, aber die Wände müssen vollkommen starr sein"—und das ist nicht wahr. "Nun, die Wände können wohl elastisch sein, aber dann haben sie eine ganz bestimmte Elastizität."—Was sagt das nun doch? Es scheint zu sagen, daß man diese Elastizität muß angeben können, aber das ist wieder nicht wahr. "Die Wand hat immer eine bestimmte Elastizität—ob ich sie kenne oder nicht.": das ist eigentlich das Bekenntnis zu einer Ausdrucksform. Derjenigen, die sich der Form eines Ideals der Genauigkeit bedient. Gleichsam als eines Parameters der Darstellung.
442. Das Bekenntnis zu einer Ausdrucksform, wenn es ausgesprochen wird in der Verkleidung als ein Satz, der von den Gegenständen (statt von dem Zeichen) handelt, muß 'a priori' sein. Denn sein Gegenteil wird wirklich undenkbar, insofern ihm eine Denkform, Ausdrucksform entspricht, die wir ausgeschlossen haben.
443. Denke dir, die Menschen pflegten auf Gegenstände immer in der Weise zu zeigen, daß sie mit dem Finger in der Luft gleichsam einen Kreis um den Gegenstand beschrieben, dann könnte man sich einen Philosophen denken, der sagte: "Alle Dinge sind kreisrund; denn der Tisch sieht so aus, der Öfen so, die Lampe so" etc., indem er jedesmal einen Kreis um das Ding schlägt.
444. Wir haben nun eine Theorie; eine 'dynamische Theorie'[3] des Satzes, der Sprache, aber sie erscheint uns nicht als Theorie. Es ist ja das Charakteristische einer solchen Theorie, daß sie einen besonderen, klar anschaulichen Fall ansieht und sagt: "Das zeigt, wie es sich überhaupt verhält; dieser Fall ist das Urbild aller Fälle."——"Natürlich! So muß es sein", sagen wir und sind zufrieden. Wir sind auf eine Form der Darstellung gekommen, die uns einleuchtet. Aber es ist, als haben wir nun etwas gesehen, was unter der Oberfläche liegt.
Die Tendenz, den klaren Fall zu verallgemeinern, scheint in der Logik ihre strenge Berechtigung zu haben: man scheint hier mit voller Berechtigung zu schließen: "Wenn ein Satz ein Bild ist, so muß jeder Satz ein Bild sein, denn sie müssen alle wesensgleich sein." Denn wir sind ja in der Täuschung, das Sublime, Wesentliche unserer Untersuchung bestehe darin, daß sie ein allumfassendes Wesen erfasse.
445. Wie kann ich den Satz jetzt verstehen, wenn die Analyse soll zeigen können, was ich eigentlich verstehe?—Hier spielt die Idee des Verstehens als eines sonderbaren geistigen Vorgangs hinein.
446. Denk doch einmal gar nicht an das Verstehen als 'seelischen Vorgang'!—Denn das ist die Redeweise, die dich verwirrt. Sondern frage dich: in was für einem Fall, unter was für Umständen sagen wir denn "jetzt weiß ich weiter", wenn uns die Formel eingefallen ist?
Es ist jene Redeweise, die uns hindert, die Tatsachen unparteiisch zu sehen. Betrachte die Aussprache eines Worts durch die Darstellungsform der Schreibung! Wie leicht kann man sich da überreden, daß zwei Worte—z. B. "für" und "führ"—im täglichen Gebrauche verschiedenen Klang haben—weil man sie verschieden ausspricht, wenn man sein Augenmerk gerade auf den Unterschied ihrer Schreibung richtet. Damit zu vergleichen ist die Meinung, ein Violinspieler mit feinem Gehör greife f immer etwas höher als eis. Überlege dir solche Fälle!—So kann es geschehen, daß das Darstellungsmittel eine Einbildung erzeugt. Denken wir also nicht, wir müßten einen spezifischen seelischen Vorgang finden, weil das Verbum "verstehen" dasteht, und weil man sagt: Verstehen sei eine seelische Tätigkeit.
447. Die Unruhe in der Philosophie, könnte man sagen, kommt daher, daß wir die Philosophie falsch ansehen, falsch sehen, nämlich gleichsam in (endlose) Längsstreifen zerlegt, statt in (begrenzte) Querstreifen. Diese Umstellung der Auffassung macht die größte Schwierigkeit. Wir wollen also gleichsam den unbegrenzten Streifen erfassen und klagen, daß es nicht Stück für Stück möglich ist. Freilich nicht, wenn man unter einem Stück einen endlosen Längsstreifen versteht. Wohl aber, wenn man einen Querstreifen darunter versteht.—Aber dann kommen wir ja mit unserer Arbeit wieder nicht zu Ende!—Freilich nicht, denn sie hat keins.
(Statt der turbulenten Mutmaßungen und Erklärungen wollen wir ruhige Erwägung sprachlicher Tatsachen setzen.)
448. Und sagt man denn vom Satz "Es regnet", er sage: es verhält sich so und so? Welches ist denn der alltägliche Gebrauch dieses Ausdrucks in der gewöhnlichen Sprache? Denn von diesem Gebrauch hast ja du ihn gelernt. Verwendest du ihn nun gegen seinen ursprünglichen Gebrauch und denkst, du spielest noch das alte Spiel mit ihm, so ist das, als wenn du mit Schachfiguren Dame spieltest und dir einbildetest, das Spiel habe noch etwas vom Geist des Schach.
449. Ausdehnung eines Begriffs in einer Theorie (z. B. Wunschtraum).
450. Wer philosophiert, macht oft zu einem Wortausdruck die falsche, unpassende Geste.
451. (Man sagt das Gewöhnliche—mit der falschen Gebärde.)
452. Wie kommt es, daß die Philosophie ein so komplizierter Bau ist? Sie sollte doch gänzlich einfach sein, wenn sie jenes Letzte von aller Erfahrung Unabhängige ist, wofür du sie ausgibst.—Die Philosophie löst Knoten auf in unserm Denken; daher muß ihr Resultat einfach sein, das Philosophieren aber so kompliziert wie die Knoten, welche es auflöst.
453. (Wie man manchmal eine Musik nur im innern Ohr reproduzieren kann, aber sie nicht pfeifen, weil das Pfeifen schon die innere Stimme übertönt, so ist manchmal die Stimme eines philosophischen Gedankens so leise, daß sie vom Lärm des gesprochenen Wortes schon übertönt wird und nicht mehr gehört werden kann, wenn man gefragt wird und reden soll.)
454. Plato: "—Wie? sagt er, die sollte nicht nutzen? Denn wenn doch einmal die Besonnenheit die Erkenntnis der Erkenntnisse ist und den andern Erkenntnissen vorsteht, so muß sie ja auch dieser sich auf das Gute beziehenden Erkenntnis vorstehen und uns so doch nutzen.—Macht auch sie uns, sprach ich, etwa gesund und nicht die Heilkunde? Und so auch mit den andern Künsten; verrichtet sie die Geschäfte derselben und nicht viel mehr jede von ihnen das ihrige? Oder haben wir nicht lange schon eingestanden, daß sie nur der Erkenntnisse und Unkenntnisse Erkenntnis wäre und keiner anderen Sache?—Allerdings wohl.—Sie also wird uns nicht die Gesundheit bewirken?—Wohl nicht.—Weil nämlich die Gesundheit für eine andere Kunst gehört?—Ja.—Also auch nicht den Nutzen, Freund, wird sie uns bewirken. Denn auch dieses Geschäft haben wir jetzt einer andern Kunst beigelegt.—Freilich.—Wie kann also die Besonnenheit nützlich sein, wenn sie uns gar keinen Nutzen bringt?"
455. (Der Philosoph ist nicht Bürger einer Denkgemeinde. Das ist, was ihn zum Philosophen macht.)
456. Manche Philosophen (oder wie man sie nennen soll) leiden an dem, was man "loss of problems", "Problemverlust" nennen kann. Es scheint ihnen dann alles ganz einfach, und es scheinen keine tiefen Probleme mehr zu existieren, die Welt wird weit und flach und verliert jede Tiefe, und was sie schreiben, wird unendlich seicht und trivial. Russell und H. G. Wells haben dieses Leiden.
457. .... quia plus loquitur inquisitio quam inventio .... (Augustinus.)
458. Philosophische Untersuchungen: begriffliche Untersuchungen. Das Wesentliche der Metaphysik: daß sie den Unterschied zwischen sachlichen und begrifflichen Untersuchungen verwischt.
459. Das Fundamentale grammatisch ausgedrückt: Wie ist es mit dem Satz "man kann nicht zweimal in den gleichen Fluß steigen"?
460. Man kann in gewissem Sinn mit philosophischen Irrtümern nicht vorsichtig genug umgehen, sie enthalten so viel Wahrheit.
461. Ich möchte doch, daß du sagst: "Ja, es ist wahr, das könnte man sich denken, das konnte auch geschehen!" Aber wollte ich dich darauf aufmerksam machen, daß du imstande bist, dir dies vorzustellen?——Ich wollte dies Bild vor deine Augen stellen, und deine Anerkennung dieses Bildes besteht darin, daß du nun geneigt bist, einen gegebenen Fall anders zu betrachten: nämlich ihn mit dieser Bilderreihe zu vergleichen. Ich habe deine Anschauungsweise geändert. (Ich habe irgendwo gelesen, daß gewissen indischen Mathematikern zum Beweis eines Satzes eine geometrische Figur dient mit den Worten: "Sieh' dies an!" Auch dies Ansehen bewirkt eine Änderung der Anschauungsweise.)
462. (Die Klassifikationen der Philosophen und Psychologen: sie klassifizieren Wolken nach ihrer Gestalt.)
463. Zur Mathematik: "Du hast einen falschen Begriff.—Aber aufklären läßt sich die Sache nicht dadurch, daß ich gegen deine Worte wettere; sondern nur dadurch, daß ich versuche, deine Aufmerksamkeit von gewissen Ausdrücken, Illustrationen, Vorstellungen weg und auf die Verwendung der Wörter hin zu lenken."
464. Der Stammbaum der psychologischen Phänomene: Nicht Exaktheit strebe ich an, sondern Übersichtlichkeit.
465. Die Behandlung aller dieser Erscheinungen des Seelenlebens ist mir nicht darum wichtig, weil es mir auf Vollständigkeit ankommt. Sondern, weil jede für mich auf die richtige Behandlung aller ein Licht wirft.
466. Und nicht um Symptome handelt es sich hier, sondern um logische Kriterien. Daß diese nicht immer scharf getrennt sind, hindert nicht, daß sie getrennt sind.
467. Unsere Untersuchung trachtet nicht, die eigentliche, exakte Bedeutung der Wörter zu finden; wohl aber geben wir den Wörtern im Verlauf unsrer Untersuchung oft exakte Bedeutungen.
468. "Der Mensch denkt, fürchtet sich, etc. etc.": das könnte man etwa einem antworten, der gefragt hat, welche Kapitel ein Buch über Psychologie enthalten soll.
469. Denke, jemand sagt: "Der Mensch hofft." Wie hätte man dies allgemeine naturgeschichtliche Phänomen zu beschreiben?—Man könnte ein Kind beobachten und warten, bis es eines Tages Hoffnung äußert; und man könnte dann sagen: "Heute hat es zum ersten Mal gehofft". Aber das klingt doch seltsam! Obwohl es ganz natürlich wäre zu sagen "Heute hat es zum ersten Mal gesagt 'ich hoffe'". Und warum seltsam?—Man sagt doch nicht von einem Säugling, er hoffe ...., noch auch, er hoffe nicht...., und man sagt es doch vom Erwachsenen.—Nun, das tägliche Leben wird nach und nach zu dem, worin für Hoffnung Platz ist.
Aber nun sagt man: Man kann eben nicht sicher sein, wann das Kind wirklich anfängt zu hoffen, denn Hoffnung ist ein innerer Vorgang. Welcher Unsinn! Wie weiß man denn dann überhaupt, wovon man redet?
470. Oder könnte er so exemplifizieren: "Ich, z.B., sehe, bin nicht blind"? Auch das klingt sonderbar.
Es wäre richtig zu sagen: "Und auch an mir kannst du die Erscheinung des Denkens, Hoffens, Sehens etc. beobachten."
471. Die psychologischen Verben sehen, glauben, denken, wünschen bezeichnen nicht Erscheinungen. Aber die Psychologie beobachtet die Erscheinungen des Sehens, Glaubens, Denkens, Wünschens.
472. Plan zur Behandlung der psychologischen Begriffe.
Psychologische Verben charakterisiert dadurch, daß die Person des Präsens durch Beobachtung zu verifizieren ist, die erste Person nicht.
Satz in der dritten Person des Präsens: Mitteilung. In der ersten Person Präsens: Äußerung. ((Stimmt nicht ganz.))
Die erste Person des Präsens der Äußerung verwandt.
Sinnesempfindungen: ihre inneren Zusammenhänge und Analogien.
Alle haben echte Dauer. Möglichkeit der Angabe des Anfangs und Endes. Möglichkeit der Gleichzeitigkeit, des zeitlichen Zusammenfallens.
Alle haben Grade und qualitative Mischungen. Grad: kaum merkbar—nicht auszuhalten.
In diesem Sinne gibt es nicht Lage- oder Bewegungsempfindung. Ort der Empfindung am Leib: unterscheidet Sehen und Hören von Druck-, Temperatur-, Geschmacks- und Schmerzempfindung.
473. Man muß daran denken, daß es einen Zustand der Sprache geben kann (und wohl gegeben hat), in welchem sie den allgemeinen Begriff der Sinnesempfindung nicht besitzt, aber doch Wörter, die unseren "sehen", "hören", "schmecken" entsprechen.
474. Sinneswahrnehmungen nennen wir Sehen, Hören, ..... Zwischen diesen Begriffen bestehen Analogien und Zusammenhänge; sie sind unsere Rechtfertigung für diese Zusammenfassung.
475. Man kann also fragen: Was für Zusammenhänge und Analogien bestehen zwischen Sehen und Hören? Zwischen Sehen und Greifen? Zwischen Sehen und Riechen? Etc.
476. Und fragt man das, so rücken die Sinne für uns gleich weiter auseinander, als sie auf den ersten Blick zu liegen schienen.
477. Was ist den Sinneserlebnissen gemeinsam?—Die Antwort, daß sie uns die Außenwelt kennen lehren, ist eine falsche und eine richtige. Sie ist richtig, sofern sie auf ein logisches Kriterium deuten soll.
478. Die Dauer der Empfindung. Vergleiche die Dauer einer Tonempfindung mit der Dauer der Tastempfindung, die dich lehrt, daß du eine Kugel in der Hand hältst; und mit dem "Gefühl", das dich lehrt, daß deine Kniee gebogen sind.
479. Wir fühlen unsere Bewegungen. Ja, wir fühlen sie wirklich; die Empfindung ist nicht ähnlich einer Geschmacksempfindung oder einer Hitzeempfindung, sondern einer Tastempfindung: der Empfindung, wenn Haut und Muskeln gedrückt, gezogen, verschoben werden.
480. Ich fühle meinen Arm und seltsamerweise möchte ich nun sagen: ich fühle ihn im Raum in bestimmter Lage; als wäre nämlich das Körpergefühl in einem Raum in der Form des Arms verteilt, sodaß ich, um es darzustellen, den Arm etwa in Gips in seiner richtigen Lage darstellen müßte.
481. Ja, es ist seltsam. Mein Unterarm liegt jetzt horizontal, und ich möchte sagen, daß ich das fühle; aber nicht so, als hätte ich ein Gefühl, das immer mit dieser Lage zusammengeht (als fühlte man etwa Blutleere oder Plethora)—sondern, als wäre eben das 'Körpergefühl' des Arms horizontal angeordnet oder verteilt, wie etwa ein Dunst oder Staubteilchen an der Oberfläche meines Armes so im Raume verteilt sind. Es ist also nicht wirklich, als fühlte ich die Lage meines Arms, sondern als fühlte ich meinen Arm, und das Gefühl hätte die und die Lage. D. h. aber nur: ich weiß einfach, wie er liegt—ohne es zu wissen, weil .... Wie ich auch weiß, wo ich den Schmerz empfinde—es aber nicht weiß, weil ....
482. Es ist uns förmlich, als hätte der Schmerz einen Körper, als wäre er ein Ding, ein Körper mit Form und Farbe. Warum? Hat er die Form des schmerzenden Körperteils? Man möchte z. B. sagen: "Ich könnte den Schmerz beschreiben, wenn ich nur die nötigen Worte und Elementarbedeutungen dazu hätte." Man fühlt: es fehlt einem nur die notwendige Nomenklatur. (James.) Als könnte man die Empfindung sogar malen, wenn nur der Andere diese Sprache verstünde.—Und man kann den Schmerz ja wirklich räumlich und zeitlich beschreiben.
483. (Wenn Empfindungen die Lage der Glieder und die Bewegungen charakterisieren, so ist ihr Ort jedenfalls nicht das Gelenk.)
Die Lage der Glieder und ihre Bewegungen weiß man. Man kann sie z. B. angeben, wenn man gefragt wird. So wie man auch den Ort einer Empfindung (Schmerz) am Leibe weiß.
Reaktion des Berührens der schmerzhaften Stelle.
Kein lokales Merkmal an der Empfindung. So wenig wie ein Zeitliches am Erinnerungsbild. (Zeitliche Merkmale an der Photographie.)
Schmerz von andern Sinnesempfindungen unterschieden durch charakteristischen Ausdruck. Dadurch verwandt der Freude (die keine Sinnesempfindung).
484. Ist das Wortklauberei:—Freude, Genuß, Entzücken seien nicht Empfindungen?—Fragen wir uns einmal: Wieviel Analogie besteht denn zwischen dem Entzücken und dem, was wir z. B. "Sinnesempfindungen" nennen?
485. Das Bindeglied zwischen ihnen wäre der Schmerz. Denn sein Begriff ähnelt dem der Tastempfindung, z. B. (durch die Merkmale der Lokalisierung, echten Dauer, Intensität, Qualität) und zugleich dem der Gemütsbewegungen durch den Ausdruck (Mienen, Gebärden, Laute).
486. "Ich fühle große Freude."—Wo?—Das klingt unsinnig. Und doch sagt man auch "Ich fühle eine freudige Erregung in meiner Brust."—Warum aber ist Freude nicht lokalisiert? Ist es, weil sie über den ganzen Körper verteilt ist? Auch dann ist sie nicht lokalisiert, wenn etwa das Gefühl, das sie hervorruft, dies ist; wenn wir uns etwa am Geruch einer Blume freuen. Die Freude äußert sich im Gesichtsausdruck, im Benehmen. (Aber wir sagen nicht, wir freuten uns im Gesicht.)
487. "Aber ich habe doch ein wirkliches Gefühl der Freude!" Ja, wenn du dich freust, so freust du dich wirklich. Und freilich ist Freude nicht freudiges Benehmen, noch auch ein Gefühl um die Mundwinkel und Augen.
"Aber 'Freude' bezeichnet doch etwas Inneres." Nein. "Freude" bezeichnet gar nichts. Weder Inneres noch Äußeres.
488. Fortsetzung der Klassifizierung der psychologischen Begriffe.
Gemütsbewegungen. Ihnen gemeinsam echte Dauer, ein Verlauf. (Zorn flammt auf, läßt nach, verschwindet; ebenso: Freude, Depression, Furcht.)
Unterschied von den Empfindungen: sie sind nicht lokalisiert (auch nicht diffus!).
Gemeinsam: sie haben ein charakteristisches Ausdrucksbenehmen. (Gesichtsausdruck.) Und daraus folgt schon: auch charakteristische Empfindungen. So geht die Trauer oft mit dem Weinen einher, und mit ihm, charakteristische Empfindungen. (Die tränenschwere Stimme.) Aber diese Empfindungen sind nicht die Gemütsbewegungen. (In dem Sinne, wie die Ziffer 2 nicht die Zahl 2 ist.)
Unter den Gemütsbewegungen könnte man gerichtete von ungerichteten unterscheiden. Furcht vor etwas, Freude über etwas.
Dies Etwas ist das Objekt, nicht die Ursache der Gemütsbewegung.
489. Das Sprachspiel "Ich fürchte mich" enthält schon das Objekt.
Angst könnte man ungerichtete Furcht nennen, insofern ihre Äußerungen ähnlich oder gleich denen der Furcht sind.
Der Inhalt einer Gemütsbewegung—darunter stellt man sich so etwas vor wie ein Bild oder etwas, wovon ein Bild gemacht werden kann. (Die Finsternis der Depression, die sich auf einen herniedersenkt, die Flamme des Zornes.)
490. Man könnte auch das menschliche Gesicht ein solches Bild nennen und den Verlauf der Leidenschaft durch seine Veränderungen darstellen.
491. Zum Unterschied von den Empfindungen: sie unterrichten uns nicht über die Außenwelt. (Grammatische Bemerkung.)
Liebe und Haß könnte man Gemütsdispositionen nennen: auch Furcht in einem bestimmten Sinne.
492. Es ist eines, akute Furcht empfinden, und ein Anderes, jemanden 'chronisch' fürchten. Aber Furcht ist keine Empfindung.
'Schreckliche Furcht': sind es die Empfindungen, die so schrecklich sind?
Typische Ursachen des Schmerzes einerseits, der Depression, Trauer, Freude anderseits. Ursache dieser zugleich ihr Objekt.
Das Benehmen des Schmerzes und das Benehmen der Traurigkeit.—Man kann diese nur mit ihren äußeren Anlässen beschreiben. (Wenn die Mutter das Kind allein läßt, mag es vor Trauer weinen; wenn es hinfällt, vor Schmerz.) Benehmen und Art des Anlasses gehören zusammen.
493. Es gibt furchtvolle Gedanken, hoffnungsvolle, freudige, zornige, etc.
494. Gemütsbewegungen drücken sich in Gedanken aus. Einer redet zornig, furchtsam, traurig, freudig, etc., nicht kreuzschmerzlịch.
Ein Gedanke flößt mir Gemütsbewegungen (Furcht, Trauer etc.) ein, nicht Körperschmerz.
495. Fast möchte ich sagen: Man fühlt die Trauer so wenig im Körper, wie das Sehen im Auge.
496. (Das Schreckliche an der Furcht sind nicht die Furchtempfindungen.) Diese Sache erinnert auch an das Hören eines Geräusches aus einer bestimmten Richtung. Es ist beinahe, als fühlte man die Beschwerde in der Magengegend, Beklemmung des Atems, aus der Richtung der Furcht. D. h. eigentlich, daß "Mir ist schlecht vor Furcht" nicht eine Ursache der Furcht angibt.
497. "Wo spürst du den Kummer?"—In der Seele.——Was für Konsequenzen ziehen wir aus dieser Ortsangabe? Eine ist, daß wir nicht von einem körperlichen Ort des Kummers reden. Aber wir deuten doch auf unsern Leib, als wäre der Kummer in ihm. Ist das, weil wir ein körperliches Unbehagen spüren? Ich weiß die Ursache nicht. Aber warum soll ich annehmen, sie sei ein leibliches Unbehagen?
498. Denke dir folgende Frage: Kann man sich einen Schmerz, sagen wir von der Qualität des rheumatischen Schmerzes, denken, aber ohne Örtlichkeit? Kann man sich ihn vorstellen?
Wenn du anfängst, darüber nachzudenken, so siehst du, wie sehr du das Wissen um den Ort des Schmerzes in ein Merkmal des Gefühlten verwandeln möchtest, in ein Merkmal eines Sinnesdatums, des privaten Objekts, das vor meiner Seele steht.
499. Wenn die Angst furchtbar ist, und wenn ich in ihr mir meiner Atmung bewußt bin und einer Spannung in meinen Gesichtsmuskeln,—sagt das, daß diese Gefühle mir furchtbar sind? Könnten sie nicht sogar eine Linderung bedeuten? (Dostojewski.)
500. Warum verwendet man aber das Wort "leiden" für die Furcht und auch für den Schmerz? Nun, es sind ja Verbindungen genug.—
501. Auf die Äußerung "Ich kann nicht ohne Furcht daran denken ...." antwortet man etwa: "Es ist kein Grund zur Furcht, denn ...." Das ist jedenfalls ein Mittel, Furcht zu beseitigen. Gegensatz zum Schmerz.
502. Daß es ein Furchtkonglomerat von Empfindungen, Gedanken etc. (z. B.) gibt, heißt nicht, daß Furcht ein Konglomerat (Syndrom) ist.
503. Wer im Studierzimmer sich die Trauer vormacht, der wird sich allerdings leicht der Spannungen in seinem Gesicht bewußt werden. Aber trauere wirklich, oder folge einer traurigen Handlung im Film, und frage dich, ob du dir deines Gesichts bewußt warst.
504. Liebe ist kein Gefühl. Liebe wird erprobt, Schmerzen nicht. Man sagt nicht: "Das war kein wahrer Schmerz, sonst hätte er nicht so schnell nachgelassen".
505. Ein Zusammenhang zwischen den Stimmungen und Sinneseindrücken ist, daß wir die Stimmungsbegriffe zur Beschreibung von Sinneseindrücken und Vorstellungen benützen. Wir sagen von einem Thema, einer Landschaft, sie seien traurig, fröhlich, etc. Aber viel wichtiger ist es natürlich, daß wir das menschliche Gesicht, die Handlung, das Benehmen durch alle Stimmungsbegriffe beschreiben.
506. Ein freundlicher Mund, ein freundliches Auge. Wie denkt man sich eine freundliche Hand?—Wahrscheinlich geöffnet und nicht als Faust.—Und könnte man sich die Haarfarbe des Menschen als Ausdruck der Freundlichkeit oder des Gegenteils denken?—Aber so gestellt, scheint dies die Frage zu sein, ob uns das gelingen kann. Die Frage sollte lauten: Wollen wir etwas eine freundliche oder unfreundliche Haarfarbe nennen? Wollten wir solchen Worten Sinn geben, so würden wir uns etwa einen Menschen denken, dessen Haare dunkel werden, wenn er zornig wird. Das Hineinlesen des bösen Ausdrucks in die dunkeln Haare aber geschähe mittels einer schon früher fertigen Idee.
Man kann sagen: Das freundliche Auge, der freundliche Mund, das Wedeln des Hundes sind, unter andern, primäre und von einander unabhängige Symbole der Freundlichkeit; ich meine: sie sind Teile der Phänomene, die man Freundlichkeit nennt. Will man sich andere Erscheinungen als Ausdruck der Freundlichkeit denken, so sieht man jene Symbole in sie hinein. Wir sagen "Er macht ein finsteres Gesicht"; vielleicht, weil die Augen durch die Augenbrauen stärker beschattet werden; und nun übertragen wir die Idee der Finsternis auf die Haarfarbe.
507. Wer fragt, ob Vergnügen eine Empfindung ist, unterscheidet wahrscheinlich nicht zwischen Grund und Ursache, denn sonst fiele ihm auf, daß man an etwas Vergnügen hat, was nicht heißt, daß dies Etwas eine Empfindung in uns verursacht.
508. Aber Vergnügen geht doch jedenfalls mit einem Gesichtsausdruck zusammen, und den sehen wir zwar nicht an uns selbst, aber spüren ihn doch.
Und versuch einmal über etwas sehr Trauriges nachzudenken mit dem Gesichtsausdruck strahlender Freude!
509. Es ist ja möglich, daß die Drüsen des Traurigen anders sezernieren, als die des Fröhlichen; auch, daß diese Sekretion die oder eine Ursache der Trauer ist. Aber folgt daraus, daß die Trauer eine durch diese Sekretion hervorgerufene Empfindung ist?
510. Aber der Gedanke ist hier: "Du fühlst doch die Trauer——also mußt du sie irgendwo fühlen; sonst wäre sie eine Chimäre." Aber wenn du so denken willst, rufe dir die Verschiedenheit von Sehen und Schmerz ins Gedächtnis. Ich fühle den Schmerz in der Wunde——aber die Farbe im Auge? So wie wir hier ein Schema verwenden wollen, statt bloß das wirklich Gemeinsame zu notieren, sehen wir alles falsch vereinfacht.
511. Wollte man aber ein Analogon zum Ort des Schmerzes finden, so wäre es natürlich nicht die Seele (wie ja der Ort des Körperschmerzes nicht der Körper ist), sondern der Gegenstand der Reue.
512. Denke, man sagte: Fröhlichkeit wäre ein Gefühl, und Traurigkeit bestünde darin, daß man nicht fröhlich ist.—Ist denn die Abwesenheit eines Gefühls ein Gefühl?
513. Man spricht von einem Gefühl der Überzeugung, weil es einen Ton der Überzeugung gibt. Ja, das Charakteristikum aller 'Gefühle' ist, daß es einen Ausdruck, d. i. eine Miene, Gebärde des Gefühls gibt.
514. Nun könnte man aber so sagen: Das Gesicht eines Menschen ist durchaus nicht immer dieselbe Gestalt. Es ändert sich von Minute zu Minute; manchmal wenig, manchmal bis zur Unkenntlichkeit. Dennoch ist es möglich, das Bild seiner Physiognomie zu zeichnen. Freilich, ein Bild, auf dem das Gesicht lächelt, zeigt nicht, wie es weinend aussieht. Aber es läßt darauf immerhin Schlüsse zu.—Uns so wäre es auch möglich, eine Art ungefähre Physiognomie des Glaubens (z. B.) zu beschreiben.
515. Ich gebe Zeichen des Entzückens und des Verständnisses.
516. Kann man das 'sich auskennen' ein Erlebnis nennen? Nicht doch. Aber es gibt Erlebnisse charakteristisch für den Zustand des Sich-auskennens und des Sich-nicht-auskennens. (Sich nicht auskennen und lügen.)
517. Es ist aber doch wichtig, daß es alle diese Paraphrasen gibt! Daß man die Sorge mit den Worten beschreiben kann "Ewiges Düstere steigt herunter". Ich habe vielleicht die Wichtigkeit dieses Paraphrasierens nie genügend betont.
518. Warum kann der Hund Furcht, aber nicht Reue empfinden? Wäre es richtig zu sagen "Weil er nicht sprechen kann"?
519. Nur wer über die Vergangenheit nachdenken kann, kann bereuen. Das heißt aber nicht, daß nur so einer erfahrungsgemäß des Gefühls der Reue fähig ist.
520. Es ist ja auch nichts Erstaunliches, daß gewisse Begriffe nur auf ein Wesen anwendbar sein sollten, das z. B. eine Sprache besitzt.
521. "Der Hund meint etwas mit seinem Wedeln."—Wie würde man das begründen?—Sagt man auch: "Die Pflanze, wenn sie ihre Blätter hängen läßt, meint damit, daß sie Wasser braucht"?—
522. Wir würden kaum fragen, ob das Krokodil etwas damit meint, wenn es mit offenem Rachen auf einen Menschen zukommt. Und wir würden erklären: das Krokodil könne nicht denken, und darum sei eigentlich hier von einem Meinen keine Rede.
523. Vergessen wir doch einmal ganz, daß uns der Seelenzustand des Fürchtenden interessiert. Gewiß ist, daß uns auch sein Benehmen unter gewissen Umständen als Anzeichen für künftiges Verhalten interessieren kann. Warum sollten wir also nicht dafür ein Wort haben?
Man könnte nun fragen, ob dies Wort sich wirklich einfach auf das Benehmen, einfach auf die Veränderung des Körpers bezöge. Und das können wir verneinen. Es liegt uns ja nichts daran, den Gebrauch dieses Worts derart zu vereinfachen. Es bezieht sich auf das Benehmen unter gewissen äußeren Umständen. Wenn wir diese Umstände und jenes Benehmen beobachten, sagen wir, einer sei ...., oder habe .....
524. Es könnte einen Furchtbegriff geben, der nur auf Tiere, also nur durch Beobachtung, Anwendung fände.—Du willst doch nicht sagen, daß so ein Begriff keinen Nutzen hätte. Das Verbum, das beiläufig dem Wort "fürchten" entspräche, hätte dann keine erste Person, und keine seiner Formen wäre Äußerung der Furcht.
525. Ich will nun sagen, daß Menschen, welche einen solchen Begriff verwenden, seinen Gebrauch nicht müßten beschreiben können. Und sollten sie es versuchen, so wäre es möglich, sie gäben eine ganz unzulängliche Beschreibung. (Wie die meisten, wenn sie versuchen wollten, die Verwendung des Geldes richtig zu beschreiben.) (Sie sind auf so eine Aufgabe nicht gefaßt.)
526. Wer sich unter den und den Umständen so und so benimmt, von dem sagen wir, er sei traurig. (Auch vom Hunde.) Insofern kann man nicht sagen, das Benehmen sei die Ursache der Trauer; sie ist ihr Anzeichen. Sie die Wirkung der Trauer zu nennen, wäre auch nicht einwandfrei.—Sagt er es von sich (er sei traurig), so wird er im allgemeinen dafür als Grund nicht sein trauriges Gesicht u. dergl. angeben. Wie aber wäre es damit: "Erfahrung hat mich gelehrt, daß ich traurig werde, sobald ich anfange, traurig dazusitzen, etc."? Das könnte zweierlei besagen. Erstens: "Sobald ich, etwa einer leichten Neigung folgend, es mir gestatte, mich so und so zu halten und zu benehmen, gerate ich in den Zustand, in diesem Benehmen verharren zu müssen." Es könnte ja sein, daß Zahnschmerzen durch Stöhnen ärger würden.—Zweitens aber könnte jener Satz eine Spekulation enthalten über die Ursache der menschlichen Trauer; des Inhalts, daß, wer imstande wäre auf irgend eine Weise gewisse Körperzustände hervorzurufen, den Menschen traurig machen würde. Hier ist aber die Schwierigkeit, daß wir einen Menschen, der unter allen Umständen traurig aussähe und sich benähme, nicht traurig nennen würden. Ja, wenn wir einem solchen den Ausdruck "Ich bin traurig" beibrächten, und er sagte das stets und ständig mit dem Ausdruck der Trauer, so hätten diese Worte, so wie die übrigen Zeichen, ihren normalen Sinn verloren.
527. Ist es nicht so, als wollte man sich einen Gesichtsausdruck vorstellen, der nicht allmählicher, schwer faßbarer Veränderungen fähig wäre, sondern, sagen wir nur fünf Stellungen hätte; bei einer Veränderung ginge die eine mit einem Ruck in die andere über. Wäre nun dies starre Lächeln z. B. wirklich ein Lächeln? Und warum nicht?—"Lächeln" nennen wir eine Miene in einem normalen Mienenspiel.—Ich könnte mich vielleicht nicht so dazu verhalten, wie zu einem Lächeln. Es würde mich z. B. nicht selber zum Lächeln bringen. "Kein Wunder" will man sagen, "daß wir diesen Begriff haben unter diesen Umständen."
528. Eine Hilfskonstruktion. Ein Stamm, den wir versklaven wollen. Die Regierung und die Wissenschaft geben aus, daß die Leute dieses Stammes keine Seelen haben; man könne sie also zu jedem beliebigen Zweck gebrauchen. Natürlich interessiert uns dennoch ihre Sprache; denn wir wollen ihnen ja z. B. Befehle geben und Berichte von ihnen erhalten. Auch wollen wir wissen, was sie unter einander reden, da dies mit ihrem übrigen Verhalten zusammenhängt. Aber auch, was bei ihnen unsern 'psychologischen Äußerungen' entspricht, muß uns interessieren; denn wir wollen sie arbeitsfähig erhalten; darum sind uns ihre Äußerungen des Schmerzes, des Unwohlseins, der Niedergeschlagenheit, der Lebenslust etc., etc. von Wichtigkeit. Ja, wir haben auch gefunden, daß man diese Leute mit gutem Erfolg als Versuchsobjekte in physiologischen und psychologischen Laboratorien verwenden kann, da ihre Reaktionen—auch die Sprachreaktionen—ganz die der seelenbegabten Menschen sind. Man habe auch gefunden, daß man diesen Wesen durch eine Methode, die sehr ähnlich unserm 'Unterricht' ist, unsere Sprache statt der ihrigen beibringen kann.
529. Diese Wesen lernen nun z. B. rechnen, schriftlich oder mündlich rechnen. Wir bringen sie aber auf irgend eine Weise dahin, daß sie uns das Ergebnis einer Multiplikation sagen können, nachdem sie, ohne zu schreiben oder zu sprechen, sich eine Weile in 'nachdenkender' Haltung verhalten haben. Wenn man die Art und Weise betrachtet, wie sie dies 'Kopfrechnen' lernen und die Erscheinungen, die es umgeben, so liegt das Bild nahe, der Prozeß des Rechnens sei gleichsam untergetaucht und gehe nun unter der Wasserfläche vor sich.
Wir müssen natürlich für verschiedene Zwecke einen Befehl haben der Art "Rechne dies im Kopf!"; eine Frage "Hast du es gerechnet?"; ja auch: "Wie weit bist du?"; eine Aussage des Automaten "Ich habe .... gerechnet"; etc. Kurz: alles, was wir unter uns über das Kopfrechnen sagen, hat auch Interesse für uns, wenn sie es sagen. Und was für Kopfrechnen gilt, gilt auch für alle anderen Formen des Denkens.——Äußert einer von uns die Meinung, diese Wesen müßten doch irgendeine Art von Seele haben, in der dies und jenes vor sich ginge, so lachen wir ihn aus.
530. Die Sklaven sagen auch: "Als ich das Wort 'Bank' hörte, bedeutete es für mich .....". Frage: Auf dem Hintergrund welcher Sprachtechnik sagen sie das? Denn darauf kommt alles an. Was hatten wir sie gelehrt, welche Benutzung des Wortes "bedeuten"? Und was, wenn überhaupt irgend etwas, entnehmen wir ihrer Äußerung? Denn wenn wir gar nichts mit ihr anfangen können, so könnte sie uns als Kuriosität interessieren.——Denken wir uns einen Stamm von Menschen, die keine Träume kennen, und die unsere Traumerzählungen hören. Einer von uns käme zu diesen nichtträumenden Leuten und lernte nach und nach, sich mit ihnen zu verständigen.—Vielleicht denkt man, sie würden nun das Wort "träumen" nie verstehen. Aber sie würden bald eine Verwendung dafür finden. Und ihre Ärzte könnten sich sehr wohl für das Phänomen interessieren und wichtige Schlüsse aus den Träumen des Fremden ziehen.——Auch kann man nicht sagen, daß für diese Leute das Verbum "träumen" nichts Anderes bedeuten könnte als: einen Traum erzählen. Denn der Fremde würde ja beide Ausdrücke gebrauchen: "träumen" und "einen Traum erzählen", und die Leute jenes Stammes dürften nicht "ich träumte ..." mit "ich erzählte den Traum ....." verwechseln.
531. "Ich nehme an, es schwebe ihm ein Bild vor."—Könnte ich auch annehmen, es schwebe diesem Ofen ein Bild vor?—Und warum scheint dies unmöglich? Ist denn also die menschliche Gestalt dazu nötig?—
532. Der Schmerzbegriff ist charakterisiert durch seine bestimmte Funktion in unserm Leben.
533. Schmerz liegt so in unserm Leben drin, hat solche Zusammenhänge. (D. h.: nur was so im Leben drinliegt, solche Zusammenhänge hat, nennen wir "Schmerz".)
534. Nur inmitten gewisser normaler Lebensäußerungen gibt es eine Schmerzäußerung. Nur inmitten von noch viel weitgehender bestimmter Lebensäußerung den Ausdruck der Trauer oder der Zuneigung. U. s. f.
535. Wenn ich mir, und wenn ein Andrer sich einen Schmerz vorstellen kann, oder wir doch sagen, daß wir es können,—wie kann man herausfinden, ob wir ihn uns richtig vorstellen, und wie genau?
536. Ich mag wissen, daß er Schmerzen hat, aber ich weiß nie den genauen Grad seiner Schmerzen. Hier ist also etwas, was er weiß und die Schmerzäußerung mir nicht mitteilt. Etwas rein Privates.
Er weiß genau, wie stark seine Schmerzen sind? (Ist das nicht ähnlich, als sagte man, er wisse immer genau, wo er sich befinde? Nämlich hier.) Ist denn der Begriff des Grades mit den Schmerzen gegeben?
537. Du sagst, du pflegst den Stöhnenden, weil Erfahrung dich gelehrt hat, daß du selbst stöhnst, wenn du das und das fühlst. Aber da du ja doch keinen solchen Schluß ziehst, so können wir die Begründung durch Analogie weglassen.
538. Es hat auch keinen Sinn zu sagen: "Ich kümmere mich nicht um mein eigenes Stöhnen, weil ich weiß, daß ich Schmerzen habe" oder "weil ich meine Schmerzen fühle."
Wohl aber ist es wahr:—"Ich kümmere mich nicht um mein Stöhnen."
539. Ich schließe aus der Beobachtung seines Benehmens, daß er zum Arzt muß; aber ich ziehe diesen Schluß für mich nicht aus der Beobachtung meines Benehmens. Oder vielmehr: ich tue auch dies manchmal, aber nicht in analogen Fällen.
540. Es hilft hier, wenn man bedenkt, daß es ein primitives Verhalten ist, die schmerzende Stelle des Andern zu pflegen, zu behandeln, und nicht nur die eigene—also auf des Andern Schmerzbenehmen zu achten, wie auch, auf das eigene Schmerzbenehmen nicht zu achten.
541. Was aber will hier das Wort "primitiv" sagen? Doch wohl, daß die Verhaltungsweise vorsprachlich ist: daß ein Sprachspiel auf ihr beruht, daß sie das Prototyp einer Denkweise ist und nicht das Ergebnis des Denkens.
542. "Falsch aufgezäumt" kann man von einer Erklärung sagen, wie dieser: Wir pflegten den Andern, weil wir nach Analogie des eigenen Falles glaubten, auch er habe ein Schmerzerlebnis.—Statt zu sagen: Lerne also aus diesem besondern Kapitel des menschlichen Benehmens—aus dieser Sprachverwendung—eine neue Seite.
543. Zu meinem Begriff gehört hier mein Verhältnis zur Erscheinung.
544. Wenn wir dem Arzt mitteilen, wir hätten Schmerzen—in welchen Fällen ist es nützlich, daß er sich einen Schmerz vorstelle?—Und geschieht dies nicht auf sehr mannigfache Weise? (So mannigfach, wie sich an einen Schmerz erinnern.) (Wissen, wie ein Mensch ausschaut.)
545. Angenommen, es erklärt einer, wie ein Kind den Gebrauch des Wortes "Schmerz" lernt, in dieser Weise: Wenn das Kind sich bei bestimmten Anlässen so und so benimmt, denke ich, es fühle, was ich in solchen Fällen fühle; und wenn es so ist, so assoziiert das Kind das Wort mit seinem Gefühl und gebraucht das Wort, wenn das Gefühl wieder auftritt.——Was erklärt diese Erklärung? Frage dich: Welche Art der Unwissenheit behebt sie?-Sicher sein, daß der Andre Schmerzen hat, zweifeln, ob er sie hat, u. s. f., sind soviele natürliche instinktive Arten des Verhältnisses zu den andern Menschen, und unsre Sprache ist nur ein Hilfsmittel und weiterer Ausbau dieses Verhaltens. Unser Sprachspiel ist ein Ausbau des primitiven Benehmens. (Denn unser Sprachspiel ist Benehmen.) (Instinkt.)
546. "Ich bin nicht sicher, ob er Schmerzen hat."—Wenn sich nun einer immer, wenn er dies sagt, mit einer Nadel stäche, um die Bedeutung des Wortes "Schmerz" lebhaft vor der Seele zu haben, (um sich nicht mit der Vorstellung begnügen zu müssen) und zu wissen, worüber er beim Andern im Zweifel ist!—Wäre nun der Sinn seiner Aussage gesichert?
547. Er hat also den wahren Schmerz; und der Besitz dieses ist es, was er beim Andern bezweifelt.—Aber wie macht er das nur?——Es ist, als sagte man mir: "Hier hast du einen Sessel. Siehst du ihn genau?—Gut—nun übertrage ihn ins Französische!"
548. Er hat also den wirklichen Schmerz, und nun weiß er, was er beim Andern bezweifeln soll. Er hat den Gegenstand vor sich, und es ist kein 'Benehmen' oder dergleichen. (Aber jetzt!) Zum Bezweifeln, ob der Andre Schmerzen hat, braucht er den Begriff 'Schmerz', nicht Schmerzen.
549. Die Äußerung der Empfindung eine Behauptung zu nennen, ist dadurch irreführend, daß mit dem Wort "Behauptung" die 'Prüfung', die 'Begründung', die 'Bestätigung', die 'Entkräftung' der Behauptung im Sprachspiel verbunden ist.
550. Wozu dient etwa die Aussage: "Ich habe doch etwas, wenn ich Schmerzen habe"?
551. "Der Geruch ist herrlich!" Ist ein Zweifel darüber, daß der Geruch es ist, der herrlich ist?
So ist es eine Eigenschaft des Geruches?—Warum nicht? Es ist eine Eigenschaft der Zehn, durch zwei teilbar zu sein und auch, die Zahl meiner Finger zu sein.
Es könnte aber eine Sprache geben, in der die Leute nur die Augen schließen und sagen "Oh, dieser Geruch!" und es keinen Subjekt-Prädikat-Satz gibt, der dem äquivalent ist. Das ist eben eine 'spezifische' Reaktion.
552. Zu dem Sprachspiel mit den Worten "er hat Schmerzen" gehört—möchte man sagen—nicht nur das Bild des Benehmens, sondern auch das Bild des Schmerzes.—Aber hier muß man sich in Acht nehmen: Denke an mein Beispiel von den privaten Tabellen, die nicht zum Spiel gehören.—Es entsteht der Eindruck der 'privaten Tabelle' im Spiel durch die Abwesenheit einer Tabelle und durch die Ähnlichkeit des Spiels mit einem solchen, das mit einer Tabelle gespielt wird.
553. Bedenke: Wir gebrauchen das Wort "Ich weiß nicht" oft in seltsamer Weise; wenn wir z. B. sagen, wir wissen nicht, ob dieser wirklich mehr fühlt als der Andere, oder es nur stärker zum Ausdruck bringt. Es ist dann nicht klar, welche Art der Untersuchung die Frage entscheiden könnte. Natürlich ist die Äußerung nicht ganz müßig: Wir wollen sagen, daß wir wohl die Gefühle des A und des B miteinander vergleichen können, aber uns die Umstände an einem Vergleich des A mit dem C irre werden lassen.
554. Nicht darauf sehen wir, daß die Evidenz das Gefühl (also das Innere) des Andern nur wahrscheinlich macht, sondern darauf, daß wir dies als Evidenz für irgend etwas Wichtiges betrachten, daß wir auf diese verwickelte Art der Evidenz ein Urteil gründen, daß sie also in unserm Leben eine besondere Wichtigkeit hat und durch einen Begriff herausgehoben wird. (Das Innere und 'Äußere', ein Bild.)
555. Die 'Unsicherheit' bezieht sich eben nicht auf den besondern Fall, sondern auf die Methode, auf die Regeln der Evidenz.
556. Die Unsicherheit hat ihren Grund nicht darin, daß er seine Schmerzen nicht außen am Rock trägt. Und es ist auch gar keine Unsicherheit in jedem besonders Fall. Wenn die Grenze zwischen zwei Ländern strittig wäre, würde daraus folgen, daß die Landesangehörigkeit jedes einzelnen Bewohners fraglich wäre?
557. Denke, Leute könnten das Funktionieren des Nervensystems im Andern beobachten. Sie unterschieden dann echte und geheuchelte Empfindung in sicherer Weise.—Oder könnten sie doch wieder daran zweifeln, daß der Andere bei diesen Zeichen etwas spürt?—Man könnte sich jedenfalls leicht vorstellen, daß, was sie da sehen, ihr Verhalten ohne alle Skrupel bestimmt.
Und nun kann man dies doch auf das äußere Benehmen übertragen.
Diese Beobachtung bestimmt ihr Verhalten gegen den Andern vollkommen und ein Zweifel kommt nicht auf.
558. Es gibt wohl den Fall, daß einer mir später sein Innerstes durch ein Geständnis aufschließt: aber, daß es so ist, kann mir nicht das Wesen von Außen und Innen erklären, denn ich muß ja dem Geständnis doch Glauben schenken.
Das Geständnis ist ja auch etwas Äußeres.
559. Besieh dir Leute, die auch unter diesen Umständen zweifeln; und solche, die nicht zweifeln.
560. Nur Gott sieht die geheimsten Gedanken. Aber warum sollen diese so wichtig sein? Manche sind wichtig, nicht alle. Und müssen alle Menschen sie für wichtig halten?
561. Eine Art der Unsicherheit wäre die, die wir auch einem uns unbekannten Mechanismus entgegenbringen könnten. Bei der andern würden wir uns möglicherweise an eine Begebenheit in unserm Leben erinnern. Es könnte z. B. sein, daß einer, der gerade der Todesangst entronnen ist, sich davor scheuen würde, eine Fliege zu erschlagen und es sonst ohne Bedenken täte. Oder anderseits, daß er mit diesem Erlebnis vor Augen, das zögernd tut, was er sonst ohne Zögern täte.
562. Auch wenn ich 'nicht sicher in meinem Mitleid ruhe', muß ich nicht an die Ungewißheit seines spätern Benehmens denken.
563. Die eine Unsicherheit geht sozusagen von dir aus, die andere von ihm.
Von der einen könnte man also doch sagen, sie hinge mit einer Analogie zusammen, von der Andern nicht. Aber nicht, als ob ich aus der Analogie einen Schluß zöge!
564. Wenn ich aber zweifle, ob eine Spinne wohl Schmerz empfindet, dann ist es nicht, weil ich nicht weiß, was ich mir zu erwarten habe.
565. Wir können aber nicht umhin, uns das Bild vom seelischen Vorgang zu machen. Und nicht, weil wir ihn von uns her kennen!
566. Könnte nicht das Verhalten, Benehmen des Vertrauens ganz allgemein unter einer Gruppe von Menschen bestehen? So daß ihnen ein Zweifel an Gefühlsäußerungen ganz fremd ist?
567. Wie könnte man die menschliche Handlungsweise beschreiben? Doch nur, insofern man die Handlungen der verschiedenen Menschen, wie sie durcheinanderwimmeln, schilderte. Nicht, was einer jetzt tut, eine einzelne Handlung, sondern das ganze Gewimmel der menschlichen Handlungen, der Hintergrund, worauf wir jede Handlung sehen, bestimmt unser Urteil, unsere Begriffe und Reaktionen.
568. Wenn das Leben ein Teppich wäre, so ist dies Muster (der Verstellung z. B.) nicht immer vollständig und vielfach variiert. Aber wir, in unserer Begriffswelt, sehen immer wieder das Gleiche mit Variationen wiederkehren. So fassen es unsere Begriffe auf. Die Begriffe sind ja nicht für einmaligen Gebrauch.
569. Und ein Muster ist im Teppich mit vielen andern Mustern verwoben.
570. "So kann man sich nicht verstellen."—Und das kann eine Erfahrung sein,—daß nämlich niemand, der sich so benimmt, sich später so und so benehmen werde; aber auch eine begriffliche Feststellung ("Das wäre nicht mehr Verstellung"); und die beiden können zusammenhängen.
Das kann man nicht mehr "Verstellung" nennen.
(Denn man hätte nicht gesagt, die Planeten müssen sich in Kreisen bewegen, wenn es nicht geschienen hätte, daß sie sich in Kreisen bewegen.)
(Vergleiche: "So kann man nicht reden ohne zu denken", "So kann man nicht unwillkürlich handeln.")
571. "Könntest du dir nicht eine weitere Umgebung denken, in der auch das noch als Verstellung zu deuten wäre?" Muß nicht jedes Benehmen sich so deuten lassen?
Aber was heißt es: daß alles Benehmen noch immer Verstellung sein könnte? Hat denn Erfahrung uns das gelehrt? Und wie können wir anders über Verstellung unterrichtet sein? Nein es ist eine Bemerkung über den Begriff 'Verstellung'. Aber da wäre ja dieser Begriff unbrauchbar, denn die Verstellung hätte keine Kriterien im Benehmen.
572. Liegt hier nicht etwas Ähnliches vor, wie das Verhältnis der euklidischen Geometrie zur Sinneserfahrung? (Ich meine: es sei eine tiefgehende Ähnlichkeit vorhanden.) Denn auch die euklidische Geometrie entspricht ja der Erfahrung nur in einer durchaus nicht leicht verständlichen Weise, und nicht etwa nur wie das Exaktere dem Unexakteren.
573. Es gibt doch im Benehmen Vertrauen und Mißtrauen!
Klagt einer z. B., so kann ich mit völliger Sicherheit vertrauensvoll reagieren, oder unsicher und wie einer, der Verdacht hat. Es braucht dazu keine Worte noch Gedanken.
574. Ist das, wovon er sagt, er habe es, und wovon ich sage, ich habe es, ohne daß wir dies aus irgendeiner Beobachtung erschließen,—ist es dasselbe, wie das, was wir aus der Beobachtung des Benehmens des Andern und aus seiner Überzeugungsäußerung entnehmen?
575. Kann man sagen: Ich schließe, daß er handeln wird, wie er zu handeln beabsichtigt?
(Fall der falschen Geste.)
576. Warum schließe ich nie von meinen Worten auf meine wahrscheinlichen Handlungen? Aus demselben Grunde, aus welchem ich nicht von meinem Gesichtsausdruck auf mein wahrscheinliches Benehmen schließe.—Denn nicht das ist das Interessante, daß ich nicht aus meinem Ausdruck der Gemütsbewegung auf meine Gemütsbewegung schließe, sondern, daß ich aus jenem Ausdruck auch nicht auf mein späteres Verhalten schließe, wie dies doch die Andern tun, die mich beobachten.
577. Willkürlich sind gewisse Bewegungen mit ihrer normalen Umgebung von Absicht, Lernen, Versuchen, Handeln. Bewegungen, von denen es Sinn hat zu sagen, sie seien manchmal willkürlich, manchmal unwillkürlich, sind Bewegungen in einer speziellen Umgebung
578. Wenn einer uns nun sagte, er esse unwillkürlich,—welche Evidenz würde mich dies glauben machen?
579. Man ruft sich ein Niesen oder einen Hustenanfall hervor, aber nicht eine willkürliche Bewegung. Und der Wille ruft das Niesen nicht hervor und auch nicht das Gehen.
580. Mein Ausdruck kam daher, daß ich mir das Wollen als ein Herbeiführen dachte,—aber nicht als ein Verursachen, sondern—ich möchte sagen—als ein direktes, nicht-kausales Herbeiführen. Und dieser Idee liegt die Vorstellung zu Grunde, daß der kausale Nexus die Verbindung zweier Maschinenteile durch einen Mechanismus, etwa eine Reihe von Zahnrädern ist.
581. Ist "Ich tue mein Möglichstes" die Äußerung eines Erlebnisses?—Ein Unterschied: Man sagt "Tue dein Möglichstes!"
582. Wenn einer mich auf der Straße trifft und fragt "Wohin gehst du?" und ich antworte "Ich weiß es nicht", so nimmt er an, ich habe keine bestimmte Absicht; nicht, ich wisse nicht, ob ich meine Absicht werde ausführen können. (Hebel.)
583. Was ist der Unterschied zwischen diesen beiden: Einer Linie unwillkürlich folgen——Einer Linie mit Absicht folgen.
Was ist der Unterschied zwischen diesen beiden: Eine Linie mit Bedacht und großer Aufmerksamkeit nachziehen——Aufmerksam beobachten, wie meine Hand einer Linie folgt.
584. Gewisse Unterschiede sind leicht anzugeben. Einer liegt im Voraussehen dessen, was die Hand tun wird.
585. Die Erfahrung: neue Erfahrung kennen zu lernen. Etwa beim Schreiben. Wann sagt man, man habe eine neue Erfahrung kennen gelernt? Wie gebraucht man so einen Satz?
586. Das Schreiben ist gewiß eine willkürliche Bewegung, und doch eine automatische. Und von einem Fühlen jeder Schreibbewegung ist natürlich nicht die Rede. Man fühlt etwas, aber könnte das Gefühl unmöglich zergliedern. Die Hand schreibt; sie schreibt nicht, weil man will, sondern man will, was sie schreibt.
Man sieht ihr nicht erstaunt oder mit Interesse beim Schreiben zu; denkt nicht "Was wird sie nun schreiben?" Aber nicht, weil man eben wünschte, sie solle das schreiben. Denn, daß sie schreibt, was ich wünsche, könnte mich ja erst recht in Erstaunen versetzen.
587. Das Kind lernt gehen, kriechen, spielen. Es lernt nicht, willkürlich und unwillkürlich spielen. Aber was macht die Bewegungen des Spiels zu willkürlichen Bewegungen?—Wie wäre es denn, wenn sie unwillkürlich wären?—Ich könnte ebensowohl fragen: Was macht denn diese Bewegung zu einem Spielen?—Ihr Charakter und ihre Umgebung.
588. Aktiv und passiv. Kann man es befehlen oder nicht? Dies scheint vielleicht eine weithergeholte Unterscheidung, ist es aber nicht. Es ist ähnlich wie: "Kann man sich (logische Möglichkeit) dazu entschließen oder nicht?"—Und das heißt: Wie ist es von Gedanken, Gefühlen etc. umgeben?
589. "Wenn ich mich anstrenge, tue ich doch etwas, habe doch nicht bloß eine Empfindung." Und so ist es auch; denn man befiehlt einem: "Streng dich an!" und er kann die Absicht äußern "Ich werde mich jetzt anstrengen". Und wenn er sagt "Ich kann nicht mehr!"—so heißt das nicht "Ich kann das Gefühl in meinen Gliedern—den Schmerz z. B.—nicht länger ertragen".—Andererseits aber leidet man unter der Anstrengung wie unter Schmerzen. "Ich bin gänzlich erschöpft"—wer das sagte, sich aber so frisch bewegte wie je, den würde man nicht verstehen.
590. Die Verbindung unseres Hauptproblems mit dem epistemologischen Problem des Wollens ist mir schon früher einmal aufgefallen. Wenn in der Psychologie ein solches hartnäckiges Problem auftritt, so ist es nie eine Frage nach der tatsächlichen Erfahrung (eine solche ist immer viel gutmütiger), sondern ein logisches, also eigentlich grammatisches Problem.
591. Mein Benehmen ist eben manchmal Gegenstand meiner Beobachtung, aber doch selten. Und das hängt damit zusammen, daß ich mein Benehmen beabsichtige. Selbst wenn der Schauspieler im Spiegel seine eigenen Mienen beobachtet, oder der Musiker genau auf jeden Ton seines Spiels merkt und ihn beurteilt, so geschieht es doch, um seine Handlung danach zu richten.
592. Was heißt es z. B., daß Selbstbeobachtung mein Handeln, meine Bewegungen unsicher macht?
Ich kann mich nicht unbeobachtet beobachten. Und ich beobachte mich nicht zu dem gleichen Zweck wie den Andern.
593. Wenn ein Kind im Zorn mit den Füßen stampft und heult,—wer würde sagen, es täte dies unwillkürlich? Und warum? Warum nimmt man an, es täte dies nicht unwillkürlich? Was sind die Zeichen des willkürlichen Handelns? Gibt es solche Zeichen?—Was sind denn die Zeichen der unwillkürlichen Bewegung? Sie folgt Befehlen nicht, wie die willkürliche Handlung. Es gibt ein "Komm her!", "Geh dort hin", "Mach diese Armbewegung!"; aber nicht "Laß dein Herz klopfen!"
594. Es gibt ein bestimmtes Zusammenspiel von Bewegungen, Worten, Mienen wie den Äußerungen des Unwillens oder der Bereitschaft, die die willkürlichen Bewegungen des normalen Menschen charakterisieren. Wenn man das Kind ruft, so kommt es nicht automatisch: Es gibt da z. B. die Gebärde "Ich will nicht!". Oder das freudige Kommen, den Entschluß zu kommen, das Fortlaufen mit dem Zeichen der Furcht, die Wirkungen des Zuredens, alle die Reaktionen des Spiels, die Zeichen des Überlegens und seine Wirkungen.
595. Wie könnte ich mir beweisen, daß ich meinen Arm willkürlich bewegen kann? Etwa, indem ich mir sage "Ich werde ihn jetzt bewegen" und er sich nun bewegt? Oder soll ich sagen "Einfach, indem ich ihn bewege"? Aber wie weiß ich, daß ich es getan habe, und er sich nicht nur durch Zufall bewegt hat? Fühle ich es am Ende doch? Und wie, wenn mich meine Erinnerung an frühere Gefühle täuschte, und es also gar nicht die richtigen maßgebenden Gefühle waren?! (Und welches sind die Richtigen?) Und wie weiß denn der Andere, ob ich den Arm willkürlich bewegt habe? Ich werde ihm vielleicht sagen "Befiehl mir, welche Bewegung du willst, und ich werde sie machen, um dich zu überzeugen".—Und was fühlst du denn in deinem Arm? "Nun, das Gewöhnliche." Es ist nichts Ungewöhnliches an den Gefühlen,—der Arm ist z. B. nicht gefühllos (wie wenn er 'eingeschlafen' wäre).
596. Eine Bewegung meines Körpers, von der ich nicht weiß, daß sie stattfindet oder stattgefunden hat, wird man unwillkürlich nennen.—Wie ist es aber, wenn ich bloß versuche, ein Gewicht zu heben, eine Bewegung also nicht stattfindet? Wie wäre es, wenn einer sich unwillkürlich anstrengte, ein Gewicht zu heben? Unter welchen Umständen würde man dies Verhalten 'unwillkürlich' nennen?
597. Kann nicht die Ruhe ebenso willkürlich sein, wie Bewegung? Kann das Unterlassen der Bewegung nicht willkürlich sein? Welch besseres Argument gegen ein Innervationsgefühl?
598. Was für ein merkwürdiger Begriff 'versuchen', 'trachten' ist; was man alles ‘zu tun trachten' kann! (Sich erinnern, ein Gewicht heben, aufmerken, an nichts denken.) Aber dann könnte man auch sagen: Was für ein merkwürdiger Begriff 'tun' ist! Welches sind die Verwandtschaftsbeziehungen zwischen 'Reden' und 'Denken', zwischen 'Reden' und 'zu sich selbst reden'? (Vergleiche die Verwandtschaftsbeziehungen zwischen den Zahlenarten.)
599. Man zieht ganz andere Schlüsse aus der unwillkürlichen Bewegung, als aus der willkürlichen: das charakterisiert die willkürliche Bewegung.
600. Aber wie weiß ich, daß diese Bewegung willkürlich war?—Ich weiß es nicht, ich äußere es.
601. "Ich ziehe so stark, wie ich kann." Wie weiß ich das? Sagt es mir mein Muskelgefühl? Die Worte sind ein Signal; und sie haben eine Funktion.
Aber erlebe ich denn nichts? Erlebe ich denn nicht etwas? Etwas Spezifisches? Ein spezifisches Gefühl der Anstrengung und des Nicht-weiter-könnens, des Anlangens an der Grenze? Freilich, aber diese Ausdrücke sagen nicht mehr, als "Ich ziche so stark, wie ich kann."
602. Vergleiche damit diesen Fall: Jemand soll sagen, was er fühlt, wenn ihm ein Gewicht auf der flachen Hand ruht. Ich kann mir nun vorstellen, daß hier ein Zwiespalt entsteht: Einerseits sagt er sich, was er fühle, sei eine Pressung gegen die Handfläche und eine Spannung in den Muskeln seines Arms; anderseits will er sagen: "aber das ist doch nicht alles; ich empfinde doch einen Zug, ein Streben des Gewichts nach unten!"—Empfindet er denn ein solches 'Streben'? Ja: wenn er nämlich an das 'Streben' denkt. Mit dem Wort "Streben" geht hier ein bestimmtes Bild, eine Geste, ein Tonfall; und in diesem siehst du das Erlebnis des Strebens.
(Denke auch daran: Manche Leute sagen, von dem und dem 'gehe ein Fluidum aus'.—Daher fiel uns auch das Wort "Einfluß" ein.)
603. Die Unvorhersehbarkeit des menschlichen Benehmens. Wäre sie nicht vorhanden,—würde man dann auch sagen, man könne nie wissen, was im Andern vorgeht?
604. Aber wie wär's, wenn das menschliche Benehmen nicht unvorhersehbar wäre? Wie hat man sich das vorzustellen? (D. h.: wie auszumalen, welche Verbindungen anzunehmen?)
605. Eine der philosophisch gefährlichsten Ideen ist, merkwürdigerweise, daß wir mit dem Kopf oder im Kopf denken.
606. Die Idee vom Denken als einem Vorgang im Kopf, in dem gänzlich abgeschlossenen Raum, gibt ihm etwas Okkultes.
607. Ist das Denken sozusagen ein spezifisch organischer Vorgang der Seele—gleichsam ein Kauen und Verdauen in der Seele? Kann man ihn dann durch einen anorganischen Vorgang ersetzen, der den gleichen Zweck erfüllt, sozusagen mit einer Prothese das Denken besorgen? Wie müßte man sich eine Denkprothese vorstellen?
608. Keine Annahme scheint mir natürlicher, als daß dem Assoziieren oder Denken kein Prozeß im Gehirn zugeordnet ist; so zwar, daß es also unmöglich wäre, aus Gehirnprozessen Denkprozesse abzulesen. Ich meine das so: Wenn ich rede oder schreibe, so geht, nehme ich an, ein meinem gesprochenen oder geschriebenen Gedanken zugeordnetes System von Impulsen von meinem Gehirn aus. Aber warum sollte das System sich weiter in zentraler Richtung fortsetzen? Warum soll nicht sozusagen diese Ordnung aus dem Chaos entspringen? Der Fall wäre ähnlich dem—daß sich gewisse Pflanzenarten durch Samen vermehrten so daß ein Same immer dieselbe Pflanzenart erzeugt, von der er erzeugt wurde,—daß aber nichts in dem Samen der Pflanze, die aus ihm wird, entspricht; so daß es unmöglich ist, aus den Eigenschaften oder der Struktur des Samens auf die der Pflanze, die aus ihm wird, zu schließen,—daß man dies nur aus seiner Geschichte tun kann. So könnte also aus etwas ganz Amorphem ein Organismus sozusagen ursachelos werden; und es ist kein Grund, warum sich dies nicht mit unserem Gedanken, also mit unserem Reden oder Schreiben etc. wirklich so verhalten sollte.
609. Es ist also wohl möglich, daß gewisse psychologische Phänomene physiologisch nicht untersucht werden können, weil ihnen physiologisch nichts entspricht.
610. Ich habe diesen Mann vor Jahren gesehen; nun sehe ich ihn wieder, erkenne ihn, erinnere mich seines Namens. Und warum muß es nun für dies Erinnern eine Ursache in meinem Nervensystem geben? Warum muß irgend etwas, was immer, in irgendeiner Form dort aufgespeichert worden sein? Warum muß er eine Spur hinterlassen haben? Warum soll es keine psychologische Gesetzmäßigkeit geben, der keine physiologische entspricht? Wenn das unsere Begriffe von der Kausalität umstößt, dann ist es Zeit, daß sie umgestoßen werden.
611. Das Vorurteil zugunsten des psycho-physischen Parallelismus ist cine Frucht primitiver Auffassungen unserer Begriffe. Denn wenn man Kausalität zwischen psychologischen Erscheinungen zuläßt, die nicht physiologisch vermittelt ist, so denkt man damit das Eingeständnis eines nebelhaften Seelenwesens zu machen.
612. Denke dir diese Erscheinung: Wenn ich will, daß jemand sich einen Text merkt, den ich ihm vorspreche, so daß er ihn mir später wiederholen kann, muß ich ihm ein Papier und einen Bleistift geben; und während ich spreche, schreibt er Striche, Zeichen auf das Papier; soll er später den Text reproduzieren, so folgt er jenen Strichen mit den Augen und sagt den Text her. Ich nehme aber an, seine Aufzeichnung sei keine Schrift, sie hänge nicht durch Regeln mit den Worten des Textes zusammen; und doch kann er ohne diese Aufzeichnung den Text nicht reproduzieren; und wird an ihr etwas geändert, wird sie zum Teil zerstört, so bleibt er beim 'Lesen' stecken oder spricht den Text unsicher oder unzuverlässig oder kann die Worte überhaupt nicht finden.—Das ließe sich doch denken!—Was ich die 'Aufzeichnung' nannte, wäre dann keine Wiedergabe des Textes, nicht eine Übersetzung sozusagen in einem anderen Symbolismus. Der Text wäre nicht in der Aufzeichnung niedergelegt. Und warum sollte er in unserm Nervensystem niedergelegt sein?
613. Warum soll nicht ein Naturgesetz einen Anfangs- und einen Endzustand eines Systems verbinden, den Zustand zwischen beiden aber übergehen? (Nur denke man nicht an Wirkung!)
614. "Wie kommt es, daß ich den Baum aufrecht sehe, auch wenn ich meinen Kopf zur Seite neige, und also das Netzhautbild das eines schiefstehenden Baums ist?" Wie kommt es also, daß ich den Baum auch unter diesen Umständen als einen aufrechten anspreche?—"Nun, ich bin mir der Neigung meines Kopfes bewußt, und ich bringe also die nötige Korrektur an der Auffassung meiner Gesichtseindrücke an."—Aber heißt das nicht, Primäres mit Sekundärem verwechseln? Denke dir, wir wüßten gar nichts von der innern Beschaffenheit des Auges,—würde dies Problem überhaupt auftauchen? Wir bringen ja hier in Wahrheit keine Korrekturen an, dies ist ja bloß eine Erklärung.
Wohl——aber da nun die Struktur des Auges einmal bekannt ist,—wie kommt es, daß wir so handeln, so reagieren? Aber muß es hier eine physiologische Erklärung geben? Wie, wenn wir sie auf sich beruhen ließen? Aber so würdest du doch nicht sprechen, wenn du das Verhalten einer Maschine prüftest!—Nun, wer sagt, daß in diesem Sinne das Lebewesen, der tierische Leib eine Maschine ist?—
615. (Ich habe noch nie eine Bemerkung darüber gelesen, daß, wenn man ein Auge schließt und "nur mit einem Auge sieht", man die Finsternis (Schwärze) nicht zugleich mit dem geschlossenen sieht.)
616. Die Grenzenlosigkeit des Gesichtsraumes ist am klarsten, wenn wir nichts sehen bei vollständiger Dunkelheit.
617. Wie verhält es sich mit dem Blinden; kann ihm ein Teil der Sprache nicht erklärt werden? Oder vielmehr nicht beschrieben werden?
618. Ein Blinder kann sagen, er sei blind und die Leute um ihn seien sehend. "Ja, aber meint er nicht doch etwas Anderes mit den Worten 'blind' und 'sehend' als der Sehende?" Worauf beruht es, daß man so etwas sagen will? Nun, wenn einer nicht wüßte, wie ein Leopard ausschaut, so könnte er doch sagen und verstehen "Dieser Ort ist sehr gefährlich, es gibt Leoparden dort". Man würde aber doch vielleicht sagen, er weiß nicht, was ein Leopard ist, also nicht oder nur unvollständig, was das Wort "Leopard" bedeutet, bis man ihm einmal ein solches Tier zeigt. Nun kommt es uns mit den Blinden ähnlich vor. Sie wissen sozusagen nicht, wie sehen ist.—Ist nun 'Furcht nicht kennen' analog dem 'nie einen Leoparden gesehen haben'? Das will ich natürlich verneinen.
619. Könnte ich denn nicht z. B. annehmen, daß er etwas Rotes sieht, wenn ich ihn auf den Kopf schlage? Es könnte das ja bei Sehenden einer Erfahrung entsprechen.
Das angenommen, so ist er doch für das praktische Leben blind. D. h., er reagiert nicht wie der normale Mensch. Wenn aber jemand mit den Augen blind wäre, dagegen sich so benähme, daß wir sagen müßten, er sieht mit den Handflächen (dieses Benehmen ist leicht auszumalen), so würden wir ihn als Sehenden behandeln und auch die Erklärung des Wortes 'rot' mit dem Täfelchen würden wir hier für möglich halten.
620. Du gibst jemandem ein Signal, wenn du dir etwas vorstellst; du benützt verschiedene Signale für verschiedene Vorstellungen.—Wie vereinbart ihr, was jedes Signal bedeuten soll?
621. Gehörsvorstellung, Gesichtsvorstellung, wie unterscheiden sie sich von den Empfindungen? Nicht durch "Lebhaftigkeit".
Vorstellungen belehren uns nicht über die Außenwelt, weder richtig noch falsch. (Vorstellungen sind nicht Halluzinationen, auch nicht Einbildungen.)
Während ich einen Gegenstand sehe, kann ich ihn mir nicht vorstellen.
Verschiedenheit der Sprachspiele: "Schau die Figur an!" und "Stell dir die Figur vor!"
Vorstellung dem Willen unterworfen.
Vorstellung nicht Bild. Welchen Gegenstand ich mir vorstelle, ersehe ich nicht aus der Ähnlichkeit des Vorstellungsbildes mit ihm.
Auf die Frage "Was stellst du dir vor", kann man mit einem Bild antworten.
622. Man möchte sagen: Der vorgestellte Klang sei in einem andern Raum als der gehörte. (Frage: Warum?) Das Gesehene in einem andern Raum, als das Vorgestellte.
Hören ist mit Hinhorchen verbunden; einen Klang sich vorstellen, nicht.
Darum ist der gehörte Klang in einem andern Raum als der vorgestellte.
623. Ich lese eine Geschichte und stelle mir während des Lesens, also während des aufmerksamen Schauens, also deutlichen Sehens, alles mögliche vor.
624. Es könnte Leute geben, die nie den Ausdruck gebrauchen "etwas vor dem inneren Auge sehen", oder einen ähnlichen; und diese könnten doch imstande sein, 'aus der Vorstellung', oder nach der Erinnerung zu zeichnen, zu modellieren, Andere nachzuahmen, etc. Ein solcher möge auch, ehe er etwas aus der Erinnerung zeichnet, die Augen schließen oder wie blind vor sich hinstarren. Und doch könnte er leugnen, daß er dann vor sich sieht, was später zeichnet. Aber wieviel müßte ich auf diese Äußerung geben? Ist nach ihr zu beurteilen, ob er eine Gesichtsvorstellung hat? (Nicht nur danach. Denk an den Ausdruck: "Jetzt sehe ich es vor mir—jetzt nicht mehr." Es gibt da eine echte Dauer.)
625. Ich hätte früher auch sagen können: Der Zusammenhang zwischen Vorstellen und Sehen ist eng; eine Ähnlichkeit aber gibt es nicht.
Die Sprachspiele, die diese Begriffe verwenden, sind grundverschieden,—hängen aber zusammen.
626. Unterschied: 'trachten, etwas zu sehen' und 'trachten, sich etwas vorzustellen'. Im ersten Fall sagt man etwa "Schau genau hin!", im zweiten "Schließ die Augen!"
627. Weil das Vorstellen eine Willenshandlung ist, unterrichtet es uns eben nicht über die Außenwelt.
628. Das Vorgestellte nicht im gleichen Raum wie das Gesehene. Sehen ist mit Schauen verbunden.
629. "Sehen und Vorstellen sind verschiedene Phänomene."—Die Wörter "sehen" und "vorstellen" haben verschieden Bedeutung! Ihre Bedeutungen beziehen sich auf eine Menge wichtiger Arten und Weisen menschlichen Verhaltens, auf Phänomene des menschlichen Lebens.
630. Sag dir wieder, wenn einer darauf besteht, was er "Gesichtsvorstellung" nennt, sei ähnlich dem Gesichtseindruck: daß er sich vielleicht irrt! Oder: Wie, wenn er sich darin irrte? Das heißt: Was weißt du von der Ähnlichkeit seines Gesichtseindrucks und seiner Gesichtsvorstellung?! (Ich rede vom Andern, weil, was von ihm gilt, auch von mir gilt.)
Was weißt du also von dieser Ähnlichkeit? Sie äußert sich nur in den Ausdrücken, die er zu gebrauchen geneigt ist; nicht in dem, was er mit diesen Ausdrücken sagt.
631. "Es ist gar kein Zweifel: die Gesichtsvorstellung und der Gesichtseindruck sind von derselben Art!" Das mußt du aus deiner eigenen Erfahrung wissen, und dann ist es also etwas, was für dich stimmen mag und für andere nicht. (Und das gilt natürlich auch für mich, wenn ich es sage.)
632. Wenn wir uns etwas vorstellen, beobachten wir nicht. Daß die Bilder kommen und vergehen, geschieht uns nicht. Wir sind nicht überrascht von diesen Bildern und sagen "Sieh da!..." (Gegensatz z. B. zu den Nachbildern.)
633. Wir 'verscheuchen' nicht Gesichtseindrücke, aber Vorstellungen. Und wir sagen von jenen auch nicht, wir könnten sie nicht verscheuchen.
634. Wenn Einer wirklich sagte "Ich weiß nicht, sehe ich jetzt einen Baum, oder stelle ich mir einen vor", so würde ich zunächst glauben, er meine: "oder bilde ich mir nur ein, es stehe dort einer". Meint er das nicht, so könnte ich ihn überhaupt nicht verstehen—wollte mir aber jemand diesen Fall erklären und sagte "Er hat eben so außergewöhnlich lebhafte Vorstellungen, daß er sie für Sinneseindrücke halten kann"—verstünde ich es jetzt?
635. Muß man aber hier unterscheiden: (a) mir das Gesicht eines Freundes z. B. vorstellen, aber nicht in dem Raum, der mich umgibt—(b) mir an dieser Wand dort ein Bild vorstellen?
Man könnte auf die Aufforderung "Stell dir dort drüben einen runden Fleck vor" sich einbilden, wirklich einen dort zu sehen.
636. Das 'Vorstellungsbild' tritt nicht dort ins Sprachspiel ein, wo man es vermuten möchte.
637. Ich lerne den Begriff 'sehen' mit dem Beschreiben dessen, was ich sehe. Ich lerne beobachten und das Beobachtete beschreiben. Ich lerne den Begriff 'vorstellen' in einer andern Verbindung. Die Beschreibungen des Gesehenen und des Vorgestellten sind allerdings von derselben Art, und eine Beschreibung könnte sowohl das Eine wie auch das Andere sein; aber sonst sind die Begriffe durchaus verschieden. Der Begriff des Vorstellens ist eher wie der eines Tuns, als eines Empfangens. Das Vorstellen könnte man einen schöpferischen Akt nennen. (Und nennt es ja auch so.)
638. "Ja, aber die Vorstellung selbst, so wie der Gesichtseindruck ist doch das innere Bild, und du redest nur von den Verschiedenheiten der Erzeugung, Entstehung. Behandlung des Bildes." Die Vorstellung ist nicht ein Bild, noch ist der Gesichtseindruck eines. Weder 'Vorstellung' noch 'Eindruck' ist ein Bildbegriff, obwohl in beiden Fällen ein Zusammenhang mit einem Bild statt hat, und jedes Mal ein anderer.
639. Was nennst du "Erlebnisinhalt" des Sehens, was "Erlebnisinhalt" der Vorstellung?
640. "Aber könnte ich mir nicht einen Erlebnisinhalt denken von der Art der visuellen Vorstellung, aber dem Willen nicht unterworfen, in dieser Beziehung also wie der Gesichtseindruck?"
641. (Daß man nämlich die Willenshandlung des Vorstellens nicht mit der Bewegung des Körpers vergleichen kann, ist klar; denn, ob die Bewegung stattgefunden hat, das zu beurteilen sind auch Andere befähigt; während es bei der Bewegung meiner Vorstellungen immer nur darauf ankäme, was ich zu sehen behaupte, was immer irgend ein Anderer sieht. Es würden also die sich bewegenden wirklichen Gegenstände aus der Betrachtung herausfallen, da es auf sie gar nicht ankäme.)
642. Sagte man also: "Vorstellungen sind innere Bilder, ähnlich oder ganz so wie meine Gesichtseindrücke, nur meinem Willen untertan"—so hätte das vorerst noch keinen Sinn.
Denn wenn einer zu berichten gelernt hat, was er dort sieht, oder was ihm dort zu sein scheint, so ist es doch nicht klar, was der Befehl bedeute, er solle jetzt das dort sehen, oder es solle ihm jetzt das dort zu sein scheinen.
643. "Durch den bloßen Willen bewegen", was heißt es? Etwa, daß die Vorstellungsbilder meinem Willen immer genau folgen, während meine zeichnende Hand, mein Bleistift, das nicht tut? Immerhin wäre es ja dann doch möglich zu sagen: "Für gewöhnlich stelle ich mir ganz genau vor, was ich will; heute ist es anders ausgefallen." Gibt es denn ein 'Mißlingen der Vorstellung'?
644. Ein Sprachspiel umfaßt ja den Gebrauch mehrerer Wörter.
645. Nichts könnte falscher sein als zu sagen, Sehen und Vorstellen seien verschiedene Tätigkeiten. Das ist, als sagte man im Schach ziehen und verlieren seien verschiedene Tätigkeiten.
646. Wenn wir als Kinder die Worte "sehen", "schauen", "vorstellen" gebrauchen lernen, so spielen bei dieser Abrichtung Willenshandlungen und Befehle eine Rolle. Aber für jedes der drei Wörter eine Andere. Das Sprachspiel "Schaul" und "Stell dir .... vor!"—Wie soll ich sie nur vergleichen?—Wenn wir jemanden abrichten wollen, daß er auf den Befehl "Schau ....!" reagiert, und dazu, daß er den Befehl "Stell dir .... vor!" versteht, so müssen wir ihn doch offenbar ganz Anderes lehren. Reaktionen, die zu diesem Sprachspiel gehören, gehören zu jenem nicht. Ja, ein enger Zusammenhang der Sprachspiele ist natürlich da, aber eine Ähnlichkeit?—Stücke des einen sind Stücken des andern ähnlich, aber die ähnlichen Stücke sind nicht homolog.
647. Ich könnte mir etwas Ähnliches für wirkliche Spiele denken.
648. Ein Sprachspiel analog einem Teil eines andern. Ein Raum in begrenzte Stücke eines Raums projiziert. Ein 'löchriger' Raum. (Zu "Innen und Aussen".)
649. Denken wir uns eine Variante des Tennisspiels: es wird in die Regeln dieses Spiels die aufgenommen, der Spieler habe sich bei gewissen Spielhandlungen das und das vorzustellen! (Der Zweck dieser Regel sei, das Spiel zu erschweren.) Der erste Einwand ist: man könne in diesem Spiel zu leicht schwindeln. Aber dem wird mit der Annahme begegnet, das Spiel werde nur von ehrlichen und zuverlässigen Menschen gespielt. Hier haben wir also ein Spiel mit innern Spielhandlungen.—
Welcher Art ist nun die innere Spielhandlung, worin besteht sie? Darin, daß er—der Spielregel gemäß—sich ..... vorstellt.—Könnte man aber nicht auch sagen: Wir wissen nicht, welcher Art die innere Spielhandlung ist, die er der Regel gemäß ausführt; wir kennen nur ihre Äußerungen? Die innere Spielhandlung sei ein X, dessen Natur wir nicht kennen. Oder: Es gebe auch hier nur äußere Spielhandlungen: die Mitteilung der Spielregel und das, was man die 'Äußerung des innern Vorgangs' nennt.——Nun, kann man das Spiel nicht auf alle drei Arten beschreiben? Auch das mit dem 'unbekannten' X ist eine ganz mögliche Beschreibungsart. Der eine sagt, die sogenannte 'innere' Spielhandlung sei mit einer Spielhandlung im gewöhnlichen Sinne nicht vergleichbar—der Andre sagt, sie sei mit einer solchen vergleichbar—der Dritte: sie sci vergleichbar nur mit einer Handlung, die im Geheimen geschieht, und die niemand kennt, als der Handelnde.
Wichtig ist für uns, daß wir die Gefahren des Ausdrucks "innere Spielhandlung" sehen. Er ist gefährlich, weil er Verwirrung anrichtet.
650. Erinnerung: "Ich sehe uns noch an jenem Tisch sitzen".—Aber habe ich wirklich das gleiche Gesichtsbild—oder eines von denen, welche ich damals hatte? Sehe ich auch gewiß den Tisch und meinen Freund vom gleichen Gesichtspunkt wie damals, also mich selbst nicht?——Mein Erinnerungsbild ist nicht Evidenz jener vergangenen Situation; wie eine Photographie es wäre, die, damals aufgenommen, mir jetzt bezeugt, daß es damals so war. Das Erinnerungsbild und die Erinnerungsworte stehen auf gleicher Stufe.
651. Das Achselzucken, Kopfschütteln, Nicken u.s.f. nennen wir Zeichen vor allem darum, weil sie in dem Gebrauch unsrer Wortsprache eingebettet sind.
652. Wenn man es für selbstverständlich hält, daß der Mensch sich an seiner Phantasie vergnügt, so bedenke man, daß die Phantasie nicht einem gemalten Bild, einer Plastik oder einem Film entspricht, sondern einem komplexen Gebilde aus heterogenen Bestandteilen—Zeichen und Bildern.
653. Manche Menschen erinnern sich an ein musikalisches Thema in der Weise, daß das Notenbild vor ihnen auftaucht, und sie es herunterlesen.
Es wäre denkbar, daß, was wir "Erinnern" bei einem Menschen nennen, darin bestünde, daß er sich im Geiste ein Buch nachschlagen sähe, und das, was er in diesem Buch liest, eben das Erinnerte wäre. (Wie reagiere ich auf eine Erinnerung?)
654. Kann man ein Erinnerungserlebnis beschreiben?—Gewiß.—Aber kann man das Erinnerungshafte an diesem Erlebnis beschreiben? Was heißt das? (Das unbeschreibliche Aroma.)
655. "Ein Bild (Vorstellungsbild, Erinnerungsbild) der Sehnsucht". Man denkt, man habe schon alles damit getan, daß man von einem 'Bild' redet; denn die Sehnsucht ist eben ein Bewußtseinsinhalt, und dessen Bild ist etwas, was ihm (sehr) ähnlich ist, wenn auch undeutlicher als das Original.
Und man könnte ja wohl von einem, der die Sehnsucht auf dem Theater spielt, sagen, er erlebe oder habe ein Bild der Sehnsucht: nämlich nicht als Erklärung seines Handelns, sondern zu dessen Beschreibung.
656. Sich eines Gedankens schämen. Schämt man sich dessen, daß man den und den Satz zu sich selbst in der Vorstellung gesprochen hat?
Die Sprache hat eben eine vielfache Wurzel; sie hat Wurzeln, nicht eine Wurzel. [Randbemerkung: ((Sich eines Gedankens, einer Absicht erinnern.)) Keim.]
657. "Es schmeckt genau wie Zucker". Wie kommt es, daß ich dessen so sicher sein kann?—Und zwar auch, wenn es sich dann als falsch herausstellt. Und was erstaunt mich daran? Daß ich den Begriff Zucker in eine so feste Verbindung mit der Geschmacksempfindung bringe. Daß ich die Substanz Zucker direkt im Geschmack zu erkennen scheine.
Aber statt des Ausdrucks "Es schmeckt genau ...." könnte ich ja primitiver "Zucker!" ausrufen. Und kann man denn sagen, bei dem Wort 'schwebe mir die Substanz Zucker vor'? Wie tut sie das?
658. Kann ich sagen, dieser Geschmack brächte gebieterisch den Namen "Zucker" mit sich; oder aber das Bild eines Stücks Zucker? Keines von beiden scheint richtig. Ja, gebieterisch ist das Verlangen nach dem Begriff 'Zucker' allerdings und zwar ebenso, wie nach dem Begriff 'rot', wenn wir ihn zur Beschreibung des Gesehenen verwenden.
659. Ich erinnere mich, daß Zucker so geschmeckt hat. Es kommt mir das Erlebnis zurück ins Bewußtsein. Aber freilich: wie weiß ich, daß es das frühere Erlebnis ist? Das Gedächtnis hilft mir da nicht mehr. Nein, diese Worte,—das Erlebnis komme zurück ....,—sind nur eine Umschreibung, keine Beschreibung des Erinnerns.
Aber wenn ich sage "Es schmeckt genau wie Zucker", so findet in einem wichtigen Sinne gar kein Erinnern statt. Ich begründe also mein Urteil oder meinen Ausruf nicht. Wer mich fragt, "Was meinst du mit 'Zucker'?"—dem werde ich allerdings ein Stück Zucker zu zeigen trachten. Und wer fragt "Wie weißt du, daß Zucker so schmeckt", werde ich allerdings antworten "ich habe tausende Male Zucker gegessen"—aber das ist nicht eine Rechtfertigung, die ich mir selbst gebe.
660. "Es schmeckt wie Zucker." Man erinnert sich genau und mit Sicherheit, wie Zucker schmeckt. Ich sage nicht "Ich glaube, so schmeckt Zucker". Welch merkwürdiges Phänomen! Eben das Phänomen des Gedächtnisses.—Aber ist es richtig, es ein merkwürdiges Phänomen zu nennen?
Es ist ja nichts weniger als merkwürdig. Jene Sicherheit ist ja nicht (um ein Haar) merkwürdiger, als es die Unsicherheit wäre. Was ist denn merkwürdig? Das, daß ich mit Sicherheit sage "Das schmeckt wie Zucker"? oder, daß es dann wirklich Zucker ist? Oder, daß andere dasselbe finden?
Wenn das sichere Erkennen des Zuckers merkwürdig ist, so wäre es also das Nichterkennen weniger.
661. "Welcher seltsame und furchtbare Laut. Ich werde ihn nie vergessen." Und warum sollte man das nicht vom Erinnern sagen können ("Welche seltsame .... Erfahrung ...."), wenn man zum ersten Mal in die Vergangenheit gesehen hat?—
662. Erinnern: ein Sehen in die Vergangenheit. Träumen könnte man so nennen, wenn es uns Vergangenes vorführt. Nicht aber Erinnern; denn auch wenn es uns Szenen mit halluzinatorischer Klarheit zeigte, so lehrt es uns nun doch erst, daß dies das Vergangene sei.
663. Aber wenn uns nun das Gedächtnis die Vergangenheit zeigt, wie zeigt es uns, daß es die Vergangenheit ist?
Es zeigt uns eben nicht die Vergangenheit. So wenig, wie unsere Sinne die Gegenwart.
664. Man kann auch nicht sagen, sie teile uns die Vergangenheit mit. Denn selbst, wäre das Gedächtnis eine hörbare Stimme, die zu uns spräche,—wie könnten wir sie verstehen? Sagt sie uns z. B. "Gestern war schönes Wetter", wie kann ich lernen, was "gestern" bedeutet?
665. Ich führe mir selbst nur so etwas vor, wie ich es auch den Andern vorführe.
666. Ich kann dem Andern mein gutes Gedächtnis vorführen, und auch mir selbst vorführen. Ich kann mich selbst ausfragen. (Vokabeln, Daten.)
667. Aber wie führe ich mir das Erinnern vor? Nun, ich frage mich "Wie verbrachte ich den heutigen Morgen?" und antworte mir darauf.—Aber was habe ich mir nun eigentlich vorgeführt? War es das Erinnern? Nämlich, wie das ist, sich an etwas zu erinnern?—Hätte ich denn damit einem Andern das Erinnern vorgeführt?
668. Die Bedeutung eines Wortes vergessen—sich wieder an sie erinnern. Was für Vorgänge gibt es da? An was erinnert man sich, was fällt einem da ein, wenn man sich wieder daran erinnert, was das englische Wort "perhaps" bedeutet.
669. Wenn man mich fragt: "Weißt du das ABC?" und ich antworte mit "ja", so sage ich doch nicht, daß ich jetzt im Geist das ABC durchgehe, oder in einem besondern Gemütszustand bin, der irgendwie dem Hersagen des ABC äquivalent ist.
670. Man kann doch einen Spiegel besitzen; besitzt man dann auch das Spiegelbild, das sich in ihm zeigt?
671. Etwas sagen, ist eine Tätigkeit, geneigt sein, etwas zu sagen, ein Zustand. "Aber warum besteht der?"—Gib dir darüber Rechenschaft, wie der Ausdruck verwendet wird!
672. "Solange die Temperatur des Stabes nicht unter ..... herabsinkt, kann man ihn schmieden." Es hat also Sinn zu sagen: "ich kann ihn von 5 bis 6 Uhr schmieden". Oder: "Ich kann von 5 bis 6 Schach spielen", d. h., ich habe von 5 bis 6 Zeit.—"Solange mein Puls nicht unter .... herabsinkt, kann ich die Rechnung ausführen." Diese Rechnung braucht 1½ Minuten; wielange braucht es aber: sie ausführen können? Und wenn du sie eine Stunde lang rechnen kannst, fängst du da immer wieder von Frischem an?
673. Die Aufmerksamkeit ist dynamisch, nicht statisch—möchte man sagen. Ich vergleiche das Aufmerken zuerst mit einem Hinstarren: das ist es aber nicht, was ich Aufmerksamkeit nenne; und will nun sagen, ich finde, man könne nicht statisch aufmerken.
674. Wenn ich in einem bestimmten Falle sage: die Aufmerksamkeit besteht in der Bereitschaft, jeder kleinsten Bewegung, die sich zeigen mag, zu folgen,—so siehst du schon, daß die Aufmerksamkeit nicht das starre Hinschauen ist, sondern ein Begriff anderer Art.
675. Zustände: 'Einen Berg ersteigen können', kann man einen Zustand meines Körpers nennen. Ich sage: "Ich kann hinaufsteigen—ich meine: ich bin stark genug dazu". Vergleiche damit diesen Zustand des Könnens: "Ja, ich kann dorthin gehen—ich meine: ich habe Zeit dazu."
676. Welche Rolle spielen falsche Sätze in einem Sprachspiel? Ich glaube, es gibt verschiedene Fälle.
(1) Einer hat die Signallaternen an einer Straßenkreuzung zu beobachten, und einem Andern zu sagen, welche Farben sie zeigen. Er verspricht sich dabei und sagt die falsche Farbe.
(2) Es werden meteorologische Beobachtungen angestellt und nach gewissen Regeln aus ihnen das Wetter für den nächsten Tag vorhergesagt. Die Vorhersage trifft ein oder nicht.
Im ersten Fall kann man sagen, er spielt falsch; im zweiten nicht—wie ich seinerzeit glaubte.
Man wird hier (nämlich) von einer Frage geplagt, die etwa so lautet: Gehört die Verifikation noch (mit) zum Sprachspiel?
677. Ich behaupte: "Wenn dies eintrifft, so wird das eintreffen. Habe ich darin Recht, so zahlst du mir einen Schilling, habe ich Unrecht, so zahle ich dir einen, bleibt es unentschieden, so zahlt keiner." Das könnte man auch so ausdrücken: Der Fall, in welchem die Prämisse nicht eintrifft, interessiert uns nicht, wir reden nicht von ihm. Oder auch: es ist uns hier nicht natürlich, die Wörter "ja" und "nein" so zu gebrauchen, wie in dem Fall (und solche Fälle gibt es), in welchem uns die materielle Implikation interessiert. Mit "Nein" wollen wir hier sagen "p und nicht q", mit "Ja" nur "p und q". Es gibt keinen Satz vom ausgeschlossenen Dritten, der so lautet: Du gewinnst die Wette oder verlierst sie—ein Drittes gibt es nicht.
678. Einer wirft im Würfelspiel etwa 5, dann 4 und sagt "Hatte ich bloß statt der seine 4 geworfen, so hätte ich gewonnen"! Die Bedingtheit ist nicht physikalisch sondern nur mathematisch, denn man könnte antworten: "Hättest du zuerst 4 geworfen,—wer weiß, was du danach geworfen hättest!"
679. Sagst du nun "Die Verwendung des Konjunktivs beruht auf dem Glauben an ein Naturgesetz"—so kann man entgegnen: "Sie beruht nicht auf diesem Glauben; sie und dieser Glaube stehen auf gleicher Stufe." (Ich hörte im Film einen Vater zu seiner Tochter sagen, er hätte eine Andre zur Frau nehmen sollen: "Sie hätte deine Mutter sein sollen"! Warum ist das unrichtig?)
680. Das Schicksal steht im Gegensatz zum Naturgesetz. Das Naturgesetz will man ergründen und verwenden, das Schicksal nicht.
681. "Wenn p eintrifft, so trifft q ein" könnte man eine bedingte Vorhersage nennen. D. h.: für den Fall nicht-p mache ich keine Vorhersage. Aber darum wird, was ich sage, durch "nicht- und nicht-q" auch nicht wahrgemacht.
Oder auch so: es gibt bedingte Vorhersagen, und "p impliziert q" ist keine solche.
682. Den Satz "Wenn p eintrifft, so trifft q ein", will ich "S" nennen.—"S oder nicht-S" ist eine Tautologie: aber ist es (auch) der Satz vom ausgeschlossenen Dritten? Oder auch so: Wenn ich sagen will, daß die Vorhersage "S" richtig, falsch oder unentschieden sein kann, wird das durch den Satz ausgedrückt "nicht (S oder nicht-S)"?
683. Ist die Verneinung eines Satzes identisch mit der Disjunktion der nicht ausgeschlossenen Fälle? Sie ist es in manchen Fällen. (Z. B. in diesem: "Die Permutation der Elemente A B C, die er anschrieb, war nicht A C B.")
684. Der wichtige Sinn des Fregeschen Behauptungszeichens wird vielleicht am besten dadurch gefaßt, daß wir sagen: es bezeichnet deutlich den Anfang des Satzes.—Das ist wichtig: denn unsere philosophischen Schwierigkeiten, das Wesen der 'Negation' und des 'Denkens' betreffend, hängen damit zusammen, daß ein Satz "
685. Ein Widerspruch verhindert mich, im Sprachspiel zur Tat zu kommen.
686. Nehmen wir aber an, das Sprachspiel bestünde eben darin, mich fortwährend von einem Entschluß in den entgegengesetzten zu werfen!
687. Der Widerspruch ist nicht als Katastrophe aufzufassen, sondern als eine Mauer, die uns anzeigt, daß wir hier nicht weiter können.
688. Ich möchte nicht so sehr fragen "Was müssen wir tun, um einen Widerspruch zu vermeiden?", als "Was sollen wir tun, wenn wir zu einem Widerspruch gelangt sind?"
689. Warum ist ein Widerspruch mehr zu fürchten als eine Tautologie?
690. Unser Motto könnte sein: "Lassen wir uns nicht behexen!"
691. "Der Kretische Lügner". Statt zu sagen "ich lüge", könnte er auch hinschreiben "dieser Satz ist falsch". Die Antwort darauf wäre: "Wohl, aber welchen Satz meinst du?"—"Nun, diesen Satz."—"Ich verstehe, aber von welchem Satz ist in ihm die Rede?"—"Von diesem."—"Gut, und auf welchen Satz spielt dieser an?" u.s.w. Er könnte uns so nicht erklären, was er meint, ehe er zu einem kompletten Satz übergeht.—Man kann auch sagen: Der fundamentale Fehler liegt darin, daß man denkt, ein Wort, z. B. "dieser Satz", könne auf seinen Gegenstand gleichsam anspielen (aus der Entfernung hindeuten), ohne ihn vertreten zu müssen.
692. Stellen wir uns die Frage: Welchem praktischen Zweck kann Russell's Theorie der Typen dienen?—R. macht uns darauf aufmerksam, daß wir manchmal den Ausdruck der Allgemeinheit einschränken müssen um zu vermeiden, daß unerwünschte Konsequenzen aus ihm gezogen werden.
693. Das Raisonnement, das zu einem endlosen Regreß führt, ist nicht darum aufzugeben, 'weil wir so nie das Ziel erreichen können', sondern, weil es hier ein Ziel nicht gibt; so daß es gar keinen Sinn hat zu sagen "wir können es nicht erreichen".
Wir meinen leicht, wir müßten den Regreß ein paar Stufen weit durchlaufen und ihn dann sozusagen in Verzweiflung aufgeben. Während seine Ziellosigkeit (das Fehlen des Zieles im Kalkül) aus der Anfangsposition zu entnehmen ist.
694. Eine Variante des Cantor'schen Diagonalbeweises: N = F(k, n) sei die Form der Gesetze für die Entwicklung von Dezimalbrüchen. N ist die n-te Dezimalstelle der k-ten Entwicklung. Das Gesetz der Diagonale ist dann: N = F (n, n) = Def. F'(n).
Zu beweisen ist, daß F'(n) nicht eine der Regeln F (k, n) sein kann. Angenommen, es sei die 100ste. Dann lautet die Regel zur Bildung
- von F'(1)F(1,1)
- von F'(2)F(2,2) etc.
aber die Regel zur Bildung der 100sten Stelle von F'(n) wird F(100,100); d. h., sie sagt uns nur, daß die 100ste Stelle sich selber gleich sein soll, ist also für n = 100 keine Regel.
Die Spielregel lautet "Tu das Gleiche, wie ....!"—und im besondern Fall wird sie nun "Tu das Gleiche, wie das, was du tust!"
695. Das Verstehen der mathematischen Frage. Wie wissen wir, ob wir eine mathematische Frage verstehen?
Eine Frage—kann man sagen—ist ein Auftrag. Und einen Auftrag verstehen, heißt: wissen, was man zu tun hat. Ein Auftrag kann natürlich ganz vag sein—z. B., wenn ich sage: "Bring ihm etwas, was ihm gut tut!" Aber dies kann heißen: denk an ihn, seinen Zustand etc. in freundlicher Weise und dann bring ihm etwas, was deiner Gesinnung gegen ihn entspricht.
696. Die mathematische Frage ist eine Herausforderung. Und man könnte sagen: sie hat Sinn, wenn sie uns zu einer mathematischen Tätigkeit anspornt.
697. Man könnte dann auch sagen, eine Frage in der Mathematik habe Sinn, wenn sie die mathematische Phantasie anregt.
698. Übersetzen von einer Sprache in die andere, ist eine mathematische Aufgabe, und das Übersetzen eines lyrischen Gedichts z. B. in eine fremde Sprache ist ganz analog einem mathematischen Problem. Denn man kann wohl das Problem stellen "Wie ist dieser Witz (z. B.) durch einen Witz in der andern Sprache zu übersetzen?", d. h. zu ersetzen; und das Problem kann auch gelöst sein; aber eine Methode, ein System zu seiner Lösung gab es nicht.
699. Denk die Menschen, die mit 'äußerst komplizierten' Zahlzeichen rechnen. Diese stellen sich aber dar als Figuren, welche entstehen, wenn man unsere Zahlzeichen aufeinander schreibt.
Sie schreiben z. B. π bis zur fünften Stelle so:  Wer ihnen zusähe, fände es schwer zu erraten, was sie tun. Und sie könnten es vielleicht selbst nicht erklären. Es kann ja dieses Zahlzeichen, in etwas anderer Schrift geschrieben, seine Erscheinung (für uns) zur Unkenntlichkeit ändern. Und was die Leute täten, erschiene uns rein intuitiv.
Wer ihnen zusähe, fände es schwer zu erraten, was sie tun. Und sie könnten es vielleicht selbst nicht erklären. Es kann ja dieses Zahlzeichen, in etwas anderer Schrift geschrieben, seine Erscheinung (für uns) zur Unkenntlichkeit ändern. Und was die Leute täten, erschiene uns rein intuitiv.
700. Warum zählen wir? Hat es sich als praktisch erwiesen? Haben wir unsere Begriffe, z. B. die psychologischen, weil es sich als vorteilhaft erwiesen hat?—Und doch haben wir gewisse Begriffe eben deswegen, haben sie deswegen eingeführt.
701. Übrigens tritt der Unterschied zwischen dem, was man Sätze der Mathematik nennt und Erfahrungssätzen zu Tage, wenn man bedenkt, ob es Sinn hat zu sagen: "ich wünschte, 2 × 2 wäre 5!"
702. Wenn man bedenkt, daß die Gleichung 2 + 2 = 4 ein Beweis des Satzes ist "es gibt gerade Zahlen", so sieht man, wie lose hier das Wort "Beweis" gebraucht ist. Aus der Gleichung 2 + 2 = 4 soll der Satz "es gibt gerade Zahlen" hervorgehen?!—Und was ist der Beweis der Existenz von Primzahlen?—Die Methode der Zerlegung in Primfaktoren. Aber in dieser Methode wird ja überhaupt nicht geredet, auch nicht von 'Primzahlen'.
703. "Die Kinder müßten, um das Rechnen der Volksschule zu verstehen, bedeutende Philosophen sein; in Ermanglung dessen brauchen sie die Übung."
704. Russell und Frege fassen den Begriff gleichsam als Eigenschaft eines Dings auf. Aber es ist sehr unnatürlich, die Worte "Mensch", "Baum", "Abhandlung", "Kreis" als Eigenschaften eines Substrats aufzufassen.
705. Die Dirichlet'sche Auffassung der Funktion ist nur dort möglich, wo sie nicht ein unendliches Gesetz durch eine Liste ausdrücken will, denn eine unendliche Liste gibt es nicht.
706. Die Zahlen sind der Mathematik nicht fundamental.
707. Der Begriff des 'Ordnens' der Rationalzahlen z. B. und der 'Unmöglichkeit', die Irrationalzahlen so zu ordnen. Vergleiche das mit dem, was man 'Ordnen' von Ziffern nennt. Gleichermaßen der Unterschied zwischen dem 'Zuordnen' einer Ziffer (oder Nuß) zu einer andern und dem 'Zuordnen' aller ganzen Zahlen zu den geraden Zahlen; etc. Überall Begriffsverschiebungen.
708. Es gibt offenbar eine Methode, ein gerades Lineal anzufertigen. Diese Methode schließt ein Ideal ein, ich meine, ein Näherungsverfahren mit unbegrenzter Möglichkeit, denn eben dieses Verfahren ist das Ideal.
Oder vielmehr: Nur, wenn es ein Näherungsverfahren mit unbegrenzter Möglichkeit ist, kann (nicht muß) die Geometrie dieses Verfahrens die euklidische sein.
709. Die Rechnung als Ornament zu betrachten, das ist auch Formalismus, aber einer guten Art.
710. Man kann die Rechnung als Ornament betrachten. Eine Figur in der Ebene kann an eine andere passen oder nicht, mit anderen in verschiedener Weise zusammengefaßt werden. Wenn die Figur noch gefärbt ist, so gibt es dann noch ein Passen. (Die Farbe ist nur eine weitere Dimension.)
711. Es gibt eine Betrachtungsweise der elektrischen Maschinen und Apparate (Dynamos, Radiostationen, etc., etc.), die sozusagen ohne vorgefaßtes Verständnis diese Gegenstände als eine Verteilung von Kupfer, Eisen, Gummi, etc. im Raum ansieht. Und diese Betrachtungsweise könnte zu manchem interessanten Resultat führen. Sie ist ganz analog der eines mathematischen Satzes als Ornament.—Es ist natürlich eine durchaus strenge und korrekte Auffassung; und das Charakteristische und Schwierige an ihr ist, daß sie den Gegenstand ohne jede vorgefaßte Idee betrachtet (sozusagen von einem Marsstandpunkt), oder vielleicht richtiger: die normale vorgefaßte Idee zerstört (durchkreuzt).
712. (Der Stil meiner Sätze ist außerordentlich stark von Frege beeinflußt. Und wenn ich wollte, so könnte ich wohl diesen Einfluß feststellen, wo ihn auf den ersten Blick keiner sähe.)
713. "Leg es hier hin"—wobei ich mit dem Finger den Platz bezeichne—dies ist eine absolute Ortsangabe. Und wer sagt, der Raum sei absolut, möchte als Argument dafür vorbringen: "Es gibt doch einen Ort: Hier." [Randbemerkung: ((Vielleicht zu den ersten Sprachspielen.))]
714. Man könnte sich eine Geisteskrankheit denken, in welcher Einer Namen nur in Anwesenheit ihrer Träger gebrauchen und verstehen kann.
715. Es könnte von Zeichen ein Gebrauch gemacht werden solcher Art, daß die Zeichen nutzlos würden (daß man sie viel leicht vernichtete), sobald der Träger aufhörte zu existieren.
In diesem Sprachspiel hat sozusagen der Name den Gegenstand an einer Schnur; und hört der Gegenstand auf zu existieren, so kann man den Namen, der mit ihm zusammen gearbeitet hat, wegwerfen. (Das Wort "handle" für den Eigennamen.)
716. Wie ist es mit den beiden Sätzen: "dieses Blatt ist rot" und "dieses Blatt hat die Farbe, die auf Deutsch 'rot' heißt"? Sagen beide dasselbe?
Hängt das nicht davon ab, was das Kriterium dafür ist, daß eine Farbe auf Deutsch 'rot' heißt?
717. "Gott kannst du nicht mit einem Andern reden hören, sondern nur, wenn du der Angeredete bist."—Das ist eine grammatische Bemerkung.
- ↑ Im Original findet man keine Zeichnung: der Leser möge sich etwas Passendes ausdenken. Es gibt verschiedene Möglichkeiten; wir haben eine Zeichnung von A2569875 (CC BY-SA) benutzt. Herausgeber der digitalen Ausgabe.
- ↑ Vermutung der Herausgeber der Papierausgabe.
- ↑ Freud spricht von seiner 'dynamischen' Theorie des Traums.
